Загальноосвітня школа І-ІІІ ступенів с. Добре

 

 

 

 

 

 

 

 

Конспект уроку з алгебри

та початків аналізу

в 11 класі

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вчитель: Леонович Н.П.

 

 

2018р.

 Тема

Елементи комбінаторики, теорії ймовірностей та математичної статистики

 

Мета:

• повторити, систематизувати та узагальнити знання основних видів сполук та правил і формул комбінаторики, основних понять теорії ймовірностей та елементів математичної статистики;
• систематизувати вміння застосовувати набуті знання до розв’язування задач, передбачених програмою ЗНО з математики;
• виховувати в учнів працьовитість, вміння долати труднощі;
• розвивати логічне мислення.

Тип уроку: узагальнення та систематизація знань і вмінь.

Хід уроку

І. Організаційний етап.

Провідний педагог Ян Амос Коменський писав: «Вважай нещасливим той день чи той час, в який ти не засвоїв нічого нового і нічого не додав до своєї освіти». Досліджено, що майже половину знань про навколишній світ людина набуває у віці до 5 років. А наступні 10 років вона пізнає про світ майже все і потім свої знання (крім спеціальних) поповнює дуже повільно, в неї з являється доросла звичка - пізнавши щось нове, обов’язково уточнити: «А навіщо це ?»

Сподіваюся, що ви зрозумієте, для чого вам потрібні знання, одержані в школі. Однією із сходинок до цього розуміння нехай буде цей урок. Адже кожен урок для вас - це нові знання та несподіванки, радість перемоги над невідомим. Анрі Пуанкаре вважав, що наука складена з фактів, як будинок з цеглинок. Але зібрання фактів ще не наука, адже куча цегли ще не будинок. Тож нехай ці знання будуть для вас одними з цеглинок, з яких ви збудуєте власний дім.

Сьогодні на уроці ми повторимо і систематизуємо наші знання з теми  «Елементи комбінаторики, теорії ймовірностей та математичної статистики»

ІІ. Перевірка домашнього завдання

Задача 1. Задача 1. Наприкінці останнього тижня навчання зібрали відомості про кількість пропущених уроків математики учнями випускного класу за цей місяць. Отримали такі дані: 2, 5, 0, 1, 6, 3, 0, 1, 5, 4, 0, З, З, 2, 1, 4, 0, 0, 2, З, 6, 0, 3, 0. Побудувати полігон, знайти моду, медіану.

Визначити, яку кількість уроків пропустив у середньому кожен учень.

= –кількість уроків, які пропустив у середньому кожен учень.

Задача 2. З 28 кісток доміно навмання виймають одну. Яка ймовірність того, що а) сума цифр на ній менша 3; б) сума цифр більша 9;  в) обидві цифри на ній парні;  г) обидві цифри непарні?

Відповіді: а) ;     б) ;    в) ;    г)  ;   

ІІІ. Формулювання мети і завдань уроку

IV. Повторення та систематизація знань

 

Теоретичний матеріал

1. Комбінаторні формули:

 

-перестановка (впорядкована множина з n елементів) 

                           

 

-розміщення (впорядкована множина з n елементів по m)

                           

 

-комбінація (будь-яка не впорядкована множина з n елементів по m) 

                         

2. Схема розв’язування комбінаторних задач

Вибір правила:

-правило суми:       А    або    В         (m+n) способами;

-правило добутку:  А     і    В             mn cпособами. 

Вибір формули:

1.Чи всі елементи входять до сполуки?

                 

                 ні                           так       

2.Чи враховується порядок розміщення елементів?

 

                                  

         ні                                   так         

                                                          

         3.Класичне означення  ймовірності:

Р(А)= ,m-число сприятливих елементарних подій;

               n- число всіх рівноможливих подій.

0<Р(А)<1-випадкова подія;

Р(А)=0- неможлива подія;

Р(А)=1-вірогідна подія.

3. Математична статистика:

-частотна таблиця;

-ранжирування ряду; розмах; мода; медіана; середнє значення;

-полігон частот; гістограма (графічне подання інформації).

V.Розв’язування усних вправ

Усні вправи

 

1. Скількома способами можна розподілити:

а) три однакові туристичні путівки між 10 робітниками;

б) три різні туристичні путівки між 10 робітниками;

в) 10 однакових путівок між 10 робітниками;

г) 10 різних путівок між 10 робітниками?

 

2. У шухляді лежать 8 червоних, 2 синіх і 20 зелених олівців. Ви навмання виймаєте олівець. Яка ймовірність того, що це

а) червоний олівець; б) жовтий олівець; в) не зелений олівець. Яку найменшу кількість олівців треба вийняти, щоб із ймовірністю рівною 1, серед них був зелений олівець?

 

3. Тестові завдання містять 5 варіантів відповідей, із яких лише одна правильна. Учень не знає відповіді на 2 тестових завдання і відповідає наугад. Яка ймовірність, що учень а) дасть правильну відповідь на обидва завдання; б) дасть неправильну відповідь на обидва завдання?

VI. Колективне розв’язування задач

Задача 1(ЗНО) .  У місті Х запроваджено 7-цифрову нумерацію телефонів. Пан Карайко має намір зателефонувати до пані Лариси, що проживає в іншому районі міста. Пан Карайко пам’ятає, що всі цифри її телефонного номера різні, але забув три останні з них. Яка ймовірність того, що перша спроба пана Карайка набрати правильний номер буде вдалою?

Задача 2 . Три стрільці, для яких імовірності влучення в мішень дорівнюють 0,8;  0,75;  0,7 роблять по одному пострілу. Знайдіть імовірність того, що жоден із стрільців не влучить.

Задача 3.  У коробці міститься 10 кульок, із них 5 білих. Навмання виймають одну та повертають її назад в коробку. Потім навмання виймають ще одну кульку. Яка ймовірність того, що обидві витягнуті кульки білі?

Задача 4. У коробці міститься 10 кульок, із них 5 білих. Навмання виймають одна за одною дві кульки та назад не повертають. Яка ймовірність того, що обидві витягнуті кульки білі?

VII.Хвилинка відпочинку

Математичний аналіз деяких азартних ігор

Останнім часом проблема азартних ігор набула особливого значення. Соціологами помічено: зростання злочинності серед неповнолітніх у нашій державі співпало з легалізацією азартних ігор. У зв’язку з цим багато дослідників вважають азартні ігри серйозною соціальною проблемою, що становить загрозу для підростаючого покоління. Оскільки в процесі гри у ряді випадків виникають розслаблення, зняття емоційної напруги, відволікання від неприємних проблем і гра розглядається як приємне проведення часу, то виникає механізм поступового втягування і формується ігрова залежність. Близько 60 % гравців переходять у злочинний світ, через скоєні насильницькі дії. У гравця складається борг, який штовхає на шлях позбавлення від нього. Коли з боргом розраховується, то тривога пропадає, і він знову повертається до гри.

На мою думку, профілактикою від гральної залежності є ознайомлення учнів із математичним аналізом азартних ігор. За допомогою математики можна показати, що всі вони мають від’ємне математичне сподівання і тому вигідні для організаторів. Очевидно, що в проектуванні та розробці цих ігор брали участь математики, які й забезпечили власникам казино та гральних залів прибутки, а також убезпечили їх від ризику програти, бо казино, на відміну від гравців, не хоче покладатися на везіння і сліпий випадок. Величезні прибутки, які одержують власники, підтверджують теорію, що гравець із додатним математичним сподіванням виграшу — з імовірністю як завгодно близької до одиниці, може виграти як завгодно багато за достатньо великої кількості партій.

Отже, збанкрутувати казино може тільки в тому випадку, якщо гравці перестануть його відвідувати.

Тому найкраща порада, яку може дати гравцю математика, — запропонувати стратегію, за якої він буде менше програвати. Неможливість створення стовідсоткової виграшної стратегії у грі з від’ємним математичним сподіванням ще не означає неможливість виграти в кожному конкретному випадку, а кожний виграш стимулює до участі в грі, що й призводить до згубного впливу на психологію особистості.

Самостійна робота

Вибери правильний варіант відповіді.

1.   Студенти однієї з груп під час сесії повинні скласти п’ять іспитів. Заступнику декана потрібно призначити складання цих іспитів на п’ять визначених дат. Скільки всього існує різних варіантів розкладу іспитів для цієї групи?

А	Б	В	Г	Д
5	25	60	120	240

2.  Укажіть, скільки можна скласти різних правильних дробів, чисельниками і знаменниками яких є числа 2,3,4,5,6,7,8,9.

А	Б	В	Г	Д
28	56	70	112	Інша відповідь

3.  До складу української Прем’єр-ліги з футболу входять 16 команд. Упродовж сезону кожні 2 команди грають між собою два матчі. Скільки усього матчів буде зіграно за сезон?

 

А	Б	В	Г	Д
120	128	200	240	256

4. Кодовий замок на дверях має десять кнопок, на яких нанесено десять різних цифр (див. рисунок). Щоб відчинити двері, потрібно одночасно натиснути дві кнопки, цифри на яких складають код замка. Скільки всього існує різних варіантів коду замка? Уважайте, що коди, утворені перестановкою цифр (наприклад, 1-2 і 2-1), є однаковими

А	Б	В	Г	Д
100	90	45	20	10

1.5 Пасічник зберігає мед в однакових закритих бідонах. Їх у нього дванадцять: у трьох бідонах міститься квітковий мед, у чотирьох – мед із липи, у п’яти – мед із гречки. Знайдіть ймовірність того що перший навмання відкритий бідон буде містити квітковий мед.

А	Б	В	Г	Д

1.6 З натуральних чисел від 1 до 30 учень навмання називає одне. Яка ймовірність того. що це число є дільником числа 30?

А	Б	В	Г	Д

В уривку художнього твору 47 слів мають різну кількість букв. Укажіть моду даного розподілу за допомогою зображеного на рисунку полігону частот.

 

А	Б	В	Г	Д
2	4	5	8	10

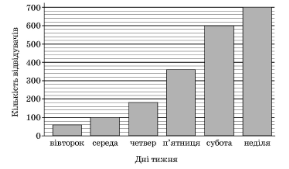
8.  На діаграмі відображено кількість відвідувачів Музею Води протягом одного робочого тижня (з вівторка до неділі). У який день тижня кількість відвідувачів була вдвічі більшою, ніж у попередній день?

 

А	Б	В	Г	Д
середа	четвер	п’ятниця	субота	неділя

 

Завдання на відповідність 1.9 У коробці було 20 карток, пронумерованих числами від 1 до 20. Із коробки навмання взяли одну картку. Яка ймовірність того, що на ній записано просте число                                          А)  0,7 двоцифрове число                                    Б)  число, кратне 5                                          В) число, не кратне 3                                  Г) 0,2                                                                      Д)

Розв’яжи і запиши відповідь у бланк.

2.1  Скільки всього різних двоцифрових чисел можна утворити з цифр 1, 5, 7 і 8 так, щоб у кожному числі всі цифри не повторювалися?

 

2.          Скільки можна скласти різних неправильних дробів, чисельниками і знаменниками яких є числа 2, 3, 5, 7, 11?
3.  У кошику 10 куль. Скільки там білих куль, якщо ймовірність того, що три навмання вибрані кулі будуть білими, дорівнює ?
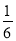4. Іванко та Юрко одночасно й незалежно один від одного купують кавуни. Ймовірність того, що Іванко вибере стиглий кавун дорівнює 0,6, а ймовірність того, що Юрко вибере стиглий кавун дорівнює 0,8.

1. Знайти ймовірність того, що обидва хлопці виберуть стиглі кавуни?
2. Знайти ймовірність того, що хоча б один із хлопців вибере стиглий кавун?

VIII.Робота над заповненням бланку відповідей

Занести відповідь у бланк

 

 

 

 

 

 

ІХ. Поради учням щодо підготовки до ЗНО з математики

До ЗНО залишилося вже зовсім небагато часу, але він є. Ваше завдання – максимально ефективно його використати для підготовки. Головне – не панікувати, не витрачати час на конфлікти та жалість до себе. Що стосується математики, то тут важливо максимально сконцентрувати зусилля і раціонально розподілити час для підготовки, аби уникнути перенавантаження. Важлива частина підготовки до ЗНО з математики – математичні задачі.

Пропоную кілька рекомендацій щодо того, як їх розв’язувати.

Спокійно та уважно прочитайте завдання: не лякайтеся, якщо вам здається, що раніше ви не зустрічалися з таким типом завдань. Почніть із відповідей на запитання, що треба знайти і що дано, які теоретичні відомості вам відомі. Спробуйте розділити завдання на дві частини.

Не дозволяйте собі зразу виконувати завдання, не дочитавши його до кінця. А після вирішення обов’язково ще раз прочитайте завдання і дайте відповідь саме на запитання задачі, а не на те, яке вам спало на думку. Весь час думайте!

Думайте тільки про те завдання, яке ви вирішуєте на цей час, відволічіться від усіх інших.

Складіть схему, план, малюнок, модель: для розв’язання всі засоби підходять.

Згадайте правила й алгоритми, необхідні для вирішення цього завдання.

Уникайте миттєвих помилок: на тестах може перевірятися як ваше вміння застосовувати знання в знайомій ситуації, так і вміння застосовувати їх у незнайомій та новій ситуації. Ви маєте проаналізувати ситуацію і виконати саме те завдання, яке дано.

Так як апетит приходить під час їди, ідеї рішення задач приходять в процесі розв’язання.

Інколи може налякати, що умова задачі дуже велика. Тоді варто уважно прочитати її, пошукати, можливо є варіант розділу завдань на частини.

Коли вирішуєте задачі на чернетці, записуйте всі викладки. Тоді буде легше відшукати помилку у вирішенні.

Пам’ятайте, що за останні місяці перед іспитами ви повинні поставити вчителю максимум теоретичних запитань, які у вас виникають щодо розв’язання задач. А щоб з’ясувати, що для вас залишається складним і незрозумілим, треба якомога більше розв’язувати задач удома.

Бажаю успіху!

Х. Підсумок уроку, рефлексія

ХІ. Домашнє завдання

Повторити «Елементи комбінаторики, теорії ймовірностей та математичної статистики», розв’язати завдання в тестовій формі стор. 324-326.