Конспект уроку з математики для 6 класу на тему: " Відношення. Основна властивість відношення"

Урок №1

Тема уроку. Відношення. Основна властивість відношення

Мета уроку.  Формувати в учнів компетентності:

 математичні: освітні: розширення знань про число введенням поняття відношення як числа; формування культури усних і письмових обчислень;учні повинні  навчитися пояснювати, що таке: відношення; розв’язувати вправи, що передбачають знаходження відношення чисел і величин;

розвивальні:сприяти  розвиток логічного і критичного мислення; пізнавального інтересу; розвитку уваги, пам’яті, логіки, культури мислення та інтуїції;

полікультурну: використання інформації з історії математичних відкритті;

навчально-пізнавальну і дослідницьку: формувати початкові навички володіння методами дослідження практичних задач,  вміння вирішувати проблемні завдання - дослідження основної властивості відношення;             

соціальну і комунікативну:  здатність  продуктивно співпрацювати з  учнями  у групі та команді;  

інформаційну: залучення учнів до використання додаткової літератури, Інтернету , до участі у виконанні творчих завдань;

саморозвитку та самоосвіти:  стимулювання учнів до самостійного здобуття знань – творчі домашні завдання, участь в самоосвітній діяльності.

Спосіб реалізації: через діяльнісний підхід - розвиток умінь і навичок кожного учня,  формування здібностей до колективної діяльності та самоосвіти.

Тип уроку. Урок засвоєння нових знань

Хід уроку

 

І. Організаційний момент.

    Взаємне  вітання вчителя й учнів; перевірка відсутніх; перевірка зовнішнього стану приміщення; перевірка робочих місць та зовнішнього вигляду учнів; організація уваги.

Девіз:

«Без звички працювати, без уміння долати труднощі, без дисципліни праці немає людини. А саме до цього привчає математика» М.І. Кодак.

Саме всі ці якості  нам сьогодні будуть конче необхідні.

ІІ. Перевірка домашнього завдання.

Відповідь на запитання учнів.

Перевірка наявності домашнього завдання у кожного учня.

ІІІ. Повідомлення теми, цілей  і завдань уроку. Актуалізація  і корекція опорних знань.

Сьогодні  ми  починаємо  вивчати нову  тему  і  познайомимося  з  новим  для  вас  поняттям. Що  це  за  поняття  ви  взнаєте, коли розв’яжете  приклади, а  потім  скористаєтесь дешифратором.

(учні виходять  до дошки  парами і вибирають будь-який приклад)

1. 10,12*100 =  2. 10,12 : 100 =         3. 34,8 : 0,2 =          4. 19,45 -2,05

5. 2 * 2 =             6. 2 : 2 =        7. 1*2 =       8.  5 %   від  числа  700.

9. 25%  числа  становлять  4.  Чому  дорівнює  все  число?     10. Запишіть  відсоток  у  вигляді  десяткового  дробу:  16%.

Слайд 2.

Повідомлення теми, цілей  і завдань уроку  Отже, тема нашого уроку «Відношення». 

  Слайд 1

 

ІV. Мотивування учіння.

 При розв’язуванні різноманітних практичних задач часто приходиться порівнювати однорідні величини між собою і знаходити у скільки разів одна величина більша за іншу чи яку частину одна величина становить від іншої. В давнину навіть у середні віки під числом розуміли лише натуральне число. Відношення ж як результат ділення одного числа на друге не сприймали як число.  Але ще в працях середньоазіатського математика Омара Хайяма  (1048-1131) висловлювалась думка, що відношення є число і з ним можна виконувати дії. Чітке визначення відношення числом дав геніальний англійський вчений Ісаак  Ньютон  в 17 столітті.

Сьогодні на уроці  мова піде саме про відношення двох чисел, яке можна виразити числом. На уроці ви повинні засвоїти поняття відношення, його основну властивість.

 

V. Сприймання й усвідомлення учнями фактичного матеріалу

 1.Зараз ми побуваємо в «Кінозалі» (Перегляд проводиться за динамічними кадрами). 

 Зміст кадрів.

Кадр 1.Мотивація учіння.  Постановка проблеми.

 Задача. Для класу закупили 90 зошитів, з них 60 — у клітинку, а решта — у лінійку. У скільки разів усіх зошитів більше, ніж зошитів у клітинку? Яку  частину всіх зошитів становлять зошити у клітинку?

Слайд 3.

 «Мозковий штурм».

1.               Як відповісти на перше запитання? (Висловлюються думки учнів)  і перевіряються  за допомогою кадрів фільму.

Кадр 2. Шляхи вирішення проблеми.

  Щоб знайти, у скільки разів усіх зошитів більше, ніж зошитів у клітинку, потрібно 90 поділити на 60, тобто знайти частку чисел 90 і 60:

90 : 60 = 1,5.

Отже, всіх зошитів у півтора рази більше, ніж зошитів у клітинку.

Частка чисел 90 і 60 вказує, у скільки разів число 90 більше від числа 60.

Кадр 3. (стоп). Яку частину  всіх зошитів становлять зошити в клітинку ?

 (Учні висловлюють свої думки. Варіанти відповідей записуються на дошці). Аналізуються, відсіваються. Може залишитися два варіанти розв’язання.

Кадр №2.(продовження)

 Відповімо на друге запитання задачі.

Оскільки всього є 90 зошитів, то 1 зошит — це 1 дев’яноста частина всіх зошитів, а 60 зошитів — це   , або  всіх зошитів.

 . Отже, зошити у клітинку становлять  всіх зошитів.

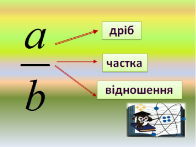
Цю ж відповідь ми могли одержати, якби одразу поділили 60 на 90. Тому частка чисел 60 і 90 вказує, яку частину становить число 60 від числа 90.

Кадр 4.

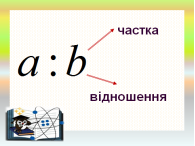
 Щоб відповісти на запитання задачі, нам довелося шукати частки двох чисел. Такі частки називають відношеннями двох чисел.

90 : 60 = 1,5 -  відношення числа 90 до числа 60.

60 : 90 = -   відношення числа 60 до числа 90.

 Яку частину число 60 становить від 90?

Відповідь .В обох випадках ми виконували дію ділення, тобто шукали частку від ділення двох чисел.

Кадр 5 (підсумок )

 Відношенням двох чисел називають частку цих чисел. Відношення вказує, у скільки разів одне число більше від іншого, або яку частину становить одне число від іншого.

 Якщо є дві величини, виміряні однією і тією ж одиницею вимірювання, то відношенням цих величин називають відношення їхніх числових значень.

Наприклад: відношення 6 км до 10 км дорівнює...                          

         6 км : 10 км = 6 : 10 = ,        10 кг : 2 кг = 10:2 = 5.

600 г : 2 кг,     2 кг = 2000 г,   600 : 2000 = 0,3   або 600 г = 0,6 кг,  0,6 : 2 = 0,3.

 Отже, що таке відношення? Як можна записати відношення?

Слайди 4,5,6

 

 

 

 

 

2.Основна властивість відношення. Дослідження проблеми.

Чи зміниться відношення двох чисел, якщо обидва члени відношення помножити або поділити на число, відмінне від нуля?

Зараз ми розділимося на дві групи. Перша група дослідить питання  множення, а друга – ділення.  Ви отримуєте завдання.  (Відповіді учні пишуть на дошці). ( Порада. Відношення краще записувати у вигляді дробу).

 

І група

2:3 =	0,1: 0,4 =
Помножити на 3	На 10	На 6
	(0,1*10):(0,4*10)=1:4	(

 

ІІ група

9:3=
Поділити на	на 2	на 6

 

Чи змінилося відношення при множенні  членів  на одне й теж число?

Чи змінилося відношення при діленні членів  на одне й теж число?

Висновок. Слайд 7.

 

 

 

 

Користуючись цією властивістю, відношення можна спрощувати.

VІ.  Фізкультхвилинка. Учні отримують картки з відношенням. Одна група відношення, а друга  спрощене до нього. Потрібно знайти пару.

9: 3=3:1,  6:4 = 2:3,  7:14=1:2,  25:5 =5:1,  25:15 = 5:3,  35:5 =1:7, 21:14=3:2. 

VІІ.    Осмислення зв'язків і залежностей між елементами вивченого матеріалу.

1. Запишіть за допомогою двокрапки відношення чисел:

а) 3 і 5;   б) 12 і 7; в) 0,5 і 2,5; г) .

2. . Запишіть за допомогою  дробової  риски відношення чисел

а) 2 і 7;   б) 13 і 9;   в) 0,6 і 0,7;  г) 1 і .

3. Чому дорівнює відношення :

а) 204  до 60;  б)   до    в)2   до 1,3.

4. Обчисліть відношення значень величин:

А) 3м : 2м;  б) 1м: 4дм;  в) 10 м: 2 год.

 

VІІІ. Узагальнення і систематизація знань.

 Давайте виділимо основні моменти нашої теми.

1.Означення відношення. Члени відношення.

2.Запис та  читання відношення.

3.Основна властивість відношення.

4. Відношення іменованих величин.

 

 

                                               Слайд 8.

 Відношення різнорідних величин – це величина, значення якої залежить від вибору одиниць вимірювання величин, що є членами відношення

Ми вже використовували цю властивість, коли розв’язували задачі на рух. Давайте пригадаємо, що  швидкість – це відношення пройденої відстані до часу

VIII. Підсумок. Рефлексія.

1.Інтерактивна вправа «Незакінчені речення»

Я починаю  речення, а ви його закінчуєте.

◊ Сьогодні на уроці ми навчилися …

◊ Сьогодні на уроці мені було цікаво тому, що …

◊ Я думаю, мені ще необхідно попрацювати над …

◊ Я сьогодні поповнив свої знання тим, що …

Творче завдання.

Скласти «Юридичну шпаргалку». Головна умова: охопити всі важливі моменти; її повинні зрозуміти  учні.

3.               Оголошується тема творчого  завдання - «Золота пропорція»

Утворюються групи:

 

 

 

 

Слайд 9.

 Група «Теоретики» готує  презентацію   з теоретичного матеріалу теми; «Відношення і пропорція» ; група «Золота пропорція» - з теми «Золота пропорція», група «Гармонія» - про «Золотий переріз у мистецтві, архітектурі, скульптурі», група  «Досконалість» - « Золота пропорція у природі»