Контрольна робота "Інтеграл"

Варіант 2

1. Яка з поданих функцій є первісною функції

А) F(x) =    Б)  F(x) =     В)  F(x) =   Г)  F(x) =

2. Обчисліть інтеграл  

А)                Б) -             В)           Г) -   

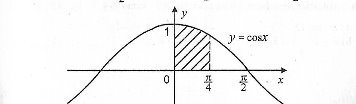
3. Обчисліть площу заштрихованої фігури, зображеної на рисунку

А)    1        Б)                В)              Г)

4. Знайдіть первісну функції f(x)= 3 – 2x +3 , графік якої проходить через точку М(1; -3).

5. Обчисліть інтеграл:

1) ;    3)

2) ;

6. Задано функції f(x) = 5 -    і   g(x) = 3 – x.

     1. Побудуйте абсциси точок перетину графіків

         функцій.

     2. У прямокутній системі координат побудуйте

         графіки цих функцій.

     3. Обчисліть площу фігури, обмеженої цими

         графіками.

7. Використовуючи геометричний зміст інтеграла, обчисліть  dx

Варіант 1

1. Знайдіть загальний вигляд первісної функції

А)  + С ;  Б)    + C ;   В) + C ;  Г)  6x + C.

2. Обчисліть інтеграл  

А)  1,5;              Б) 0,5;          В)  - 1,5;      Г) -  

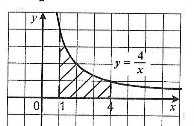
3. Обчисліть площу заштрихованої фігури, зображеної на рисунку

А)    4        Б)               В)  4          Г) -4         

4. Знайдіть первісну функції f(x)= 3 – 6x - 2,     графік якої проходить через точку М(1; 4).

5. Обчисліть інтеграл:

1) ;    3) dx.

2) ;

6. Задано функції f(x) = 6 -    і   g(x)= x + 4.

     1. Побудуйте абсциси точок перетину графіків

         функцій.

     2. У прямокутній системі координат побудуйте

         графіки цих функцій.

     3. Обчисліть площу фігури, обмеженої цими

         графіками.

7. Використовуючи геометричний зміст інтеграла, обчисліть  dx.