Контрольна робота "Інтеграл"
Контрольна робота № 5
Тема «Інтеграл»
В – 1 1 частина
- Знайти загальний вигляд первісних для функції f(x) = – 4 cos x
А) – 4 ![]() + С; Б) 4
+ С; Б) 4 ![]() + С; В) – 4
+ С; В) – 4 ![]() + С; Г) ) 4
+ С; Г) ) 4 ![]() + С;
+ С;
-
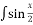 dx = …
dx = …
А) 2 ![]() + C; Б) –
+ C; Б) – ![]()
![]() + С; В)
+ С; В) ![]()
![]() + С; Г) – 2
+ С; Г) – 2 ![]() + С;
+ С;
- Тіло рухається прямолінійно зі швидкістю V(t) = 2t + 1. Знайти закон руху тіла S(t), якщо S(1) = 3.
А) t2+ t + 3; Б) t2+ t ; В) t2+ t +1; Г) t2+ t +2; Д) t2+ t – 1.
-
Обчислити інтеграл
 dx.
dx.
А) 2; Б) – ![]() ; В)
; В) ![]() ; Г) –2 Д)0.
; Г) –2 Д)0.
- Установити відповідність між невизначеними інтегралами (1 – 4 )та їхніми значеннями (А-Д):
-
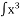 dx А) 3х2 + C
dx А) 3х2 + C
-
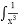 dx Б) –6x2 + C
dx Б) –6x2 + C
-
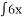 dx В) 12
dx В) 12 + C
+ C
-
 dx Г)
dx Г)  + C; Д) –
+ C; Д) –  + C
+ C
2 частина
|
1 – 2 рівні |
|
|
6. Найти загальний вигляд первісних для функції f(x) = 4 x3 – x + 2 |
6. Найти загальний вигляд первісних для функції f(x) = 4 |
|
7. Для функції f(x) = 3х2 знайти первісну F(x), графік якої проходить через точку А(2;10). |
7. Для функції f(x) = |
|
8. Обчислити: а)
Б)
В)
|
8. Обчислити: а)
Б)
В) |
|
9.Точка рухається прямолінійно із швидкістю V(t) = 6t – t2 (м/с). Знайти відстань, що пройшла точка від початку руху до його зупинки. |
9.Точка рухається прямолінійно з прискоренням a(t) = 6t2 – 2. Знайти: 1) миттєву швидкість V(t), якщо в момент часу t = 1с її швидкість дорівнювала 3 м/с 2)закон руху S(t) точки, якщо S(2) = 9м. |
Контрольна робота № 5
Тема «Інтеграл»
В – 2 1 частина
- Знайти загальний вигляд первісних для функції f(x) = – 4sin x
А) – 4 ![]() + С; Б) 4
+ С; Б) 4 ![]() + С; В) – 4
+ С; В) – 4 ![]() + С; Г) ) 4
+ С; Г) ) 4 ![]() + С;
+ С;
-
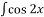 dx = …
dx = …
А) 2![]() + C; Б) –
+ C; Б) – ![]()
![]() + С; В)
+ С; В) ![]()
![]() + С; Г) 2
+ С; Г) 2 ![]() + С;
+ С;
- Тіло рухається прямолінійно зі швидкістю V(t) = 2t + 1. Знайти закон руху тіла S(t), якщо S(1) = 3.
А) t2+ t; Б) t2+ t + 1; В) t2+ t +3; Г) t2+ t +2; Д) t2+ t – 1.
-
Обчислити інтеграл
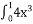 dx.
dx.
А) 1; Б) – ![]() ; В)
; В) ![]() ; Г) –
; Г) –![]() Д) 0.
Д) 0.
- Установити відповідність між невизначеними інтегралами (1 – 4 )та їхніми значеннями (А-Д):
-
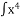 dx А) х2+ C
dx А) х2+ C
-
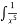 dx Б) –
dx Б) –  + C
+ C
-
 dx В)
dx В) 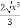 + C
+ C
-
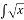 dx Г)
dx Г) 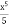 + C; Д) 2х2 + C.
+ C; Д) 2х2 + C.
2 частина
|
3– 4 рівні |
|
6. Найти загальний вигляд первісних для функції f(x) = 3 x2 –5 x – 4 |
6. Найти загальний вигляд первісних для функції f(x) = 4 |
|
7. Для функції f(x) = 2х3 знайти первісну F(x), графік якої проходить через точку А(2;2). |
7. Для функції f(x) = |
|
8. Обчислити: а)
Б)
В)
|
8. Обчислити: а)
Б)
В) |
|
9.Точка рухається прямолінійно із швидкістю V(t) = 3t – t2 (м/с). Знайти відстань, що пройшла точка від початку руху до його зупинки. |
9.Точка рухається прямолінійно з прискоренням a(t) = 6t2 – 2. Знайти: 1) миттєву швидкість V(t), якщо в момент часу t = 1с її швидкість дорівнювала 3 м/с 2)закон руху S(t) точки, якщо S(2) = 9м. |


про публікацію авторської розробки
Додати розробку
