Урок "Метод інтервалів"

Про матеріал

Мета: - повторити розв’язування нерівностей методом інтервалів; - розвивати логічне мислення, вміння знаходити нестандартний , творчий та раціональний підхід до виконання завдання; вміння аналізувати умову завдання, аргументовано висловлювати свою думку; - виховувати наполегливість, старанність та охайність під час математичних записів.

Перегляд файлу

Тема «Метод інтервалів»

Мета: - повторити розв’язування нерівностей методом інтервалів;

розвивати логічне мислення, вміння знаходити нестандартний , творчий та раціональний підхід до виконання завдання; вміння аналізувати умову завдання, аргументовано висловлювати свою думку;
виховувати наполегливість, старанність та охайність під час математичних записів.

Обладнання: комп’ютер, опорні конспекти, плакати, картки , смайлики

І. Орг. момент.

Добрий день. Як справи з настроєм? До уроку готові?

Сьогодні нам знадобиться такий вантаж: хороший настрій, світлий розум, кмітливість і звичайно ж математичні знання, отримані в курсі вивчення алгебри. Памятаємо що:

Я – думаю,я- знаю, я -можу, я -творча особистість.……….

ІІ. Усний рахунок. Розпочинати будь-яку справу потрібно з підготовки до роботи. Отож зараз інтелектуальна розминка : усний рахунок «Єралаш» - ще один крок у підготовці до ЗНО.

1) ( )^-31 – відповідь до №1 з д/з5) 10

2) – х + 1 ˃ 0 х˂1 – відповідь до №2а 6) – х² - 4х +12˂0 (-∞;-6)ᴗ(2;∞) до 2в

3) -1 7) х -у = 5 (6;8) до 2г

4)3х + 4 – х² ≥0 [- 1;4] до 2б х +у = 7

8) 12

ІІІ.Актуалізація опорних знань.

1. Перевірка домашнього завдання

- Давайте перевіримо домашнє завдання.

На яку тему було завдання. (Квадратні та лінійні нерівності). . Чи були труднощі у виконанні завдань?

2. Фронтальне опитування

1. При розв’язуванні лінійних нерівностей ви використовували певні властивості. Давайте їх нагадаємо. Вправа «Закінчити думку»

Я почну правило а ви його закінчите…..

Якщо до обох частин нерівності додати або відняти одне і те ж число, то…
Якщо обидві частини нерівності помножити або поділити на одне і теж додатнє число, то…
Якщо обидві частини нерівності помножити або поділити на одне і теж від’ємне число, то…
Якщо х ˃ у, то за …..

2. Як розв’язували квадратні нерівності? Яким способом? (графічним).

3. Що потрібно знати для цього?.

Перевіримо правильність.( Відповіді до завдань.)

А чи не зустрічали ви сьогодні знайомих результатів у завданнях?

Є відповіді до №1, №2а ,№2б, №2в , №2г.

До №3а розв’язком нерівності є проміжок ( -2; 1), до №3б [-; 1] або [- 4; 1].

ІІІ. Мотивація. Багато завдань у математиці розв’язуються декількома способами. Ми повинні вибрати який? (Раціональний) Чому? (зекономити час) .Девіз нашого уроку буде. «Недостатньо мати тільки добрий розум, головне раціонально його використовувати» Так сказав Рене Декарт французький філософ , фізик , фізіолог , математик ,.Коли ми про нього вперше почули?.

Маємо нерівність (Х + 3)(Х – 1)(Х – 2) ˃ 0. (Х + 3)(Х – 1) ˃ 0

(Х – 2)

Коли добуток або частка буде додатнім + + + або + - - або - - + або - + -або…

Отож потрібно розглянути багато варіантів і це займе багато часу.

Щоб розв’язати швидше використаємо «Метод інтервалів». Нагадаємо в чому він полягає. У вас на партах є опорні конспекти, які допоможуть вам нагадати цей метод. Ми вивчали його у 10 класі

ÐÐ¾Ð²âÑÐ·Ð°Ð½Ðµ Ð·Ð¾Ð±ÑÐ°Ð¶ÐµÐ½Ð½Ñ

ІУ. Формування вмінь та навичок

1. Розглянемо приклад №1 з конспекту.

2. Учень біля дошки розв’язує нерівність: (Х +3)(Х – 1)(Х – 2) ˃ 0.

Відповідь: ( -3;1)ᴗ (2;∞).

3. Розглянемо приклад №2 з конспекту.

4. Скільки цілих розв’язків має нерівність + ≤ 1.

Чи схожа нерівність на приклад? Проблема! Як же її розв’язати? (Відповідь учнів). Учень біля дошки розв’язує. (Нагадати про чергування знаків.) Отримали проміжки Відповідь: 8 розв’язків

5. Робота в парах. Якщо пара справляється, записує розвязок на дошці. Якщо відповідь правильна, то частину вислову відкриває. Отримавши всі правильні відповіді, прочитаємо вислів.

Завдання різнорівневі.

І. а) (х-2)(х -5)(х– 12)˃0 (2;5) ᴗ (12; ∞)

Б) ≤ 0 [ - ; 3)

ІІ. а) (3 –х)(4 –х²) ˃ 0 (-2;2) ᴗ (3; ∞)

Б) ≤ 0 [- 1; 1) ᴗ (1;5)

В) ≥ 0 ( -∞; - 3) ᴗ{-} ᴗ (1; ∞)

(Скласти, прочитати і обговорити вислів) «Якщо ви не той, що на вершині, це не значить, що ви той що внизу»

Фізкультхвилинка

6. Розвязати нерівність:

˂ 0.

Працюємо по алгоритму.

(Учень біля дощки). Другий множник чисельника нулів немає, бо дискримінант відємний. Графік функції парабола, вітки якої напрямлені вгору. Отож наш вираз завжди додатній. За властивістю нерівності ми можемо обидві її частини поділити на додатній вираз. Отримаємо нерівність

˂ 0. Розвяжемо її знайомим нам методом інтервалів. Відповідь: (- 7; 8). Отож ми використали не тільки метод інтервалів, а і математичний аналіз.

7. «Творча майстерня» В попередніх завдання ми розв’язували нерівності і отримували відповіді. А ось хотіла вам запропонувати ще одну нерівність та трапилась прикрість. Умова пропала, залишилась тільки відповідь. Всі дійсні числа крім числа 9. Допоможіть відтворити умову

У. Рефлексія.

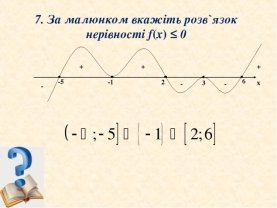
Підведемо підсумок. Що ми повторювали сьогодні? Для закріплення розглянемо такі вправи. (Завдання на слайдах показати. Усне розв’язування.)

УІ. Підсумок уроку.

Виставити оцінки. На слідуючому уроці онлайн – тестування по темі «Нерівності». Ви отримаєте індивідуальні завдання. Будете розв’язувати їх в зошиті. Результат запишете. Якщо половина, то 6б. Ю то 9б. якщо більше високий рівень.

УІІ. Домашнє завдання – робота над помилками тестів. В кого помилок не буде: з підручника Є.П.Неліна «Алгебра профільний рівень)ст. 407 №35(1), №36(2;4) №37(1)

1. ÐÐ»Ñ ÑÐº0Ñ Ð· ÑÐ¸Ñ Ð½ÐµÑÑÐ²Ð½Ð¾ÑÑÐµÐ¹ Ð¿ÑÐ°ÑÑÑ Ð¼ÐµÑÐ¾Ð´ ÑÐ½ÑÐµÑÐ²Ð°Ð»ÑÐ²? 1. 3Ñ + 5 â¥ 0 (x â 3)(x + 2) < 0 2. 4. 5. 6. 3. 2. ÐÐ¸Ð±ÐµÑÑÑÑ Ð¿Ð¾ÑÐ»ÑÐ´Ð¾Ð²Ð½Ð¾ ÐºÑÐ¾ÐºÐ¸ Ð´Ð»Ñ ÑÐ¾Ð·Ð²âÑÐ·ÑÐ²Ð°Ð½Ð½Ñ Ð½ÐµÑÑÐ²Ð½Ð¾ÑÑÑ f(x) > 0 Ð¼ÐµÑÐ¾Ð´Ð¾Ð¼ ÑÐ½ÑÐµÑÐ²Ð°Ð»ÑÐ² ÐÐ½Ð°Ð¹ÑÐ¸ Ð½ÑÐ»Ñ ÑÑÐ½ÐºÑÑÑ f(x) ÐÐ½Ð°Ð¹ÑÐ¸ Ð¾Ð±Ð»Ð°ÑÑÑ Ð²Ð¸Ð·Ð½Ð°ÑÐµÐ½Ð½Ñ ÑÑÐ½ÐºÑÑÑ f(... 7. ÐÐ° Ð¼Ð°Ð»ÑÐ½ÐºÐ¾Ð¼ Ð²ÐºÐ°Ð¶ÑÑÑ ÑÐ¾Ð·Ð²`ÑÐ·Ð¾Ðº Ð½ÐµÑÑÐ²Ð½Ð¾ÑÑÑ f(x) â¤ 0 Ñ 6 2 -1 3 -5 + + + - - - 1 2 3 4 5 6 7 8 -7 -6 -5 -4 -3 -2 -1 7 6 5 4 3 2 1 -1 -2 -3 -4 10. Ð¤ÑÐ½ÐºÑÑÑ y = f(x) Ð²Ð¸Ð·Ð½Ð°ÑÐµÐ½Ð° Ð½Ð° [-7; 7]. ÐÐ½Ð°Ð¹Ð´ÑÑÑ ÑÐ¾Ð·Ð²á¾½ÑÐ·ÐºÐ¸ Ð½ÐµÑÑÐ²Ð½Ð¾ÑÑÑ f(x) < 0. Ð... 3. ÐÐµÑÐµÐ²ÑÑÑÐµ Ð¿ÑÐ°Ð²Ð¸Ð»ÑÐ½ÑÑÑÑ ÑÐ¾Ð·Ð²á¾½ÑÐ·Ð°Ð½Ð½Ñ Ð½ÐµÑÑÐ²Ð½Ð¾ÑÑÑ (x â 3)(x + 2) < 0 f(x) = (x â 3)(x + 2) D(f): R -2 3 X