Урок "Застосування похідної в задачах екологічної безпеки"

Тема уроку: Застосування похідної в задачах екологічної безпеки

Мета: Навчальна:розвиток практичних навичок використання теоретичних знань з теми «Похідна та її застосування» до розв’язування задач екологічного змісту.

Розвиваюча: розвиток уміння працювати в команді, активно слухати, поважати чужу думку, прагнення до наукової творчості

Виховна: формувати виважене ставлення до навколишнього середовища, усвідомлення змісту екологічної безпеки, нести соціальну відповідальність за прийняті рішення.

Ключові компетентності:

• Математична – уміння розв’язувати прикладні задачі за темою «Похідна та її застосування»
• Спілкування державною мовою: доречно та коротко вживати математичні терміни, зрозуміло формувати думку, аналізувати результати, доводити правильність твердження.
• Уміння вчитися впродовж життя: усвідомлювати основні потреби та цінність нових знань.

Тип уроку:  урок закріплення та узагальнення навчального матеріалу

Форма проведення:  семінар з елементами проектної діяльності

       Епіграф уроку: Вся глибина думки, яка закладена у формулювання математичних понять, згодом розкривається тим умінням, з яким ці поняття використовуються. (Е. Вігнер).

Хід уроку :

1. Організацій момент
2. Мотивація  діяльності

Математичні задачі з практичним змістом - це такі завдання, які пов'язані з застосуванням математики в техніці, хімії, економіці, медицини, екології, а також у побуті. Ми розглянемо завдання, які можна вирішити за допомогою похідної. Ці завдання не зовсім звичайні як за формою викладу, так і по методам розв'язування.

Одним з найважливіших понять математичного аналізу є похідна функції. Похідна характеризує швидкість зміни функції по відношенню до зміни незалежної змінної. В геометрії похідна характеризує кривизну графіка, в механіці - швидкість нерівномірного прямолінійного руху, в біології - швидкість розмноження колонії мікроорганізмів, в економіці - вихід продукту на одиницю витрат, в хімії - швидкість хімічної реакції.

При вирішенні конкретних задач доводиться мати справу з величинами, числові значення яких отримані шляхом вимірів і, отже, точне їх значення невідомо. Якщо вихідні дані містять похибки вимірювань, то застосування точних методів вимірювання не доцільно. Для спрощення і полегшення обчислень в таких випадках краще використовувати наближені методи. Теоретичною основою одного з найпростіших прийомів наближених значень обчислень є поняття диференціала. Наближене значення приросту функції називається диференціалом функції. Серед багатьох завдань, що вирішуються за допомогою похідної, найбільш важливим є завдання знаходження екстремуму функції і пов'язане з нею завдання знаходження найбільшого (найменшого) значення відповідних функцій.

Найдоцільнішими з інновацій є проектно-тематичний підхід до організації навчального процесу. Метод проектів стимулює розвиток пізнавальних  здібностей  учнів  та спрямуванню  їх вмінь самостійно знаходити  алгоритм розв’язання задач та аналізувати  отримані результати.

«Екологічна безпека й сталий розвиток» - лінія, яка спрямована  на формування в учнів відповідального ставлення до навколишнього середовища.

3. Актуалізація знань 

Усне опитування за схемою (рис. 2.1) та заповнення таблиці «Знаю- хочу дізнатися»

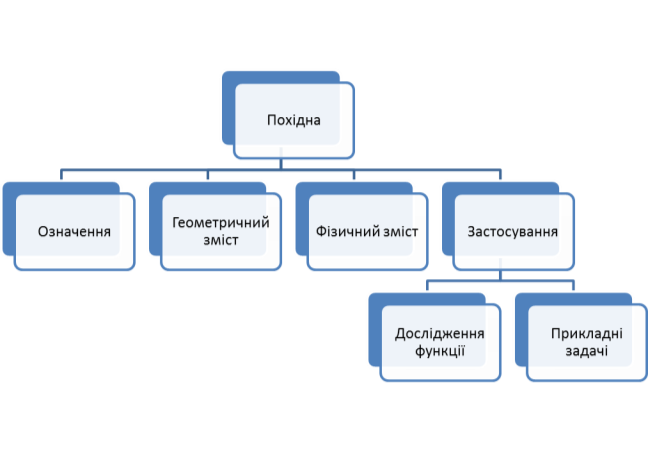
Таблиця «Знаю – хочу дізнатися»

4. Проведення семінару

Задачі, які ми будемо розв’язувати сьогодні так чи інакше пов’язані з екологією.

Екологія – це захист повітря, води, грунту, лісів, тварин, так щоб наслідки діяльності людини не призвели до загибелі нашої планети.

У нас сьогодні відкрите засідання Малої Академії Наук (МАН), яке ми проводимо у вигляді  семінару. Ми розглянемо задачі прикладного характеру і покажемо, як застосування похідної, допоможе нам їх розв’язати.

 Ви поділені на 5 наукових секцій: біології , квітникарства, гігієни та санітарії, фізики та хімії,географії та екології . Кожна секція підібрала задачу, яку можна розв’язати за допомогою похідної.

 Доповідають голови методичних об’єднань.

І.  Секція «Квітникарства».

 У земляну суміш вводять популяцію  з 1000 бактерій.

Чисельність популяції  зростає за законом:_p(t)=1000+1000t/(100+t² ), t – час, в годинах. Знайти в який час буде максимальний розмір популяції.

__________________________________________________________________

Відповідь: максимальна чисельність бактерій буде через 10 годин и складатиме  1050.

ІІ. Секція «Біології»

Закон накопичення поживних речовин  у цибулинах тюльпанів  визначається рівнянням y(x)= -0.0002x² + 0.006x, де х кількість днів від появи зелених ростків до закінчення цвітіння. З’ясуйте, через кілька днів накопичення поживних речовин в цибулині буде максимальним.

_______________________________________________________________

 Відповідь : через 15 днів.

ІІІ. Секція «Гігієна та санітарія»

 Кількість людей, які під час епідемії грипу захворюють за один день, обчислюється за формулою: N(t)=0,003t(50-t) (швидкість поширення епідемії).

На який день епідемія  досягне максимуму?
Через кілька днів епідемія згасне ?

__________________________________________________________________

Відповідь:максимальна кількість захворілих буде на 25 день;

                 епідемія згасне через 50 днів.

IV.  Секція « Хімії та фізики» 

 Залежність між кількістю речовини, що отримується в результаті  деякої хімічної реакції і часом (в секундах) виражається рівнянням : Q(t)=A(1+е^t).

Яка буде швидкість хімічної реакції в момент часу 3 секунди?

А- молярна маса СО₂.  Для нашої задачі Q(t)=44(1+е^t).

_____________________________________________________________________________

Відповідь : швидкість буде  44*е³

V.  Секція  «Географії та екології»

  Відповідь: з висоти 2015 метрів.

Засідання нашої МАН закінчено. Пропоную проект рішення:

Можна вважати, що дії щодо моделювання  процесів дійсності повністю сформовано в учнів, бо ви можете за умови повної самостійності :

1. Перевести задачу на мову математики;

б) Сконструювати математичну задачу;

в) Виділити провідну математичну ідею та алгоритм розв’язуваняя задачі;

г) Критично осмислити отриманий результат.

Питання до групи  «Яка задача вас найбільше вразила ?».

5. Розв’язування тестів у форматі ЗНО

Самостійна робота учнів

6.  .Практична робота

Кожна група отримує кольоровий картон і треба ,на їх думку,зробити вазон найбільшого об’єму. Учні працюють з картоном, ножицями, клеєм та обчислюють об’єм, отриманого вазона.

Після обговорення результатів, учитель показує на дошці рішення задачі за допомогою похідної.

7. Підсумки уроку

• Над якою темою ми працювали?
• Про що ви дізналися, готуючись до уроку?
• Чим запам’ятається вам цей урок?

8. Оцінювання учнів. Відповіді на їх питання.

9. Домашнє завдання: повторити формули обчислення площі трапеції.

Відповіді на тест ЗНО:

Завдання 9