Контрольна робота з теми: Показникова функція
Варіант 1.
1. Порівняти числа: а) 50,4 і 50,7; б) 
і 
.
2. Порівняти основу a > 0 з одиницею, якщо:
а) a7 < a9; б) a10 < a5.
3. Розв’язати графічно рівняння 
.
4. Розв’язати рівняння:
А) 4x – 3 2x + 2 = 0.
Б) 4x + 1 – 4x – 4x – 1 = 44;
В)
.
5. Розв’язати нерівність
а) 2x + 1 + 2x > 24; б) 
.
В) 
.
.
Варіант 2.
1. Порівняти числа: а) 70,9 і 71,2; б) 
і 
.
2. Порівняти основу a > 0 з одиницею, якщо:
а) a14 < a19; б) a7 < a3.
3. Розв’язати графічно рівняння 
.
4. Розв’язати рівняння:
А). 9x – 4 3x + 3 = 0.
Б) 5x + 1 – 5x + 5x – 1 = 105;
В)
.
5. Розв’язати нерівність
а) 3x + 2 + 3x ‑ 1 > 28; б) 
.
В) 
.
Варіант 1.
1. Порівняти числа: а) 50,4 і 50,7; б) і .
2. Порівняти основу a > 0 з одиницею, якщо:
а) a7 < a9; б) a10 < a5.
3. Розв’язати графічно рівняння .
4. Розв’язати рівняння:
А) 4x – 3 2x + 2 = 0.
Б) 4x + 1 – 4x – 4x – 1 = 44;
В).
5. Розв’язати нерівність
а) 2x + 1 + 2x > 24; б) .
В) .
.
Варіант 2.
1. Порівняти числа: а) 70,9 і 71,2; б) і .
2. Порівняти основу a > 0 з одиницею, якщо:
а) a14 < a19; б) a7 < a3.
3. Розв’язати графічно рівняння .
4. Розв’язати рівняння:
А). 9x – 4 3x + 3 = 0.
Б) 5x + 1 – 5x + 5x – 1 = 105;
В).
5. Розв’язати нерівність
а) 3x + 2 + 3x ‑ 1 > 28; б) .
В) .
Варіант 1.
1. Порівняти числа: а) 50,4 і 50,7; б) і .
2. Порівняти основу a > 0 з одиницею, якщо:
а) a7 < a9; б) a10 < a5.
3. Розв’язати графічно рівняння .
4. Розв’язати рівняння:
А) 4x – 3 2x + 2 = 0.
Б) 4x + 1 – 4x – 4x – 1 = 44;
В).
5. Розв’язати нерівність
а) 2x + 1 + 2x > 24; б) .
В) .
.
Варіант 2.
1. Порівняти числа: а) 70,9 і 71,2; б) і .
2. Порівняти основу a > 0 з одиницею, якщо:
а) a14 < a19; б) a7 < a3.
3. Розв’язати графічно рівняння .
4. Розв’язати рівняння:
А). 9x – 4 3x + 3 = 0.
Б) 5x + 1 – 5x + 5x – 1 = 105;
В).
5. Розв’язати нерівність
а) 3x + 2 + 3x ‑ 1 > 28; б) .
В) .
ТЕМА 16. ПОКАЗНИКОВІ НЕРІВНОСТІ
Самостійні роботи
№ 77. Варіант 1.
Середній рівень
Розв’язати нерівність:
1. 1) 
; 2) 
.
2. 53x ‑ 1 < 25. 3. 
.
Достатній рівень
Розв’язати нерівність (1 — 2):
1. 1) 2x + 1 + 2x > 24; 2) .
2. 4x – 6 2x + 8 < 0.
3. Розв’язати графічно нерівність 2x > 3 ‑ x.
Високий рівень
Розв’язати нерівність:
1. 1) x2 3x – 3x + 1 
; 2) 4x 5 + 2 25x 
.
2. 
.
3. Розв’язати графічно нерівність 
.
№ 78. Варіант 2.
Середній рівень
Розв’язати нерівність:
1. 1) 
; 2) 
.
2. 
. 3. 
.
Достатній рівень
Розв’язати нерівність (1 — 2):
1. 1) 3x + 2 + 3x ‑ 1 > 28; 2) .
2. 4x – 2x < 12.
3. Розв’язати графічно нерівність 
.
Високий рівень
Розв’язати нерівність:
1. 1) 22 + x ‑ 2x + 3 – 2x + 4 > 5x + 1 – 5x + 2; 2) 2x + 23 ‑ x <9;.
2. 
.
3. Розв’язати графічно нерівність 
.
№ 79. Варіант 3.
Середній рівень
Розв’язати нерівність:
1. 1) 
; 2) 
.
2. 102x + 1 < 0,1. 3. 
.
Достатній рівень
Розв’язати нерівність (1 — 2):
1. 1) 3x + 2 + 3x < 30; 2) 
.
2. 
.
3. Розв’язати графічно нерівність 
.
Високий рівень
Розв’язати нерівність:
1. 1) x2 0,2x – 0,2x + 2 < 0; 2) 3x + 32 ‑ x > 10.
2. 
.
3. Розв’язати графічно нерівність 
.
№ 80. Варіант 4.
Середній рівень
Розв’язати нерівність:
1. 1) 
; 2) 
.
2. 103x + 1 > 0,001. 3. 
.
Достатній рівень
Розв’язати нерівність (1 — 2):
1. 1) 5x + 1 – 3 5x ‑ 2 < 122; 2) 
.
2. 3 9x + 11 3x < 4.
3. Розв’язати графічно нерівність 
.
Високий рівень
Розв’язати нерівність:
1. 1) 
; 2) 22 + x + 22 ‑ x > 15.
2. 
.
3. Розв’язати графічно нерівність 
.
Тематичне оцінювання: теми 14 — 16
Контрольна робота 5
№ 81. Варіант 1.
Середній рівень
1. 1) Побудувати графік функції y = 4x і записати її властивості.
2) Розв’язати рівняння 
.
Розв’язати нерівність:
3) 
; 4) 
.
Розв’язати рівняння (2 — 3):
2. 7x + 2 – 7x = 42.
3. 25x – 6 5x + 5 = 0.
Достатній рівень
1. 1) Побудувати графік функції 
і записати її властивості.
2) Розв’язати рівняння 4x + 2x + 1 = 80.
3) Розв’язати нерівність 
.
2. Розв’язати нерівність 
.
3. Розв’язати систему рівнянь 
Високий рівень
1. 1) Побудувати графік функції y = 2x ‑ 3 – 1.
2) Розв’язати рівняння 7 49x + 5 14x = 2 4x.
3) Розв’язати нерівність 2x – 23 – x > 2
2. Розв’язати систему рівнянь 
.
3. Побудувати графік функції y = 0,5|x|.
№ 82. Варіант 2.
Середній рівень
1. 1) Побудувати графік функції y = 4x і записати її властивості.
2) Розв’язати рівняння 
.
Розв’язати нерівність:
3) 
; 4) 
.
Розв’язати рівняння (2 — 3):
2. 3x + 2 + 3x = 270.
3. 4x – 9 2x + 8 = 0.
Достатній рівень
1. 1) Побудувати графік функції 
і записати її властивості.
2) Розв’язати рівняння 22x + 1 + 2x + 2 = 16.
3) Розв’язати нерівність .
2. Розв’язати нерівність 
.
3. Розв’язати систему рівнянь 
Високий рівень
1. 1) Побудувати графік функції y = 2x + 4 – 1.
2) Розв’язати рівняння 3 9x = 2 15x + 5 25x.
3) Розв’язати нерівність 31 + x + 32 – x < 28.
2. Розв’язати систему рівнянь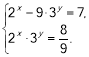 
.
3. Побудувати графік функції 
.
№ 83. Варіант 3.
Середній рівень
1. 1) Побудувати графік функції y = 5x і записати її властивості.
2) Розв’язати рівняння 7x + 4 – 1 = 0.
Розв’язати нерівність:
3) 25x ‑ 1 < 32; 4) 
.
Розв’язати рівняння (2 — 3):
2. 5x + 2 – 5x = 120.
3. 9x – 10 3x + 9 = 0.
Достатній рівень
1. 1) Побудувати графік функції 
і записати її властивості.
2) Розв’язати рівняння 3x + 2 + 9x + 1 – 810 = 0.
3) Розв’язати нерівність 
.
2. Розв’язати нерівність 
.
3. Розв’язати систему рівнянь 
Високий рівень
1. 1) Побудувати графік функції 
.
2) Розв’язати рівняння 2 25x ‑ 5 10x + 2 4x = 0
3) Розв’язати нерівність 5x – 51 – x < 4.
2. Розв’язати систему рівнянь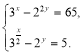 
.
3. Побудувати графік функції y = 4|x|.
№ 84. Варіант 4.
Середній рівень
1. 1) Побудувати графік функції y = 
і записати її властивості.
2) Розв’язати рівняння 92x ‑ 1 – 1 = 0.
Розв’язати нерівність:
3) 103x ‑ 1 > 100000; 4) 
.
Розв’язати рівняння (2 — 3):
2. 2x + 3 + 2x = 36.
3. 9x – 7 3x ‑ 18 = 0.
Достатній рівень
1. 1) Побудувати графік функції 
і записати її властивості.
2) Розв’язати рівняння 3x + 2 + 9x + 1 – 108 = 0.
3) Розв’язати нерівність .
2. Розв’язати нерівність 
.
3. Розв’язати систему рівнянь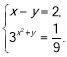 
Високий рівень
1. 1) Побудувати графік функції 
.
2) Розв’язати рівняння 2 4x ‑ 5 6x + 3 9x = 0
3) Розв’язати нерівність 5‑x – 5 x + 2 > 24.
2. Розв’язати систему рівнянь 
.
3. Побудувати графік функції y = 5|x|.
-
-
Чудова контрольна. Все так як і треба.
про публікацію авторської розробки
Додати розробку