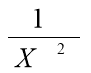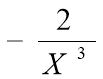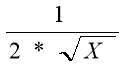Урок Екстремальні точки функції
Сучасний урок – кейс метод « Екстремальні точки »
Клас - 11
Час заняття - 2 години
Тип кейсу – аналітичний (Case-incident method)
Вид кейсу – учбовий.
Тема : Екстремальні точки
Мета уроку:
навчальна:повторити і систематизувати знання учнів 11-го класу по темі :
« Екстремальні точки », формувати навички практичного
застосування отриманих знань;
розвивальна: розвивати знання учнів про похідну, формувати навички
контролю; розвивати логічне, системне та алгоритмічне
мислення, увагу, пам’ять, здатність до самостійності мислення;
виховна: виховувати любов та зацікавленість до математики, сприяти
всебічному розвитку особистості, виховувати дружні стосунки,
викликати радість пізнання, виховувати прагнення до
поглиблення та удосконалення знань, вчити орієнтуватись в
нестандартних ситуаціях, впевнено себе почувати під час ЗНО .
Тип уроку: урок узагальнення і систематизації знань.
Обладнання: мультимедійний проектор, екран, комп’ютери, кейси, картки, творчі
роботи учнів (презентації).
Хід уроку
І. Вступне слово учителя, мотивація навчальної діяльності, формування
цілей та завдань уроку.
Учитель: Сьогодні ми проведемо незвичайний урок. А для цього треба
відгадати ключове слово уроку. Даю підказки…
1. З її появою математика перейшла з алгебри до математичного
аналізу…
2. Ньютон назвав її «флексією» і позначив крапкою…
3. Буває першою, другою…
4. Позначається штрихом…
Молодці! Ви правильно визначили, що мова піде про похідну, а наш урок буде проходити в незвичайній формі і буде мати назву «Свято похідної».
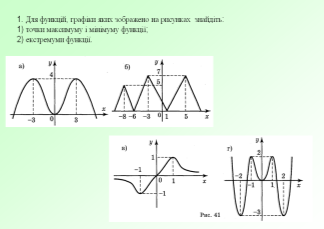
Очікувані результати :
- сформувати уміння використовувати теоретичні знання для практичного
розв’язування задач
- набути навичок творчого мислення
- набути навичок роботи в малих групах
- розвинути інформаційні і соціальні компетентності.
Пропоную епіграфом сьогоднішнього уроку вважати вислів відомого
французького математика Рене Декарта…
Недостатньо мати гарний розум,
необхідно ще вміти його
використовувати…
ІІ. Основна частина.
Учитель :У нашому житті дуже часто трапляються ситуації, коли потрібно вирішити деяке питання у найкоротший термін або з найменшими витратами, кажуть, знайти оптимальне розв'язання. Наприклад, організувати доставку товару найкоротшим шляхом або виготовити певну річ, витративши на це найменшу кількість матеріалу. Питання про знаходження оптимального розв'язання цікавило людей завжди. І при розв’язанні таких завдань на допомогу часто приходить саме похідна . Ось вам приклад з літератури.
Давайте разом пригадаємо оповідання Л. Толстого « Много ли человеку земли надо? » про селянина Пахома, який купляв землю у башкирців.
Уривок з оповідання
—А ціна яка буде? — каже Пахом.
—Ціна у нас одна: 1000 карбованців за день. (Не хрозумів Пахом.)
—Яка ж це міра — день? Скільки в ній десятин поміщається?
—Ми цього рахувати не вміємо. А ми за день продаємо; скільки обійдеш за день, те і твоє, а ціна 1000 карбованців. (Здивувався Пахом.)
—За день можна обійти багато землі. (Засміявся старшина.)
—Вся твоя, — каже. — Тільки одна умова: якщо назад не прийдеш в день до цього місця, з якого почнеш ,то пропали твої гроші.
Постановка проблеми
Яким же шляхом потрібно було йти Пахому, щоб купити найбільшу ділянку землі? На це питання ми зможемо відповісти на уроці. Для цього нам необхідно згадати усі знання та вміння по темі : « Похідна »
Робота з кейсом
Для вирішення проблеми підготовлений кейс, у якому запропоновано інформація , спираючись на яку, ви повинні вибрати найбільш вигідне вирішення поставленого завдання та обгрунтувати свій вибір.
За кілька днів учням озвучується тема наступного заняття « Екстремальні точки ». Також сказано про те, що заняття буде проводитися в режимі кейс-методу.
Сам кейс учням надається безпосередньо на занятті. На його вивчення, ознайомлення з ним відводиться близько 20 хвилин часу заняття.
Потім організовується робота в підгрупах з пошуку вирішення поставленої проблеми. Викладач консультує учнів, учні в підгрупах обговорюють варіанти, пояснюють незрозумілі моменти один одному. Цей етап заняття має тривалість близько 25 хвилин.
На наступному етапі організовується обговорення варіантів рішень підгруп, що займає близько 20 хвилин з урахуванням обговорення критеріїв ефективності пропонованих рішень.
Заключна частина заняття займає близько 25 хвилин і присвячена підбиттю підсумків, узагальненню отриманих результатів. Підсумкову частина заняття проводить викладач, спираючись на презентовані групами варіанти рішень.
Робота в групах
Для цього завдання учні поділені на групи , кожна з яких має дослідити певне питання, зашифроване у назві команди. Назву своєї групи школярі повинні відгадати за допомогою ребусів, проявивши при цьому неабияку кмітливість.
Ребуси - шифратори назв груп.
Т
+ Т
Відповідь: Зростає
4= Т
Відповідь:Критичні
Відповідь:Максимум
Відповідь:Найменше
Отож, команди носитимуть такі назви.
Група 1. Монотонність.
Група 2. Екстремуми.
Група 3. Найбільше та найменше значення функції.
Група 4. Критичні точки.
Назви команд – це частинки ( цеглинки) однієї великої теми у математиці , що носить назву « Екстремальні точки ».
Спочатку повторимо теоретичні знання по кожній частині. Учні повинні підготувати доповіді-презентації за допомогою програми Microsoft Office Power Point по темам кожної групи. Для цього вони із запропонованого кейсу вибирають саме ті теоретичні відомості та практичні завдання , які стосуються їхньої теми. Дається час на обговорення в підгрупах. У підсумку можуть бути висунуті ідеї, пропозиції щодо вирішення поставленого завдання. Питання для обговорення за матеріалами кейсів
1.Серед наведених матеріалів кейсу відшукайте ті теоритичні відомості, практичні завдання та вправи творчого характеру , що стосуються теми даної групи.
2.Обговоріть в групах результати дослідження , посортуйте їх у три папки «Теорія»,
« Практика », « Творчі вправи » та представте їх у вигляді презентації.
2. Обговорення результатів дослідження роботи в групах.
3. Спираючись на матеріали кейса і результати дослідження, кожна група виступає із пропозиціями щодо вирішення задачі.
4.Вироблення рекомендацій за результатами роботи.
5.Складання схеми розв’язання задачі на оптимізацію із життєвим навантаженням
Робота в групах відбувається за таким планом:
а) презентація, повторення алгоритму даної дії
б) практична частина ( виконання вправ)
с) сюрприз - подарунок від групи
Практичні завдання для групи « Монотонність »
Знайдіть проміжки монотонності функції:
1) ƒ(х) = х2 – 4х + 3;
2) ƒ(х) = х3 – 3х;
3) ƒ(х)=
Сюрприз-подарунок від групи « Монотонність »
Установити, про яку функцію (зростаючу чи спадну) йдеться в запропонованих вам піснях, загадках, приказках, прислів’ях:
1. Чим далі в ліс, тим більше дров.
2. Куди голка, туди й нитка.
3. Чим більше з неї береш, тим більше вона стає. (Яма)
4. Як гукнеш, так і відгукнеться.
5. Кашу маслом не зіпсуєш.
6. Менше знаєш краще спиш.
7. Жити весело – їсти нічого.
8. Тихіше їдеш – далі будеш.
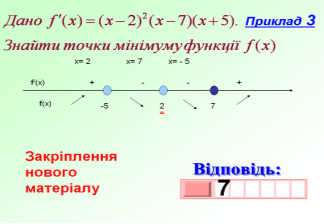
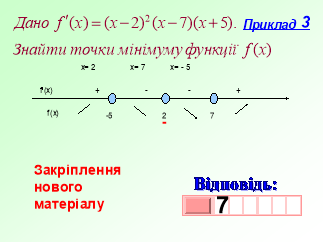
Практичні завдання для групи « Екстремуми »
Знайдіть екстремуми функції:
1) ƒ(х) = х2 – 4х +3;
2) ƒ(х) = х3 – 3х;
3) ƒ(х) = 
Сюрприз-подарунок від групи « Екстремуми »
Цього року відзначається 215 річниця народження метричної системи мір.
Вони майже однолітки з «Пригодами Мюнхгаузена». Тому наш сюрприз-подарунок пов’язаний саме з цією темою. Якщо Мюнхгаузен екзаменував нас із давніх мір, то сьогодні будемо це робити із сучасних.
Вам треба дати відповіді на запитання.
|
№з/п |
Запитання |
Правильна відповідь |
Припустима відповідь |
|
1 |
Чому дорівнює висота чотирьохповерхового будинку? |
16м |
12-20м |
|
2 |
Яка середня швидкість пішохода? |
5 км/год |
3-6 км/год |
|
3 |
Скільки важить зошит у 12 аркушів? |
35г |
20-50г |
|
4 |
Скільки важить горобець? |
60г |
30-100г |
|
5 |
Яка довжина залізничного вагона? |
23м |
18-30м |
|
6 |
Яка кількість жителів нашого міста? |
18 тис. |
15-20 тис. |
|
7 |
Скільки ударів у хвилину робить серце людини? |
70-80 |
50-100 |
|
8 |
Скільки місць в одному плацкартному залізничному вагоні? |
56 |
50-100 |
|
9 |
Скільки важить одна цеглина ? |
4 кг |
2-5 кг |
|
10 |
Скільки грамів цукру вміщає літрова банка? |
800г |
600-1000г |
Практичні завдання для групи « Найбільше і найменше значення
функції »
Знайти найбільше і найменше значення функції ƒ(х)= 1-3х2- х3 на відрізку
[-1;2]
Сюрприз-подарунок від групи « Найбільше і найменше значення функції »
Запитання: Які задачі називаються екстремальними?
Відповідь: Це задачі, які пов’язані з поняттям найбільшого, найменшого, найкращого, найоптимальнішого.
Задача: Вася має 15 гривень. Він зібрався купувати зошити по 1,5 гривні за
зошит та пограти на комп’ютері за 2 гривні. Яку найбільшу кількість
зошитів він може купити?
Практичні завдання для групи « Критичні точки »
Знайти критичні точки функції ƒ(х) = х2 + 2х .
Сюрприз-подарунок від групи « Критичні точки »
Тестове завдання на комп’ютері : графіком функції 
є:
а) пряма з виколотою точкою
б) парабола з виколотою точкою
в) гіпербола
г) коло.
Зміст кейса
Інформаційний матеріал.
|
Кросворд « Похідна » |
|
|
По горизонталі. |
|
|
1. … множник можна виносити за знак похідної. |
|
|
2. Якщо f'(x)>0 в кожній точці інтервалу І, то на цьому інтервалі функція f(x) монотонно ... |
|
|
3. Який знак кутового коефіцієнта дотичної до графіка функції, якщо відомо, що функція змінює знак з мінуса на "плюс"? |
|
|
4. Проміжки зростання і спадання функції називають проміжками … |
|
|
5. Похідна функції y=sinx в точці x=p/2 дорівнює … |
|
|
6. sinx, cosx, tgx, ctgx - це тригонометричні … |
|
|
7. Похідна функції y=x це число … |
|
|
По вертикалі. |
|
|
8. Вираз 1 /cos2x є похідною функції ... |
|
|
9. Точки, у яких функція має мінімум або максимум, називають точками ... |
|
|
10. Граничне положення січної. |
|
|
11. Значення функції в точці мінімуму. |
|
|
Розгадай кросворд |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. |
|
|
|
|
|
|
|
|
|
|
|
8. |
|
|
|
|
|
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. |
|
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
«Практика»
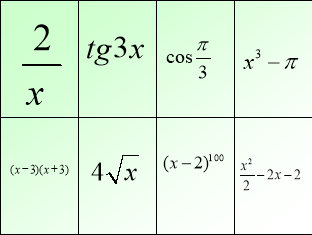
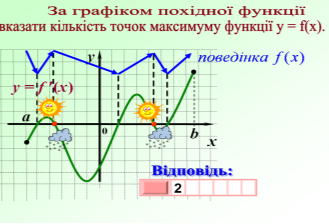
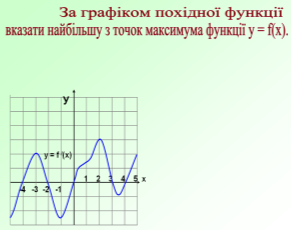
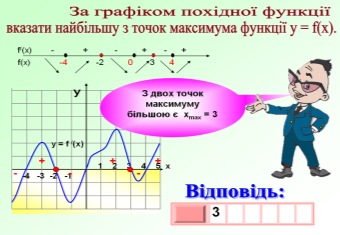
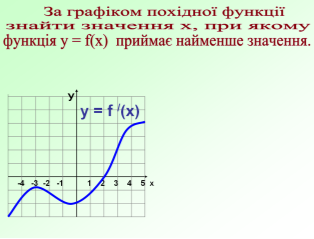
«Теорія»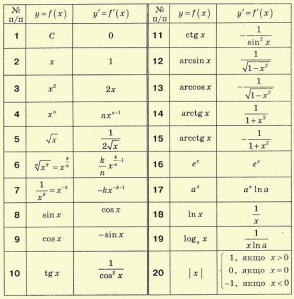 
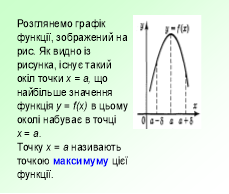
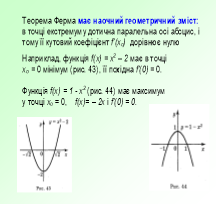
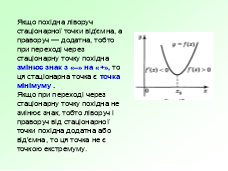
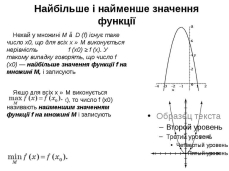
Літературна розминка
Народні прислів’я характеризують певну функцію .
Як можна назвати запропоновані функції ?
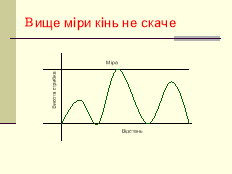
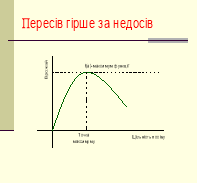
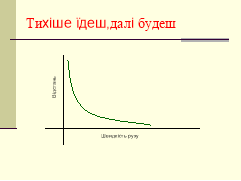
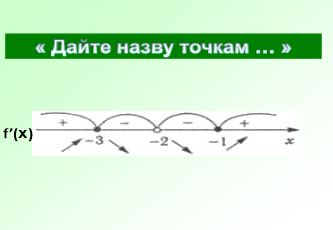
Графічний диктант « Так чи ні ? »
« Хоч слова «так» і «ні» короткі, все ж вони вимагають серйозних роздумів» - Піфагор
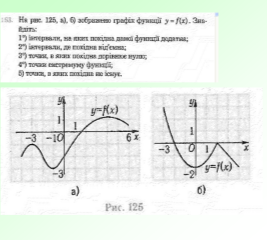
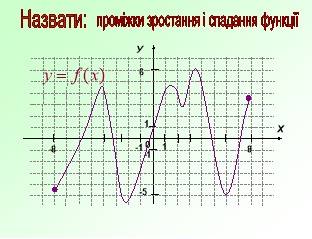
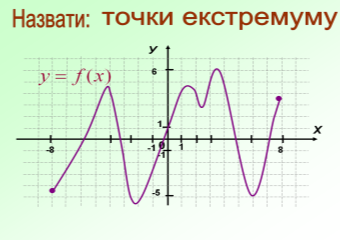
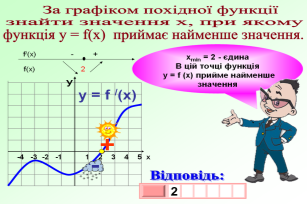
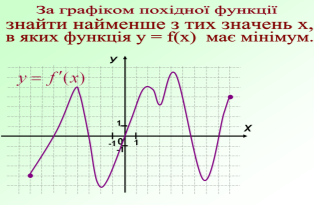
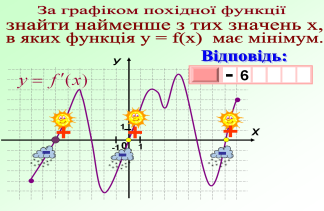
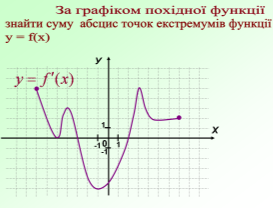
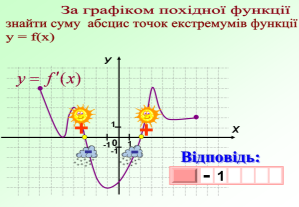
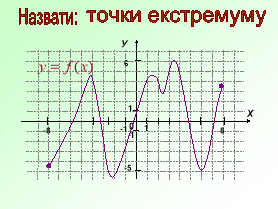
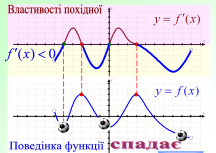
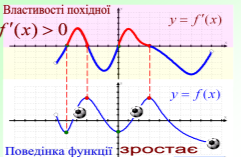
Ця робота вимагатиме від вас індивідуальних зусиль. За даним графіком визначити правильне твердження чи ні. Учні креслять трикутник з вершиною вгору , якщо твердження правильне і з вершиною вниз , якщо неправильне.
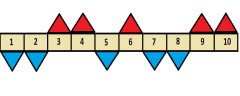
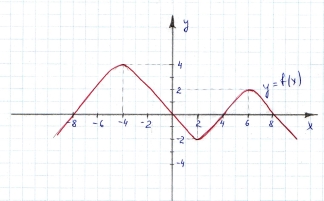
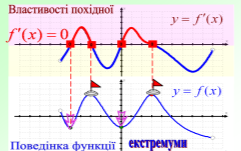
- Дана функція має дві критичні точки
- Дана функція парна
- Функція має мінімум в точці х=2
- Функція має нулі в чотирьох точках
- Функція має три максимума
- Функція зростає на проміжках [- ∞; - 4] і [2 ; 6]
- Функція спадає на проміжку [-4 ; 2]
- На проміжку (-4;2) знак похідної функції f '(x) > 0
- Екстремумами функції є значення у=4 , у=2 , у= -2
- Найменше значення функції на проміжку [-8 ; 8]
Математичне лото « Знайди пару»
Завдання «Знайди пару» Функція + похідна
|
X5 1 |
Х 2 |
2*X 3 |
1 4 |
2 5 |
|
X-3 6 |
7 |
SIN X 8 |
5*X4 9 |
-3*X-4 10 |
|
11 |
-3 12 |
-SIN X 13 |
14 |
A*X 15 |
|
A 16 |
COS X 17 |
18 |
0 19 |
12*X-5 20 |
Завдання із життєвим навантаженням
Особливий інтерес представляють задачі прикладного змісту, так звані задачі на оптимізацію, коли мова йде про дві величини, які залежать одна від одної, а саме потрібно знайти значення однієї, щоб інша була найбільшою або найменшою. Їх розв’язують за такою схемою:
1.Аналіз умови задачі
2.Створення математичної моделі
2.Одну з невідомих величин вважають незалежною і позначають х
3.Виражають у через х і записують за допомогою функції цю залежність
4.Розв’язують математичну задачу
5.Адаптовують розв’язок до основної задачі
Задачі
1.Для паркування машини відвели майданчик прямокутної форми, яка прилягає до будівлі. Майданчик обгородили металевим дротом довжиною 200м, площа майданчика при цьому виявилася найбільшою. Які розміри майданчика?
2. Рекламний білборд має форму прямокутника площею 9м2. Як його виготовити, щоб периметр був найменшим?
3. Ділянку, площею 294м2, потрібно поділити на дві рівні частини огорожею так, щоб довжина огорожі була найменшоюЗадача 1. Необхідно виготовити закритий циліндричний бак об’ємом V. Які повинні бути розміри, щоб на його виготовлення пішла найменша кількість матеріалу?
4.Вікно має форму прямокутника, завершеного півкругом. Визначити розміри вікна, щоб вікно пропускало найбільшу кількість світла, при заданому параметрі.
5.Число 20 запишіть у вигляді суми двох невід’ємних доданків так, щоб добуток їхніх квадратів був найбільшим.
6.Число 36 запишіть у вигляді добутку двох додатних чисел, сума яких найменша.
7.Знайдіть додатне число, потроєний квадратний корінь якого більше цього числа на найбільше значення.
8.Серед прямокутників, що мають периметр 20см, знайдіть той, діагональ якого найменша.
9.Із усіх прямокутників, площа яких дорівнює 9см2 , знайдіть прямокутник з найменшим периметром.
10.Парканом довжиною 80м треба огородити прямокутну ділянку найбільшої площі. Знайдіть розміри ділянки.
11. Із квадратного листа жерсті з стороною а необхідно виготовити відкриту зверху коробку, вирізавши по кутам квадратики та загнувши утворені кромки. Яка повинна бути сторона коробки, щоб її об’єм був найбільший.
12. На сторінці текст повинен займати 
. Верхнє та нижнє поля повинні бути 3 см, праве та ліве –
по 2 см. Якщо приймати до уваги тільки економію паперу, то які повинні бути найвигідніші розміри сторінки.
Складаємо алгоритм заходження …
ІІІ. Завдання у форматі ЗНО:
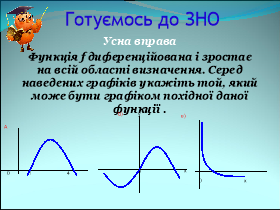
1. Функція f(х) має в точці х0 похідну f'(х0 ) = - 4. Визначте значення похідної функції g(х) = 2•f(х) + 7х - 3 в точці х0 .
|
А |
Б |
В |
Г |
Д |
|
-1 |
-4 |
-8 |
15 |
12 |
2. Установіть відповідність між формулами (1-4) і значеннями їхніх похідних
у точках х0 ( А – Д ).
|
Функція, точка |
Значення похідної функції у точці |
|||||
|
1. у = |
А -2 |
|||||
|
2. у = 2 cosх, х0 = |
Б 2 |
|||||
|
3. у = 2х3 - |
В -1 |
|||||
|
4. у = 2 |
Г 0 |
|||||
|
|
Д 3 |
|||||
|
|
А |
Б |
В |
Г |
Д |
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
х
-
, х
ІV. Самостійна робота на 4 варіанта.Тестові завдання.
|
В -1 |
В-2 |
В-3 |
В-4 |
|
Знайти проміжки монотонності функції: |
|||
|
у = -х2 + 2х - 3 |
у = х2 – 2х + 3 |
у = 3х2 – 6х + 7 |
у = -3х2 + 6х + 3 |
|
Знайти екстремуми функції: |
|||
|
у = х3 – 6х2 |
у = 2х3 – 3х2 |
у = 2х2 - |
у = |
|
Знайти найбільше і найменше значення функції: |
|||
|
у = х + |
у = - |
у = |
у= х - |
|
Записати рівняння дотичної до графіка функції у точці х0 : |
|||
|
у = х3+ х2, х0 =1 |
у = х3- х2, х0 = -1 |
у= 12х –х3, х0=1 |
у = х3 – 6х2, х0 = -1 |
|
Дослідити за схемою та побудувати графік функції: |
|||
|
у = х3 – 3х |
у = 3х – х3 |
y = x4 – 4x2 |
у = х4 – 4х3 |
х
х
- х
х
хЗадача про Пахома
А тепер повернемося до задачі про селянина Пахома.
Нехай швидкість руху чоловіка 5 км/год. І він може безперервно рухатись 8 годин. Отже, за день він може пройти 40 км. Ділянка для зручного ведення господарства повинна мати форму прямокутника. Складемо математичну модель цієї задачі.
Периметр прямокутника дорівнює 40 км. Якими мають бути розміри цього прямокутника, щоб його площа набувала найбільшого можливого значення?
Позначимо одну сторону прямокутника х, тоді друга буде 20-х, площа прямокутника дорівнює х(20-х). З умови задачі випливає, що 
. Таким чином, задача звелася до знаходження найбільшого значення функції f(х)=20х-х2на відрізку [0; 20].
1.Знайдемо похідну:
f'(х)=20-2х.
2.Знайдемо критичні точки:
20-2х=0;
х=10.
Точок, в яких похідна не існує, немає.
Точка х=0 належить проміжку [0; 20].
3.Знайдемо значення функції у критичній точці і на кінцях відрізка:
f(0)=0;
f(20)=0;
f(10)=100.
Звідси отримуємо, що функція f(х)=20х-х2на інтервалі (0; 20) набуває найбільшого значення при х=10.
Таким чином, із усіх прямокутників із периметром 40 км найбільшу площу має квадрат.
Відповідь: квадрат зі стороною 10 км.
V. Підведення підсумків уроку. Оцінювання учнів. Рефлексія.
Учитель. Похідна – це фундаментальне поняття математичного аналізу ,
за допомогою якого досліджують процеси і явища в природних,
соціальних і економічних науках. Тому вивченню цієї теми ми
приділили особливу увагу.
Сьогодні ми повторили матеріал по темі «Екстремальні точки» , виконали типові вправи, склали алгоритми знаходження критичних точок, екстремумів, Проміжків монотонності , найбільшого та найменшого значень функції, з’ясували , що багато життєвих задач можна розв’язати за допомогою похідної .Я надіюсь, що усі ці знання та вміння стануть у пригоді вам при підготовці до ЗНО.
Я переконалась, що ви – клас однодумців, які вміють застосовувати набуті знання. Думаю, що уміння аналізувати ситуацію ще не раз стане вам у нагоді. Пам’ятайте, що математика це ланцюг понять: випаде одна ланка і незрозуміле буде наступне. Тож тренуйте свій розум і тоді дорогу до успіху буде для вас відкрито!
Рефлексія
VI. Домашнє завдання.
Складіть схему для розв’язування кожного завдання і представте її для всього класу у формі презентації.
Завдання 1. Знайти різницю найбільшого та найменшого значення функції: f(x)= x2 + (16-x)2 на [8;16]
Завдання 2. Рекламний білборд має форму прямокутника площею 9м2. Як його виготовити, щоб периметр був найменшим?
Завдання 3. Ділянку, площею 294м2, потрібно поділити на дві рівні частини огорожею так, щоб довжина огорожі була найменшою.
Дайте відповіді на запитання :
- Яка з запропонованих задач є найлегшою?
- Що спільного у схемах розв’язання задач?
- Який етап у розв’язанні цих задач є основним, на Вашу думку?
За даними схемами розв’язку Ви зможете розв’язати ці задачі вдома і на наступному уроці ознайомити усіх з результатами своєї роботи.
про публікацію авторської розробки
Додати розробку