Обчислення площ плоских фігур

 

 

 

 

 

 

Урок алгебри і початків

аналізу в 11 класі

 

 

 

 

 

 

 

 

 

Підготувала: вчитель математики
Скала-Подільської ЗОШ І-ІІІ ступенів

Войцехівський В.Р.

 

 

 

 

 

 

 

 

 

 

Скала–Подільська

2018
Тема уроку: Розв'язування вправ на обчислення площ плоских фігур за допомогою інтеграла.

Мета уроку: розвивати практичні навички розв’язування вправ на обчислення площ плоских фігур за допомогою інтеграла, формування основ логічного мислення.

Обладнання: Інтерактивна дошка, проектор, роздатковий матеріал.

Хід уроку

І. Актуалізація опорних знань.

Малюнок на екрані: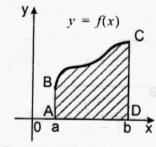

 

1. Як називається геометрична фігура ABCD?
2. Яка фігура називається криволінійною трапецією?
3. Як обчислити її площу?

 

Сформулювати загальні властивості площ плоских фігур.

Площа – це додатна величина, числове значення якої має такі властивості:

1) Рівні фігури мають рівні площі;

2) Якщо фігура розбивається не частини, що є простими фігурами то площа цієї фігури дорівнює сумі площ її частин.

3) Площа квадрата із стороною, що дорівнює одиниці вимірювання дорівнює 1 кв.од.

Малюнок на екрані:

Як обчислити площу даної  фігури?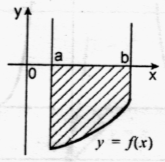

 

 

 

 

 

 

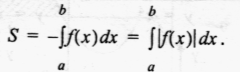
Малюнок на екрані:

Обчислити площу даної фігури.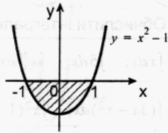

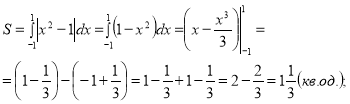
Малюнок на екрані:

Як обчислити площу даної  фігури?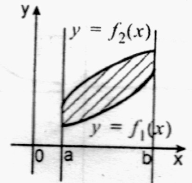

 

 

 

 

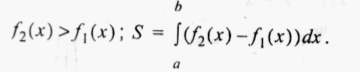
Малюнок на екрані:

Обчислити площу даної фігури.

 

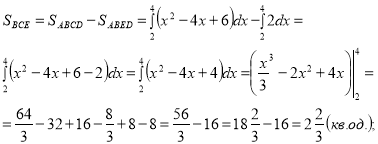
Малюнок на екрані: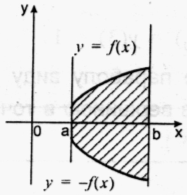

Як обчислити площу даної  фігури?

 

 

 

 

 

 

 

 

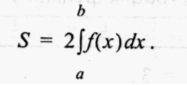
Малюнок на екрані:

Обчислити площу даної фігури.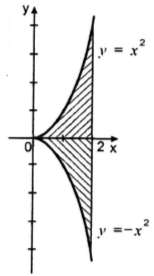

 

 

 

 

 

 

 

 

 

 

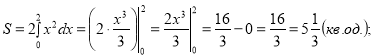
Малюнок на екрані:

Як обчислити площу даної  фігури?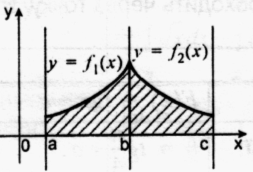

 

 

 

 

 

 

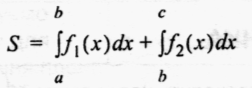
Малюнок на екрані:

Обчислити площу даної фігури.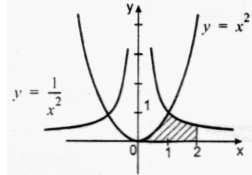

 

 

 

 

 

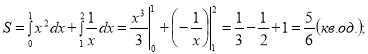
Малюнок на екрані:

Як обчислити площу даної  фігури?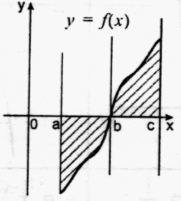

 

 

 

 

 

 

 

 

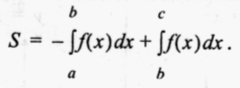
Малюнок на екрані:

Обчислити площу даної фігури.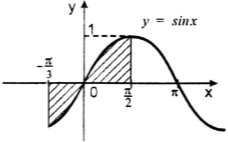

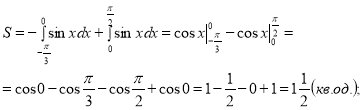
Індивідуальні завдання для учнів з високим рівнем підготовки.

№1

1. Обчислити площу фігури, обмеженої параболою і прямою

Відповідь:

2. Знайти площу фігури, обмеженої параболою , дотичною проведеною до даної параболи в точці з абсцисою та віссю ординат.

Відповідь:

№2

1. Обчислити площу фігури, обмеженої параболою і прямою

Відповідь:

2. Знайти площу фігури, обмеженої параболою , дотичною проведеною до даної параболи в точці з абсцисою та віссю ординат.

Відповідь:

 

ІІ. Розв’язування вправ

1. Обчислити площу фігури обмеженої лініями:

а)

Розв’язання: (коментовано і з записами розв'язку на дошці і в зошитах).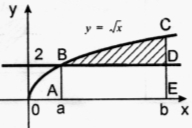

З'ясуємо алгоритм розв’язування вправи:

1. Будуємо графік заданої функції та відмічаємо фігуру, площу якої треба знайти.

 

2. Запишемо формулу для обчислення площі шуканої фігури:

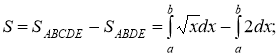
3. Знаходимо межі інтегрування:

4. Обчислюємо шукану площу за формулою:

Відповідь:

б)

1. Будуємо графік заданої функції та відмічаємо фігуру, площу якої треба знайти.

2. Запишемо формулу для обчислення площі шуканої фігури:

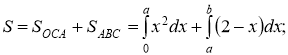
3. Знаходимо межі інтегрування: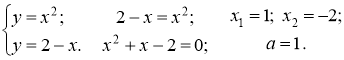  

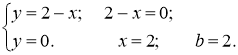
4. Обчислюємо шукану площу за формулою:

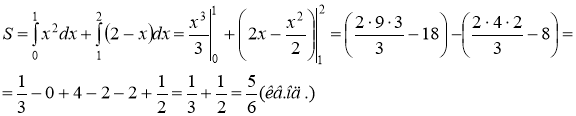
Відповідь:

2. Використовуючи геометричний зміст інтеграла обчислити: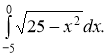

Розглянемо функцію ; Знайдемо її область визначення:

Отже на відрізку [0;5] функція визначена і набуває невід'ємних значень.

Тому значення інтеграла дорівнює площі фігури обмеженої лініями , у=0; у=–5; х=0.

Якщо – рівняння півкола з центром у точці О(0;0) та радіусом 5.

 

 

 

Відповідь:

3. Накреслити фігуру, площа якої дорівнює такому інтегралу:

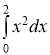а) ; б) ; в) .

ІІІ. Домашнє завдання.

№64 (7, 8) ст. 149.

IV. Підсумок уроку. Оцінювання.

 

Покликання на презентацію:

https://drive.google.com/drive/folders/1zbghxe_hzYx5suOPaX2cmUOys0L-deHq?usp=sharing