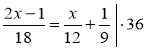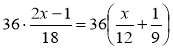Лінійне рівняння з однією змінною
Тема. Лінійне рівняння з однією змінною
Мета: повторити, поглибити та розширити знання учнів про види рівнянь з однією змінною, що зводяться до лінійних рівнянь з однією Змінною (рівняння з модулем та рівняння, що містять дроби), та способи рівносильних перетворень таких рівнянь.
Тип уроку: поглиблення знань, засвоєння вмінь.
Хід уроку
I. Організаційний момент
II. Перевірка домашнього завдання
Оскільки метою виконання домашнього завдання було формування сталих навичок розв'язування лінійних рівнянь ах = b з однією змінною при різних значеннях а і b, то № 1 і 2 слід ретельно перевірити й ще раз прокоментувати спосіб розв'язування рівнянь.
№ 1. Розв'яжіть рівняння:
|
1) 15(х + 2) – 30 = 12х 15x + 30 – 30 = 12x 15x = 12х 15x – 12x = 0 3x = 0 х = 0 |
2) 6(1 + 5х) = 5(1 + 6х) 6 + 30x = 5 + 30x 30x – 30x = 5 – 6 0x = -1 коренів немає |
3)3у + (у–2) = 2(2у–1) 3у + у – 2 = 4у – 2 4у – 2 = 4у – 2 4у – 4у = -2 + 2 0y = 0 у — будь-яке число |
4) 6у – (у – 1) = 4 + 5у 6у – у + 1 = 4 + 5у 5у + 1 = 4 + 5у 5у – 5у = 4 - 1 0у = 3 коренів немає |
№ 2. Відшукайте корені рівнянь:
|
1) 7(х – 8,2) = 3x + 19 7x – 57,4 = 3x + 19 7x – 3x = 19 + 57,4 4х = 76,4 х = 76,4 : 4 x = 19,1 |
2) 0,2(5x – 6) + 4x = 3,8 x – 1,2 + 4x = 3,8 5х – 1,2 = 3,8 5х = 3,8 + 1,2 5x = 5 x = 5 : 5 x = 1 |
3) 0,4(2x – 7) + 1,2(3x + 0,7) = 1,6x 0,8x – 2,8 + 3,6x + 8,4 = 1,6x 4,4x + 5,6 = 1,6x 4,4x – 1,6x = -5,6 2,8x = -5,6 x = -5,6 : 2,8 x = -2 |
III. Актуалізація опорних знань
Під час математичного диктанту повторюємо теоретичний матеріал та способи дій, розглянуті на попередньому уроці.
Математичний диктант
- Придумайте і запишіть будь-яке лінійне рівняння з одним невідомим х [у].
- Як називається рівняння -2х = 17 [17х = -2]?
-
За яких умов рівняння ах = 5 [ау = 3] має єдиний корінь (не має коренів)?
Запишіть цей корінь. - Розв'яжіть рівняння 0,2х = -1 [-0,3х = 1].
- Розв'яжіть рівняння 2х + 1 = 3х – x [х + 3 = 5 + х – 2].
- Розв'яжіть рівняння 5 – х = 2x + 2 [2 – 2х = -2х + 3].
По завершенні роботи відповіді перевіряються, корегуються і повторюються означення лінійного рівняння з однією змінною та схема розв'язання лінійних рівнянь.
IV. Систематизація, поглиблення та розширення знань
- Робота з випереджальним завданням
Розгляньте рівняння: | х | = 3; | х | =0; | х | = -3.
За відомим алгоритмом виконайте порівняння (додаток 2).
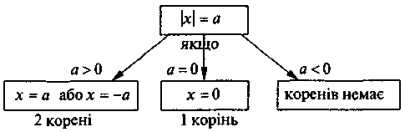
Висновки: 1) Усі наведені рівняння можна записати у вигляді одного рівняння | х | = а, де а — будь-яке число.
2) Спосіб розв'язання і кількість коренів цього рівняння залежить від знака числа а, а саме:
- Розширення знань
Як було вже сказано на попередньому уроці, розв'язання багатьох рівнянь, що мають одну змінну, зводиться до розв'язування лінійних рівнянь з однією змінною. Серед таких рівнянь можна виділити:
а) рівняння з модулем;
б) рівняння, що містять дроби.
Далі розбираємо розв'язання рівнянь названих видів.
|
а) Перш ніж починати пояснення, слід активізувати мислення учнів, запропонувавши порівняти рівняння з рівнянням виду | х | = а. Чим відрізняється дане рівняння від рівняння | х | = а? Чим схожі ці рівняння? Чим схожий спосіб розв'язання (перший крок) і чим буде відрізнятися розв'язання?
Після цього робимо записи в зошитах (проводимо усні зауваження): 1) 2x – 3 = 3 або 2) 2x – 3 = -3. (Оскільки 3 > 0, | x | = а, а > 0, то x = а або x = -а. Розв'язуємо лінійні рівняння.) 2х = 6, 2х = 0. х = 3, х = 0. Відповідь. 3; 0 |
б) Перш ніж розв'язувати рівняння, слід порівняти його з іншими рівняннями, що були розв'язані раніше. Провести бесіду, розглянувши такі питання: Чим відрізняється дане рівняння від рівняння № 1 в домашньому завданні? Що спільного? Яку властивість рівносильних рівнянь можна використати, щоб позбутися дробів? Яка властивість дробів використовується при цьому? Після цього можна записати розв'язання, додавши усні коментарі.
(Знайдемо НСК (18; 12; 9) = 36 та помножимо на нього обидві частини рівняння.) |
|
(Виконаємо множення.)
2(2х – 1) = 3х + 4х; 4х – 2 = 3х + 4. (Виконаємо рівносильні перетворення, зведемо рівняння до лінійного і розв'яжемо його.) 4х – 3х = 4 + 2, х = 6 Відповідь. 6 |
Висновки. Розібравши приклади а) та б) ми впевнилися в тому, що деякі рівняння з модулем, так само як і деякі рівняння з дробами (не всі!!!), шляхом виконання рівносильних перетворень та використання властивостей чисел можуть бути зведеш до лінійних рівнянь з однією змінною.
V. Засвоєння вмінь
Виконання письмових вправ
-
Розв'яжіть рівняння, що містять змінну під знаком модуля:
1) |х| = 3; 2) |х| + 1 = 7; 3) |х| - 2 = -3; 4) |х – 3| = 2; 5) |х – 4| = 0;
6) |х + 3| = -4; 7) 3|x| - 1 = 0; 8) |3х + 2| - 4 = 0; 9) |2(x – 3)(х + 4)| = 2. - Розв'яжіть рівняння:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
;
4) ![]() ; 5)
; 5) ![]() .
.
- * Логічна вправа.
Знайдіть пропущений рисунок:
|
|
|
|
3х – 8 = 8x – 28 |
? |
VI. Підсумки уроку. Рефлексія
Ігровий момент «Знайдіть помилку»
Учень 7 класу Петрик Тяпляпкін сказав, що дуже добре навчився розв'язувати рівняння, що зводяться до лінійних, і показав, як він розв'язує рівняння. Ось його розв'язання.
|
а) х – 2х = -1 + 3, -x = 2, х = -2 |
б) |х – 3| = 2, х – 3 = 2, х = 5 |
Чи згодні ви з такими розв'язаннями? Як би ви оцінили успіхи Петрика?
VII. Домашнє завдання
№ 1. Розв'яжіть рівняння:
1) |2х - 3| = 5; 2) |2х – 1| + 7 = 8; 3) |5х – 4(2х + 3) | = 6;
4)* (випереджальне домашнє завдання) 2(|x| - 3) – 4(2|х| + 9) = -48;
5) ![]() ; 6)
; 6) ![]() .
.
№ 2. При якому значенні а рівняння ах = 42:
1) має корінь -7; 2) коренів не має; 3) має безліч коренів?


про публікацію авторської розробки
Додати розробку