М.В.Наумова "Множини. Графи. Алгебра логіки. "
«Математика є спосіб називати різні речі одним ім'ям»,-
так одного разу сказав Пуассон. А ще він відзначав, що: «Ця наука, що поєднує точність математичних доказів з невизначеністю випадку, ці, здавалося б, суперечливі елементи, з повним правом може претендувати на титул - Математики випадкового».
М.В.Наумова


Розділ 1. Множини.
1.1.Множини. Елементи множини.
 «Математика є спосіб називати різні речі одним ім’ям»,-
«Математика є спосіб називати різні речі одним ім’ям»,-
так одного разу сказав Пуассон. А ще він відзначав, що: «Ця наука, що поєднує точність математичних доказів з невизначеністю випадку, ці, здавалося б, суперечливі елементи, з повним правом може претендувати на титул - Математики випадкового».
Давайте поміркуємо над тим, як людина, спрощуючи, ускладнює собі життя. Ось, наприклад, хтось сказав, звернувшись, до лікаря: « Мене вкусила комаха». І, що станеться, лікар змушений буде задавати питання, щоб з'ясувати яка саме комаха вкусила, щоб призначити правильне лікування. А ось ще приклад: «Я навчився грати в спортивну гру». Знову теж саме - ми починаємо вгадувати в яку саме гру тепер ти можеш грати. Добре, що спортивних ігор або комах не так багато, а якщо хтось скаже: « Я задумав число». То, що ж прийдеться тепер все життя перелічувати числа? Що ж тут відбувається? А нічого особливого, просто кожна із цих людин називає різні предмети одним загальним для них словом. У математиці набір предметів або понять, зібраних за будь-якою ознакою, називають множинами, а кожний із цих предметів- елемент множини.
Поняття множина, подібно поняттям точки, числа, прямої і т.д., не зводиться до інших понять математики й, тому строго визначення немає. Можна сказати, що множина - це «сукупність», «набір», «ансамбль», «колекція», «клас» і т.д. Але все це не є математичним визначенням. Для того, щоб зрозуміти, що таке множина, наведемо приклади.
![]() Ми маємо право казати про множину всіх піщин у пісочних годинниках,
Ми маємо право казати про множину всіх піщин у пісочних годинниках,
про множену всіх квітів у вазі, про множину всіх зірок на небі, про
множину всіх тварин на Землі, про множину атомів на Сонце й т.д. У звичайному житті, правда не кажуть множина корів, а скажуть просто череда, не множина коней - а табун, не множина учнів - а клас. Дуже важливо завжди визначити ознаку, за якою об'єкти поєднуються в ту або іншу множину, який елемент буде входить до даної множини, кажуть «належати множині», а який ні. Наприклад, розглянемо множину учнів 6-А класу. Чи є елементом цієї множини дошка? парта? портфель? конкретний учень Петро Васечкин? А чи є така множина, що містить всі перераховані елементи? Так, - це множина «класна кімната».
 Усі елементи цієї множини можна перерахувати,
Усі елементи цієї множини можна перерахувати,
іншими словами, кожному елементу
можна присвоїти його порядковий номер,
або перенумерувати.
![]()
![]() Такі множини називають рахунковими.
Такі множини називають рахунковими.
 Множини можуть мати скінченне число елементів – скінченна
Множини можуть мати скінченне число елементів – скінченна
![]()
![]() множина. Наприклад, множина всіх цифр. Ця множина має
множина. Наприклад, множина всіх цифр. Ця множина має
10 елементів: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
![]() Множини можуть мати нескінченне число елементів –
Множини можуть мати нескінченне число елементів –
нескінченні множини. Наприклад, множина всіх натуральних чисел.
Нескінченна множина називається рахунковою, якщо ії елементи можна
занумерувати натуральними номерами.
Якщо елементи нескінченної множини перенумерувати не можна, то вона незлічена.
Множина, що не має жодного елемента, називається порожньою множиною - ![]() .
.
Позначають множини великими латинськими літерами. Наприклад, множина всіх цифр А={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Елементи множини прийнято позначати малими латинськими літерами. Наприклад, а є А. Знак «є» позначає, що елемент а належність даній множині, читають: « елемент а належить множині А». Знак «![]() » позначає «не належить множині», наприклад, а
» позначає «не належить множині», наприклад, а![]() А. Читають: «елемент а не належить множині А». Який із цих двох значків ти поставиш замість
А. Читають: «елемент а не належить множині А». Який із цих двох значків ти поставиш замість ![]() у таких прикладах:
у таких прикладах:
Риба ![]() множина тварин, що видають звуки;
множина тварин, що видають звуки;
Чорнило ![]() множина напоїв;
множина напоїв;
Август ![]() множина римських імператорів;
множина римських імператорів;
Дніпро ![]() множина українських річок;
множина українських річок;
Математика ![]() множина улюблених предметів.
множина улюблених предметів.
Деякі множини мають давно визначені для них позначення, наприклад, множину натуральних чисел прийнято позначати N, множину цілих чисел - Z, множину раціональних чисел - Q.
Дуже часто множини зображують за допомогою діаграми Венна.

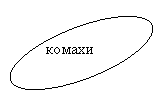

![]()
 1.2. Підмножина. Об'єднання множин.
1.2. Підмножина. Об'єднання множин.
Переріз множин. Доповнення множини.
Ми знаємо, що предмети і явища навколишнього світу не існують незалежно друг від друга, вони взаємозалежні одне від одного.
Такі ж зв'язки існують і між множинами.
Кожний клас є частиною школи, родина є частиною роду, множина прямокутників є частиною множини всіх чотирикутників.
Тоді, якщо множина А={1,3,5,7,9,11,13,15}, а множина В={1,3,5,7}, то множина В є частиною множини А. Але, адже як сказав Пуассон:«Математика є спосіб називати різні речі одним ім'ям”. І для цього в математиці є своя назва. Множину В називають підмножиною множини А. Тобто: якщо кожний елемент множини В є також елементом множини А , то множина В називається підмножиною множини А.
Однак учені – народ ледачий, вони увесь час намагаються полегшити собі життя. Замість того, щоб казати, що В є підмножиною А, або міститься в А, вони кажуть «В підмножина А», а пишуть ще коротше: В![]() А.
А.
Отут навіть граматичних помилок не наробиш. Погодься, що значки ![]() й
й ![]() схожі. Напевно, якщо є
схожі. Напевно, якщо є ![]() , то можна придумати значок і для випадку: В не є підмножиною множини А, щоб знову не витрачати багато часу на запис. Спробуй це зробити сам._____________________
, то можна придумати значок і для випадку: В не є підмножиною множини А, щоб знову не витрачати багато часу на запис. Спробуй це зробити сам._____________________
Як ти думаєш, що вийде, якщо взяти підручники по математиці, додати до них підручники по історії, до них додати підручники по літературі, до них додати підручники по іноземній мові, що вивчають у твоїй школі, до них додати ще всі інші підручники й об'єднати все це в одному приміщенні? Правильно, одержимо шкільну бібліотеку - об'єднання всіх шкільних підручників. Так роблять і з множинами.
Якщо є А={1,3,5,7,9,11} і В={2,4,6,8,10,12}, то С={1,2,3,4,5,6,7,8,9,10,11,12} - об'єднання множин А и В.
Об'єднанням (сумою) множин А і В називають таку множину С, яка містить у собі всі елементи множини А і ті елементи множини В, яких немає у множині А.
Позначають об'єднання значком ![]() .
.
Тому С=А ![]() В або С=А+В.
В або С=А+В.
Це можна зобразити за допомогою діаграми Венна.


![]()
А а В С=А![]() В
В
с



![]() А В С=А
А В С=А![]() В А
В А
В
Твої однокласники ![]() твої однокласниці
твої однокласниці![]() ти = твій клас.
ти = твій клас.
![]()
![]()
![]()
![]()
![]() =
=
Розглянемо множину А={1,2,3,5,7,8,9} і множину В={1,2,4,5,6,10}. У них є однакові елементи або спільні елементи 1,2,5. Ці елементи складають множину С, яку називають перерізом множин А и В.
Перерізом (добутком) множин А и В називають така множина С, яка складається лише зі спільних елементів множин А и В.
Позначають переріз значком ![]() .
.
Тобто С=А![]() В або С=А.В.
В або С=А.В.
На діаграмі Венна це виглядає так:


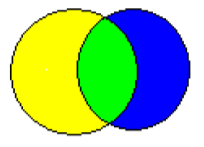 C=A
C=A![]() B
B
А а b У C={a,b,c,d}.
с d
Доповненням множини А до множини В називають така множина С, для якої виконуються умови: 1) А![]() С=В; 2) A
С=В; 2) A![]() С=
С=![]() .
.
На діаграмі Венна це виглядає так:

 У З
У З
А

1.3.Задачі й питання.
№1.
Запишіть множину, елементами якої будуть літери слова:
математика; алгебра; електрика.
№2.
Елементами яких множин можуть бути вуглець, кисень, водень?
№3.
Поєднаєте перечислені предмети в кілька множин: олівець, лялька, лінійка, зошит, зубна щітка, мило, м'ячик, тапочки, плюшеве ведмежа, морозиво, цукерка, годинник, чашка, ковбаса, скакалка, сорочка, кубики, огірок, бутерброд, ложка, ніж, виделка, тістечко, помідор, капелюх, кепка, яблуко, піна, персик, підручник, циркуль, перець, плаття, санки, лижи, ковзани, буряк, груша, сік, окуляри, рушник, чайник, цукор, чай.
№4.
Які з даних множин є рахунковими, а які незліченними?
- множина всіх відрізків довжиною від 5 до 10 див;
- множина всіх цілих чисел, кратних 7;
- множина всіх крапок на окружності;
- множина всіх крапок усередині кола?
№5.
Наведіть приклади порожніх множин.
№6.
Прочитайте казку Г. Остера «Пампукская хрюря». Намалюйте діаграму Венна і запишіть множину, про яку йде мова.
«Якось одного разу Слоненя, Удав і Мавпа сиділи й розмовляли. Раптом прилетів Папуга й запитав:
- Ви знаєте, що таке кукаляка?
- Ні, не знаємо,- відповіло Слоненя.
- Кукаляка, - важливо сказав Папуга, - це така скринька, у якому лежить мукука.
- А що таке мукука?- запитала Мавпочка.
- Мукука - це така коробочка, у якій лежить бисяка,- відповів Папуга.
- А бисяка, що таке?- зачудувався Удав.
- Бисяка - це шухлядка, у якому лежить хрюря,- сказав Папуга. Подумав і додав: « Папукская хрюря».
- Що це за пампукская хрюря?- обурився Удав.- Ніяких пампукских хрюрей я ніколи не бачив!
-Пампукская хрюря - це такий пакетик, у якому лежить мамурик.
-Зрозуміло,- сказало Слоненя,- мамурик - це, напевно, теж яка-небудь шухлядка, у якому лежить ще що-небудь. Ну, а все-таки, що ж там у самій середині цих шухлядок, коробок і пакетиків? Скажи, будь ласка, Папуга.
- А хіба це так важливо? - відповів Папуга й полетів».
№7.
Для яких пар множин має місце одна із відносин: В![]() А, А
А, А![]() В, А=В:
В, А=В:
1)A={a,b,c,d}, B={a,b,d};
2)A={a,b,c}, B=![]() ;
;
3)A={a,b,c}, B={b,c,a};
4)A={1,2,3,4,5,6}, B={2,4,6,7,8,9}.
№8.
Запишіть всі підмножини таких множин:
1)С={m,n,f};
2)D={1,a,3,c,4,t};
3)S={1,2,3,4,5};
4) T={![]() }.
}.
№9.
За даною ознакою, запишіть множини:
- всіх цілих чисел, більших 20 і менших 70, кратних 5;
- всіх голосних літер українського алфавіту;
- всіх літніх місяців;
- всіх імен однокласників, що починаються на букву А.
№10.
Нехай А - множина, що складається з 8 учнів, які займаються в математичному кружку, а В - множина всіх учнів класу. Запишіть відношення, що зв'язують ці множини й намалюйте діаграму Венна.
№11.
Намалюйте діаграму Венна для наступних пар множин:
1)A={a,b,c,d}, B={a,n,d,t};
2)A={a,b,c}, B={1,2,3,4};
3)A={a,b,c}, B={b,c,a};
4)A={1,2,3,4,5,6}, B={2,4,6,7,8,9}.
№12.
Нехай множина А={{1,2,3},{1,3},1,2}. Чи справедливо відношення:
1) {1,2}![]() А; 2) {1,2}
А; 2) {1,2}![]() А;
А;
3) {1,3}![]() А; 4) {1,3}
А; 4) {1,3}![]() А?
А?
№13.
Знайти переріз наступних множин:
1)A={a,b,c,d}, B={n,t,f,g};
2)A={2,4,6,7}, B={1,2,3,4};
3)A={a,b,c}, B={b,c,a};
4)A={1,a,3,c,5,t}, B={2,a,3,5,9}.
№14.
Знайти об'єднання наступних множин:
1)A={a,b,c,d,n}, B={a,n,d,t};
2)A={a,b,c}, B={1,2,3,4};
3)A={1,2,3,4,5,6}, B={2,4,6,7,8,9}.
№15.
Дано множини А и В, знайти об'єднання й переріз цих множин, якщо:
1)А - множина чисел кратних 5 і менших 100, В - множину чисел менших 105 і кратних 7;
2) А - множина чисел кратних 2 і менших 65, В - множину чисел менших 65 і кратних 3.
 Розділ 2.Графи
Розділ 2.Графи
1.Вступ.
Дорогі діти, ми з вами незабаром почнемо (а деякі вже почали) вивчати такий предмет, як геометрія. Але насправді, ви знайомі з нею із самого народження, все, так чи інакше, відноситься до геометрії, ніщо не випадає з під її уважного погляду.
«Я думаю, що ніколи, дотепер, ми не жили в такий геометричний період. Всі навколо - геометрія». Ці слова, сказані великим французьким архітектором Ле Корбюзье на початку ХХ століття, дуже точно характеризують і наш час. Мир, у якому ми живемо, наповнений геометрією будинків і вулиць, гір і полів, творіннями природи й людини. Краще орієнтуватися в цьому всесвіті, відкривати нове, розуміти красу й мудрість навколишнього світу допоможе нам тема «Графи».
У геометрії цей розділ називається топологія - самий «молодий» розділ геометрії.
Щоб одержати деяке уявлення про топологію проведемо такий дослід з аркушем паперу.
Візьмемо смужку кольорового паперу.
![]() A B
A B
D C
![]() D C
D C
A B
 Зігнемо й склеїмо його так, щоб збіглися кінці D і B, A і C.
Зігнемо й склеїмо його так, щоб збіглися кінці D і B, A і C.
А З
D B
Якщо тепер ми проведемо олівцем лінію по отриманій фігурі, починаючи від місця склеювання, то виявиться, що ця лінія пройде по смужці паперу із двох її сторін. Така фігура називається лист Мебіуса. Він один з об'єктів вивчення топології. Цікаво, що з погляду топології гайка, макаронина й кухоль - однакові об'єкти. Їх ріднить те, що кожний з них має один й тільки один отвір - «топологічні родичі».
Серед букв російського алфавіту теж є топологічно однакові букви. Уявіть собі, що вони зроблені з м'якого дроту. Які з букв можна перетворити одну в іншу, якщо не розривати дріт у місцях з'єднань і не склеювати кінці? Дріт можна тільки гнути й розтягувати.
- Г ; Л ; М ; П ; С;
- Е ; В; Т ; Ч.

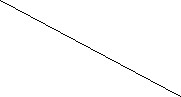
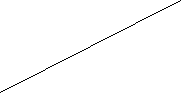 Особливим інтересом користуються задачі на малювання фігур одним розчерком. Спробуй намалювати запропоновані фігури, не відриваючи олівець від паперу.
Особливим інтересом користуються задачі на малювання фігур одним розчерком. Спробуй намалювати запропоновані фігури, не відриваючи олівець від паперу.



![]()
![]()






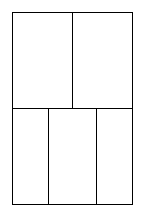


Звичайно, усі полюбляють малювати. Легко намалювати коло, не відриваючи олівець від паперу й не проводячи двічі ніяку лінію. Ну, а із цими фігурами впоралися? З усіма?

2.Поняття графа. Нуль-граф. Повний граф.
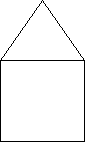 Легко намалювати коло, не відриваючи олівець від паперу й не проводячи двічі ніяку лінію. Це можна зробити, і коли треба намалювати коло разом з його діаметром: вийшовши з одного кінця діаметра, пройти його, а потім по колу повернутися. Але як провести другий діаметр? Як би ми не намагалися, намалювати таку фігуру одним розчерком олівця не вдасться.
Легко намалювати коло, не відриваючи олівець від паперу й не проводячи двічі ніяку лінію. Це можна зробити, і коли треба намалювати коло разом з його діаметром: вийшовши з одного кінця діаметра, пройти його, а потім по колу повернутися. Але як провести другий діаметр? Як би ми не намагалися, намалювати таку фігуру одним розчерком олівця не вдасться.
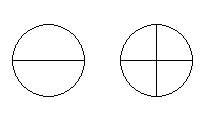
Напевно, коли-небудь хтось намагався намалювати будиночок, не відриваючи олівець від паперу й не проводячи їм двічі уздовж однієї лінії? Не відразу й не у всіх це виходило. А чому?
 У пункті 1 ми теж пробували намалювати фігури.
У пункті 1 ми теж пробували намалювати фігури.
Питання: « Чи можна кожну із цих фігур намалювати, не відриваючи олівець
від аркуша паперу, тобто одним розчерком?». Відповісти на нього нам з вами поки важко. Але цікаво, що подібним малюнком, за легендою є підпис пророка
Мухаммеда, який був безграмотний.
Більше 200 років тому схожою проблемою зацікавився знаменитий математик Леонард Ейлер. У той час жителі міста Кенігсберга ( тепер це місто називається Калінінград) полюбляли казати, що не хто не зможе оглянути центр їхнього міста, розташованого на берегах і двох островах ріки Преголота, пройшовши при цьому по кожному із семи мостів лише по одному разу й потім повернутися в початкову точку свого шляху. Ця задача так і називається:
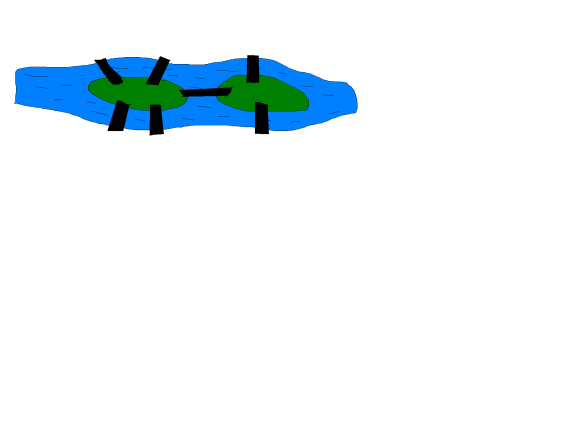 Задача про мости Кенігсберга
Задача про мости Кенігсберга
С c d g
р.Преголота A e D Треба обійти всі мости
У a b f міста так, щоб побувати на
кожному мосту тільки один раз.
Довгий час нікому не вдавалося впоратися із цією задачею. Головою міста була навіть заснована премія для того, хто розв'яже цю задачу. Багато хто намагався знайти відповідь, при цьому все йшли на мости й ходили по них. Л.Ейлер підійшов по-іншому до цієї зачачі: він намалював схематичну карту міста й позначив його чотири частини, відділені друг від друга водою буквами А, В, С, Д. Потім він позначив олівцем усеякі способи переходу по мостах з однієї частини міста в інші. Витративши на рішення не один день, Ейлер
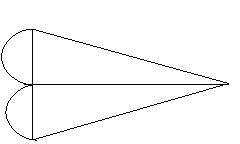 виніс вирок: «Обійти мости міста
виніс вирок: «Обійти мости міста
З Кенігсберга так, як цього хоче голова
А Д не можливо». Таким чином, задача про
мостах виявилася рівносильній задачі про
У малюванні одним розчерком. А розв'язок
задачі про мости доводить, що таку фігуру не можна намалювати одним розчерком. Із цього моменту починає розвиватися новий напрямок у геометрії - топологія, а саме в ній «теорія графів».
Її значення величезне, тому що завдяки топології можна вирішувати самі різні проблеми. Де в сучасному світі можна зустрітися з подібними задачами? (як відомо, ці мости давно зруйновані). Одна з важливих областей застосування її - проектування автострад і їхніх перехресть, розрахунок авіаційних маршрутів.
Зараз схеми, подібні до схеми, намальованої Л.Ейлером, зустрічається практично в будь-якій галузі: інженер креслить схеми електричних ланцюгів, хімік малює структурні формули, показуючи як у складній молекулі з'єднуються один з одним атоми, історик становить родовід, будуючи родовідне дерево, соціолог на діаграмі показує, як підкоряються один одному різні відділи однієї величезної корпорації.
В 30-ті роки ХХ століття німецький математик Дене Кенінг уперше провів систематичне дослідження подібних схем і дав їм загальну назву «ГРАФИ» ( походить від латинського слова «графіо» - пишу). Отже, що ж таке граф?
Граф - це фігура, що складається із точок, з'єднаних між собою відрізками, кривими лініями або дугами.
Точки називаються вершинами графа, а лінії, що з'єднують вершини – ребрами.
![]() ГРАФ
ГРАФ
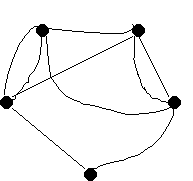

![]() суміжні вершини
суміжні вершини
![]() инцидентное ребро
инцидентное ребро

![]() петля
петля
Якщо ребро з'єднує дві вершини, то кажуть, що воно їм инцидентно.
Вершини, з'єднані ребром, називаються суміжними.
Дві вершини, що з'єднуються ребром, можуть збігатися; таке ребро називається петлею.
Вершина, з якої виходить тільки одне ребро, називається висяча вершина.

![]() висяча вершина
висяча вершина

![]()
![]()
![]()
![]() Вершина, що не належить ребрам, називається ізольована вершина.
Вершина, що не належить ребрам, називається ізольована вершина.
![]()
![]()
Граф, що складається з ізольованих вершин, називається нуль-граф.
![]()
![]()
![]()
![]()
![]()
![]() нуль-граф
нуль-граф



![]()
![]()
 Граф, у якому кожна пара вершин з'єднана ребром, називається повним графом.
Граф, у якому кожна пара вершин з'єднана ребром, називається повним графом.
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()

3.Степень вершини. Теорема парності.
Вивчаючи, задачу про мости, Л.Ейлер виявив, що для того щоб визначити можна намалювати граф, не проводячи по тому самому ребру двічі,(згадай наше питання) зовсім не обов'язково його намагатися накреслити. Досить порахувати, скільки ребер виходить із кожної його вершини.
Циклом (або ейлеровим шляхом) називається шлях, що з'єднує по одному разу всі ребра.
Граф, що володіє циклом, називають ейлеровим.
Якщо з вершини виходить непарне число ребер, то неї називають непарною, якщо ж виходить парне число ребер, те – парної.
 Кількість ребер, що виходять із однієї вершини, називають степенем вершини.
Кількість ребер, що виходять із однієї вершини, називають степенем вершини.
парна
непарна
Виявляється:1. Граф можна намалювати, не відриваючи олівець від паперу й проводячи по кожному ребру тільки один раз, якщо всієї його вершини парні, при цьому починати можна в будь-якій вершині й закінчити теж у кожній.
2.Граф тільки із двома непарними вершинами можна накреслити тільки одним розчерком, при цьому починати треба в одній непарній вершині, а закінчувати - в іншій непарній вершині.
Ці два твердження називаються теоремами Ейлера, графи, які їм підкоряються, називаються ейлеровими або унікурсальними (однопутними).
Глянь на таблицю й побудуй себе в зошиті таку ж. Підрахуй і простав у відповідних клітинках число парних і непарних вершин у кожного із цих графів. І заповни останній стовпчик, зрівнявши результат з теоремами Ейлера.
|
граф |
кількість вершин |
число парних вершин |
число непарних вершин |
Ейлеров (унікурсален) граф так чи ні |
|
1. |
|
|
|
|
|
2. |
|
|
|
|
|
3. |
|
|
|
|
|
4. |
|
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
|
![]()

![]()



![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
1. 2. 3.
![]()





![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 4. 5.
4. 5.

![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
6.
У кожного графа є вершини тої або іншої парності, але всі вони підкоряються
Теоремі парності.
Число непарних вершин будь-якого графа парно.
Задача.
У місті Маленькому 15 телефонів. Чи можна їх з'єднати проводами так, щоб кожний телефон був з'єднаний рівно з п'ятьома іншими?
Розв'язання:
Припустимо, що можливо. Тоді можна розглянути граф, вершини якого відповідають нашим телефонам, а ребра - це дроти, які їх з'єднують. Одержимо, що в нашім графі 15 вершин, степеня яких дорівнюють п'яти. Але за теоремою парності у кожного графа парне число вершин з непарним степенем, а число 15 непарне. Тому такого графа не існує. Виходить, з'єднати телефони так, як просять за умовою задачі неможливо.
Цю же задачу можна вирішити інакше, якщо задатися питанням: « А скільки тоді ребер буде мати такий граф?». Щоб підрахувати кількість ребер складемо степені всіх його вершин. Ясно, що при цьому кожне ребро буде підраховано двічі ( воно адже з'єднує дві вершини). Тому число ребер графа буде у два рази менше такої суми. У нашім випадку: 15![]() =37
=37![]()
Але адже це число неціле! Отже, такого графа не існує, тобто з'єднати телефони неможливо.
Висновок: кількість ребер будь-якого графа можна знайти, склавши степеня вершин, і отриманий результат розділити на два.
А тепер спробуй самостійно розв'язати задачі.
№1.
У державі 100 міст, з кожного виходить по 4 дороги. Скільки всього доріг у цій державі?
№2.
У класі 30 чоловік. Чи може бути так, що 9 з них мають по 3 друга, одинадцять- по 4 друга, а 10 - по 5 друзів?
№3.
Чи може в державі бути рівно 100 доріг, якщо з кожного міста веде 3 дороги; 6 доріг; 25 доріг?
№4.
У місті Маленькому 15 телефонів. Чи може бути так, що з них 4 телефони з'єднані кожний із трьома іншими, 8 телефонів з'єднані кожний із шістьома, 3 телефони - кожний з 12 іншими?
 Одні задачі. А як хочеться на уроках математики
Одні задачі. А як хочеться на уроках математики
пограти, помалювати, помандрувати. Як отут не
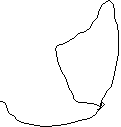
згадати відомого математика ХІХ століття Гамільтона, що придумав гру «Кругосвітня подорож». Він намалював карту, показану на малюнку, і запропонував прокласти по ній замкнутий маршрут, що проходить через всі точки, причому в кожній точці можна побувати лише один раз ( біля точок були написані назви міст, тому гру так назвали, а, до речі, що це нагадує?). Спробуй сам прокласти такий маршрут.
![]()
![]()
![]()
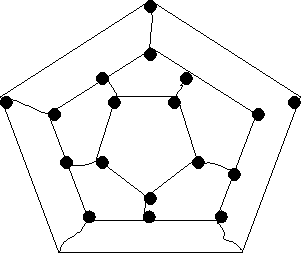
На честь Гамільтона, шляхи з такими властивостями на будь-якій карті, де зазначені точки й з'єднуючі їх лінії, називають гамільтоновими, а карти, на яких є такі шляхи - гамильтоновими графами.
У відмінності від ейлеровых шляхів, про гамильтонови шляхи відомо досить мало. Один з відомих фактів формулюється так:
якщо на карті досить багато відрізків, то гамільтонов шлях існує.
У всякому разі, необхідний шлях завжди існує, якщо не карті будь-які дві відзначені точки з'єднані лінією.
Цікаво, чи існує гамільтонов шлях на цьому малюнку?
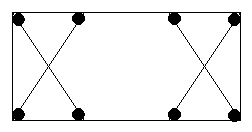
Задача про гамільтонови шляхи зустрічається в різних галузях. Наприклад, слюсар-ремонтник хоче оглянути всі верстати в цеху, побувавши в кожного верстата тільки один раз. Його шлях по цеху буде гамільтоновим. Зрозуміло, при цьому він хотів би, щоб шлях був найкоротшим. Багато років б'ються математики, намагаючись знайти загальний метод відшукання самого короткого шляху, однак дотепер ця задача не вирішена. Є тільки деякі правила, що дозволяють скоротити шлях. Може тобі вдасться розв’язати цю задачу в загальному випадку, коли виростиш?
 4. Зв'язний граф. Цикл. Граф-дерево.
4. Зв'язний граф. Цикл. Граф-дерево.
![]()
![]()
![]()
 Розглянемо кілька малюнків.
Розглянемо кілька малюнків.


![]()
![]()
![]()
![]()
![]()
![]()
![]() 1.2. 3.
1.2. 3.
Граф називається зв'язаним, якщо будь-які дві його вершини з'єднані послідовністю ребер, так, що кожне наступне починається наприкінці попереднього.
По кожному графу можна „гуляти”. Але не завжди можна повернутися туди, звідки почали свій шлях. Ви, напевно, пам’ятаєте як Том Сойер і Беки Тетчер блукали по ходах величезної печери й лише через кілька днів знайшли вихід з неї. Колись такі печери були притулком первісних людей, які відвойовували право жити в них у левів і ведмедів. Чи то на згадку про ці часи, чи те з інших причин, але люди стали зводити спорудження, вийти з яких було нелегше, ніж з такої печери. Грецький історик Геродот описує таке спорудження в Древньому Єгипті, причому за його словами, воно було більше вражаючим, чим навіть піраміди. Він називає його Лабіринтом і затверджує, що в ньому було 3 тисячі кімнат. Але самим знаменитим лабіринтом був все-таки не єгипетський, а той, що перебував на острові Кріт, лабіринт Міноса (згадай міф про нитку Аріадни).
Для математика, як і для будь-якої людини, цікаві ці сказання про давно минулі часи. Але його цікавить і чисто математичне питання: «А чи обов'язково потрібна була Тесею нитка Аріадни?». Чи не існує способу вибратися з лабіринту, не маючи такої нитки? Щоб не заблукати в лабіринті, треба, увійшовши в нього, доторкнутися рукою до стіни й далі йти, не відриваючи руки від стіни. Через деякий час ми знову будемо у входа в лабіринт.
Такий шлях називають замкнутим.
![]()
![]()
Замкнутий шлях (цикл)- шлях, початок і кінець, якого збігаються.
Як не згадати тут висловлення К. Пруткова:
«Де початок того кінця, яким закінчується початок».
Не завжди можна пройти по кожному ребру тільки один раз (а, до речі, коли це можна зробити?), але якщо це можливо, то такий шлях називають простим.
Простий шлях – шлях, у якому ніяке ребро не зустрічається двічі.

Задача.
Здороваються 4 чоловік. Скільки рукостискань буде в цій ситуації?
Звичайно, це можна легко підрахувати на практиці, ну, а якщо в залі присутній 30 чоловік. Адже не в кожному класі є 30 учнів, і перевірити це вже важко. А, якщо вирішили привітатися 500 чоловік, як бути? Для розв'язання цієї задачі ми маємо побудувати граф.
 І І етап- постановка задачі;
І І етап- постановка задачі;
ІІ 1 2 3 4 ІІ етап - за умовою є 4 чоловіки;
ІІІ етап - 1-ий здоровається з 2-им,
3-їм і 4-им; 2-ой здоровається з 3-їм
2 3 4 3 4 4 4-им; 3-ій здоровається тільки з 4-им,
з усіма іншими він уже привітався.
Таким чином, у нас відбувається 6 рукостискань. Для розв'язання цієї та багатьох інших аналогічних задач ми будуємо зв'язані графи, у яких немає циклів. Давайте перевернемо наш малюнок догори ногами й домалюємо ще одне ребро. Вийшло дуже схоже на дерево, як ми його малювали, коли були маленькими.
Такі графи так і називають - дерева.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()


 Дерево – зв'язаний граф, у якого
Дерево – зв'язаний граф, у якого
немає циклів.
Позначимо число вершин дерева буквою V, число ребер – буквою E. Тоді одержимо ще одну теорему:
У дереві число вершин на одиницю більше числа ребер. V-E=1
 Давайте розглянемо таке дерево. У кожного з нас є «Я», в
Давайте розглянемо таке дерево. У кожного з нас є «Я», в
кожного «Я» є мама й тато, у кожного з них теж є мама й
тато й у кожного з них теж є мама й тато й т.д.
Як же називається таке дерево? Генеалогічне - наше дерево життя, яким кожен повинен і може пишатися. Ти тільки подумай, адже тебе могло й не бути! Тільки уяви собі: скільки твоїх древніх предків повинні були чудом увернутися від бивня мамонта або стріли ворогів. Скільки твоїх пра-пра-прабабусь повинні були народити й виростити своїх синів і дочок, оберігаючи їх від нещасного випадку! Скільки стріл і куль повинні були минути твоїх пра-пра-прадідів. Як дивно, що саме твої предки вижили у всіх заледеніннях, потопах, війнах, епідеміях, революціях, пожежах! І в результаті цього грандіозного випадкового збігу всіх обставин з'являєшся ТИ! Представляєш, наскільки унікальна твоя персона!
Побудуй своє генеалогічне дерево й довідайся краще свої коріння.
 5. Плоский граф.
5. Плоский граф.
Задача.
У країні 30 міст, кожне з яких з'єднано дорогами з іншими. Скільки доріг можна закрити так, щоб з кожного міста можна було потрапити в будь-яке інше?
Розв'язання: усього в країні (30.29):2=435 доріг (кількість ребер графа). Простий шлях становить 30-1=29 доріг. Значить можна закрити 435-29=406 доріг.
На малюнку представлені декілька графів.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()





![]()
![]()
![]()
![]()
![]()



![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
Їх можна розбитий на дві групи:
1 група - графи, ребра яких перетинаються тільки у вершинах;
2 група - графи, ребра яких перетинаються в точках, які не позначені як вершини.
Графи, які належать першій групі, називають плоскими.
Граф, який можна намалювати так, щоб його ребра не перетиналися ніде крім вершин, називають плоским графом.
Дерево - це плоский граф.
Плоский граф ділить площину, на якій він намальований, на частини.
Позначимо: F - кількість частин площини;
V - кількість вершин графа;
E - кількість його ребер.
Тоді виконується наступна теорема:
Якщо плоский граф намальований правильно, то виконується умова:
V-E+F=2.
Задача.
У країні 7 озер, з'єднаних між собою 10 каналами так, що з будь-якого озера можна доплисти в кожне інше. Скільки в країні островів?
Розв'язання: у нашій задачі мова йде про плоский граф, значить він повинен підкорятися теоремі.
Озера - це вершини, V=4.
Канали - це ребра, Е=10.
Острови - це частини площини, F=х.
Одержуємо рівняння: 7-10+х=2; розв'язуючи його, знаходимо, що х=5, але островів 4, тому що навколо - материк.
Щоб завжди пам'ятати про те, що одна частина площини - це «материк», умовилися малювати плоскі графи у квадраті. Ось так:

![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1 2 1 2
1 2 1 2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 3 4 5 3 4 5
3 4 5 3 4 5
![]()
![]()
![]() Задача.
Задача.
 У лісі 4 хутори, з'єднаних між собою дорогами так, що ліс розбитий на 4 лісництва. Скільки доріг у лісі?
У лісі 4 хутори, з'єднаних між собою дорогами так, що ліс розбитий на 4 лісництва. Скільки доріг у лісі?
![]()
 Рішення: хутора – вершини - V=4
Рішення: хутора – вершини - V=4
![]() дороги – це ребра, Е=х, 22
дороги – це ребра, Е=х, 22
![]() лісництва - частини площини, F=4 3 1 2 3
лісництва - частини площини, F=4 3 1 2 3
Одержуємо рівняння: 4-х+4=2; Х=6 4
![]() Відповідь: у лісі 6 доріг. 4
Відповідь: у лісі 6 доріг. 4
 6. Ізоморфізм. Ліс.
6. Ізоморфізм. Ліс.
![]() Як ми вже відзначали, один й той самий граф можна намалювати різними способами. Так, однієї й тій же схемі вітань або однієї й тій же системі авіаліній можуть відповідати зовні не схожа одна на одну картинки.
Як ми вже відзначали, один й той самий граф можна намалювати різними способами. Так, однієї й тій же схемі вітань або однієї й тій же системі авіаліній можуть відповідати зовні не схожа одна на одну картинки.
Розглянемо наступний приклад: на турнірі п'яти команд А, В, С, Р, і Х команда зіграла з В, Р, і Х, крім того, С зіграла з Х и Р, а Р зіграла із С. Обидві картинки, зображені на малюнку, правильно відображають ситуацію.

![]() А
А

![]() Х Р А Р
Х Р А Р
![]() В
В
У С Х С
Два таких графи називають ізоморфними.
Два графи називаються ізоморфними, якщо в них однакова кількість вершин ( по n), і вершини кожного графа можна занумерувати числами від 1 до n так, щоб вершини першого графа були з'єднані ребрами тоді й тільки тоді, коли з'єднані ребрами відповідні ( занумерованими тими ж числами) вершини другого графа.
Задача.
Чи ізоморфні графи, зображені на малюнку?
1.



![]()
![]()


![]()
![]()

![]()
![]()
![]()
![]()


2.


![]()
![]()
 3.
3.
Залишилося з'ясувати, що ж таке ліс.
Виявляється, якщо в дереві можна виділити кілька маленьких «деревців», то такий граф-дерево називають ліс.
 Ліс – це граф-дерево, у якому можна виділити декілька граф-дерев.
Ліс – це граф-дерево, у якому можна виділити декілька граф-дерев.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()

![]()

![]()


![]()
![]()
 7.Задачі.
7.Задачі.
№1.
Між 9 планетами Сонячної системи введено космічне сполучення. Ракети літають по наступних маршрутах: Земля - Меркурій, Плутон - Венера, Земля - Плутон, Плутон - Меркурій, Меркурій - Венера, Уран - Нептун, Нептун - Сатурн, Сатурн - Юпітер, Юпітер - Марс, Марс - Уран. Чи можна добратися із Землі до Марса?
№2.
Чи може в державі, у якій з кожного міста виходить 3 дороги, бути рівно 100 доріг?
№3.
Чи можна намалювати на площині 9 відрізків так, щоб кожний перетинався рівно із трьома іншими?
№4.
Є група островів, з'єднаних між собою мостами так, що від кожного острова можна добратися до будь-якого іншого. Турист обійшов всі острови, пройшовши по кожному мосту рівно один раз. На острові Троєкратному він побував тричі. Скільки мостів веде з острова Троєкратного, якщо турист:
а) не з його почав і не на ньому закінчив;
б) з його почав, але не на ньому закінчив;
в) з його почав і на ньому закінчив?
№5.
Чи можна намалювати граф, зображений на малюнку, не відриваючи олівець від паперу й проводячи по кожному ребру рівно один раз?



№6.
У країні 50 міст, причому кожне з'єднане з кожним іншим. Яке найбільше число доріг можна закрити на ремонт так, щоб з кожного міста можна було потрапити до кожного?
№7.
Чи вірно, що дві графи ізоморфні, якщо:
у них по 10 вершин, ступінь кожної з яких дорівнює 9;
у них по 8 вершин, ступінь кожної з яких дорівнює 3;
вони зв'язні, без циклів і в них по 6 ребер?
 Розділ 3. Алгебра логіки.
Розділ 3. Алгебра логіки.
3.1. Поняття про логіку. Висловлення. Нуль і одиниця.
«Я мислю - виходить, я існую», сказала одна дуже відома
людина. Уміння думати відрізняє людину від інших істот, які живуть на нашій планеті. Напевно за такий довгий час, що людина розумна живе на Землі, повинні були виникнути закони, яким підкоряється його вміння мислити. І така наука теж повинна була з'явитися, яка навчить нас мислити правильно, здраво, логічно. І вона з'явилася – це Логіка.
Слово «логіка» походить від грецького слова «логос», що з одного боку, означає «слово» або «мова», а з іншого боку - те, що виражається в мові, тобто мислення.
Логіка вивчає ті аспекти мислення, які фіксовані в мові у вигляді слів, речень і їх сукупностей. Тому логіка має безпосереднє відношення до мови.
Логіка як наука сформувалася дуже давно, ще в IV столітті до н.е. ЇЇ створив давньогрецький філософ Аристотель. У плині багатьох століть логіка майже не розвивалася. Це, звичайно, свідчить про геніальність Аристотеля, якому вдалося створити настільки повну наукову систему. Однак у силу такої незмінності логіка придбала славу мертвої, застиглої науки й викликала до себе в багатьох скептичне відношення. Так тривало аж до середини XIX століття, коли ірландським математиком Джорджем Булем була створена алгебра логіки, у якій діяли закони, схожі на закони звичайної алгебри, але літерами позначаються не числа, а твердження. Вона так і стала називатися «булева алгебра». Мовою цієї булевой алгебри можна описувати міркування й «обчислювати» їхні результати.
 Алгебра логіки Буля стала основою для появи нової науки - математичної логіки. Сама назва каже багато про що. Математична логіка була викликана до життя потребами математики, і використовує вона мову й методи математики.
Алгебра логіки Буля стала основою для появи нової науки - математичної логіки. Сама назва каже багато про що. Математична логіка була викликана до життя потребами математики, і використовує вона мову й методи математики.
Сьогодні математична логіка використовується в біології, медицині,
лінгвістиці, психології, економіці, техніці. Величезна її роль
у розвитку обчислювальної техніки: вона використовується
в конструювання ЕОМ і при розробці штучних мов для спілкування з маши-
нами.
Наша мова, тексти, які ми читаємо й пишемо, складаються із речень. Це стосується й звичайної мови, і математичної мови. Те, про що говориться в кожному твердженні, може виявитися вірним або невірним. Наприклад, у підручнику можна прочитати вірне твердження «Земля обертається навколо Сонця», а якщо учень напише, що Сонце супутник Землі, то це вже буде невірне твердження. Хоча в підручниках теж зустрічаються хибні твердження - через помилки або через неуважність.
Часто замість слів «вірно» або «невірно», кажуть істинно або хибне.
Отож усяке твердження, відносно якого має сенс казати, що воно істинно або хибне, називається висловленням.
У будь-якому висловленні можна виділити те, про що говориться, і те, що про це повідомляється. Наприклад, у твердженні «Земля обертається навколо Сонця», говориться про планету Земля й повідомляється, що вона обертається навколо Сонця. Так само й у математичному твердженні 30+20=50, говориться про суму чисел 30 і 20 і повідомляється, що вона дорівнює 50.
Усяке висловлення або істинно, або хибне. Ні про що не можна сказати так, щоб це твердження було й істинним і хибним одночасно. Але не про всяке висловлення можна відразу сказати яке воно - істинно або хибне. Так сталося із твердженням:
5
«Число 1+22 =429496297 – просте».
Це висловлення належить великому французькому математикові П'еру
Ферма ( 1601 - 1665). Ясно, що це число одночасно бути простим і складним не може. Тому це твердження або істинно, або хибне, тобто воно є висловленням. Але тільки в 1732 році Ейлеру вдалося довести, що воно помилково.
Звичайно, коли мова йде про більш прості або відомі речі ми відразу можна відзначити істинно воно або хибне. Кожному елементарному висловленню вже приписане або значення істини, або значення, що воно хибне.
У першому випадку кажуть, що елементарному висловленню поставлено у відповідність число 1, у другому - число 0.
Алгебра логіки не вступає в суперечку про те, істинно висловлення або хибне. Алгебра логіки не займається обґрунтуванням того, чому тому або іншому висловленню приписують значення, що воно істинно або хибне. Ці питання вирішуються поза цією наукою. До речі кажучи, алгебру логіки не цікавить і значеннєвий зміст висловлення. Вона цікавиться тільки однією властивістю висловлень: бути істинним або хибним. Таке звуження інтересів дає можливість вивчати висловлення алгебраїчними методами, дозволяє ввести деякі операції над елементарними висловленнями й з їхньою допомогою будувати й вивчати як завгодно складні висловлення.
 Не всяке твердження є висловленням. Якщо хто-небудь запитує «Котра годину?» або кричить «Привіт», не має ніякого сенсу говорити про те, істинні чи ні ці речення. Не є висловленнями й такі твердження: «Каша – смачне блюдо», «Математика – легкий предмет», тому що немає єдиної думки про те, істинні ці твердження або хибні, комусь подобається їсти кашу, а комусь подобається розв'язувати задачі. Твердження: «Ішов дощ», «Площа кімнати
Не всяке твердження є висловленням. Якщо хто-небудь запитує «Котра годину?» або кричить «Привіт», не має ніякого сенсу говорити про те, істинні чи ні ці речення. Не є висловленнями й такі твердження: «Каша – смачне блюдо», «Математика – легкий предмет», тому що немає єдиної думки про те, істинні ці твердження або хибні, комусь подобається їсти кашу, а комусь подобається розв'язувати задачі. Твердження: «Ішов дощ», «Площа кімнати
20м2»,- вимагають додаткових відомостей (коли й де йшов дощ, про яку саме кімнату мова йде), а значить про їхню істинність або хибність теж нічого не можна сказати.
Але вистачить теорії, настав час переходити до практики.
Спробуй виконати наступні завдання.
Завдання №1.
Серед даних тверджень знайдіть висловлення й укажіть те, про що говориться й те, що про це повідомляється.
- Коли закінчуються літні канікули?
- Навчальний рік на Україні починається 1 вересня.
- Яка краса!
- Число 3 є дільником числа 18.
- Київ - столиця України.
- Сума п'яти й тринадцяти.
- Мені подобається ця картина.
- Сьогодні гарна погода.
Завдання №2.
У даних висловленнях укажіть те, про що говориться, і те, що про це повідомляється. Які із цих висловлень щирі, а які - хибні?
- У кожному лютому 28 днів.
- У кожному серпні 31 день.
- Наступний день після понеділка - п'ятниця.
- У слові «математика» 5 складів.
- Слово «математика» можна перенести з одного рядка на іншу п'ятьома способами.
- Слова «гуляти» дієслово.
- Сума всіх десяти цифр дорівнює 45.
- Усяке тризначне число більше 100.
-


 Існує найбільше число.
Існує найбільше число.
- Існує найбільше п'ятизначне число.
-


 Існує найменше натуральне число.
Існує найменше натуральне число.
-


 На малюнку зафарбовано
На малюнку зафарбовано 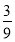 квадрата.
квадрата.
Завдання №3.
Придумайте одне істинне й одне хибне висловлення. Наведіть приклади твердженнь, які не є висловленнями.
Завдання №4.
Визначите істинність висловлень і запишіть істинні за допомогою знаків < , >,=
- три менше п'яти; 2) п'ять більше трьох;
3) п'ять менше трьох; 4) три дорівнює трьом.
Завдання №5.
Які з висловлень істинні, а які хибні?
- 3>1;
- 9<12;
- 12 - найменше натуральне число, що ділиться на 6;
- 5 - просте число;
- 4 - парне число;
- Рим -столиця Німеччини;
- У Сонячній системі 9 великих планет;

3.2 Заперечення.
Під час суперечки, одні зі сперечальників вважають деякі твердження істинними, а інші - ці ж твердження - хибними. Так, у плині багатьох століть учені сперечалися про те, істинно або хибне твердження «Сонце обертається навколо Землі». Всі тоді були впевнені, що це твердження істинно, і не просто істинно, а очевидно, лише деякі намагалися затверджувати зворотне.
 Італійського ченця Джордано Бруно, що казав, що це не так, спалили за це на багатті. Пройшло багато часу до того, як довели, що це не так.
Італійського ченця Джордано Бруно, що казав, що це не так, спалили за це на багатті. Пройшло багато часу до того, як довели, що це не так.
При суперечці двох людей одна людина затверджує, що деяке
висловлення істинно, а інша заперечує цю думку, вона має
протилежну.
Наприклад, якщо учень, обчислює значення виразу 127+552, і написав у відповіді число 678, а вчитель перекреслив цю відповідь, то в них протилежні думки із приводу суми цих чисел. Можна сказати, що твердження
127+552=678 і 127+552![]() 678
678
заперечують один одного. Кожне з них називають запереченням іншого.
Розглянемо ще кілька прикладів таких висловлень, записавши їх у таблицю.
|
№ |
Висловлення |
Заперечення |
|
1 |
Київ – столиця України. |
Київ не є столицею України. |
|
2 |
Двічі два – п'ять. |
Двічі два не дорівнює п'яти. |
|
3 |
Існує найменше натуральне число. |
Не існує найменшого Натурального числа. |
|
4 |
Існує найбільше натуральне число. |
Не існує найбільшого натурального числа. |
|
5 |
2 більше, ніж 2. |
2 не більше, ніж 2. |
|
6 |
30 ділиться на 7. |
30 не ділиться на 7. |
|
7 |
У Сашка є старший брат. |
У Сашка немає старшого брата. |
І в житті, і в математиці дуже часто доводиться зустрічати заперечення, тому дуже важливо навчитися правильно формулювати ці самі заперечення. Для цього буває недостатньо на початку даного висловлення приписати слова «Невірно, що», або слово «ні» десь у його середині. Наприклад, заперечення до висловленні №7 тоді б звучало так: «Невірно, що в Сашка є брат». Але адже кожний з нас скаже просто: «У Сашка немає старшого брата». Так, що, здається, прийдеться попрацювати над цим. Хоча, ті хто вивчає іноземну мову, уже неабияк у цьому напрактикувалися: запис даної пропозиції « у негативній формі» - це і є формулювання заперечення.
Логічна операція, що відповідає логічному зв'язуванню «ні», «невірно, що» називається запереченням.
Якщо дане твердження істинно, то його заперечення хибне, і навпаки, якщо дане твердження хибне, те його заперечення істинно.
Тобто одне із двох твердженнь обов'язково істинно – або дане твердження, або його заперечення. Це закон виключення третього.
Для позначення заперечення використовується рисочка над висловленням ![]() або схожий на «мінус» знак
або схожий на «мінус» знак ![]() А. Для висловлень можна скласти так звану таблицю істинності.
А. Для висловлень можна скласти так звану таблицю істинності.
|
А |
|
|
1 |
0 |
|
0 |
1 |
 Формулювати заперечення нелегко, тому прийшов час попрацювати над цим.
Формулювати заперечення нелегко, тому прийшов час попрацювати над цим.
Завдання №1.
 Побудуйте заперечення висловлень за допомогою слів «невірно, що», а потім перефразуйте їх у більш прості форми.
Побудуйте заперечення висловлень за допомогою слів «невірно, що», а потім перефразуйте їх у більш прості форми.
- Місяць - супутник Землі.
- Мухомор - їстівний гриб.
- У Дніпру водяться алігатори.
- На Землі 7 материків.
- На Марсі немає життя.
Завдання №2.
Побудуйте заперечення висловлень, укажіть істинність висловлень і їхніх заперечень.
- А={Всі ріки впадають у Чорне море}.
- В={Кавун - це фрукт}.
- С={Сонце - супутник Венери}.
Завдання №3.
Запишіть твердження математичною мовою й побудуйте до них заперечення:1) число х менше п'яти;
- число в більше або дорівнює 10;
- різниця чисел а й с дорівнює числу d;
- сума чисел а й b дорівнює числу с.
 3.3.Правила утворення заперечень висловлювань.
3.3.Правила утворення заперечень висловлювань.
Деяким з вас уже доводилося зустрічатися з задачами, у яких треба відповістити на питання, роблячи деякі логічні висновки. Це спершу зовсім непросто. Однієї з головних причин логічних помилок, що виникають у процесі розв'язання таких задач і вивчення шкільних дисциплін, особливо математики, є невміння правильне будувати заперечення конкретних математичних тверджень, а саме тоді, коли ці твердження мають складну структуру.
 Якщо у висловленні мова йде про один якийсь предмет, Твій горіх?
Якщо у висловленні мова йде про один якийсь предмет, Твій горіх?
то для заперечення цього висловлення досить використовувати Не твій горіх!
частку «ні». Мій!!!
 Наприклад, для висловлення « 4 – парне число», висловлення
Наприклад, для висловлення « 4 – парне число», висловлення
«4 не є парним числом» є запереченням;
запереченням висловлення « число а ділиться на 6»
є висловлення «число а не ділиться на 6» .
Виходить, що якщо висловлення має структуру
« Х є А», то його запереченням є висловлення « Х не є А».
Здається все просто. Але не отут-то було!
Розглянемо висловлення такого виду «Всі натуральні числа діляться на 5». Використовуючи частку «ні», одержимо висловлення «Всі натуральні числа не діляться на 5». Однак це висловлення не можна вважати запереченням
даного, тому що, ми одержали, що обидва висловлення одночасно хибні, а таблиця істинності, побудована нами на підставі законів логіки, каже нам, що якщо А хибне, то ![]() повинне бути істинно. Тому в таких ситуаціях не можна формулювати заперечення, використовуючи таку структуру.
повинне бути істинно. Тому в таких ситуаціях не можна формулювати заперечення, використовуючи таку структуру.
Висловлення виду «Всі Х мають властивість А» відносяться до загальних висловлень. Запереченням висловлень такого виду є висловлення « Деякі Х не мають властивості А».
Тепер, якщо сформулювати заперечення нашому висловленню, ми одержимо твердження « Деякі натуральні числа не діляться на 5». І це висловлення буде істинно. Інакше це можна сформулювати так «Невірно, що всі натуральні числа діляться на 5» або навіть так «Існує таке натуральне число, що не ділиться на 5».
Щоб побудувати заперечення висловлення виду «Всі Х мають властивість А», достатнє слово «всі» (або його синонім) замінити словом «деякі» (або його синонімом) і утворити заперечення твердження, що стоїть за цим словом.
Давайте розглянемо зворотну ситуацію: дано висловлення виду «деякі Х мають властивість А» і треба побудувати його заперечення.
Наприклад, дано висловлення «Деякі натуральні числа - парні». Якщо ми спробуємо побудувати його заперечення, використовуючи частку «ні», то одержимо висловлення «Деякі натуральні числа - непарні». При цьому ми одержали два істинних висловлення, а такого, як відомо, бути не може. Тоді заперечення цього висловлення повинне починатися зі слів «Невірно, що...». Тому вірне заперечення висловлення даного виду має структуру «Невірно, що деякі Х мають властивість А». Виходить, заперечення нашого висловлення має вигляд «Невірно, що деякі натуральні числа - парні». Спробуємо сформулювати простіше. Міркуємо так: оскільки неправильно, що деякі Х мають властивість А, то правильним є висловлення «Не існує такого Х, що має властивість А» або «Всі Х не мають властивості А».
Одержали, що «деякі Х мають властивість А» і треба побудувати його заперечення.
Щоб побудувати заперечення висловлення «Деякі Х мають властивість А» достатнє слово «деякі» (або його синонім) замінити словом «всі» (або його синонімом) і утворити заперечення твердження, що стоїть за цим словом.
До речі кажучи, щоб побудувати заперечення до цих висловлень ми використовували закон виключення третього (до речі, як він формулюється?).
Перевіримо, як ви засвоїли ці правила?
 Завдання №1.
Завдання №1.
Побудуйте заперечення загальних висловлень. Переконаєтеся у виконання для них закону виключення третього.
- У будь-якому місті України є пам'ятники історії.
- Планети мають форму кулі.
- Всі європейські держави мають Конституцію.
- Вода є на будь-якій планеті.
- Питальне речення не може бути висловленням.
- Висловлення завжди оповідальне речення.
- У кожної планети Сонячної системи є природний супутник.
- Вода є на будь-якій планеті.
Завдання №2.
Визначите вид висловлення. Знайдіть істинні висловлення. Для хибних загальних висловлень побудуйте заперечення й наведіть контрприклад.
- Кожне натуральне число ділиться на 1 і на себе.
- Деякі числа мають тільки один дільник.
- Будь-яке натуральне число має хоча б два дільники.
- Просте число завжди менше складеного.
- Взаємно прості числа самі є простими.
- Дільник числа завжди менше самого числа.
- Кратне числа завжди більше самого числа.
- Числа 12 і 15 - взаємно прості.
Завдання №3.
Сформулюйте дані висловлення за допомогою слова «існує». Побудуйте їхнє заперечення й переконаєтеся у виконання для них закону виключення третього.
- Черепахи можуть жити до 300 років.
- Деякі тварини занесені в Червону книгу.
- Є ссавці, які живуть у воді.
- Речення може не мати підмета.
- Висловлення може бути питальним реченням.
- Є країни, які є острівними державами.
Завдання №4.
Визначите вид висловлення й побудуйте заперечення. Переконаєтеся у виконання для них закону виключення третього.
- Всі лікарі - стоматологи.
- Деякі музиканти - піаністи.
- Вода іноді буває твердої.
- В Арктиці ростуть пальми.
- Кожна людина вміє співати.
 3.4.Кон'юнкція.
3.4.Кон'юнкція.
« Жив собі на світі хлопчик Петро. Петро не любив історію. Петро любив математику. От такий був хлопчик Петя.»
Не дуже красиво написали про хлопчика, але в цьому реченні можна виділити кілька висловлень. Наприклад, висловлення А={Петро не любить історію} і В={Петро любить математику}. Ці два твердження можна об'єднати в одне: «Петро не любить історію й любить математику». Два висловлення А и В теж можна об'єднати в одне й допоможе в цьому нам конъюнкция.
Кон'юнкція - від латинського слова conjunctio - з'єднання, зв'язок.
Кон'юнкціею (або логічним добутком) висловлень А и В називається висловлення «А и В», що істинно тоді й тільки тоді, коли А істинно й В істинно.
Позначають кон'юнкцію так: А![]() В, А@В, А .В. Найчастіше використовують позначення А
В, А@В, А .В. Найчастіше використовують позначення А![]() В. Читають «А і В».
В. Читають «А і В».
Досить часто для вираження кон'юнкції замість сполучника «і» використовують сполучники «а», «але», «хоча», «однак», і ін.. Оскільки сполучник «і» не завжди позначає кон’юнктивний зв'язок твердженнь. Наприклад, розглянемо два висловлення: « 3 і 5 - прості числа» і « 3 і 5 взаємно прості числа». Перше висловлення - скорочений запис кон'юнкції «3 - просте число» і «5 - просте число». Друге висловлення - елементарне, котре виражає зв'язок між двома числами 3 і 5, який полягає в тому, що в них немає спільного дільника, відмінного від одиниці. Тому у другому висловленні сполучник «і» зв'язує не дві думки, а два предмети, між якими є певний зв'язок. Логічний сполучник „і” відрізняється від граматичного сполучника «і» ще й тим, що логічним сполучником можна з'єднувати будь-які думки. Наприклад, твердження «число 55 ділиться на 5 і Шумахер - автогонщик» в логіці є істинним, тому що єдиною умовою для того, щоб кон’юнктивне твердження було істинним, є істинність кожного з них. З погляду смислу, це судження не має взагалі ніякого сенсу.





Якщо ми заговорили про істинність, то настав час побудувати таблицю істинності. На відміну від заперечення, що залежить від одного елементарного висловлення, кон'юнкція залежить від двох елементарних висловлень.
|
№ |
А |
В |
А |
|
1. |
1 |
1 |
1 |
|
2. |
1 |
0 |
0 |
|
3. |
0 |
1 |
0 |
|
4. |
0 |
0 |
0 |
Повернемося до хлопчика Петра. Ми знаємо, що А={Петро не любить історію} і В={Петро любить математику}. Відповідно до визначення, кон'юнкція двох елементарних висловлень істинна тільки в тому випадку, коли істинні обидва висловлення, які її утворюють (рядок 1), і хибна в будь-якому іншому випадку (рядки 2,3,4). В нашому прикладі кон'юнкція
А![]() В={Петро не любить історію й любить математикові}
В={Петро не любить історію й любить математикові}
істинна тільки тоді, коли Петро не любить історію й любить математику. В інших випадках, тобто коли Петро:
- не любить історію й не любить математикові;
- любить історію й любить математикові;
- любить історію й не любить математикові
висловлення А![]() В хибне.
В хибне.
 А зараз займемося практикою.
А зараз займемося практикою.
Завдання №1.
Визначите значення істинності висловлень:
- Київ розташований на Дніпру й 4+5=9;
- Число 3 - парне й це число простої;
- 2.2=4 і 2<3;
- 25 ділиться на 6 і Дніпро впадає в Тихий океан.
Завдання №2.
Визначите істинність висловлення А, якщо:
-
«А
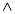 (5+5=10)»=1;
(5+5=10)»=1;
-
«А
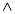 (5+5=10)=0.
(5+5=10)=0.
Завдання №3.
Складіть 3-4 складні висловлення на кон'юнкцію, визначить їх істинність.

3.5.Диз'юнкція.
Записуючи висловлення «число 55 ділиться на 5 і Шумахер – автогонщик», учень помилився й замість сполучника «і» написав «або». Вийшло начебто б те, та не зовсім: «число 55 ділиться на 5 або Шумахер – автогонщик». В логіці будь-яка зміна відіграє величезну роль, да і з граматичної точки зору сполучник «або» не з'єднує, а роз'єднує. Ось і вийшло: або 55 ділиться на 5, або Шумахер – автогонщик. А разом – ніяк. Це називається диз'юнкція.
Диз'юнкцією (лат.disjunctio – поділ) називається операція, що кожним двом елементарним висловленням А и В ставить у відповідність нове висловлення «А або В», що хибне тоді, коли хибні складні висловлення А и В. У всіх інших випадках висловлення «А або В» істинно.
Позначають диз'юнкцію так: А![]() В, А+В. Читають «А або В», «має місце А або В».
В, А+В. Читають «А або В», «має місце А або В».
В математиці сполучник «або» завжди розуміють у широкому змісті. Висловлення А![]() В (А або В) істинно, якщо: А істинно, а В хибне; А хибне, а В істинно; А істинно й В істинно.
В (А або В) істинно, якщо: А істинно, а В хибне; А хибне, а В істинно; А істинно й В істинно.
Тому таблиця істинності виглядає так:
|
№ |
А |
В |
А |
|
1. |
1 |
1 |
1 |
|
2. |
1 |
0 |
1 |
|
3. |
0 |
1 |
1 |
|
4. |
0 |
0 |
0 |





З кон'юнкцією ми попрактикувалися (до речі, що спільного мають і чим відрізняються кон'юнкція й диз'юнкція?). Попрактикуємося тепер з диз'юнкцією.
 Завдання №1.
Завдання №1.
Визначите значення істинності висловлень:
- Київ розташований на Дніпру або 4+5=9;
- Число 3 - парне або це число простої;
- 2.2=4 або 2<3;
- 25 ділиться на 6 або Дніпро впадає в Тихий океан.
Завдання №2.
Визначите істинність висловлення В, якщо:
-
«В
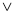 (5+5=0)»=1;
(5+5=0)»=1;
-
«В
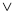 (5+5=0)»=0.
(5+5=0)»=0.
Завдання №3.
Складіть 3-4 складні висловлення на диз'юнкцію, визначить їх істинність.
 3.6. Імплікація.
3.6. Імплікація.
Дуже часто в розмові з кимось ми вживаємо висловлювання
«Якщо ..., то...». Наприклад, «Якщо на вулиці буде сніг, то ми
підемо кататися на санчатах», «Якщо я не вивчу урок, то можу одержати завтра двійку» і так далі.
Нехай у нас є два елементарних висловлення А и В. Складаючи з них висловлення, використовуючи конструкцію «Якщо..., то...», одержимо наступне висловлення «Якщо А , то В».
Імплікацією висловлень А и В називається висловлення «якщо А, то В», що хибне тільки тоді, коли, А істинно, а В хибне. В усіх інших випадках висловлення «якщо А, то В» істинно.
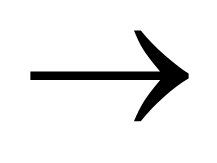
Позначають імплікацію висловлень А и В так: А![]() В, або А
В, або А![]() В, або А
В, або А![]() В.
В.
Читають: «якщо А, те В», «з випливає В».
Члени імплікації А![]() В називають так: А – попереднім членом, умовою або антецедентом імплікації; В – наступним членом, висновком або консекведентом імплікації.
В називають так: А – попереднім членом, умовою або антецедентом імплікації; В – наступним членом, висновком або консекведентом імплікації.
З огляду на визначення одержуємо таблицю істинності:
|
№ |
А |
В |
А |
|
1. |
1 |
1 |
1 |
|
2. |
1 |
0 |
0 |
|
3. |
0 |
1 |
1 |
|
4. |
0 |
0 |
1 |


 Розглянемо наступні висловлення:
Розглянемо наступні висловлення:
- Якщо 2+2=4, то Дніпро впадає в Чорне море;
- Якщо 2+2=4, то Дніпро впадає в Біле море;
- Якщо 2+2=5, то Дніпро впадає в Чорне море;
-
Якщо 2+2
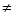 5, то Дніпро впадає в Біле море.
5, то Дніпро впадає в Біле море.
З визначення імплікації маємо, що хибним є тільки друге висловлення, всі інші істинні.

 Розглянемо наше висловлення «Якщо число 55 ділиться на 5, то Шумахер – автогонщик». Одержуємо, що воно істинне, хоча ніякого зв'язку між тим, що 55 ділиться на 5 і автоперегонами не спостерігається.
Розглянемо наше висловлення «Якщо число 55 ділиться на 5, то Шумахер – автогонщик». Одержуємо, що воно істинне, хоча ніякого зв'язку між тим, що 55 ділиться на 5 і автоперегонами не спостерігається.



З таблиці істинності випливає, що імплікація має властивості:
1)А![]() 1=1, 2)1
1=1, 2)1![]() А=А, 3)А
А=А, 3)А![]() 0=
0=![]() , 4)0
, 4)0![]() А=1.
А=1.
Рівносильність А![]() 1=1 означає, що істинне висловлення є висновком як істинної, так і хибної умови. Інакше, істина випливає як із істинного, так і з хибного висловлення. Тобто істина може випливати із чого завгодно. Аналогічно, рівносильність 0
1=1 означає, що істинне висловлення є висновком як істинної, так і хибної умови. Інакше, істина випливає як із істинного, так і з хибного висловлення. Тобто істина може випливати із чого завгодно. Аналогічно, рівносильність 0![]() А=1 означає, що з хибного висловлення ( з хибної умови) випливає все що завгодно, тобто як хибне, так і істинне висловлення.
А=1 означає, що з хибного висловлення ( з хибної умови) випливає все що завгодно, тобто як хибне, так і істинне висловлення.
Зазначені особливості, на них першим звернув увагу Аристотель, указавши, що з хибного випливає як істинне, так і хибне, називають парадоксами імплікації.
Дуже дивна операція, чи неправда? Але що поробиш, така вона логіка.
А в нас знову підійшов час практики.
 Завдання №1.
Завдання №1.
Визначите значення істинності висловлень:
- Якщо 12 ділиться на 6, то 12 ділиться на 3;
- Якщо Київ розташований на Місяці, то білі ведмеді ходять у школу;
- Якщо 15 ділиться на 3, то 15 ділиться на 6.
Завдання №2.
Визначите значення істинності висловлення А, якщо:
- {Якщо 4 - парне число, те А}=1;
- {Якщо А, те 4 - непарне число}=1;
- {Якщо 6 - парне число, те А}=0;
- {Якщо А, те 6 - парне число}=0.
Завдання №3.
Дано висловлення:
А={9 ділиться на 3} і В= {10 ділиться на 3}.
Визначите значення істинності висловлень:
1)А![]() В, 2) В
В, 2) В![]() А, 3)
А, 3) ![]()
![]() В, 4)
В, 4)![]()
![]() А,
А,
5) ![]()
![]()
![]() , 6)
, 6) ![]()
![]()
![]() , 7)А
, 7)А![]()
![]() , 8)В
, 8)В![]()
![]() .
.
Завдання №4.
Сформулюйте у вигляді імплікації наступні твердження:
- У всякий трикутник можна вписати окружність;
-
Сума кутів трикутника дорівнює 180
 .
.
 3.7.Эквіваленція двох висловлень.
3.7.Эквіваленція двох висловлень.
Ну чому «Якщо вивчиш уроки, то одержиш гарну
оцінку»? От би не вчити , а гарні оцінки одержувати. Але так не буває, тому що це висловлення можна із упевненістю замінити на інше: «Гарну оцінку одержиш тоді й тільки тоді, коли вивчиш уроки». Ось так! У логіці й для таких висловлень теж є своя назва й свої закони. Називають такі висловлення эквіваленція.
Якщо А и В два елементарних висловлення, то эквіваленціей висловлень А и В називається висловлення «А тоді й тільки тоді, коли В», що істинно тільки за умови, що висловлення А и В однакової істинності (тобто обидва істинні або обидва хибні).
Позначають эквіваленцію висловлень А и В так: А![]() В, або А
В, або А![]() В, або А
В, або А![]() В. Для утворення эквіваленції використовують висловлювання « у тому і тільки в тому випадку», «тоді й тільки тоді» і інші аналогічні їм.
В. Для утворення эквіваленції використовують висловлювання « у тому і тільки в тому випадку», «тоді й тільки тоді» і інші аналогічні їм.
За визначенням одержуємо таблицю істинності:
|
№ |
А |
В |
А |
|
1. |
1 |
1 |
1 |
|
2. |
1 |
0 |
0 |
|
3. |
0 |
1 |
0 |
|
4. |
0 |
0 |
1 |

З таблиці істинності випливає, що імплікація має властивості:
1)А![]() 1=1
1=1![]() А=А;
А=А;
2)А![]() 0=0
0=0![]() А=
А=![]() ;
;
Розглянемо два висловлення:
А={На дубі поспіють яблука} і В={Ваня Сидоров стане чемпіоном}.
Эквіваленціей цих висловлень є висловлення
А![]() В={На дубі поспіють яблука тоді й тільки тоді, коли Ваня Сидоров стане чемпіоном}.
В={На дубі поспіють яблука тоді й тільки тоді, коли Ваня Сидоров стане чемпіоном}.
Це висловлення істинно, якщо:
1) На дубі поспіють яблука й Ваня Сидоров стане чемпіоном;
2)На дубі не поспіють яблука й Ваня Сидоров не стане чемпіоном.
Хибне воно буде, якщо:
1)На дубі поспіють яблука, Ваня Сидоров не стане чемпіоном;
2)На дубі не поспіють яблука, а Ваня Сидоров стане чемпіоном.
Ми вже розібрали достатню кількість логічних операцій. Зв'язок эквіваленції з попередніми логічними операціями, наприклад, виглядає так:
А![]() В=(А
В=(А![]() В)
В)![]() (В
(В![]() А) тобто
А) тобто
висловлення «А виконується тоді й тільки тоді, коли В» рівносильно виконанню кон'юнкції двох висловлень: «Якщо А, те В» і «Якщо В, те А».
Щоб у цьому переконатися побудуємо таблицю істинності.
|
№ |
А |
В |
А |
(А |
|
1. |
1 |
1 |
1 |
1 1 1 |
|
2. |
1 |
0 |
0 |
0 0 1 |
|
3. |
0 |
1 |
0 |
1 0 0 |
|
4. |
0 |
0 |
1 |
1 1 1 |

![]()
![]()
![]()
 Ось така складна, але цікава ця наука логіка. Увесь час треба практикуватися.
Ось така складна, але цікава ця наука логіка. Увесь час треба практикуватися.
Завдання №1.
Визначить значення істинності висловлювань:
- 12 ділиться на 6 тоді й тільки тоді, коли 12 ділиться на 3;
- 13 ділиться на 6 тоді й тільки тоді, коли 13 ділиться на 3;
- 15 ділиться на 6 тоді й тільки тоді, коли 15 ділиться на 3;
- Сонце сходить на сході в тому і тільки в тому випадку, якщо воно заходить на заході.
Завдання №2.
Дано висловлення:
А={9 ділиться на 3} і В= {10 ділиться на 3}.
Визначите значення істинності висловлень:
1)А![]() В, 2)
В, 2)![]()
![]() В, 3)
В, 3)![]()
![]()
![]() , 4)А
, 4)А![]()
![]() .
.
Завдання №3.
Визначите значення істинності висловлення А, якщо:
-
{ А
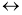 (7>4)}=1;
(7>4)}=1;
-
{ А
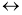 (7<4)}=1;
(7<4)}=1;
-
{ А
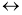 (7<4)}=0;
(7<4)}=0;
-
{ А
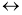 (7>4)}=0.
(7>4)}=0.
Завдання №4.
Дано два помилкових висловлення:
А={Число 3 є дільником числа 20} і В={Число 5 - парне число}. У чому полягають наступні висловлення:
1) ![]() ; 2) А
; 2) А![]() В ; 3) А
В ; 3) А![]() В; 4) А
В; 4) А![]() В; 5) А
В; 5) А![]() В.
В.
Які із цих висловлень істинні, а які - хибні?
 3.8. Тотожньо-істинні й
3.8. Тотожньо-істинні й
тотожньо-хибні висловлення.
Вивчені нами п'ять логічних операцій дають нам можливість, маючи
первісний набір елементарних висловлень, побудувати більше складні висловлення. Операції в таких логічних виразах виконуються з ліва на право із урахуванням дужок. Відповідні операції (якщо не поставлені дужки) виконуються в такій послідовності: заперечення, кон'юнкція, диз'юнкція, імплікація, эквіваленція.
Таблиці істинності насправді визначають логічні операції не тільки над елементарними висловленнями, але й над більш складними висловленнями. Таким чином, ми одержуємо можливість застосовувати логічні операції багаторазово, одержуючи з їх допомогою все більш складні висловлення.
Наприклад, складемо таблицю істинності наступного висловлення: ![]()
![]() В.
В.
|
№ |
А |
В |
|
|
|
1. |
1 |
1 |
0 |
1 |
|
2. |
1 |
0 |
0 |
0 |
|
3. |
0 |
1 |
1 |
1 |
|
4. |
0 |
0 |
1 |
1 |
Третій стовпчик таблиці заповнюється по першому на підставі таблиці істинності для заперечення, останній - по другому й третьому, з використанням таблиці істинності для диз'юнкції.
Порівняємо тепер отриману нами таблицю істинності висловлення ![]()
![]() В
В
с таблицею істинності для імплікації А![]() В.
В.
|
№ |
А |
В |
А |
|
1. |
1 |
1 |
1 |
|
2. |
1 |
0 |
0 |
|
3. |
0 |
1 |
1 |
|
4. |
0 |
0 |
1 |
|
№ |
А |
В |
|
|
1. |
1 |
1 |
1 |
|
2. |
1 |
0 |
0 |
|
3. |
0 |
1 |
1 |
|
4. |
0 |
0 |
1 |
Що ж бачимо, що висловлення ![]()
![]() В и А
В и А![]() В мають однакові таблиці істинності. Такі висловлення називаються рівносильними.
В мають однакові таблиці істинності. Такі висловлення називаються рівносильними.
Рівносильні висловлення прийнято з'єднувати знаком рівності. Отже, можна записати
А![]() В=
В=![]()
![]() В.
В.
В дійсності складні висловлення ![]()
![]() В и А
В и А![]() В мають різну форму: з елементарних висловлень А и В вони будуються за допомогою різних логічних операцій. Але для алгебри логіки істотно тільки одне: чи буде при певному розподілі значень істинності й хибності для елементарних висловлень складене з них складне висловлення істинним або хибним. У цьому смислі наші висловлення А
В мають різну форму: з елементарних висловлень А и В вони будуються за допомогою різних логічних операцій. Але для алгебри логіки істотно тільки одне: чи буде при певному розподілі значень істинності й хибності для елементарних висловлень складене з них складне висловлення істинним або хибним. У цьому смислі наші висловлення А![]() В и
В и ![]()
![]() В «однакові». Адже таблиці істинності складних висловлень А
В «однакові». Адже таблиці істинності складних висловлень А![]() В и
В и ![]()
![]() В однакові.
В однакові.
Розберемо ще один приклад.
Складемо таблицю істинності для висловлення (А![]() В)
В)![]() (
(![]()
![]()
![]() ).
).
|
№ |
А |
В |
А |
|
|
|
(А |
|
1. |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
|
2. |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|
3. |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|
4. |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
Третій стовпчик таблиці заповнюється по першим двох на підставі таблиці істинності для імплікації; четвертий і п'ятий - відповідно по другому й першому стовпчику на підставі таблиці істинності для заперечення. Шостий стовпчик складається по четвертому й п'ятому за допомогою таблиці істинності для імплікації, і, нарешті, останній сьомий стовпчик виписується по третьому й шостому відповідно до таблиці істинності для эквіваленції.
У результаті ми з вами одержали важливий результат: висловлення (А![]() В)
В)![]() (
(![]()
![]()
![]() ) істинно завжди, тобто при будь-якому наборі істинності й хибності складових його висловлень А и В. Такі висловлення називаються тотожньо-істинним. Позначають тотожно-щирі висловлення латинською літерою I. Правий стовпчик істинності такого висловлення суцільно заповнений 1, тому можна записати: (А
) істинно завжди, тобто при будь-якому наборі істинності й хибності складових його висловлень А и В. Такі висловлення називаються тотожньо-істинним. Позначають тотожно-щирі висловлення латинською літерою I. Правий стовпчик істинності такого висловлення суцільно заповнений 1, тому можна записати: (А![]() В)
В)![]() (
(![]()
![]()
![]() )=I.
)=I.
Якщо уважно подивитися на таблицю істинності, то можна помітити, що в ній стовпчики 3 і 6 збігаються, тобто таблиці істинності висловлень А![]() В и
В и ![]()
![]()
![]() однакові, і, отже, ці висловлення рівносильні,тобто А
однакові, і, отже, ці висловлення рівносильні,тобто А![]() В =
В = ![]()
![]()
![]() .
.
Поряд з тотожно-істинними висловленнями відзначимо висловлення тотожньо-хибні, тобто хибні завжди, незалежно від того, істинні або хибні складові їхнього висловлення. Правий стовпчик таблицю істинності такого висловлення суцільно заповнений 0. Позначають тотожно-хибні висловлення латинською літерою L.
 Ну, що спробуєте самі?
Ну, що спробуєте самі?
Завдання №1.
Складіть таблицю істинності складного висловлення:
-
А
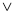 (
(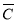
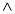 В);
В);
-
А
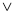 (В
(В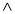 С
С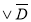 );
);
-
D
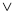 (B
(B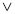 C)
C)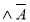 .
.
Завдання №2.
Складіть таблицю істинності складних висловлень і визначить серед них тотожньо-істинних й тотожньо-хибних висловлення:
-
В
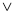 (А
(А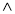
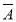 );
);
-
С
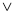 (В
(В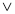
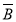 );
);
-
В
 (С
(С
 )
)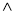 D.
D.
Завдання №3.
Доведіть або спростуйте рівносильність висловлень:
-
(А
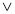 В)
В)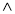 (А
(А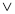 В
В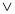 С)= А
С)= А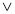 В;
В;
-
(А
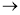 В)
В)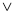 В =
В =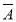
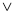 В;
В;
-
(А
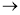 В)
В)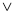 (А
(А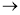 В)=
В)= 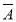
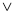 В
В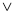 С;
С;
-
(А
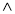 В)
В)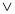 (
(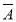
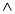 В)
В) 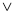 В = В
В = В
-
(А
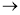 В)
В) 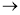 А =А;
А =А;
-
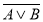
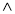 (А
(А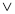 В
В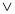 С)
С) 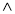 А = А.
А = А.
Завдання №4.
За допомогою побудови таблиць істинності доведіть, що:
-
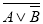 =
=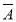
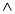 В;
В;
-
А
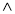 В= В
В= В 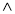 А ;
А ;
-
А
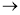 В=
В=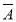
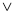 В;
В;
-
А
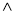 (
(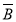
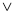 А)=А;
А)=А;
Завдання №5.
За допомогою таблиць істинності встановите, чи є тотожньо-
істинними або тотожньо-хибними наступні висловлення:
-
(А
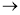 В)
В)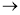 (В
(В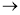 А);
А);
-
(А
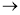 В)
В)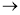 (А
(А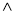
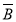
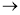 В);
В);
-
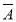
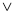 В
В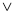 ( В
( В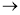 А);
А);
-
А
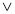 В
В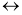
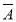
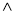 ( В
( В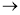
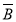 );
);
-
А
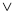
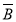
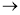
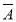 ;
;
-
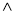 А
А 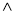 (А
(А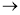 В).
В).
 3.9.Закони логіки.
3.9.Закони логіки.
Прийшов час підбити підсумок і сформулювати яким законам підкоряється логіка. Адже в кожної науки є свої закони, правила, аксіоми, за допомогою яких ми вивчаємо, доводимо, проводимо досліди.
Введемо позначення: I - тотожньо-істинні, а L - тотожньо-хибні висловлення.
Отже,
Закон виключення третього. А![]()
![]() =I
=I
Усяке висловлення або істинно, або хибне, третього не дано.
Закон протиріччя. А![]()
![]() =L
=L
Усяке висловлення не може бути одночасно істинним або хибним.
Закон заперечення.![]() =A
=A
Заперечення заперечення збігається з вихідним висловленням.
Легко перевіряються наступні равносильности - закони алгебри висловлень:
- Комуникативність диз'юнкції
А![]() В= В
В= В![]() А,
А,
- Комуникативність кон'юнкції
А![]() В= В
В= В![]() А,
А,
- Асоціативність диз'юнкції
А![]() (В
(В![]() С)= (А
С)= (А![]() В)
В)![]() С,
С,
- Асоціативність кон'юнкції
А![]() (В
(В![]() С)=( А
С)=( А![]() В)
В)![]() С,
С,
- Перший дистрибутивний закон
А![]() (В
(В![]() С)= (А
С)= (А![]() В)
В)![]() ( А
( А![]() С),
С),
- Другий дистрибутивний закон
А![]() (В
(В![]() С)= (А
С)= (А![]() В)
В)![]() ( А
( А![]() С),
С),
- Закони де Моргана
![]() =
=![]()
![]()
![]() ;
; ![]() =
=![]()
![]()
![]() ,
,
- Закон подвійного заперечення
![]() =A
=A
- Закон ідемпотентності
А![]() А=А; А
А=А; А![]() А=А,
А=А,
- Закони, що виражають тотожньо-істинні (I) і тотожньо-хибні
висловлення (L)
А![]()
![]() =I; А
=I; А![]()
![]() =L;
=L;
А![]() I=I; А
I=I; А![]() I=A;
I=A;
А![]() L=A; А
L=A; А![]() L=L;
L=L;
![]() =L.
=L.
Перші п'ять законів алгебра логіки аналогічні законам звичайної алгебри. Адже диз'юнкцію й кон'юнкцію можна замінити відповідно логічним додаванням і логічним множенням, що нерідко роблять, заміняючи при цьому знаки «![]() » і «
» і «![]() » звичайними знаками додавання «+» і множення «.».
» звичайними знаками додавання «+» і множення «.».
Розглянемо наступний приклад:
Спростити висловлення:
(А![]() В
В![]()
![]() )
)![]() (A
(A![]()
![]() )
)![]() (В
(В![]() С
С![]()
![]() ).
).
Тому що А![]() В
В![]()
![]() = А
= А![]() L=L, А
L=L, А![]()
![]() =L, В
=L, В![]() С
С![]()
![]() = В
= В![]() L=L,
L=L,
То наше висловлення рівносильне висловленню
L![]() L
L![]() L=L, тобто воно є тотожньо-хибним.
L=L, тобто воно є тотожньо-хибним.
 Завдання №1.
Завдання №1.
Сформулюйте твердження, які відповідно до законів де Моргана виражають те саме, що й наступні висловлення:
- Невірно, що число 9 - просте або парне;
- А не дорівнює 3 і В не дорівнює 2;
- Я не висплюся або спізнюся;
- Невірно, що кожне із чисел х и в - прості;
Завдання №2.
Спростите, якщо можливо, що висловлення:
-
А
 В
В А
А С;
С;
-
А
 В
В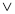
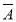
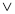 С;
С;
-
(А
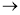 В)
В)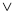
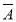 ;
;
-
(А
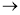 В)
В)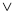 ( В
( В  А);
А);
-
А
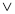 (A
(A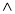 В
В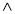 С);
С);
-
А
 (В
(В С
С А).
А).
Завдання №3.
Розв'яжіть задачу.
Брауна, Джона й Сміта звинуватили в співучасті в пограбуванні банку. Викрадачі зникли на автомобілі, який чекав їх. На слідстві Браун показав, що злочинці були на синьому «Б'юіку», Джон сказав, що це був чорний «Седан», а Сміт стверджував, що це був «Форд», і не в якому разі не синій. Стало відомо, що бажаючи заплутати слідство, кожний з них указав правильно або тільки марку машини, або тільки її колір. Якого кольору був автомобіль і якої марки?
Короткі теоретичні відомості.
Набір предметів або понять, зібраних забудь-якою ознакою, називають множина, а кожний із цих предметів - елемент множини.
Нескінченної множини називається рахунковим, якщо його елементи можна
перенумерувати натуральними номерами.
Якщо елементи нескінченної множини перенумерувати не можна, то воно незліченне.
Множина, що не має жодного елемента, називається порожньою множиною - ![]() .
.
Знак «є» позначає належність елемента даній множині.
Якщо кожний елемент множини В є елементом множини А , то множину В називають підмножиною множини А. В![]() А.
А.
Об'єднанням (сумою) множин А и В називають така множина С, що містить у собі всі елементи множини А и ті елементи множини В, яких немає в А.
С=А![]() В або С=А+В.
В або С=А+В.
Перерізом (добутком) множин А и В називають таку множину С, що складається із спільних елементів множин А и В.
С=А![]() В або С=А.В.
В або С=А.В.
Доповненням множини А до множини В називають таку множину С, для якої виконуються умови: : 1) А![]() З=В; 2) A
З=В; 2) A![]() З=
З=![]() .
.
Граф - це фігура, що складається із точок, з'єднаних між собою відрізками, кривими лініями або дугами.
Точки називаються вершинами графа, а лінії, що з'єднують вершини - ребрами.
Якщо ребро з'єднує дві вершини, то кажуть, що воно їм інцидентно.
Вершини, з'єднані ребром, називаються суміжними.
Дві вершини, що з'єднуються ребром, можуть збігатися; таке ребро називається петлею.
Вершина, з якої виходить тільки одне ребро, називається висяча вершина.
Вершина, що не належить ребрам, називається ізольована вершина.
Граф, що складається з ізольованих вершин, називається нуль-граф.
Граф, у якому кожна пара вершин з'єднана ребром, називається повним графом.
Циклом (або ейлеровим шляхом) називається шлях, що з'єднує по одному разі всі ребра.
Граф, що володіє циклом, називають ейлеровим.
Якщо вершини виходить непарне число ребер, то її називають непарною, якщо ж виходить парне число ребер, то - парною.
Кількість ребер, що виходять із однієї вершини, називають степенем вершини.
Граф можна намалювати, не відриваючи олівець від паперу й проводячи по кожному ребру тільки один раз, якщо всієї його вершини парні, при цьому починати можна в будь-якій вершині й закінчити теж у кожній.
Граф тільки із двома непарними вершинами можна накреслити тільки одним розчерком, при цьому починати треба в одній непарній вершині, а закінчувати - в іншій непарній вершині.
Ці два твердження називаються теоремами Ейлера, графи, які їм підкоряються, називаються ейлеровими або унікурсальними (одноколійними).
Теорема парності: число непарних вершин будь-який граф парне.
Кількість ребер будь-якого графа можна знайти, склавши степені вершин, і отриманий результат поділити на два.
Граф називається зв'язаним, якщо будь-які дві його вершини з'єднані послідовністю ребер, кожне наступне з яких починається наприкінці попереднього.
Замкнутий шлях (цикл)- це шлях, початок і кінець, якого збігаються.
Простий шлях - це шлях, у якому ніяке ребро не зустрічається двічі. Дерево - зв'язний граф, у якого немає циклів.
Позначимо число вершин дерева буквою V, число ребер - буквою E. Тоді одержимо теорему: У дереві число вершин на одиницю більше числа ребер. V-E=1
Граф, якому можна намалювати так, щоб його ребра не перетиналися ніде крім вершин, називають плоским графом.
Дерево - це плоский граф.
Плоский граф ділить площину, на якій він намальований, на частині.
Позначимо: F - кількість частин площини;
V - кількість вершин графа;
E - кількість його ребер.
Тоді виконується наступна теорема: якщо плоский граф намальований правильно, те виконується умова: V-E+F=2.
Два графи називаються ізоморфними, якщо в них порівну вершин ( по n), і вершини кожного графа можна занумерувати числами від 1 до n так, щоб вершини першого графа були з'єднані ребрами тоді й тільки тоді, коли з'єднані ребрами відповідні ( занумерованими тими ж числами) вершини другого графа.
Усяке твердження, щодо якого має сенс казати, що воно істинне або хибне, називається висловленням.
Логічна операція, що відповідає логічному зв'язуванню «не», «невірно, що» називається запереченням.
Закон виключення третього: Якщо дане твердження істинне, то його заперечення хибне, і навпаки, якщо дане твердження хибне, то його заперечення істинно.
Щоб побудувати заперечення висловлення вигляду «Всі Х мають властивість А», достатнє слово «всі» (або його синонім) замінити словом «деякі» (або його синонімом) і утворити заперечення твердження, що коштує за цим словом.
Щоб побудувати заперечення висловлення «Деякі Х мають властивість А» достатнє слово «деякі» (або його синонім) замінити словом «всі» (або його синонімом) і утворити заперечення твердження, що коштує за цим словом.
Кон'юнкціей (або логічним добутком) висловлень А и В називається висловлення «А и В», що істинно тоді й тільки тоді, коли А істинно й В істинно.
Диз'юнкцією називається операція, що кожним двом елементарним висловленням А и В ставить у відповідність нове висловлення «А або В», яке хибне тоді, коли хибні складені висловлення А и В. У всіх інших випадках висловлення «А або В» істинно.
Імплікацією висловлень А и В називається висловлення «якщо А\ те В», що хибне тільки тоді, коли, А істинно, а В хибне. У всіх інших випадках висловлення «якщо А, те В» істинно.
Якщо А и В два елементарних висловлення, то еквіваленціею висловлень А и В називається висловлення «А тоді й тільки тоді, коли В», що істинно тільки за умови, що висловлення А и В однакової істинності (тобто обоє істинні або обоє хибні).
Висловлення, що істинно завжди, тобто при будь-якому наборі істинності й хибності складових його висловлень А и В, називаються тотожньо-істинними.
Тотожньо-хибні висловлення, тобто хибні завжди, незалежно від того, істинні або хибні складові їхнього висловлення.
Закон виключення третього. А![]()
![]() =I
=I
Усяке висловлення або істинно, або хибне, третього не дано.
Закон протиріччя. А![]()
![]() =L
=L
Усяке висловлення не може бути одночасно істинним або хибним.
Закон заперечення.![]() =A
=A
Заперечення заперечення збігається з вихідним висловленням.
Легко перевіряються наступні рівносильності - закони алгебри висловлень:
Комуникативність диз'юнкції
А![]() В= В
В= В![]() А,
А,
Комуникативність кон'юнкції
А![]() В= В
В= В![]() А,
А,
Асоціативність диз'юнкції
А![]() (В
(В![]() С)= (А
С)= (А![]() В)
В)![]() С,
С,
Асоціативність кон'юнкції
А![]() (В
(В![]() С)=( А
С)=( А![]() В)
В)![]() С,
С,
Перший дистрибутивний закон
А![]() (В
(В![]() С)= (А
С)= (А![]() В)
В)![]() ( А
( А![]() С),
С),
Другий дистрибутивний закон
А![]() (В
(В![]() С)= (А
С)= (А![]() В)
В)![]() ( А
( А![]() С),
С),
Закони де Моргана
![]() =
=![]()
![]()
![]() ;
; ![]() =
=![]()
![]()
![]() ,
,
Закон подвійного заперечення
![]() =A
=A
Закон ідемпотентності
А![]() А=А; А
А=А; А![]() А=А,
А=А,
Закони, що виражають тотожно-істинні (I) і тотожньо-хибні висловлення (L)
А![]()
![]() =I; А
=I; А![]()
![]() =L;
=L;
А![]() I=I; А
I=I; А![]() I=A;
I=A;
А![]() L=A; А
L=A; А![]() L=L;
L=L; ![]() =L.
=L.
1
-
Дякую!
-
-
Дякую, що виклали матеріал у мережу!


про публікацію авторської розробки
Додати розробку

