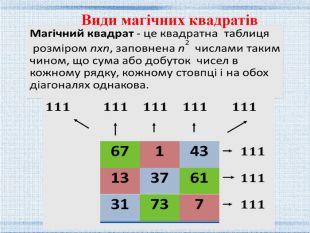
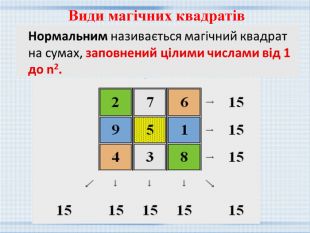
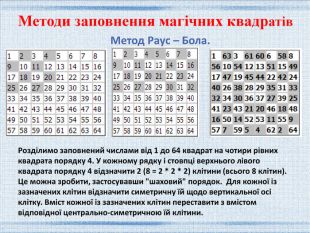
Магічні квадрати та їх застосування.

Магічні квадрати. Творчо-пошукова робота Прохорчука Дмитра учня 8 класу,КЗШ № 123

Мета дослідження: з'ясувати різні способи складання магічних квадратів і вивчити області їх застосування. Завдання дослідження:-познайомитися з історією появи магічних квадратів;-з'ясувати види магічних квадратів і способи їх заповнення;-познайомитися з ученими, які вивчали магічні квадрати.-провести дослідження твердження Піфагора про те, що доля людини залежить від числа його народження;-виявити сфери застосування магічних квадратів.-познайомитися ближче з популярною грою судоку. Предмет дослідження: процес розвитку теорії магічних квадратів, властивості, методи складання магічних квадратів. Проблемне питання: чому квадрат названий магічним, в чому його магічні властивості?Гіпотеза: Я думаю, що існують способи заповнення магічних квадратів, вивчивши які можна скласти магічний квадрат будь-якого порядку.

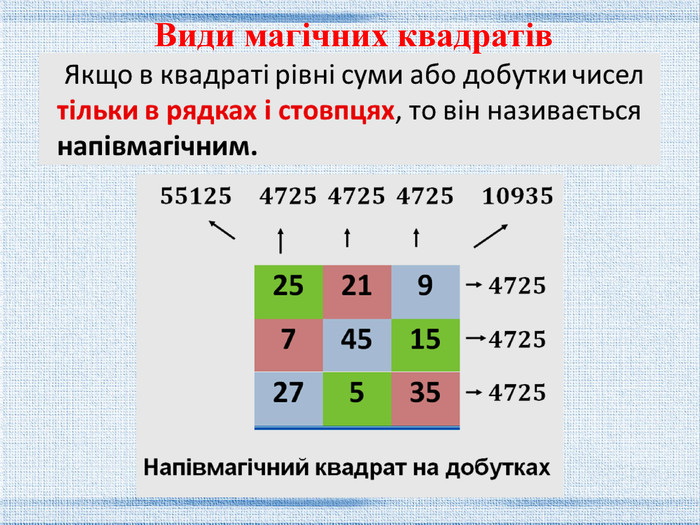
Магічні квадрати… Від цього словосполучення відразу віє чарами. Великі вчені давнини вважали кількісні відносини основою сутності світу. Тому числа і їх співвідношення займали найбільші розуми людства. Однією з найцікавіших математичних головоломок вважаються магічні квадрати. Магічні квадрати

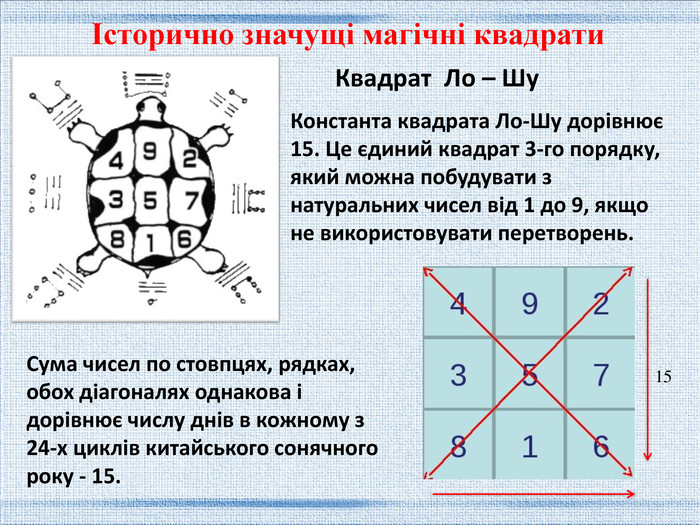
Перші згадки про магічні квадрати були у давніх китайців. Згідно з легендою, за часів правління імператора Ю (бл. 2200 до н.е.) з вод Хуанхе (Жовтої ріки) спливла священна черепаха, на панцирі якої були написані таємничі ієрогліфи і ці знаки відомі під назвою ло-шу і рівносильні магічному квадрату. Історія появи магічних квадратів

Перший магічний квадрат з трьома клітинами в основі був описаний в арабському манускрипті кінця восьмого століття, де згадувався його автор - грецький філософ-неопіфагорієць Аполлоній Тіанський. А перший твір про магічні квадрати було написано візантійським граматистом і лексикографом Мануелем Мосхопулосом (XIII-XIV ст.). У трактаті "Повчання по знаходженню числових квадратів" (приблизно 1300 р.). Історія появи магічних квадратів

Карл Фридрих Гаусс. П’єр Ферма Блез Паскаль. Міхаель Штіфель. Леонард Ейлер. Вчені, які вивчали математичні квадрати

На початку XVI століття про квадрат з магічним числом 34 дізнався знаменитий німецький художник Альфред Дюрер (1471 - 1528 рр.). Він був їм так зачарований, що навіть відтворив його в одній зі своїх гравюр ( «Меланхолія», 1514 р.). Магічні квадрати в мистецтві

В 1533 р. німецький гуманіст Генріх Корнелій Агріппа (1486 - 1535 рр.) З Неттенхейма в своєму творі «Про потаємну філософію» описав сім магічних квадратів, що мають в основі 3, 4, 5, 6, 7, 8 і 9 клітин. Число квадратів було вибрано рівним числу птолемеєвих планетних сфер. Історія розвитку магічних квадратів

У вивченні магічних фігур стартовою точкою стала Монада. Піфагорійці уявляли Монаду фігурою, що складається з десяти точок - вузлів. Ці десять вузлів, названі Тетрактіс, утворюють дев'ять рівносторонніх трикутників, які уособлюють повноту всесвітньої порожнечі і Животворящий хрест. Історія розвитку магічних квадратів

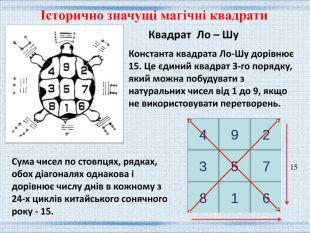
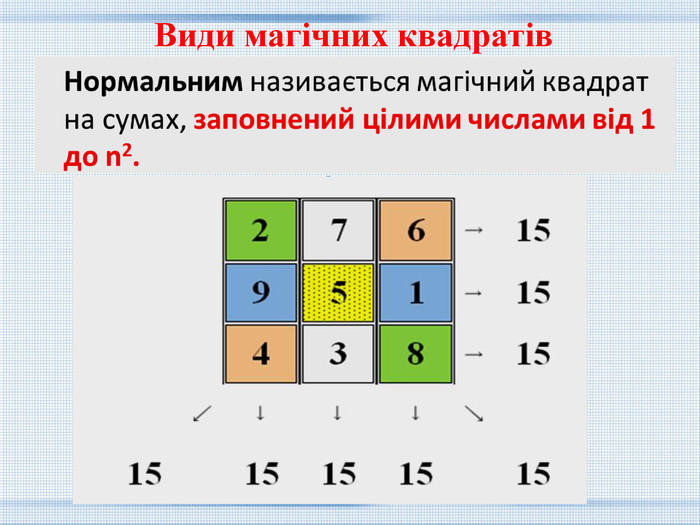
Константа квадрата Ло-Шу дорівнює 15. Це єдиний квадрат 3-го порядку, який можна побудувати з натуральних чисел від 1 до 9, якщо не використовувати перетворень. Квадрат Ло – Шу. Сума чисел по стовпцях, рядках, обох діагоналях однакова і дорівнює числу днів в кожному з 24-х циклів китайського сонячного року - 15. 15Історично значущі магічні квадрати

Історично значущі магічні квадрати

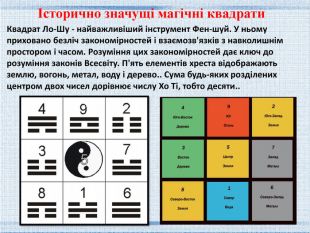
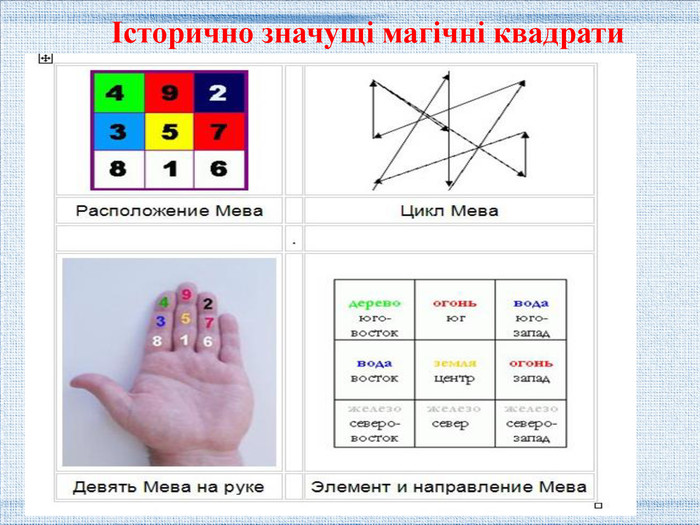
Квадрат Ло-Шу - найважливіший інструмент Фен-шуй. У ньому приховано безліч закономірностей і взаємозв'язків з навколишнім простором і часом. Розуміння цих закономірностей дає ключ до розуміння законів Всесвіту. П'ять елементів хреста відображають землю, вогонь, метал, воду і дерево.. Сума будь-яких розділених центром двох чисел дорівнює числу Хо Ті, тобто десяти..Історично значущі магічні квадрати

Квадрат на гравюрі володіє цікавими додатковими властивостями: сума чисел, розташованих по його кутах, дорівнює магічному числу 34; суми чисел у кожному з п'яти маленьких квадратів (у чотири клітини), що примикають до вершин даного квадрата, і в такому ж центральному квадраті теж рівні 34; Квадрат Дюрерав кожному його рядку є пара чисел, сума яких дорівнює 15;якщо скласти чотири числа, отримані ходом шахового коня - буде 34.Історично значущі магічні квадрати

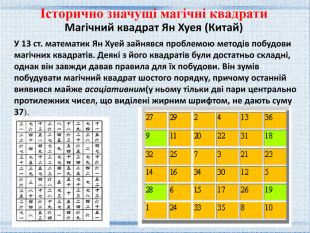
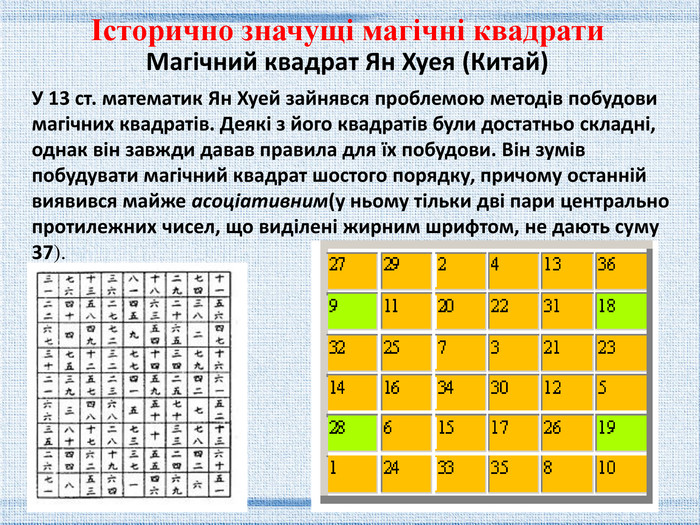
Магічний квадрат Ян Хуея (Китай)У 13 ст. математик Ян Хуей зайнявся проблемою методів побудови магічних квадратів. Деякі з його квадратів були достатньо складні, однак він завжди давав правила для їх побудови. Він зумів побудувати магічний квадрат шостого порядку, причому останній виявився майже асоціативним(у ньому тільки дві пари центрально протилежних чисел, що виділені жирним шрифтом, не дають суму 37). Історично значущі магічні квадрати

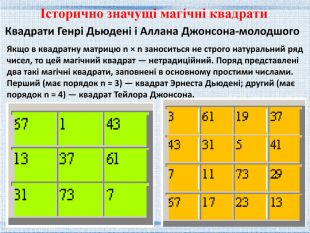
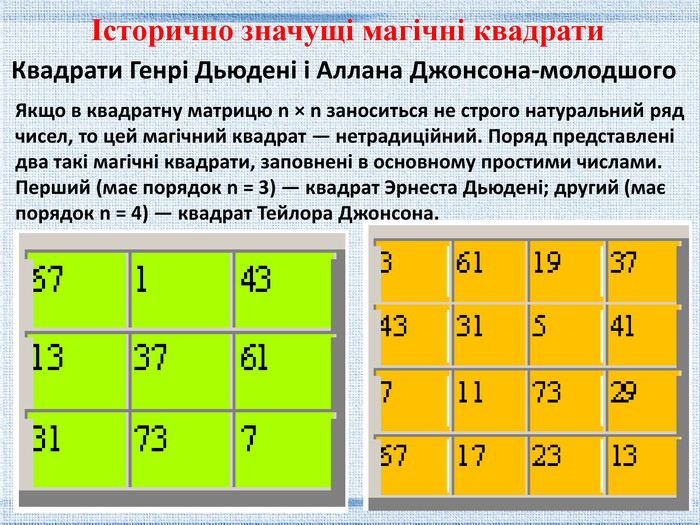
Квадрати Генрі Дьюдені і Аллана Джонсона-молодшого. Якщо в квадратну матрицю n × n заноситься не строго натуральний ряд чисел, то цей магічний квадрат — нетрадиційний. Поряд представлені два такі магічні квадрати, заповнені в основному простими числами. Перший (має порядок n = 3) — квадрат Эрнеста Дьюдені; другий (має порядок n = 4) — квадрат Тейлора Джонсона. Історично значущі магічні квадрати

Квадрат, побудований в 1913 році Дж. Н. Мансі, примітний тим, що він складений з 143 послідовних простих чисел за винятком двох моментів: залучена одиниця, яка не є простим числом, і не використано єдине парне просте число — 2. Квадрат Дж. Н. МансіІсторично значущі магічні квадрати

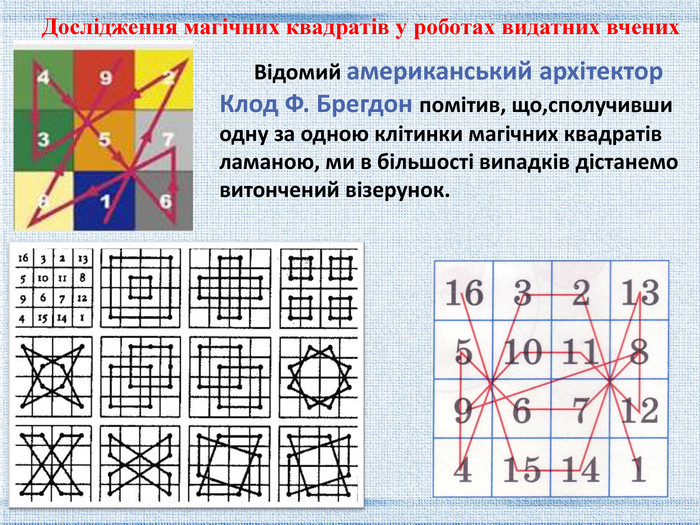
Необхідно розмістити 16 гральних карт з тузів, королів, дам і валетів всіх чотирьох мастей у вигляді квадрата так, щоб всі масті і карти всіх достоїнств зустрічалися в кожному рядку і в кожному стовпці рівно один раз. Це завдання має 6192 рішення (якщо додатково вимагати, щоб і діагоналі квадрата задовольняли тій же умові, то число рішень зменшиться в 6 разів і стане рівним тисячі сто п'ятьдесят два). Латинські квадрати. Задача Жака Озанами. Дослідження магічних квадратів у роботах видатних вчених

Вчений сформулював «завдання про 36 офіцерів»: Необхідно розмістити 36 офіцерів шести різних полків і шести різних військових звань в каре так, щоб в кожній колоні і в кожному ряду був рівно один офіцер кожного полку і кожного військового звання. Латинські квадрати Ейлера. Ейлер не зміг знайти розв’язання цієї задачі, утворивши квадрат лише для 25 офіцерів. Дослідження магічних квадратів у роботах видатних вчених

Відомий американський архітектор Клод Ф. Брегдон помітив, що,сполучивши одну за одною клітинки магічних квадратів ламаною, ми в більшості випадків дістанемо витончений візерунок. Дослідження магічних квадратів у роботах видатних вчених

Види магічних квадратів

Види магічних квадратів

Види магічних квадратів

Види магічних квадратів

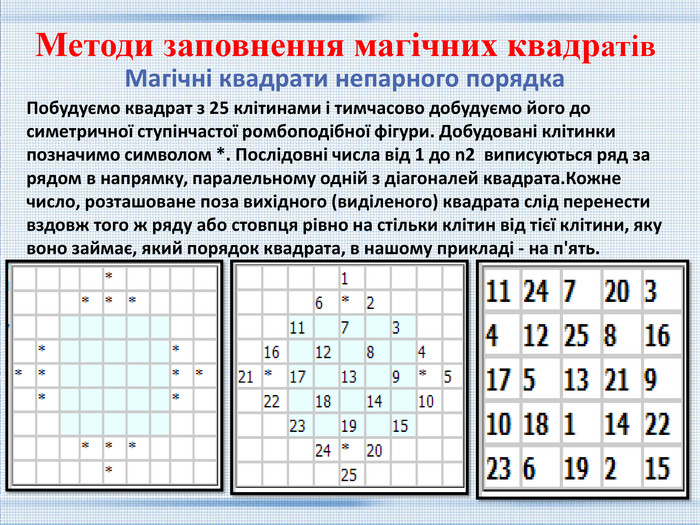
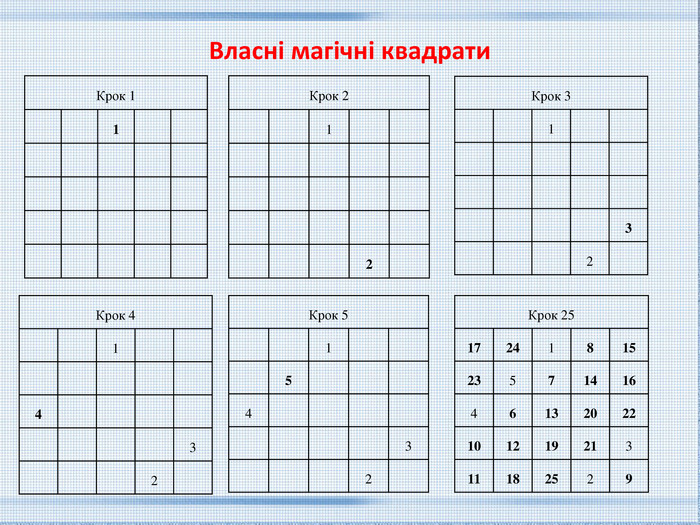
Магічні квадрати непарного порядка. Методи заповнення магічних квадратів. Побудуємо квадрат з 25 клітинами і тимчасово добудуємо його до симетричної ступінчастої ромбоподібної фігури. Добудовані клітинки позначимо символом *. Послідовні числа від 1 до n2 виписуються ряд за рядом в напрямку, паралельному одній з діагоналей квадрата. Кожне число, розташоване поза вихідного (виділеного) квадрата слід перенести вздовж того ж ряду або стовпця рівно на стільки клітин від тієї клітини, яку воно займає, який порядок квадрата, в нашому прикладі - на п'ять.

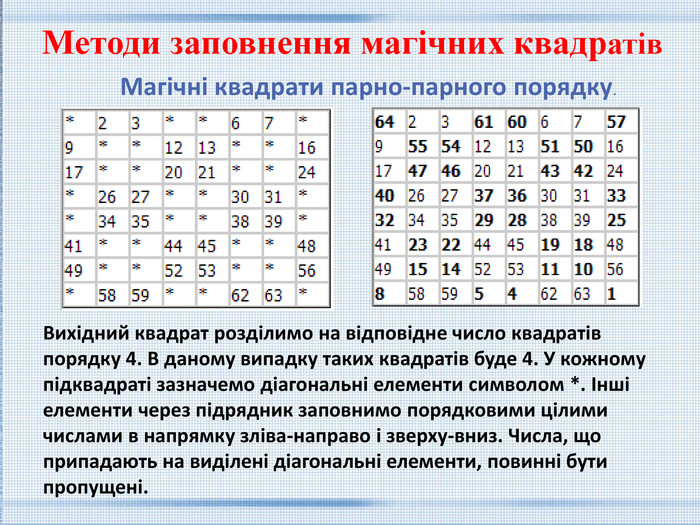
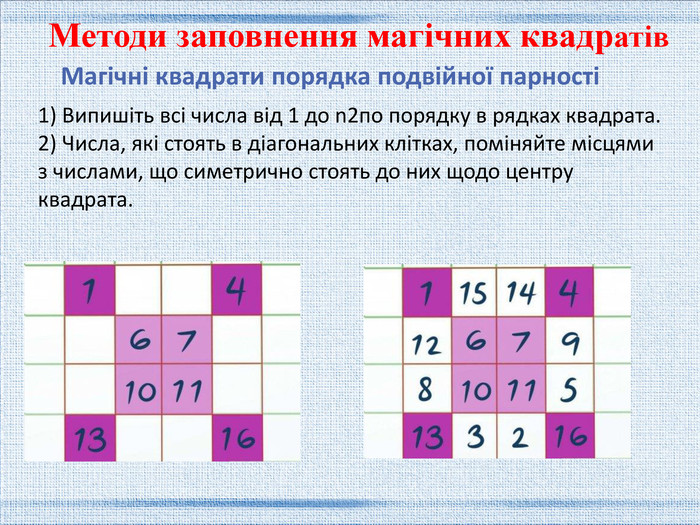
Магічні квадрати парно-парного порядку. Вихідний квадрат розділимо на відповідне число квадратів порядку 4. В даному випадку таких квадратів буде 4. У кожному підквадраті зазначемо діагональні елементи символом *. Інші елементи через підрядник заповнимо порядковими цілими числами в напрямку зліва-направо і зверху-вниз. Числа, що припадають на виділені діагональні елементи, повинні бути пропущені. Методи заповнення магічних квадратів

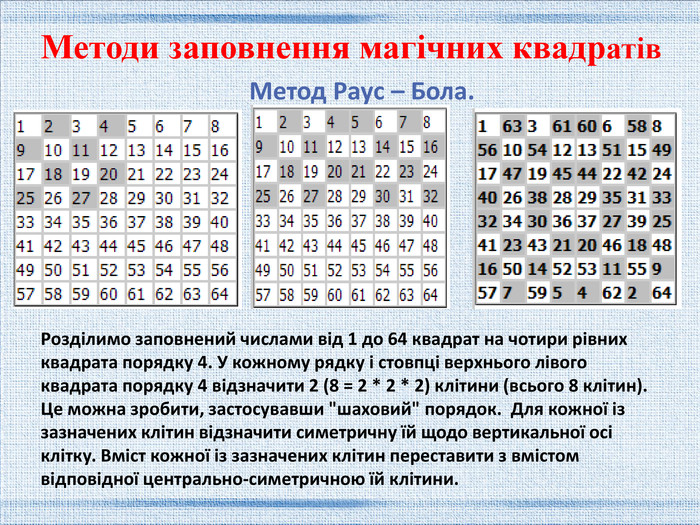
Метод Раус – Бола. Методи заповнення магічних квадратів. Розділимо заповнений числами від 1 до 64 квадрат на чотири рівних квадрата порядку 4. У кожному рядку і стовпці верхнього лівого квадрата порядку 4 відзначити 2 (8 = 2 * 2 * 2) клітини (всього 8 клітин). Це можна зробити, застосувавши "шаховий" порядок. Для кожної із зазначених клітин відзначити симетричну їй щодо вертикальної осі клітку. Вміст кожної із зазначених клітин переставити з вмістом відповідної центрально-симетричною їй клітини.

Магічні квадрати парно-непарного порядку. Методи заповнення магічних квадратів. Розділимо заповнений числами від 1 до 100 квадрат на чотири квадрати близько 5 осями симетрії. У лівому верхньому квадраті зафарбовані різним кольором три групи клітиню. Однаковим кольором виділимо клітини, розташовані уздовж діагоналі квадрата і прямих, їй паралельних. Число, що стоїть в кожній із зазначених в пункті 2 клітин, переставимо з числом з відповідною центрально-симетричною клітини. Вміст кожної клітини другої групи обміняю з вмістом симетричною їй відносно горизонтальної осі клітини. Вміст кожної клітини другої групи обміняю з вмістом симетричною їй відносно горизонтальної осі клітини. Вміст кожної клітини третьої групи обміняю з вмістом симетричною їй щодо вертикальної осі клітини.

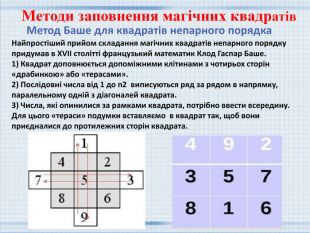
Метод Баше для квадратів непарного порядка. Найпростіший прийом складання магічних квадратів непарного порядку придумав в XVII столітті французький математик Клод Гаспар Баше.1) Квадрат доповнюється допоміжними клітинами з чотирьох сторін «драбинкою» або «терасами».2) Послідовні числа від 1 до n2 виписуються ряд за рядом в напрямку, паралельному одній з діагоналей квадрата.3) Числа, які опинилися за рамками квадрата, потрібно ввести всередину. Для цього «тераси» подумки вставляємо в квадрат так, щоб вони приєдналися до протилежних сторін квадрата. Методи заповнення магічних квадратів

Магічні квадрати порядка подвійної парності1) Випишіть всі числа від 1 до n2по порядку в рядках квадрата.2) Числа, які стоять в діагональних клітках, поміняйте місцями з числами, що симетрично стоять до них щодо центру квадрата. Методи заповнення магічних квадратів

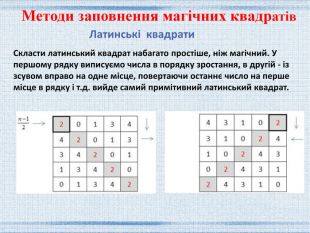
Латинські квадрати. Скласти латинський квадрат набагато простіше, ніж магічний. У першому рядку виписуємо числа в порядку зростання, в другій - із зсувом вправо на одне місце, повертаючи останнє число на перше місце в рядку і т.д. вийде самий примітивний латинський квадрат. Методи заповнення магічних квадратів

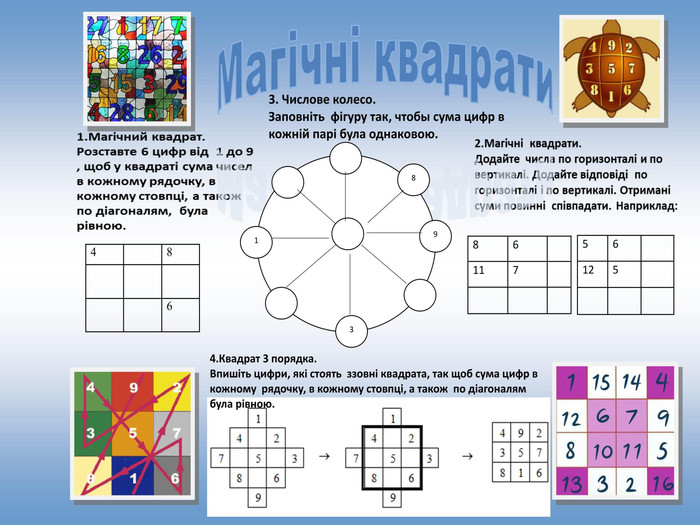
Застосування магічних квадратів. Судоку. Правила дуже прості: є квадрат з 81 клітини, який в свою чергу складається з 9 квадратів по 9 клітин. Потрібно розставити в клітинах числа від 1 до 9 так, щоб в кожному рядку і стовпці великого квадрата, а також всередині кожного з малих квадратів числа не повторювалися. Какуро. Ваша мета - вписати цифри від 1 до 9 в усі осередки поля відповідно до даних підказками. Цифри в спеціальних осередках вказують суму, яку ви повинні скласти з внесених цифр. Цифри в одній комірці не повинні повторюватися! У горизонтальних осередках цифри повинні бути розташовані по зростанню, в вертікальних- спаданням.

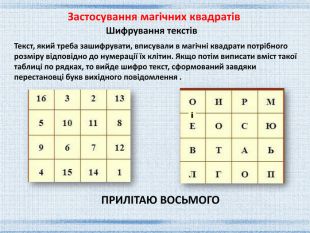
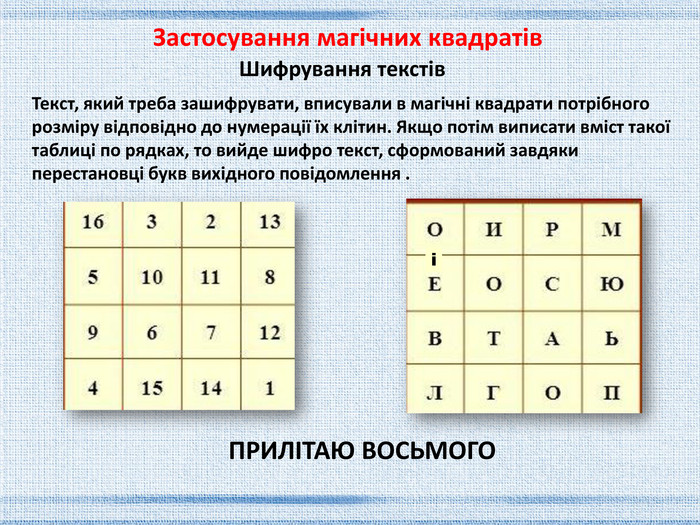
Текст, який треба зашифрувати, вписували в магічні квадрати потрібного розміру відповідно до нумерації їх клітин. Якщо потім виписати вміст такої таблиці по рядках, то вийде шифро текст, сформований завдяки перестановці букв вихідного повідомлення . Шифрування текстівіПРИЛІТАЮ ВОСЬМОГОЗастосування магічних квадратів

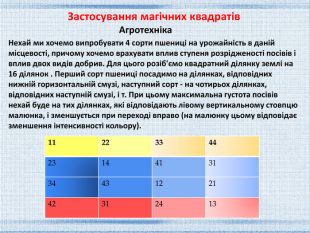
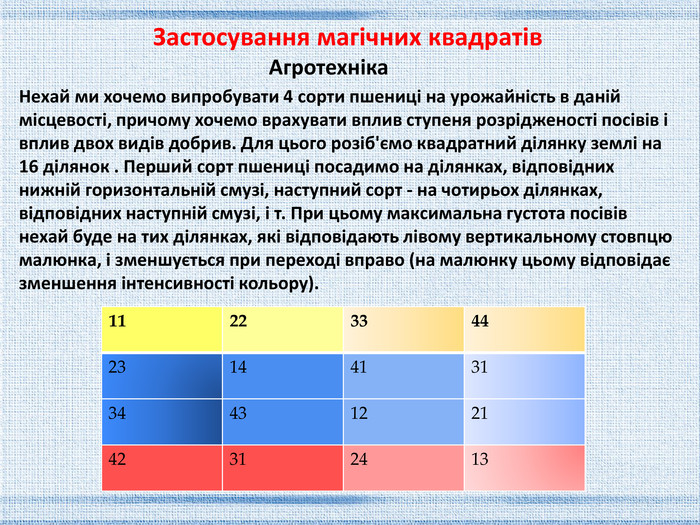
Нехай ми хочемо випробувати 4 сорти пшениці на урожайність в даній місцевості, причому хочемо врахувати вплив ступеня розрідженості посівів і вплив двох видів добрив. Для цього розіб'ємо квадратний ділянку землі на 16 ділянок . Перший сорт пшениці посадимо на ділянках, відповідних нижній горизонтальній смузі, наступний сорт - на чотирьох ділянках, відповідних наступній смузі, і т. При цьому максимальна густота посівів нехай буде на тих ділянках, які відповідають лівому вертикальному стовпцю малюнка, і зменшується при переході вправо (на малюнку цьому відповідає зменшення інтенсивності кольору). Агротехніка{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}11223344231441313443122142312413 Застосування магічних квадратів

Цифри ж, які стоять в клітинах малюнка, нехай означають: Перший - Кількість кілограмів добрива першого виду, внесеного на цю ділянку, а друга - кількість вноситься добрива другого виду. Неважко зрозуміти, що при цьому реалізовані всі можливі пари сполучень як сорти і густоти посіву, так і інших компонентів: сортів і добрив першого виду, добрив першого і другого видів, густоти і добрив другого виду. Використання ортогональних латинських квадратів допомагає врахувати всі можливі варіанти в експериментах в сільському господарстві, фізики, хімії, техніці. Застосування магічних квадратів

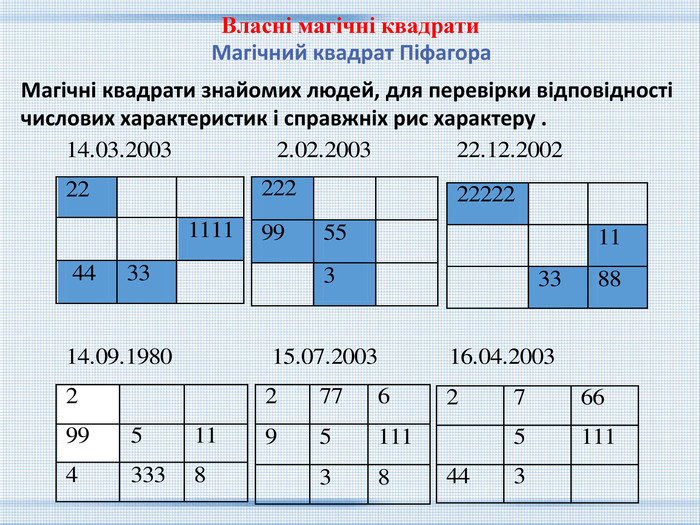
Великий вчений Піфагор, вважав, що всім на світі керують числа. Тому сутність людини полягає теж в числі - даті народження. Він створив метод побудови квадрата, по якому можна пізнати характер людини, стан його здоров'я і його потенційні можливості, розкрити переваги і недоліки і тим самим виявити, що слід зробити для його вдосконалення Магічний квадрат Піфагора {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 1 характер 4 здоров’я 7 здібності 2 енергія 5 інтуіція 8 обов’язок 3 точність 6 праця 9 мудрість

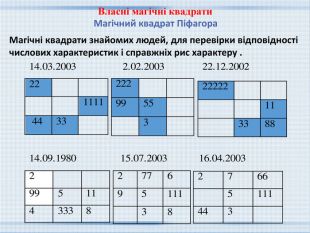
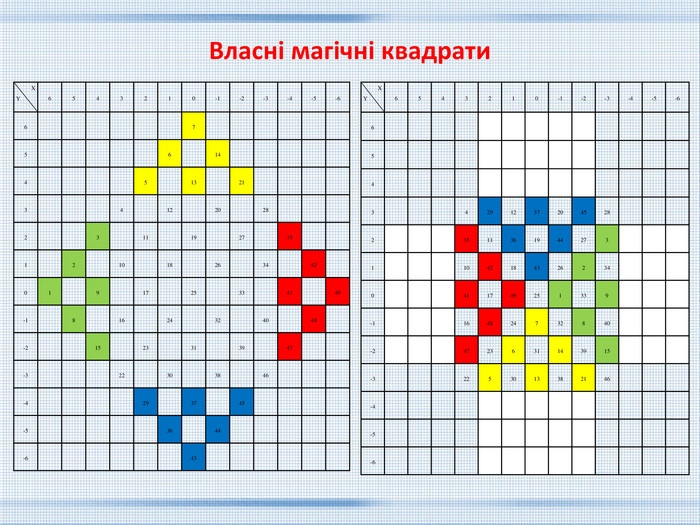
{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}11144-222255---99 Моя дата народження 20.12.2002. Складемо цифри дня, місяця і року народження (без урахування нулів): 2 + 1 + 2 + 2 + 2 = 9. Далі складаємо цифри результату: 0 + 9 = 9. Потім з першої суми віднімаємо подвоєну першу цифру дня народження: 9-4 = 5. І знову складаємо цифри останнього числа:0 + 5 = 3. Залишилося зробити останні складання - 1-й і 3-й і 2-й і 4-й сум: 9 + 5 = 14, 9 + 5 = 14. Отримали числа 20.12.2002, 9, 9, 5, 5, 14, 14 і складаємо магічний квадрат так, щоб всі одиниці цих чисел увійшли в клітинку 1, все двійки - в клітинку 2 і т. д. Власні магічні квадрати Магічний квадрат Піфагора

Магічні квадрати знайомих людей, для перевірки відповідності числових характеристик і справжніх рис характеру . Власні магічні квадрати Магічний квадрат Піфагора

Результати анкетування

Власні магічні квадрати. XY6543210-1-2-3-4-5-66             5             4             3   4291237204528   2   3511361944273   1   1042184326234   0   411749251339   -1   164824732840   -2   4723631143915   -3   2253013382146   -4             -5             -6             XY6543210-1-2-3-4-5-66      7      5     6 14     4    5 13 21    3   4 12 20 28   2  3 11 19 27 35  1 2 10 18 26 34 42 01 9 17 25 33 41 49-1 8 16 24 32 40 48 -2  15 23 31 39 47  -3   22 30 38 46   -4    29 37 45    -5     36 44     -6      43      

Крок 1  1                      Крок 2  1                    2 Крок 4  1       4        3   2 Крок 5  1   5   4        3   2 Крок 2517241815235714164613202210121921311182529 Крок 3  1                3   2 Власні магічні квадрати

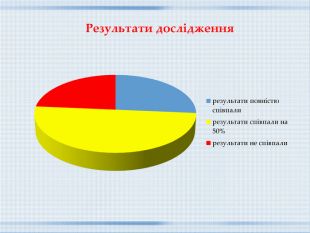
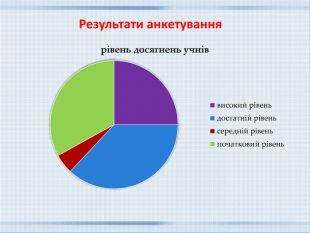
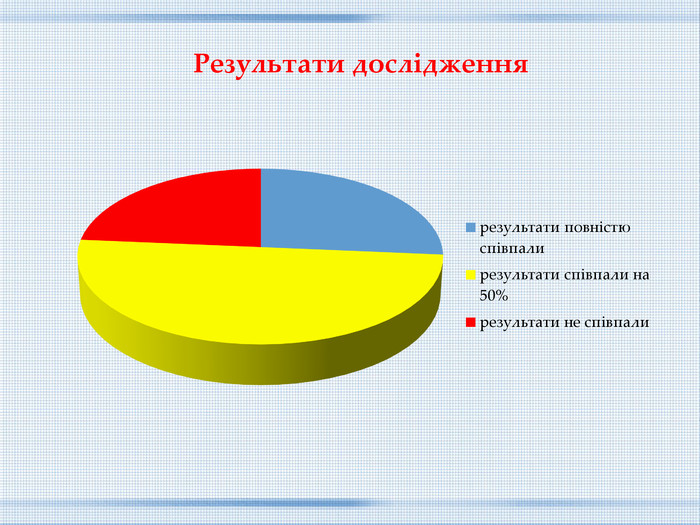
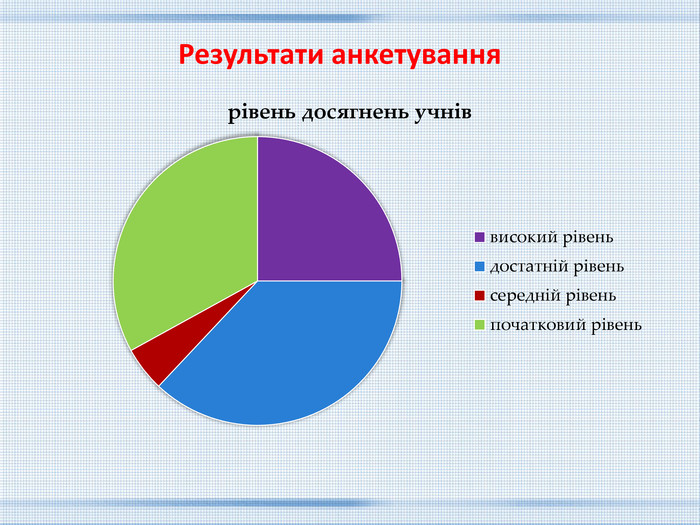
ВИСНОВОКУ цій роботі були розглянуті магічні квадрати, їх властивості та способи побудови. Окрім цього я дізнався, що: Магічні квадрати були відомі ще давнім математикам. Існують різні способи побудови магічних квадратів . Магічний квадрат Піфагора не завжди дає абсолютно вірну інформацію. Властивості магічних квадратів використовують в багатьох сферах нашого життя. Досліджуючи магічний квадрат Піфагора, ми зробили такий висновок: не слід сліпо вірити усьому магічному. Може бути деякі риси вдачі і закладені в даті народження людини, але людина завжди може знайти способи щось змінити у своїй долі. Результати роботи можна використовувати на уроках математики, математичного гуртка, підготовці до олімпіад і інтелектуальних змагань з математики.

ДЯКУЮ ЗА УВАГУ !