Математична гра "Брейн - ринг"

Заняття математикою – це така гімнастика для  розуму, для якої потрібна вся гнучкість і витривалість молодості  

Вінер

Правила гри.

У грі беруть участь три  команди по 6-10 гравців.  Дві команди займають місце за двома гральними столами. Ведучий зачитує умову задачі, а його  помічники роздають текст задачі обом командам. На розв’язування задачі відводиться не більше 2 хв. Команда, яка першою розв’язала задачу, подає знак ( підіймає прапорець  або дає сигнал свистком, або дитячим мелодійним молоточком) і дає відповідь, що оцінюється в 1 бал. Якщо відповідь не вірна, можливість відповісти має інша команда, а якщо не прозвучала відповідь, слово має третя команда і за правильну відповідь третя команда отримує 2 бали. У першій грі беруть участь  дві команди , які визначились по жеребкуванню, а в другій і наступних – команда, що перемогла і команда, яка відпочивала.

ПЕРША ГРА

1. Чому дорівнює половина  однієї сотої?   (0,005)
2. Сума двох чисел дорівнює 462. Одне з них закінчується на 0. Якщо цей нуль закреслити, то одержимо друге число. Знайдіть ці числа.   (420    і  42)
3. Я мешкаю на 6 поверсі, а мій друг на 3 поверсі того ж будинку. Повертаючись зі школи до дому, я долаю 60 сходинок. Скільки сходинок долає мій друг, коли повертається додому?    (24)
4. Назвіть наступне число в послідовності:  1,  1,  2,  3,  5,  8,  13,  …   (21)
5. Обчислити суму: 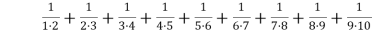  (  9/10)

ДРУГА ГРА

1. Знайдіть останню цифру в записі числа 6²⁰¹¹      (6)
2. Дві цукерки мають масу 10 г. яку масу має кілограм таких цукерок?  (1кг)
3. Скільки простих чисел знаходиться  в інтервалі між числами  -2,09  і  15,3?    (6 чисел 2, 3, 5, 7, 11, 13)
4. У скільки разів збільшиться двоцифрове число, якщо до нього дописати поруч таке саме число?     (у 101 раз)
5. Ціна на картоплю збільшилась на 20%. Через деякий час вона зменши-                     лась на 20%. Як змінилася початкова ціна на картоплю?                                         (знизилась на 4%)

ТРЕТЯ ГРА

1. Замість того, щоб додати число 23, мій друг відняв його. Яка різниця між правильним результатом і тим, що дістав мій товариш?    (46)
2. Чи буде число 555 555 точним квадратом натурального числа?    (Ні)
3. У класі 25 учнів. Скільки з них обов’язково народилося в один і той же             місяць?   (Троє)
4. П’ятеро друзів потиснули один одному руки. Скільки всього рукостискань  було зроблено? (10)
5. Кодом для відмикання сейфа є трицифрове число, що складається з різних цифр.       Скільки різних кодів можна скласти з цифр 1,  3,  5 ?   (6)

ЧЕТВЕРТА ГРА

1. З однієї купки переклали 6 зошитів до іншої. У результаті зошитів стало порівну. На скільки більше було зошитів у першій купці, ніж у другій?  ( На 12)
2. З коробки, у якій  лежить 8 червоних 1 6 синіх олівців, навмання витягують олівці. Яку найменшу кількість олівців треба витягнути, щоб  серед них було не менше ніж два червоних і неменше ніж три синіх?  ( 11)
3. Було 9 аркушів паперу. Деякі з них розірвали на три частини. Після  цього  стало 15 аркушів. Скільки аркушів було розірвано?   (3)
4. Скільки годин становить половина від третини від четвертини доби?  (1 год)
5. Чи може сума трьох послідовних натуральних чисел  бути простим числом?   (Ні.   а+1+а+2+а+3= 3а+3=3(а+1)  )

П'ЯТА ГРА

1. Скільки секунд містить чверть години?  (900с)
2. Іван купив деякий товар за 7 грн, а продав за 8 грн. потім знову купив за 9 грн, а продав за 10 грн. Який прибуток він одержав?   ( 2 грн.)
3. Обчислити  501²- 499²   (2000)
4. Відновіть запис числа  82**, якщо відомо, що воно ділиться на 90.   ( 8280)
5. У пасажирському літаку 108 місць. На кожних двох пасажирів, які сидять на своїх місцях припадає одне порожнє місце. Скільки пасажирів у літаку?   (72)

Додаткові завдання.

1. На столі стоять 16 склянок. Із них 15 стоять правильно, а одна – перевернута догори денцем. Дозволяється одночасно перевертати будь-які чотири склянки, чи можна, повторюючи цю операцію кілька разів, поставити                    всі склянки правильно?  (Ні, тому, що кількість перевернутих і не перевернутих склянок завжди буде непарною)
2. У трикутнику АВС кути дорівнюють  48°, 58°, 64°. Чи може периметр цього трикутника дорівнювати 10 см?  (Такого трикутника не існує)
3. Собака погнався за лисицею, коли та була на відстані 120 м від нього. Скільки часу знадобиться собаці, щоб догнати лисицю, якщо лисиця пробігає за хвилину 320 м, а собака -  350?   ( 4 хв.)
4. Кожне з трьох натуральних чисел поділили на їх суму і додали одержані           числа. Яке число дістали?   (1)

Підведення підсумків. Визначається команда переможець і нагороджується грамотою.