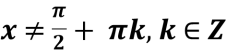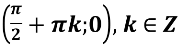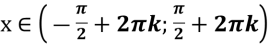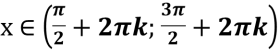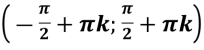МАТЕМАТИЧНЕ ДОМІНО "Властивості тригонометричних функцій"

МАТЕМАТИЧНЕ ДОМІНО

Тема: «Властивості тригонометричних функцій»

Мета: повторити властивості тригонометричних функцій в ігровій формі.

Спосіб використання: роздрукувати матеріал, розрізати на картки, гру розпочинає той учень у кого картка з пустою клітинкою зліва, а закінчує той у кого картка з пустою клітинкою з права.

Тригонометричні функції

y=sin X ; y=cos X ;

y= tg X ; y=ctg X

Область визначення - R

y=sin X ; y=cos X

Область значень – R

y=tg X ; y=ctg X

D(f)

y= tg X

E(f) = [-1; 1]

y=sin X ; y=cos X

Функція непарна

y=sin X; y= tg X ;

 y=ctg X

Графік функції симетричний осі ОУ

y=cos X

Графік функції перетинає вісь ОУ у точці (0;0)

y=sin X; y= tg X

Графік функції перетинає вісь ОУ у точці (0;1)

y=cos X

Графік функції перетинає вісь ОХ – у точках (πk; 0), де k Z

y=sin X; y= tg X

Графік функції перетинає вісь ОХ–у точках

y=cos X; y=ctg X

Функція y=sinX додатна на проміжку:

,

Функція y=sinX від’ємна  на проміжку:

,

Функція y=cosX додатна  на проміжку:

,

Функція y=cosX від’ємна  на проміжку:

,

Функція зростає на проміжках

,

y= tg X

Функція спадає на проміжках

,

y=ctg X

Функція максимальна у точках     ,

y=sinX

Функція мінімальна у точках

,

y=cosX

Найбільших і найменших значень функція не має

y= tg X ; y=ctg X