Математичний гурток Відповіді
Генерал і чоботи
Підрахунки граней зробимо по іншому. 20 крб, що залишилися у генерала, 3 крб привласнив солдат і по 1 крб вернуті інвалідам. Разом 25 крб. В умові свідомо допущено помилку, по підрахунку грошей. Додавши по 11,5 крб, ми отримали 23 крб, яких в наявності немає.
Справді, гроші інвалідів, які ми додаємо, можуть змінюватися. Якби солдат привласнив собі 4 крб, а інвалідам вернув по 0,5 крб, то вони заплатили б по 12 крб, разом 24 крб і 4 крб у солдата. Маємо суму 28 крб. тут зайвих 3 крб.
«Довести, що трикутник рівнобедрений, якщо в ньому дві бісектриси рівні». Пізніше задача була розв’язана і кількома способами. В математичній літературі задача зустрічається як теорема «Штейнера-Лемуса» швейцарського і французького математиків.
Покажемо один із способів розв’язання цієї задачі.
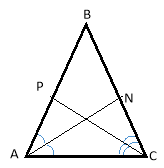
АN i CР – бісектриси кутів А і С ∆АВС.
АN = CР. Відомо, що бісектриси в трикутнику виражаються формулами
![]() i
i ![]() , де р – півпериметр; а, b і с - сторони трикутника.
, де р – півпериметр; а, b і с - сторони трикутника. ![]() . Маємо
. Маємо ![]()
aбо ![]()
![]() .
.
Замінивши р дробом і зробивши відповідні перетворення одержимо рівність ![]() .
.
Вирази перемножимо, перенесемо в одну частину і розкладемо на множники, одержимо: ![]() .
.
Звідси с-а=0, с=а. ∆АВС – рівнобедрений.
Відповіді до задач
- Рибка і кулька.
- а)
|
|
1 |
7 |
2 |
9 |
1 |
7 |
2 |
: |
1 |
9 |
= |
9 |
1 |
0 |
0 |
9 |
|
|
1 |
7 |
1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
9 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
9 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
7 |
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
7 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
б)
|
|
6 |
3 |
1 |
9 |
3 |
8 |
6 |
2 |
5 |
|
|
|
|
|
|
|
6 |
2 |
5 |
|
|
|
1 |
0 |
1 |
1, |
1 |
0 |
0 |
8 |
|
|
|
|
6 |
9 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
3 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
в)
|
|
= |
4 |
1 |
2 |
1 |
2 |
||||||||||
|
|
1 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
7 |
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
6 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
8 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
2 |
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
6 |
4 |
8 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
6 |
4 |
8 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
4. 1, 3, 9 і 27 кг.
5.
1) сідають два розбійники. Один розбійник залишається, другий вертає човен.
2) сідають два розбійники, один залишається, інший вертає човен.
3) сідають два солдати. Човен вертають розбійник і солдат.
4) сідають два солдати. Човен вертає розбійник.
5) сідають два розбійники. Всі без жертв переправились на інший беріг річки.
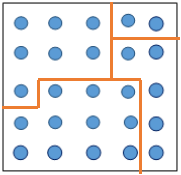 6.
6.
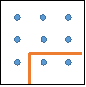
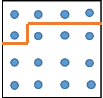
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7.
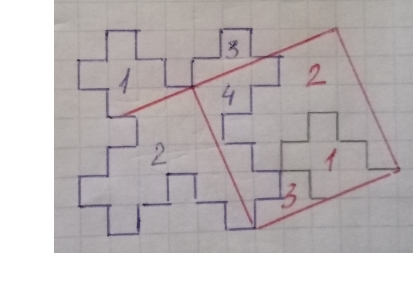
8.
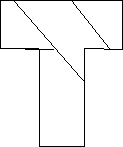 9.
9.
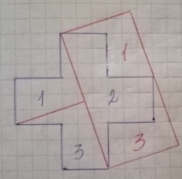
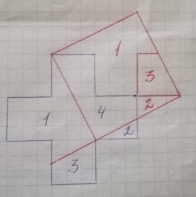 10. а) б)
10. а) б)
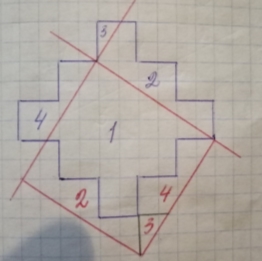 11.
11.
13.
а) 1) Розкладемо монети на три купки по 9-ть монет у кожній. Зважуємо будь-які 2-і купки. Визначаємо купку з фальшивою монетою.
2) розбиваємо монети на три купки. В кожній по три монети. Аналогічно зважуємо і визначаємо купку з фальшивою монетою.
3) нарешті зважуємо будь-які дві монети. Фальшиву монету визначити легко.
б)Пронумеруємо монети від 1 до 12. Розібємо монети на 3 купи по 4-и монети.
Можливі випадки:
Якщо І.
1) 1, 2, 3, 4=5,6,7,8, то фальшива монета серед монет 9, 10, 11, 12 - справжні
2) 1,2, 3=9, 10,11; 3) 1>12, монета 12 фальшива і легша.
3) 1<12, монета 12 фальшива і важча.
2) 1,2, 3>9, 10,11; 3) 9=10, монета 11 фальшива і легша.
3) 9<10, монета 9 фальшива і легша.
3) 9>10, монета 10 фальшива і легша
2) 1,2, 3<9, 10,11. (Міркування аналогічні).
Якщо ІІ
- 1, 2, 3, 4>5,6,7,8, тоді монети 9, 10, 11, 12 – справжні.
- 1, 2, 3, 8=9, 10, 11, 4, тоді фальшива монета серед монет 5, 6, 7.
3) 5=6, монета 7 фальшива і легша.
3) 5<6, монета 5 фальшива і легша.
3) 5>6, монета 6 фальшива і легша
2) 1, 2, 3, 8>9, 10,11,4, тоді фальшива монета серед монет 1, 2, 3
3) 1=2, монета 3 фальшива і важча.
3) 1<2, монета 2 фальшива і важча.
3) 1>2, монета 1 фальшива і важча
2) 1, 2, 3, 8<9, 10,11,4, тоді фальшива монета серед монет 4 і 8
3) 1=4, монета 8 фальшива і важча.
3) 1<4, монета 4 фальшива і важча.
3) 1>4, монета 4 фальшива і важча
в) Пронумеруємо мішки. 3 1-го мішка візьмемо 1 монету, з 2-го – 2-і, з 3-го – 3 монети і т.д.
Всього буде 55 монет. Якби всі монети були справжні, то вони мали б масу 550 г. Якщо маса буде 549 г., то фальшиві монети у 1-му мішку, якщо 548 г., то в 2-му і т.д.
21. Будуємо точку М1 симетричну М відносно прямої а. Пряма М1N перетне пряму а у точці Р. Точка Р – шукана.
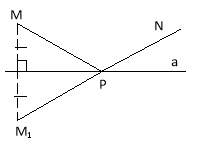
 22.
22.
Проведемо пряму NK ![]() а. Відкладемо відрізок NK, який дорівнює відстані між прямими а і b. Пряма МК перетинає пряму а у точці А. Відрізок АВ
а. Відкладемо відрізок NK, який дорівнює відстані між прямими а і b. Пряма МК перетинає пряму а у точці А. Відрізок АВ![]() а є шуканим.
а є шуканим.
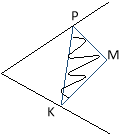
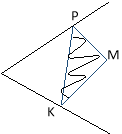
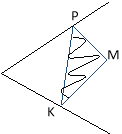 23. Будуємо точки М1 та М2 симетричні точці М відносно сторін кута.
23. Будуємо точки М1 та М2 симетричні точці М відносно сторін кута.
Пряма М1М2 перетинає сторони кута в точках К і Р. Трикутник МРК має найменший периметр.
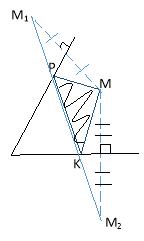
24.
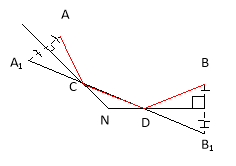
Будуємо точки А1 і В1 симетричні сторонам кута. Пряма А1В1 перетне сторони кута в шуканих точках С і D.
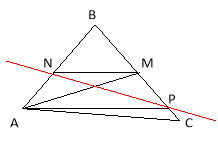 25. Точка Р – довільна, АМ – медіана
25. Точка Р – довільна, АМ – медіана ![]() . Проведемо MN||AP. Пряма NP – шукана.
. Проведемо MN||AP. Пряма NP – шукана.
27.
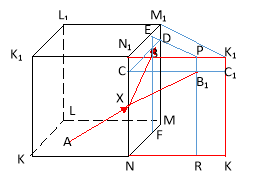 В грані NN1M1M через точку В проведемо CD||NM1 i EF||MM1. Грань NN1M1M повернемо на 90°. Вона лежатиме в площині передньої грані куба. Проведемо EP||M1K1, CC1||N1K1 i PR||NN1. Одержимо точку В1. Відрізок АВ1 перетне ребро NN1 в шуканій точці Х.
В грані NN1M1M через точку В проведемо CD||NM1 i EF||MM1. Грань NN1M1M повернемо на 90°. Вона лежатиме в площині передньої грані куба. Проведемо EP||M1K1, CC1||N1K1 i PR||NN1. Одержимо точку В1. Відрізок АВ1 перетне ребро NN1 в шуканій точці Х.
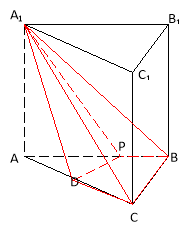
28. Можна
АВСА1В1С1 – пряма трикутна призма.


про публікацію авторської розробки
Додати розробку
