Математичний гурток, завдання

«Все тече, все змінюється» - говорив Геракліт, тому й освіта, зокрема математика постійно реформується.

 Школа не стоїть осторонь проблем і викликів, які сьогодні ставить перед нею сучасне життя. Учителі повинні «вирощувати» молодь, яка не тільки адаптується до сучасного ритму життя, а й буде конкурентно спроможною на ринку праці.

Математика створює широкі можливості для всебічного розвитку особи. Вона вчить логічному мисленню, вчить встановлювати причинно-наслідкові зв’язки, вчить обґрунтовувати їх. Математичне мислення ми свідомо «переносимо» й використовуємо у різних галуззях життя. Цьому дітей треба вчити.

Позакласна, зокрема гурткова, робота зорієнтована на досягнення обов’язкового рівня математичної підготовки. Невимушена форма спілкування глибше розкриває учня, підвищує його інтерес до математики.

Залучати дітей до гурткової роботи потрібно ще з молодшого віку. Вони його відвідують добровільно. Гурток є особливою формою співпраці учителя й учня.

Програма математичного гуртка зорієнтована на вік дітей. Роботу слід наповнювати цікавими, нестандартними задачами, розв’язування яких не обов’язково повинно опиратися на знання математики. Таких задач існує навколо нас досить багато. На уроках їх не розв’язують, а дають для домашнього опрацювання.

Такі завдання сприймаються з цікавістю, спонукають до роздумів, нестандартного мислення, розвивають уяву, на інтуїтивному рівні вгадується відповідь, а потім доводимо її істинність.

Перед тим, як запропонувати завдання, пригадаємо історії появи деяких з них. Траплялись різні ситуації в яких під час розмови, спілкування пропонувалися цікаві задачі, які інтригували і не покидали свідомість доти, поки не були розв’язані.

Ще навчаючись в інституті, моя група жила цікавим життям. У нас появлялись задачі запропоновані друзями або викладачами. Хто першим їх розв’язував, отримував винагороду - відро квасу. Ось перші дві з них за які я отримав винагороду.

Задача1.

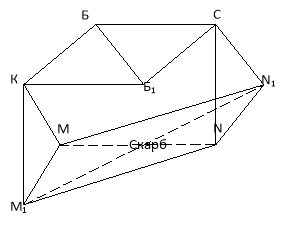
Було знайдено записку в якій було сказано: якщо йти від берези (Б) до калини (К), а потім під прямим кутом пройти ще таку відстань, то одержимо точку М, а якщо йти від берези до сосни, а потім знову під прямим кутом пройти таку саму відстань, то одержимо точку N. Середина між М і N є точка, в якій заховано скарб. Але коли прийшли на вказане місце, то берези вже не було. Залишились тільки камінь і сосна. Як знайти скарб?

Доведемо, що де б не росла береза, скарб буде знаходитись в одній і тій же точці.

Доведення

За умовою КБ=КМ і КБ КМ, СБ=СN і СБ СN. Оскільки берези на вказаному місці не було, то візьмемо довільну точку Б₁ і виконаємо аналогічні побудови. Одержимо точки М₁ і N₁. При повороті на 90◦ за рухом стрілки годинника навколо точки К  ∆КББ₁ перейде у ∆КММ₁, тому ББ₁=ММ₁ і ББ₁ ММ₁.

 

∆СББ₁ перейде у ∆СNN₁ при повороті навколо точки С на кут 90◦ градусів проти руху годинникової стрілки, тому ББ₁=NN₁ і ББ₁NN₁. Виходить у чотирикутнику ММ₁NN₁: MM₁=NN₁ і MM₁||NN₁, тому це паралелограм, MN і M₁N₁ його діагоналі, які перетинаються в точці К, в точці , де захований скарб.

Задача 2.

Чи ділиться число на 641 без остачі?

Розв’язання

Розв’язок подано у вигляді, який записав ще 45 років тому.

641=5;

.

Якщо , той дане число кратне 641.

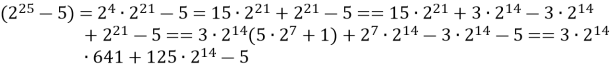
Якщо , то дане число кратне 641.

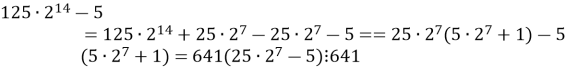
Відповідь: так.

Ці завдання одні з перших були записані у загальний зошит. Їх кількість збільшувалась, вона збільшується і по сьогодні. Цікаві задачі зустрілись в газетах і журналах (не тільки математичного профілю). Один із співрозмовників, з яким я у електропоїзді їхав до Києва запропонував таку задачу: «В центрі круглого озера плаває людина. По периметру озера бігає людоїд, швидкість якого у 4 рази більша швидкості плавця. Чи може врятуватися людина, якщо вибравшись з озера на мить раніше, ніж тут появиться людоїд, швидкість її набагато більша швидкості людоїда?»

Через півгодини ще у поїзді він отримав розв’язок.

 

 

 

 

 

 

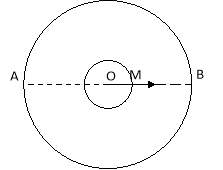
Нехай людоїд перебував у точці А, а людина у центрі озера, радіус якого 10 м.

Якщо плавець рухатиметься у напрямі точки В і пропливе 10 м, людоїд за цей час  пробіжить 40 м, проте довжина півкола дорівнює  м. тому людоїд вже чекатиме на плавця.

Плавець вибирає таку стратегію. Рухаючись у колі радіусом

 м, він завжди може вибрати таке положення (точка М), щоб розміщуватись з людоїдом на одній прямій АО, оскільки кутова швидкість людини більша за кутову швидкість людоїда. Плавець стартує з точки М у напрямі точки В. Відстань МВ = 7,5 м. Людоїд за цей час пробіжить м. але 30<31,4, тому людина врятуватись може.

Іншу задачу я почув на автовокзалі, коли чекав рейсовий автобус.

У генерала були чоботи. Він запропонував солдатові, щоб той їх продав на базарі. На базарі вони  не були продані. Повертаючись назад солдат на містку зустрів двох інвалідів. В одного не було лівої ноги, а іншого правої. Солдат пропонує їм чоботи. Вони погодились купити. Кожен з них заплатив по 12,5 крб. Разом 25 крб. Коли гроші солдат приніс генералу, той сказав, що він дорого їх продав. Віддає солдату 5 крб і просить, щоб він їх повернув інвалідам. Солдат привласнив собі 3 крб, а інвалідам вернув по 1 крб. Виходить вони заплатили по 11,5 крб. Разом 23 крб і 3 крб у солдата. Маємо 26 крб. Де взявся 1 крб? Поміркуйте.

Пам’ятаю, одну з задач, яку тоді в студентські роки не зміг розв’язати.

 «Довести, що трикутник рівнобедрений, якщо в ньому  дві бісектриси рівні». Пізніше задача була розв’язана і кількома способами. В математичній літературі задача зустрічається як теорема «Штейнера-Лемуса» швейцарського і французького математиків.

Подібних прикладів можна навести досить багато.

А зараз я пропоную невеликий відсоток задач для різних за віком учнів та різним рівнем знань.

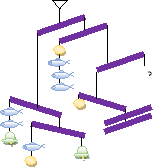
Задача 1. Рівновага

Д. Бернард, видатний англійський математик, назвав цю систему «еквілябр». «Еквілябр» висів у нього в кабінеті, поки якийсь неврівноважений суб’єкт не вкрав два предмети, які врівноважували систему.

Які це були предмети, якщо нічого іншого, крім того, що зображено на малюнку – рибки, кульки, коромисла і дзвіночка --  там не було. Вагою нитки можна знехтувати, а вагою коромисла – ні.

Задача 2.

В рівності замість кожної букви поставити цифру. Різним буквам відповідають різні цифри. Перед комою у правій частині рівності стоїть нуль. Відновіть запис.

Задача 3.

Замініть зірочки цифрами:

а)

1

*

*

*

1

*

*

:

1

*

=

*

1

*

*

*

*

*

1

1

*

*

*

1

*

*

*

*

1

1

б)

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*,

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

0

в)

=

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

0

Задача 4.

Їхав дід на базар і віз гирю 40 кг. По дорозі гиря впала і розбилася на такі 4-и частини, якими можна зважити від 1 до 40 кг включно. Які це частини?

 

Задача 5.

До берега річки підійшли три розбійники і три солдати. Усім їм треба переправитися на інший берег. Біля берега  є човен, у який можуть сісти максимум дві людини. Якщо в який момент часу на одному березі річки розбійників більше, ніж солдат, розбійники вбивають солдат. Якщо їх порівно або менше від солдат, жертв немає. Як усім без жертв переправитись на протилежний берег річки?

 

 

 

 

 

Задача 6. Задача тесляра.

У тесляра було дві квадратні дошки. Сторона однієї 60 см, а другої 80 см. Кожну з двох даних дощок слід розрізати, не зачепивши отворів, (підказка на дві частини) так, щоб склеїти квадратну дошку з стороною 10 см. Тесляр цю задачу розв’язав.

 

 

 

 

Задача 7.

 

У прямокутнику розмірами 8х9 клітинок зображено вісім світлих фігур. Попробуйте скласти з цих фігур квадрат, вирізавши їх.

1
			4			5
		2				6
				7
	3
						8

 

 

 

 

 

 

 

 

Задача 8

Розрізати дану фігуру на 4 частини, з яких можна скласти квадрат.

 

 

 

 

 

 

Задача 9.

З 4-х частин скласти букву «Т»

 

 

 

 

 

 

 

 

 

 

 

 

Задача 10. Розрізати хрест: а) на 4-и частини, з яких можна скласти квадрат.

б) на 3-и частини, з яких можна скласти прямокутник довжина якого у 2 рази більша за ширину.

 

 

       Задача 11.

Розрізати фігуру двома прямими так, щоб можна було скласти квадрат.

 

 

 

 

 

Задача 12. Американська головоломка.

Маємо чотири розгортки куба, грані якого пофарбовані у 4-и кольори: зелений (з), червоний (ч), синій (с), жовтий (ж).

 

 

 

Ці кубики треба укласти так, щоб на кожній великій грані утвореного паралелепіпеда були 4-и різні кольори.

 

 

 

 

 

 

Задача 13. Магічний квадрат.

Магічний квадрат - це така таблиця, в якій сума цифр

по діагоналях, горизонталях і вертикалях є однаковою. Таблицю, як правило, заповнюють числами від 1 до 9; 1 до 16; 1 до 25…

8	1	6
3	5	7
4	9	2

Найменший магічний квадрат 3-го порядку може мати вигляд.Сума цифр 15.

 

Алгебраїчна модель магічного квадрата 3х3

a+b+2c	a	a+2b+c
a+2b	a+b+c	a+2c
a+c	a+2b+2c	a+b

 

 

 

 

67	1	43
13	37	61
31	73	7

Англійський математик Дьюдені Генрі Ернест (10.4.1857-24.4.1930) творець і популяризатор головоломок склав магічний квадрат 3х3 з простих чисел. (Лише 1 не є простим)

 

Чим більший квадрат, тим складніше його заповнювати. Наприклад, квадрат 8-го порядку  може мати вигляд. Сума його чисел 260.

 

64	2	3	61	60	6	7	57
9	55	54	12	13	51	50	16
17	47	46	20	21	43	42	24
40	26	27	37	36	30	31	33
32	34	35	29	28	38	39	25
41	23	22	44	45	19	18	48
49	15	14	52	53	11	10	56
8	58	59	5	4	62	63	1

 

 

 

 

 

 

 

 

 

Задача 14. Задачі на зважування.

а) З 27 монет одна фальшива. Вона легша за справжню. Як за допомогою трьох зважувань, на терезах без гирьок, знайти фальшиву монету.

б) З 12 монет одна фальшива, проте невідомо, важча вона чи легша від справжніх. За три зважування на терезах без гирь треба відшукати фальшиву монету і визначити, легша вона чи важча  за справжню.

в) Є 10 мішків з монетами різної кількості однакового номіналу.В одному мішку всі монети фальшиві. Нехай справжня монета має масу 10 г, а фальшива 9г. Як за допомогою лише одного зважування відшукати мішок з фальшивими монетами, якщо в наявності є вага і різний набір гир?

Задача 15. Математичні несподіванки

153=1³+5³+3³

370=3³+7³+0³

371=3³+7³+1³

407=4³+0³+7³

1634=1⁴+6⁴+3⁴+4⁴

8208=8⁴+2⁴+0⁴+8⁴

9474=9⁴+4⁴+7⁴+4⁴

4150=4⁵+1⁵+5⁵+0⁵

4151=4⁵+1⁵+5⁵+1⁵

54748=5⁵+4⁵+7⁵+4⁵+8⁵

675+824=(6³+7³+5³)+(8³+7³+2³)

672+875=(6³+7³+2³)+(8³+7³+5³)

;; ;

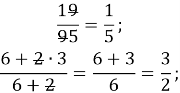
9∙9=81

99∙99=9801

999∙999=998001

9999∙9999=9998001

------------------------------------------

---------------------------------------

 

 

 

Задача 16

100895598169=898423∙112303 – праворуч стоять прості числа (П. Ферма)

Задача 17

Формула Ейлера при значеннях  х=0; 1; 2; …; 39 дає прості числа. З перших 2398 чисел, які дає ця формула, рівно половина прості.

При вивчені теми «Прямокутний трикутник» (7кл) розв’язуємо базову задачу. «Довести, що медіана у прямокутному трикутнику, проведена до гіпотенузи, дорівнює половинні гіпотенузи». Після цього даю гуртківцям задачу.

Задача 18.

На вертикальну стіну сперта драбина. Піднімаючись по ній, ноги дійшли до її середини (т. М) і драбина плавно почала сповзати по стіні, поки повністю не лягла на горизонтальну поверхню. По якій лінії рухались ноги: відрізку, ламаній, криві і т.д.?

 

 

 

 

Після того, як у математиці починаємо використовувати  систему координат, видозмінюємо цю задачу.

Задача 19.

Відрізок, заданої довжини,  своїми кінцями ковзає по координатних осях. Яку геометричну фігуру описує точка, яка є серединою відрізка?

Легко встановити, що такою фігурою є коло з центром у початку відліку і радіусом, який дорівнює половині відрізка.

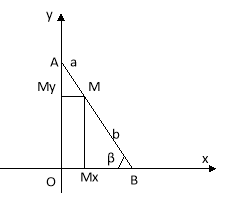На гуртку розглядаємо задачу ,коли точка М не є серединою.

Нехай точка М ділить відрізок на частини АМ=а і ВМ=b, aВ=β.

З ∆ММ_хВ (М_х=90°) ММ_х=у=bsinβ.

З ∆АММ_у (М_у=90°, М=β)

ММ_у=х=аcosβ.

;     

Бачимо, що точка М рухається по лінії, яка описується рівнянням
 

Це є канонічне рівняння еліпса. Потім даємо означення еліпса і виводимо його рівняння.

А якщо точка М не лежить на відрізку, а на прямій АВ, то яку лінію вона описує?

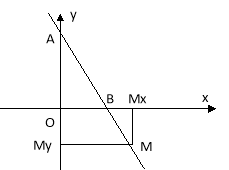Нехай АМ=а, ВМ=b, aОВА=β.

З ∆МВМ_х (В=β, М_х=90°)

ММ_х=у=bsinβ.

З ∆АММ_у (М_у=90°) ММ_у=х=аcosβ.

 

 

Виконавши аналогічні перетворення, одержимо рівність
 

І в цьому випадку точка М описує еліпс.

Якщо відрізок АВ своїми кінцями буде ковзати по координатних осях з 1-ї по 4-ту чверті, то кут β буде змінюватись від 0 до 2π, і тоді еліпс буде замкненою кривою.

Після вивчили тему «Перерізи многогранників» 10 клас доцільно на гуртку розглянути перерізи тіл обертання, зокрема конуса.

Але спочатку розв’язуємо задачу: «В кут S вписали два кола, які між собою дотикаються. Проведемо пряму АD, яка є їх спільною дотичною. Довести, що AF₁=F₂D.

 

 

Доведення

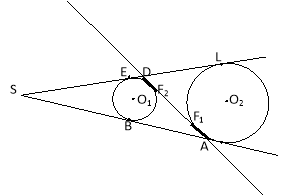SL=SK;

SK=SB+BA+AK (1)

SL=SE+FD+DL (2), але AK=AF₁, а ED=DF₂і DL=DF₁, як дотичні проведені до кола з однієї точки.

Також SB=SE,тому з рівності (1) і (2) маємо:

BA+AF₁=F₂D+DF₁ (3).

AB=AF₂=AF₁+F₁C, DF₁=DF₂+F₂A

Виконаємо підстановку у рівність (3).

AF₁+F₁F₂+AF₁=F₂D+DF₂+F₂F₁

2AF₁=2F₂D

AF₁=F₂D.

Звідси легко встановлюємо, що ЕL=ВК=AD.

Задача 20.

Якщо площина перетинає прямий круговий конус і утворює з віссю конуса кут α (,то в перерізі отримаємо еліпс.

Доведення

Проведемо січну площину. У конус впишемо дві кулі, які дотикаються конуса і січної площини з різних боків відповідно в точках F₁і F₂Лінії, по яких дотикаються кулі з бічною поверхнею конуса, є кола з центрами.

 

Ці кола лежать у паралельних площинах, тобто є гомотетичними з центром гомотетії у точці S. Нехай довільна твірна перетинає кола відповідно в точках Q i P, а січну площину у точці М. При гомотетії точки кола з центром переходять у відповідні точки кола з центром, тому EM=QP=BK. Виконаємо осьовий переріз конуса. Одержимо рисунок попередньої задачі, в якій було доведено, що ЕL=ВК=AD, тому QP=AD. Проведемо  відрізки MF₁ i MF₂. MQ=MF₂ оскільки це дотичні проведені з точки М до кулі з центром О₁. Аналогічно MF₁=MP.

Нарешті QP=MQ+MP=MF₁+MF_2.

Гуртківцям подобаються нестандартні задачі на максимум і мінімум. Ось деякі з них

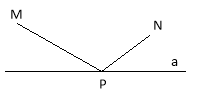Задача 21. Дано пряму а і дві точки M i N, які лежать в одній півплощині. На прямій а знайти таку точку Р, щоб сума МР+РN була мінімальною.

 

 

 

Задача 22. Прямі a i b паралельні. Дано точки M i N ( див. рис.) АВ. В якому місці треба побудувати відрізок АВ, щоб сума МА+АВ+BN була мінімальною.

 

 

 

 

 

 

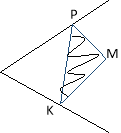
Задача 23. Довільна точка М розміщена в середині кута. На сторонах кута знайти такі точки Р і К, щоб Р_∆МРКбув мінімальним.

 

 

 

 

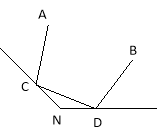Задача 24.

Дано кут N і точки А і В (див. рис). На сторонах кута знайти такі точки С і D, щоб сума АC+СD+DB була мінімальною.

 

 

 

 

Задача 25. Через точку, яка лежить на стороні трикутника і не є його серединою, провести пряму, яка поділить трикутник на дві рівновеликі площі.

Розгляньте випадки, коли точка лежить за трикутником  або в середині нього.

Задача 26. Через точку, яка лежить в середині кута, провести пряму, яка відтинає трикутник: а) найменшої площі; б) найменшого периметра.

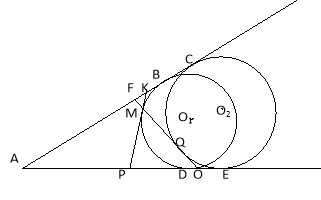Розглянемо випадок б).

Побудуємо коло з центром О₁, яке дотикається сторін кута в точках B i D і проходить через точку М. Проведемо дотичну КР, яка проходить через точку М.

Периметр  ∆АКРдорівнює 2АВ або дорівнює 2AD. (Довести самостійно).

Доведемо, що ∆АКР має найменший периметр. Через очка М проведемо інший відрізок FO. Одержимо ∆AFO. Побудуємо зовні вписане коло в цей трикутник з центром О_2, яке дотикається сторін кута в точках С і Е.

Р_∆AFO=2АС=2АЕ.  Оскільки  АС>АВ, то Р_∆AFO>Р_∆AКР, що й треба було довести.

Після вивчення теми «Ортогональне проектування» (10 кл) учням пропонуємо задачу: «Маємо куб, ребро якого 1 дм. Знайти площу найбільшої ортогональної проекції цього куба на площину».

Задача 27.

На передній грані непрозорого куба в точці А сидить павук.

На правій грані в точці В сидить муха. На ребрі куба треба знайти таку точку Х, щоб маршрут від павука до мухи А→Х→В був найкоротшим?

 

 

 

 

Задача 28.

Чи можна побудувати чотирикутну піраміду в якій тільки дві протилежні грані перпендикулярні до основи?

Задача 29

Записати будь-яке ціле число лише двійками.

Розв’язання

Для прикладу число , .

Справді,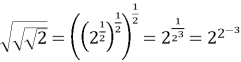

, .

Загальний розв’язок задачі такий:

а) якщо , то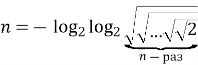

б) якщо , то .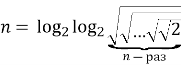

Відомо, що , тому будь-яке ціле число можна записати лише двійками за допомогою математичних символів і

 

Відомо, що довільний трикутник можна розв`язати, якщо відомі три його елементи (серед яких принаймні один повинен бути лінійний елемент).

Аргометр Бібікова розв`язує цю задачу за двома елементами, проте третім елементом виступає ширина лінійки.

Буває, треба швидко обчислити площу трикутника. І починається: вимірюємо всі його сторони  або дві сторони і кут між ними, або вимірюємо основу і висоту проведену до неї. Справа досить марудна . А чи немає такого відрізка, довжина якого чисельно дорівнювала б площі трикутника?

Виявляється, ще в 40-х роках минулого сторіччя російський математик Бібіков, сподіваючись прислужитись землемірам, винайшов простий прилад, який назвав аргометром. Пристрій цей якнайпростіший, бо складається із звичайної лінійки (із сантиметровими і міліметровими поділками) завширшки у 2 см.

 

 

 

 

 

 

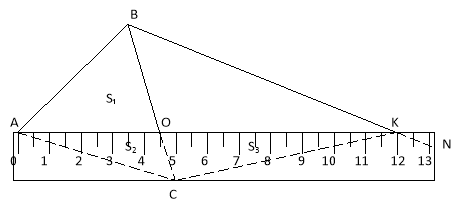
Нехай нам треба визначити площу ∆АВС. Для цього через вершину В проведемо пряму . Покладемо лінійку так, щоб початок відліку на лінійці збігався з точкою А, а точка С лежала на кромці другої сторони лінійки. Нехай пряма перетне лінійку у точці К. Довжина відрізка АК чисельно (у см²) дорівнює площі ∆АВС.

У побудові аргометра  використана ідея: трикутник, площу якого треба знайти, замінюють рівновеликим трикутником з висотою у 2 см.

Число операцій при цьому скорочується до двох: проведення паралельної прямої і вимірювання довжини відрізка АК.

Аргометром можна користуватися при визначенні площі довільного многокутника, розбивши його на трикутники.

Доведення:

; аналогічно .

З цих рівностей випливає, що

. Бачимо, що чисельно дорівнює довжині відрізка АК.

Як бачимо тут також присутній третій елемент, це ширина лінійки.

Переконаний, що такі різнопланові інтригуючі завдання підвищують інтерес наших учнів до «цариці наук» - математики.

Розв’язання запропонованих завдань будуть надруковані у наступних номерах журналу.