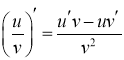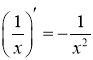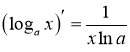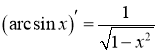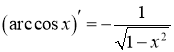Матеріали для повторення теми "Похідна" у процесі підготовки до ЗНО з математики
Поняття похідної. Таблиця похідних.
Приростом аргументу називається різниця між двома значеннями аргумента
![]() .
.
Приростом функції називається різниця між двома значеннями функції при різних значеннях аргумента
![]() .
.
Похідною функції ![]() в точці х0 називається границя відношення приросту цієї функції до приросту аргумента, коли приріст аргумента прямує до нуля.
в точці х0 називається границя відношення приросту цієї функції до приросту аргумента, коли приріст аргумента прямує до нуля.
![]()
![]()
![]() або
або ![]()
![]()
![]() .
.
Диференціюванням називається знаходження похідної або диференціала функції.
Основні правила диференціювання
|
1. |
|
2. |
|
3. |
|
4. |
|
Таблиця похідних
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
|
12. |
|
|
13. |
|
14. |
|
|
15. |
|
16. |
|
Похідна складної функції. Похідна функції, заданої
параметрично. Похідна оберненої функції.
Похідна функції, заданої неявно. Диференціал функції
Якщо 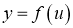 , a
, a 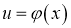 , то функція
, то функція  називається складною.
називається складною.
Похідна складної функції:
![]() .
.
Похідна функції, заданої параметрично, тобто у вигляді 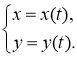 , обчислюється за формулою
, обчислюється за формулою
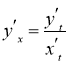
Якщо із співвідношення ![]() випливає співвідношення
випливає співвідношення ![]() , то функція
, то функція ![]() називається оберненою до
називається оберненою до ![]() .
.
Похідна оберненої функції
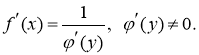
Якщо залежність між х і у виражена рівнянням, яке не можна розв’язати відносно у, або не можна розв’язати однозначно, то функція ![]() називається неявно заданою функцією.
називається неявно заданою функцією.
Неявно задані функції диференціюються як складні функції.
Диференціалом функції ![]() називається головна частина приросту функції, лінійна відносно приросту аргументу:
називається головна частина приросту функції, лінійна відносно приросту аргументу:
![]() .
.
Логарифмічне диференціювання. Рівняння дотичної та нормалі до графіка функції
Логарифмічною похідною функції ![]() називається похідна від логарифма цієї функції, тобто
називається похідна від логарифма цієї функції, тобто 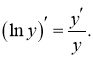
Застосування попереднього логарифмування часто спрощує обчислення.
Рівняння дотичної до графіка функції ![]() в точці М(х0; у0)
в точці М(х0; у0)
![]()
Рівняння нормалі до графіка функції ![]() в точці М(х0; у0)
в точці М(х0; у0)
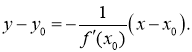


про публікацію авторської розробки
Додати розробку