Матеріали щодо організації самостійної діяльності учнів на уроках геометрії для 10-го класу до теми "Відстані і кути у просторі" (узагальнення понять)

Про матеріал

Виникнення інтересу до математики в учнів значною мірою залежить від методики її викладання. Потрібно турбуватися про те, щоб на уроці кожний учень працював активно, захоплено. І використовувати це як відправну точку для сприяння розвитку пізнавального інтересу. Велике значення для формування пізнавальних інтересів і потреб учнів має самостійна навчальна робота, яка є ніби каталізатором активних розумових і практичних їх дій. До того ж вона – засіб оцінювання і самооцінювання ефективності їхньої активної роботи.

Перегляд файлу

Тема уроку: Відстані і кути у просторі

(узагальнення понять)

Природа говорить мовою математики: літери цього мови - кола, трикутники та
інші математичні фігури.

Г. Галілей

Оціночна картка роботи на уроці учня

Мозкова атака

(0-4)

Математичний диктант (0-3)

Тестове опитування

(0-7)

Порожні комірки (0-4,5)

Задача (0-9,5)

Самостійна робота (0-7)

Мікрофон (0-5)

Всього (0-40)

Перевірка домашнього завдання

Зошити в кінці уроку викладач збирає на перевірку

Мотивація навчальної діяльності учнів

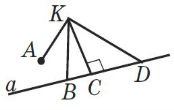
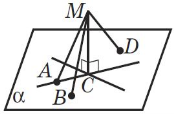
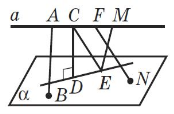
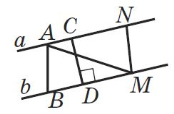
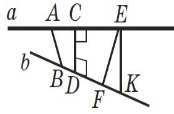
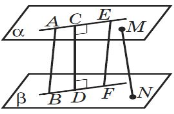
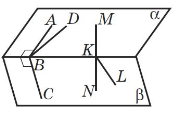
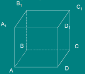
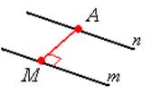
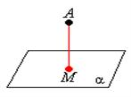
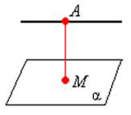
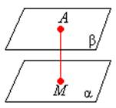
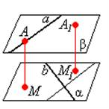
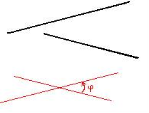
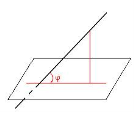
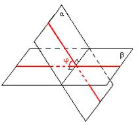
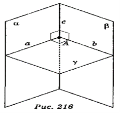
«Мозкова атака» Користуючись рисунками, дайте вiдповiдi на запитання. Сформулюйте вiдповiднi означення. (за кожну правильну повна відповідь 0,5 бали)

*Довжина якого з в*iдрiзкiв є вiдстанню
вiд точки K до прямої а?	вiд точки M до площини α?
вiд прямої a до площини α? (a\|\|α)	мiж прямими a i b? (a\|\|b)
мiж прямими a i b? (a і b мимобіжні)	мiж площинами α i β? (α\|\|β)
*Який iз кутiв є кутом мiж*
прямою AB i площиною α?	площинами α i β?

Узагальнення окремих фактів

Математичний диктант «Незакінчене речення». Закінчити речення (перевірка в парах, за кожну правильну відповідь по 0,3 бали)

Дві прямі називаються перпендикулярними, якщо ...
2) Пряма називається перпендикулярною до площини, якщо ...
3) Пряма перпендикулярна до площини, якщо вона ...
4) Якщо одна з двох паралельних прямих перпендикулярна до третьої прямої, то ...
5) Через дану точку простору можна провести пряму, перпендикулярну даній прямій, і притому ...
6) Всі прямі, які проходять через дану точку прямої і перпендикулярні до цієї прямої, лежать в ...
7) Якщо одна з двох паралельних прямих перпендикулярна площині, то ...
8) Дві прямі, перпендикулярні до однієї і тієї ж площини, ...
9) Якщо площина перпендикулярна до однієї з двох паралельних прямих, то ...
10) Якщо дві площини перпендикулярні до прямої, то вони ...

Тестове опитування. Оберіть одну правильну відповідь (за кожну правильну відповідь 0,5 бали)

1	На рисунку зображено куб. Визначте проекцію відрізка В₁D на площину АВС.
	а)	б)		в)	г)		д)
	АВ	Точка В		ВС	Точка D		ВD
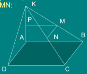
2	Точка К, яка лежить поза площиною квадрата АВСD, сполучена з вершинами квадрата. Через точку М відрізка КВ проведені прямі МР // АВ, MN // СВ. Тоді кут РМN
	а)	б)		в)	г)		д)
	Гострий	Розгорнутий		Прямий	Тупий		Визначити неможливо
3	Задано площину α і точку М. Скільки існує різних площин, які проходять через точку М і перпендикулярні до площини α?
	а)	б)		в)	г)		д)
	жодної	Тільки одна		безліч	Тільки три		Інша відповідь
4	Пряма а перпендикулярна до площини α, а площина α паралельна площині β. Яким є взаємне розташування прямої а і площини β?
	а)	б)		в)	г)		д)
	а//	а		а	а , але не перпендикулярна до неї		Визначити неможливо
5	Кутом між прямою і площиною називають кут між цією прямою і …
	А		Б			В
	її проекцією на площину		перпендикуляром, проведеним до площини			довільною прямою площини
6	Геометричним місцем точок простору, рівновіддалених від усіх точок даного кола, є …
	А		Б			В
	круг		площина			пряма
7	Скільки можна провести прямих, одночасно перпендикулярних до двох мимобіжних прямих?
	А		Б			В
	одну		жодної			безліч
8	Якщо точка М простору рівновіддалена від вершин прямокутника, то основою перпендикуляра, опущеного з точки М на площину прямокутника, є
	А		Б			В
	вершина прямокутника		центр кола, описаного навколо прямокутника			довільна точка площини
9	Кут β між двома площинами може бути …
	А		Б			В
	тупим		β = 0^º, β = 180^º			0^º ≤ β ≤ 180^º
10	Похилі, проведені з однієї точки простору, та їхні проекції на площину мають однакові довжини. Чи можуть похилі бути нахилені до площини під різними кутами?
	А		Б			В
	ні, ніколи		так, завжди			інколи таке можливо
11	Кутом між похилою і площиною називають кут між …
	А		Б			В
	похилою та перпендикуляром, проведеним з будь-якої точки похилої		похилою та її проекцією на дану площину			перпендикуляром, проведеним з будь-якої точки похилої та проекцією похилої
12	Кут β між прямою і площиною може бути …
	А		Б			В
	будь-який		гострий			0^º≤ β ≤ 90^º
13	У тетраедра бічні ребра рівні. Тоді …
	А		Б			В
	в основі тетраедра лежить рівнобедрений трикутник		бічні ребра утворюють однакові кути з площиною основи			основою тетраедра є прямокутний трикутник
14	Усі двогранні кути, утворені внаслідок перетину двох площин, рівні. Установіть взаємне розміщення цих площин.
	А		Б			В
	паралельні		перпендикулярні			співпадають

Повторення і узагальнення понять і засвоєння відповідної їм системи знань

1. Заповніть порожні комірки таблиці (за кожну правильну відповідь 0,5 бали)

*Відстані у просторі*	*Означення*
Між мимобіжними прямими	Довжина відрізка, який перпендикулярний до кожної з цих прямих і кінці якого лежать на цих прямих (довжина спільного перпендикуляра)
Від точки до площини
Від прямої до паралельної їй площини
	Відстань від будь-якої точки однієї площини до другої площини
*Кути у просторі*
Між двома прямими, що перетинаються
	Кут між прямими, які перетинаються і паралельні поданим прямим
	Кут між прямою і її проекцією на площину
Між площинами
	Фігура, утворена двома півплощинами зі спільною прямою, що їх обмежує
	Кут між двома прямими, які лежать у цих площинах і перпендикулярні до прямої перетину площин

2.Колективне розв’язування

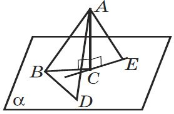
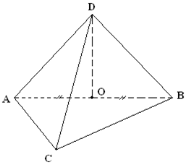Задача.

Дано: ΔАВС - рівносторонній,
О - середина АВ, ОD (АВС). АВ = 6см, ОD=3см. Знайти:
1) пари перпендикулярних прямих; (4х0,5 бали)
2) пари перпендикулярних прямої і площини; (3х0,5 бали)
3) пари перпендикулярних площин; (3х0,5 бали)
4) кути між DA, DB, DC та площиною ABC; (3х0,5 бали)
5) відстані від т. D до площини (АВС), від С до (DАВ), від А до (DОС); (3х0,5 бали)
6) відстані від точки D до прямих АВ, ВС, АС. (3х0,5 бали)

Самостійна робота

№	*І варіант*				*ІІ варіант*				*Бали*
1	Виконай рисунок. Через сторону AD прямокутника ABCD проведено площину α. BO - перпендикуляр до площини α. Назвiть кут мiж прямою BD i площиною α.				Виконай рисунок. Через сторону AD прямокутника ABCD проведено площину α. CO - перпендикуляр до площини α. Назвiть кут мiж прямою CA i площиною α.				2
	А	Б	В	Г	А	Б	В	Г
	∠BDA	∠ADC	∠ODB	∠BOD	∠CAO	∠CAB	∠ACO	∠DAO
2	Точка O - центр квадрата, MO - перпендикуляр до його площини. Знайдiть вiдстань вiд точки M до сторiн квадрата, якщо його площа дорiвнює 36 см², а MO= 4 см.				MO - перпендикуляр до площини квадрата, у якому O - точка перетину дiагоналей, MO= 3 см. Знайдiть вiдстань вiд точки M до сторiн квадрата, якщо його периметр дорiвнює 32 см.				2
	А	Б	В	Г	А	Б	В	Г
	210 см	5 см	32 см	4 см	53 см	3 см	5 см	8 см
3	Кут між площинами α і β - 60°. Точка А, яка лежить у площині α, віддалена від площини β на 12 см. Знайдіть відстань від проекції точки А на площину β до лінії перетину площин.				Кут між площинами α і β - 30°. Точка А, яка лежить у площині α, віддалена від лінії перетину площин на 12 см. Знайдіть відстань від точки А до площини β.				3

Підведення підсумків уроку

Прийом «Мікрофон» Вказати назву відстані, кута в просторі (за кожну правильну відповідь 0,5 бали)

Рефлексія

На уроці я

• узагальнив …

• удосконалив …

• найбільші труднощі відчував…

Оцінювання навчальних досягнень учнів

Таблиця переводу отриманих балів

*Набрані бали*	*40-38*	*37-35*	*34-31*	*30-27*	*26-23*	*22-18*	*17-13*	*12-9*
*Оцінка*	11	10	9	8	7	6	5	4

Описание: 3d-model-domika

Повідомлення домашнього завдання

Підготуватися до контрольної роботи:

- повторити матеріал за опорними конспектами

- розв’язати задачі

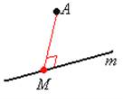
№1^о. Точка M знаходиться поза площиною α. MO - перпендикуляр, MA - похила до площини α. Знайдiть кут мiж прямою MA i площиною α, якщо MO = OA.

№2^*. Трикутник ABC — рівнобедрений прямокутний із прямим кутом C i гіпотенузою 4 см. Відрізок CM перпендикулярний до площини трикутника i дорівнює 2 см. Знайдіть відстань від точки M до прямої AB.

doc

Завантажити

Зберегти на потім

Додав(-ла)

Коваленко Світлана

Пов’язані теми

Геометрія, Матеріали до уроків

Додано

11 лютого 2018

Переглядів

1497

Оцінка розробки

Відгуки відсутні