Методична розробка практичного заняття "Обчислення визначенного інтегралу"
Міністерство освіти і науки України
Донецький національний університет економіки і торгівлі
імені Михайла Туган-Барановського
Краматорський технікум
Методична розробка
відкритого практичного заняття
Дисципліна: Вища математики
Тема заняття: «Обчислення визначеного інтегралу»
Спеціальність: 5.03051001 „Товарознавство та комерційна діяльність”
2017
Методична розробка практичного заняття з дисципліни «Вища математика». Підготувала викладач Краматорського технікуму Донецького національного університету економіки і торгівлі імені Михайла Туган-Барановського Кулешова Н.М.
5.11.2017р.
Викладено методику проведення практичного заняття із застосуванням методу проектів, що сприяє активізації уваги і мислення студентів, виховує відповідальність і навички колективної роботи з теми «Обчислення визначеного інтегралу».
Для викладачів вищої математики вищих навчальних закладів І-ІІ рівня акредитації.
Рецензенти:
Гуляєва Л.П. - викладач математики вищої категорії Краматорського технологічного технікуму.
Розглянуто і схвалено на засіданні циклової комісії загальноосвітніх та природничо-наукових дисциплін
Протокол № 4 від 12.11.2017р.
ЗМІСТ
Передмова…..…………………………………………………………………………….....4
1. Методика проведення практичного заняття за темою «Обчислення визначеного інтегралу»
- 1.1. План заняття………………………………………………...…………..…...…………5
- 1.2. Зміст проведення заняття..………...…………………………………….………...…..6
- 1.3. Методичне обґрунтування проведення заняття……………………………………...7
- 2. Література….…………………………………………………………………..……........9
3. Додатки
- Еталон виконання домашнього завдання ………………...…….…….…..……..10
- Картка самоконтролю ………..………..……….……..…………….……………..11
- Тест …………………………………..…………………..…………..……….…….12
- Таблиця-тест ……………………………………………...…………..…………....14
- Критерії оцінки тестів………………………………………….………………….16
- Інструкційна карта …………………………………...……………..……………...17
- Критерії оцінки знань студентів ……………………………..…………..............19
Передмова
Сучасні роботодавці зацікавлені в такому працівнику, що не тільки добре володіє необхідним теоретичним матеріалом, уміє застосувати отримані знання на практиці, але здатен сам «добувати» знання, орієнтуватися в нестандартній ситуації, а також може працювати в колективі.
Проведення практичного заняття з використанням методу проектів за темою «Обчислення визначеного інтегралу» дозволяю сформувати у студентів спеціальності «Товарознавство та комерційна діяльність» практичні уміння та навички щодо аналізу економічних показників господарської діяльності підприємств торгівлі.
Використання методу проектів сприяє активізації уваги і мислення студентів, виховує відповідальність і навички колективної роботи. Безперечною перевагою розв’язання задач в колективі , як і іншого методу активного навчання, є змушена активність студентів, що сприяє поліпшенню якості практичної підготовки, тобто більш ефективному досягненню кінцевої мети навчального процесу.
Головними факторами у виборі форм проведення практичних занять з дисципліни «Вища математика» при підготовці молодших фахівців зі спеціальності «Товарознавство та комерційна діяльність» є не тільки тема, мета, навчальний матеріал, але і рівень підготовленості студентів. Важливо показати студентам, що при рішенні економічних задач може бути застосовано математичний апарат. Іншими словами при вивченні різних тем вищої математики формувати у студентів уміння застосовувати математичне моделювання при рішенні економічних задач.
Мета методичної розробки показати методику проведення практичного заняття з теми «Обчислення визначеного інтегралу» з використанням методу проектів.
1. МЕТОДИКА ПРОВЕДЕННЯ ПРАКТИЧНОГО ЗАНЯТТЯ
- План заняття
Дисципліна: Вища математика.
Тема заняття: «Обчислення визначеного інтегралу».
Тип заняття: Формування практичних вмінь та навичок.
Вид заняття: практичне.
Форма проведення: з використанням методу проектів.
Група: ТК-16-А.
Дата проведення: 227.11.2017р.
Мета заняття:
методична: Удосконалити методику проведення практичного заняття з використанням методу проектів при викладанні вищої математики.
дидактична: Сформувати практичні навички застосування математичного апарату до розрахунку економічних показників.
виховна: Сприяти формуванню пізнавального інтересу, розвитку технічних вмінь застосовувати визначений інтеграл в практичній діяльності.
Методичне забезпечення заняття: Еталон виконання домашнього завдання(Додаток А), картка самоконтролю (Додаток Б), тест (Додаток В), таблиця – тест (Додаток Г), інструкційна карта (Додаток Е), Завдання щодо проведення самостійної роботи (Додаток Ж).
Технічні засоби навчання: персональний комп’ютер, документ-камера, мультимедійний проектор.
Міждисциплінарні зв'язки:
- Дисципліна: Математика
Тема: Застосування визначеного інтегралу,
- Дисципліна: Інформатика та комп’ютерна техніка .
Тема: Програма Power Point
- Дисципліна: Економіка підприємства
Тема: Товарні запасі підприємства; Нормалізація товарних запасів;
Прибуток підприємства.
- Дисципліна: Бухгалтерський облік.
Тема: Облік доходів та витрат.
Внутрідисциплінарні зв’язки:
Дисципліна: Вища математика
Тема: Невизначений інтеграл.
Тема: Диференціальні рівняння першого та другого порядку.
1.2. Зміст заняття
1. Організаційний момент :
- Привітання студентів
- Перевірка наявності студентів в аудиторії.
- Перевірка готовності студентів до проведення заняття.
- Повідомлення теми, навчальних цілей заняття:
Тема: «Обчислення визначеного інтегралу».
Метою проведення заняття є відпрацювання навичок знаходження визначеного інтегралу та формування вміння використовувати математичний апарат для розв’язання прикладних задач.
- Мотивація навчальної (пізнавальної) діяльності студентів.
Визначений інтеграл-фундаментальне поняття математичного аналізу, за допомогою якого досліджуються процеси і явища в природних, соціальних і економічних науках.
Однією із основних задач підприємств торгівлі є дослідження поведінки показників економічної діяльності. Використання визначеного інтегралу значно полегшує задачу дослідження.
- Підготовчий етап.
4.1. Перевірка домашнього завдання за допомогою документ-камери (додаток А) та відповіді на запитання, що виникли у студентів під час виконання домашнього завдання.
4.2. Актуалізація опорних знань (тестування) Додаток В,Г.
- Основний етап проведення заняття
Заняття проводиться з використанням інструкційної карти (додаток Е).
- Заключний етап:
6.1. Підведення підсумків заняття.
6.2. Оцінювання діяльності студентів на занятті.
7. Домашнє завдання
Методичне обґрунтування проведення заняття
Практичне заняття за темою «Обчислення визначеного інтегралу» проводиться зі студентами спеціальності «Товарознавство та комерційна діяльність».
Мета проведення заняття – сформувати практичні навички застосування математичного апарату до розрахунку економічних показників.
Заняття починається з організаційного моменту, який складається з привітання студентів та перевірка наявності студентів в аудиторії.
При проведенні мотивації звертається увага на те, що однією із основних задач підприємств торгівлі є дослідження поведінки показників економічної діяльності. Використання визначеного інтегралу значно полегшує задачу дослідження.
На підготовчому етапі проводиться актуалізація опорних знань. Даний етап складається з перевірки домашнього завдання, що було задано на попередньому занятті, перевірки теоретичних знань студентів за допомогою тесту (додаток В) та перевірки основних практичних навичок з використанням таблиць-тестів (Додаток Г). Домашнє завдання складається з двох частин: розв’язання визначених інтегралів та дослідницької роботи (створення власного проекту). Завдання виконується та оцінюється студентами самостійно. За допомогою документ-камери на дошці з’являється зразок домашнього завдання. За правильну відповідь студенти виставляють 1 бал в картку самоконтролю.
Перед виконанням практичних завдань студенти ознайомлюються з організацією його проведення. Безпосередньо практична робота виконується згідно з інструкційною картою (Додаток В). Практична робота складається із завдань, які розв’язуються індивідуально, колективно, та групами.
Дослідницька робота студентів реалізується через представлення власних проектів використання визначеного інтегралу в економічних задачах. В економіці користуються середніми величинами: обчислюють середню собівартість продукції, середню продуктивність праці. Проте, при вивченні деяких непостійних процесів в економці розраховуються величини зростання витрат виробництва, якщо збільшити обсяг продукції, і, навпаки, наскільки зменшаться витрати виробництва, якщо скоротити обсяг продукції; з’ясується залежність попиту на товар від ціни на нього. Середні величини відповіді на такі питання не дають, а тому варто застосувати визначений інтеграл в економічних розрахунках. Студенти демонструють результати творчої роботи-свої проекти, що стосуються використання визначеного інтегралу в розв’язанні задач економічного характеру.
Одним із завдань пропонується виконання студентами самостійної роботи (Додаток Ж), яка оцінується тільки викладачем.
Всі види робіт оцінюються як студентом так і викладачем.
Наприкінці підводяться підсумки і оцінюється робота студентів. Оцінки виставляються у відомість обліку роботи студентів за практичне заняття.
В журнал виставляється середній бал, що отримує студент за результатами роботи на занятті.
ЛІТЕРАТУРА
- Дубовик В.П., Юрик І.І. Вища математика: Навч. посібник. – К.: А.С.К., 2001.
- Овчинников П.П. та ін. Вища математика: Підручник. У 2 ч. – К.: Техніка, 2004.
- Шипачёв В.С. Высшая математика: Учебник для вузов. – М.: Высшая школа, 1998.
- Шкіль М.І., Колесник Т.В. Вища математика. У 3-х кн.. – К: Либідь, 2004.
- Вища математика: Збірник задач: Навч. посібник / За ред. В.П. Дубовика, І.І. Юрика. – К.: А.С.К., 2004.
- Шипачёв В.С. Задачник по высшей математике: Учебное пособие для вузов.- М.: Высшая школа, 2002.
- Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч.: Учебное пособие для вузов. – М.: Высшая школа, 2000.
Додаток А
Еталон виконання домашнього завдання
Приклад 1. Обчислити площу фігури, обмеженої:
1) синусоїдою ![]() і відрізком
і відрізком ![]() осі Ох;
осі Ох;
2) кубічною параболою у = х3, віссю Ох та прямими х = 2 і х = 5.
Розв’язання
1) 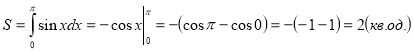
2) 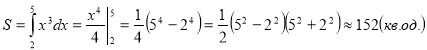 Відповідь: Sф = 152 кв.од.
Відповідь: Sф = 152 кв.од.
Приклад 2. Знайти площу фігури, обмеженої параболою у = 4 – х2 та прямими ![]()
![]()
Розв’язання
На відрізку [-2; 0] ![]()
а на відрізку [0; 2] ![]()
Шукану площу знаходимо як суму двох інтегралів:
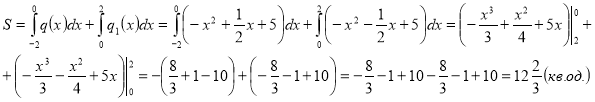
Також площу даної фігури можна обчислити раціонально, якщо звернути увагу на те, що фігура симетрична відносно осі Оу:
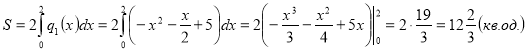
Відповідь: Sф = ![]() кв.од.
кв.од.
Приклад 3. Обчислити площу фігури, обмеженої кривими у = х2 і у = х3.
Розв’язання
![]() υ(х) = х3, а = 0, b = 1
υ(х) = х3, а = 0, b = 1
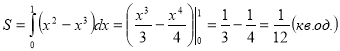 Відповідь: Sф =
Відповідь: Sф = ![]() кв.од.
кв.од.
Приклад 4. Обчислити площі плоских фігур, обмежену лініями ![]()
![]()
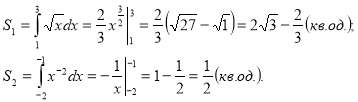 Відповідь: Sф =
Відповідь: Sф = ![]() кв.од.
кв.од.
Додаток Б
Картка самоконтролю
Прізвище, ім’я ___________________________________
Група___________________
|
1. |
Домашнє завдання (1б) |
|
|
2. |
Таблиця-тест (1б) |
|
|
3. |
Тест з теорії (1б) |
|
|
4. |
Усна робота (1б) |
|
|
5. |
Презентація (1б) |
|
|
|
Всього |
|
Додаток В
Тест
Дисципліна: Вища математика
Тема: Обчислення визначених інтегралів
1. Визначений інтеграл суми двох функцій 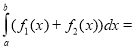
а) ![]() ; b)
; b) 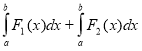 ;
;
c) 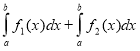 ; d) інша відповідь.
; d) інша відповідь.
2. Формула Ньютона-Лейбніца для обчислення визначеного інтеграла:
а) 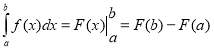 ;
;
b) 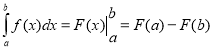 ;
;
c) 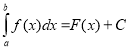 ; d) інша відповідь.
; d) інша відповідь.
3. Сукупність всіх первісних ![]() - це
- це
а) похідна функції ![]() ;
;
b) визначений інтеграл;
c) невизначений інтеграл;
d) інша відповідь.
4. Формула інтегрування частинами у визначеному інтегралі
а) 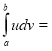
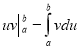 ; b)
; b) 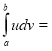
![]() ;
;
c) 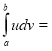
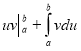 ; d) інша відповідь.
; d) інша відповідь.
5. Функція F(x) називається первісною для функції ![]() на проміжку
на проміжку
(a,b), якщо F(x) диференційовна на (a,b) і справджується рівність
а) ![]() ;
;
b) ![]() ;
;
c) ![]() ; d) інша відповідь.
; d) інша відповідь.
6. Метод інтегрування частинами застосовується тоді, коли під знаком інтеграла є
а) добуток функцій;
b) добуток складеної функції та похідної внутрішньої функції;
c) сума або різниця функцій;
d) інша відповідь.
7. Криволінійною трапецією називається
а) фігура, обмежена відрізком ОХ, відрізками прямих х=а і х=b і графіком функції![]() ;
;
b) фігура, обмежена відрізками прямих х=а і х=b і графіком функції![]() ;
;
c) невизначений інтеграл; d) інша відповідь.
8. Якщо на відрізку 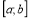 функція
функція 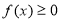 , то площа криволінійної
, то площа криволінійної
трапеції обчислюється за формулою
а) ![]() ; b)
; b) 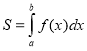 ;
;
c) 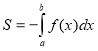 ; d) інша відповідь.
; d) інша відповідь.
9. Визначений інтеграл знаходять за формулою:
а) 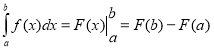 ;
;
b) 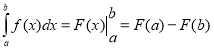 ;
;
c) 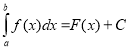 ; d) інша відповідь
; d) інша відповідь
10. Якщо на відрізку ![]() функція
функція ![]() , то площа криволінійної
, то площа криволінійної
трапеції обчислюється за формулою:
а) 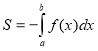 ; b)
; b) 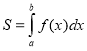 ;
;
c) ![]() ; d) інша відповідь.
; d) інша відповідь.
11. Якщо ![]() для
для ![]() , то
, то
а) 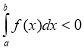 ; b)
; b) 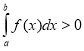 ;
;
с) визначити неможливо; d) інша відповідь.
12. Якщо фігура обмежена лініями функцій ![]() і
і ![]() (причому
(причому ![]() ), то площа фігури обчислюється за формулою:
), то площа фігури обчислюється за формулою:
а) 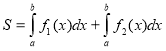 ; b)
; b) 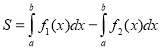 ;
;
c) 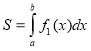 ; d) інша відповідь.
; d) інша відповідь.
Додаток Г
Таблиця-тест
Заповнити таблицю-тест, у клітках якої потрібно знаком «+» указати відповідність визначеного інтегралу та його значення
|
відповіді
завдання |
-4 |
0 |
|
|
1 |
2 |
4 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Додаток Д
Критерії оцінки тестів
Виконання тесту менш ніж на 60% вважається не виконаним і студент отримує незадовільну оцінку. Задовільна оцінка виставляється студенту, який дав правильну відповідь на 60%-75% питань тесту. Оцінка добре буде виставлена студентам, які вірно відповіли на 75% -90% відповідей. Студенти, що вірно виконали 90-100% тестових завдань отримують відмінну оцінку.
При оцінюванні тестових завдань використовують наступну шкалу оцінювання:
|
Кількість виконаних завдань |
1-6 |
7-8 |
9-10 |
11-12 |
|
оцінка |
2 |
3 |
4 |
5 |
Ключ до тесту
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
а |
с |
b |
с |
а |
а |
b |
а |
а |
а |
b |
Кожне завдання таблиці –тесту оцінюється в 1 бал, тобто максимальна оцінка, яку може отримати студент -4бали.
Еталон відповіді на питання таблиці-тесту.
|
відповіді завдання |
4 |
0 |
|
|
1 |
2 |
4 |
10 |
|
|
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
В ході проведення заняття студент заповнює картку самоконтроля. За кожен етап практичного заняття студент може отримати 1бал. Максимальна кількість -5 балів. Викладач заносить власну оцінку студента у відомість та враховує її при виставлені середнього балу
Додаток Е
Інструкційна карта
до практичного заняття
з дисципліни “Вища математика”
Тема: Інтегральне числення та диференціальні рівняння.
Тема практичного заняття: Обчислення визначеного інтегралу.
Мета: Сформувати вміння та навички обчислювати визначений інтеграл.
Методичне забезпечення: картки самоконтролю, інструкційні карти, інтелектуальні картки.
Методичні вказівки:
1. Правила для обчислення інтегралів.
1.![]()
2.![]()
3.![]() ;
;
2. Властивості визначеного інтегралу.
- Властивість лінійності: Постійний множник можна виносити за знак інтеграла:
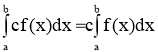
- При перестановці меж міняється знак інтеграла:
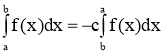
- При рівних межах a=b, інтеграл дорівнює нулю:
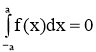
- Властивість аддитивности: Відрізок інтегрування можна розбивати на частині: a<c<b для будь-яких a;b;c
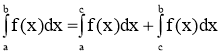
- Інтеграл від алгебраїчної суми функцій дорівнює сумі інтегралів від усіх доданків:
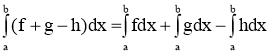
3. Таблиця інтегралов.
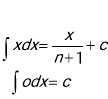
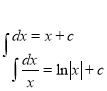
![]()
![]()
![]()
![]()
![]()
![]()
![]()
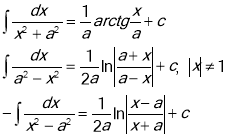
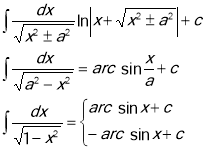
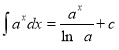
Формула Ньютона-Лейбніца 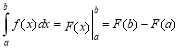
Методи інтегрування
- Метод безпосереднього інтегрування.
- Метод підстановки
Нехай функція![]() неперервна на [a;b], а функція
неперервна на [a;b], а функція![]() неперервно диференційовна функція на
неперервно диференційовна функція на ![]() , причому
, причому ![]() , то
, то 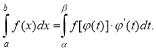
3. Метод інтегрування частинами
Формула інтегрування частинами: 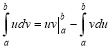 .
.
Порядок виконання практичної роботи
- Колективне розв’язування задач
-
Обчислити визначений інтеграл методом безпосереднього інтегрування
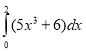
2)Обчислити визначений інтеграл методом підстановки 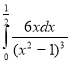
3) Обчислити визначений інтеграл методом інтегрування частинами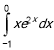
4) Тіло рухається прямолінійно з швидкістю ![]() м/с. Знайти шлях, пройдений тілом за перші 3 с.
м/с. Знайти шлях, пройдений тілом за перші 3 с.
2. Дослідити можливість застосування визначеного інтегралу до розрахунку економічних показників (представлення групових проектів студентів)
Самостійна робота студентів.
Обчислити визначений інтеграл:
1.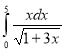
2.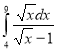
3.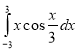
4.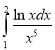
5.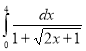
6.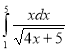
7.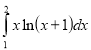
8.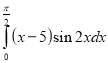
9.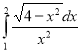
10.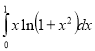
11.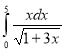
12.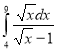
13.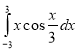
14.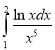
15.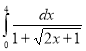
16.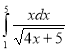
17.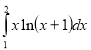
18.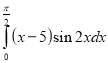
19.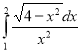
20.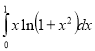
21.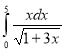
22.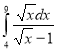
23.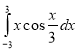
24.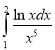
25.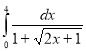
26.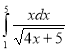
27.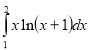
Домашнє завдання
Знайти визначені інтеграли, використовуючи три метода інтегрування.
1. 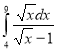 ; 2.
; 2.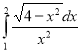 ; 3.
; 3. 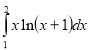
Додаток Ж
Критерії оцінки знань студентів
При виставленні оцінки студенту враховується :
- правильність виконання домашнього завдання;
- правильність виконання завдань тесту з теорії;
- правильність виконання завдань із таблиці-тесту;
- робота біля дошки;
- самостійність роботи;
- уміння застосувати знання в нестандартній ситуації.
Знання студентів оцінюються з урахуванням самостійної оцінки студентів за домашнє завдання, тест та усних відповідей, а також оцінки за самостійну роботу, яку оцінює викладач.
Оцінка «відмінно» виставляється якщо студент:
- Відмінно виконав домашнє завдання;
- Правильно вказав зв’язки між інтегралом та його первісною.
- дає повні, правильні і логічні усні відповіді;
- повною мірою володіє методикою знаходження визначених інтегралів;
- відмінно виконав самостійну роботу.
Оцінка «добре» виставляється якщо студент:
- не допускав істотних неточностей у відповідях і при розв’язанні завдань.
- добре або відмінно виконав самостійну роботу.
- не досить активно брав участь у колективній роботі та фронтальному опитуванні.
Оцінка «задовільно» виставляється якщо студент:
- пасивно брав участь у проведенні практичного заняття та окремих його частин;
- добре або задовільно виконав самостійну роботу;
- задовільно володіє теоретичними знаннями;
- певно застосовує таблицю інтегралів.
Оцінка «незадовільно» виставляється якщо студент:
- не брав участь у проведенні всіх етапів практичного заняття;
- давав неправильні відповіді на теоретичні питання;
- не володіє методикою рішення жодного з типів інтегралів;
- одержав незадовільну оцінку за самостійну роботу.
Відомість обліку роботи студентів групи за практичне заняття.
|
№ п/п |
Прізвище, ім’я, по-батькові студента |
Етапи проведення практичного заняття |
Середня оцінка студента |
|||||
|
Виконання тестових завдань |
Заповнення таблиці-тесту |
Колективне розв’язування практичних завдань |
Розробка та представлення презентації |
Виконання самостійної роботи |
Власна оцінка студента |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

про публікацію авторської розробки
Додати розробку
