Методична розробка "Розв’язування рівнянь з параметрами"
Міністерство освіти і науки, молоді та спорту України
Відділ освіти, молоді та спорту
Кодимської районної державної адміністрації
КЗ «Івашківський НВК «ЗШ І – ІІ ступенів-ДНЗ»
Кодимської районної ради Одеської області
Т. І. Бесараб
Розв’язування рівнянь з параметрами
Методичні рекомендації
для вчителів математики
загальноосвітніх навчальних закладів
Івашків
![]() 2018 рік
2018 рік
Розв’язування рівнянь з параметрами. Практико-орієнтований посібник.
Подано узагальнені матеріали, в яких описано різні види рівнянь з параметрами та методи їх розв’язування.
Специфіка задач із параметрами полягає в тому, що вони охоплюють усі теми алгебри, тому є унікальним засобом для систематизації й узагальнення навчальних досягнень учнів. Високий рівень абстрагування та алгоритмізації, що містять задачі з параметрами, розвиває навички застосування евристичних, дослідницьких прийомів роботи, вміння встановлювати причинно-наслідкові зв’язки, культуру мислення, ініціативу, творчість, а також забезпечити інтелектуальний розвиток особистості.
Посібник рекомендовано вчителям математики для використання на уроках алгебри, факультативних заняттях, під час підготовки учнів до математичних олімпіад та конкурсів,студентам педвузів та старшокласникам, які цікавляться математикою і готуються до ЗНО.
Автор посібника:
Бесараб Т. І. – вчитель–методист, учитель математики комунального закладу « Івашківський НВК «ЗШ І-ІІ ступенів - ДНЗ».
Рецензенти:
Джуган Галина Михайлівна – учитель – методист КЗ «Кодимська загальноосвітня школа І – ІІІ ступенів» Кодимської районної ради Одеської області
Відповідальна за випуск:
Ворсуляк Галина Костянтинівна, методист КУ «Кодимський РМК з питань освіти»
![]()
Метою цього посібника є формування в читачів мислення розгалудженя, елементарних навичок роботи з параметрами, розвиток графічної культури, творчого мислення.
Вступ……………………………………………………………………………..4
- Поняття про рівняння з параметрами…………………………………..6
2. Лінійні рівняння з параметрами…………………………………………..7
3. Дробово-раціональні рівняння з параметрами…………………………11
4 . Квадратні рівняння з параметрами……………………………………...15
4. 1. Існування коренів квадратного рівняння та їх кількість………….15
4.2. Існування коренів певних знаків………………………………………..18
4.3. Існування коренів, що задовольняють певні умови……………….21
5. Графічний спосіб розв’язування рівнянь………………………..24
- Що потрібно знати і чим користуватись…………………………………24
5.2. Приклади розв’язування рівнянь……………………………………… 27
Висновки ……………………………………………………………….…. 33
Список використаних джерел ……………………………………...........34
ВСТУП
Одним із найважливіших показників ефективності навчання у школі є забезпечення розвитку розумових здібностей учня. Стосовно математики можна сказати, що сам процес її вивчення повинен приводити до вміння логічно, доказово мислити, творчо, а не стереотипно, підходити до розв’язання будь-якої задачі. Справжня ситуація в школі така: більшість завдань розв’язується за певними алгоритмами, і швидке їх розв’язання зазвичай залежить від знання формул і вміння їх застосовувати. Тому завдання вчителя полягає в тому, щоб активізувати розумову та дослідницьку діяльність учнів.
Великим потенціалом у розвитку дослідницьких умінь- таких, як уміння спостерігати, аналізувати, висувати і доводити гіпотезу, узагальнювати, безумовно, є завдання з параметрами (зокрема, рівняння з параметрами).
Для розв'язування рівнянь з параметрами необхідне вміння проводити розгалуджені логічні побудови. При цьому потрібно чітко і послідовно стежити за збереженням рівносильності розв'язуваних рівнянь, враховувати області визначення виразів, які до них входять. Використання стандартних методів при виконанні таких завдань іноді призводить до необхідності виконання дуже громіздких обчислень, що суттєво ускладнює розв'язання. Така ситуація, як правило, сприяє початку творчих пошуків, дослідження, спрямованого на знаходження найбільш раціонального, найбільш “красивого” способу розв’язання. Крім того, учні, які володіють методами розв’язання завдань з параметрами, будуть більш творчо підходити до будь-якої задачі.
Для успішної самореалізації особистості у динамічному соціальному середовищі і достатньої для продовження навчання у вищих закладах освіти за спеціальностями, або безпосередньо пов’язаними з математикою, або за спеціальностями, де математика відіграє роль апарату для вивчення й аналізу закономірностей реальних явищ і процесів. Досягнення зазначеної мети забезпечується виконанням таких завдань:
формування в учнів наукового світогляду, уявлень про ідеї та методи математики, її ролі у пізнанні дійсності, усвідомлення математичних знань як невід’ємної складової загальної культури людини, необхідної умови повноцінного життя в сучасному суспільстві; стійкої позитивної мотивації до навчання;
оволодіння учнями мовою математики в усній та письмовій формах, системою математичних знань, навичок і умінь, потрібних у повсякденному житті та майбутній професійній діяльності, достатніх для успішного оволодіння іншими освітніми галузями знань і забезпечення неперервності освіти;
інтелектуальний розвиток особистості, передусім розвиток в учнів логічного мислення і просторової уяви, алгоритмічної, інформаційної та графічної культури, пам’яті, уваги, інтуїції;
громадянське, екологічне, естетичне виховання та формування позитивних рис особистості;
формування життєвих і соціально-ціннісних компетентностей учня.
Глибока, багата ідеями і методами змістовно-методична лінія задач з параметрами якнайкраще дозволяє розвивати активну творчу діяльність учня, його системне мислення, підготувати його до розв’язання дійсно творчих завдань, які з часом перед ним поставить саме життя.
Як показує практика, у завданнях ЗНО, на олімпіадах з математики пропонуються завдання з параметром . Але в шкільному курсі, як правило, недостатньо уваги приділяють таким задачам. Природньо, що у дітей виникають труднощі. Матеріал даного посібника саме і призначений для того, щоб дати теоретичне обґрунтування та на конкретних прикладах показати методи розв’язування рівнянь з параметрами.
Розв’язування рівнянь – одне з основних завдань алгебри, а рівнянь з параметрами – це ще й складне завдання.
Метою даного методичного посібника є надати методичні рекомендації вчителям щодо викладання даної теми.
1. Поняття про рівняння з параметрами.
Рівнянням з параметрами називають рівняння виду: f(х;![]()
де х – шукане невідоме, ![]() змінні параметри.
змінні параметри.
Розв’язати рівняння з параметрами означає, що для кожного значення параметра треба встановити, чи має рівняння розв’язки, і якщо має, то знайти ці розв’язки, що як правило, залежать від параметра.
Типи рівнянь з параметрами:
- розв’язування рівняння для будь-якого значення параметра;
- знаходження значень параметра, при яких рівняння має розв’язки;
- знаходження значень параметра, при яких рівняння має вказану кількість розв’язків;
- знаходження значень параметра, при яких розв’язки рівняння задовoльняють вказану умову.
Методи розв’язування:
- аналітичний;
- графічний.
При розв’язуванні рівнянь аналітичним способом можна сформулювати деякі загальні положення, дотримання яких дає певні орієнтири в процесі досліджень. А саме:
– знайти область допустимих значень параметрів ![]() ;
;
– розв’язати рівняння відносно х і представити х у вигляді функції від параметрів: х =![]() ;
;
– визначити для яких допустимих значень параметрів значення функції : х =![]() є розв’язком рівняння;
є розв’язком рівняння;
– розглянемо дане рівняння f(х; ![]() для таких допустимих параметрів при яких його неможливо розв’язати відносно цих значень параметрів, при яких його неможливо розв’язати відносно х; визначити чи має дане рівняння при цих значеннях параметрів розв’язки і якщо має, то які.
для таких допустимих параметрів при яких його неможливо розв’язати відносно цих значень параметрів, при яких його неможливо розв’язати відносно х; визначити чи має дане рівняння при цих значеннях параметрів розв’язки і якщо має, то які.
2. Лінійні рівняння з параметрами. Рівняння виду ах = в, де х – невідома, а і в параметри, називається лінійним рівнянням з параметрами.
![]() Розглянемо лінійні рівняння
Розглянемо лінійні рівняння
![]()
![]()
![]()
![]()
![]()
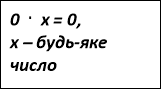


![]()
![]()
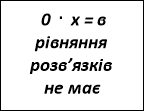
Дослідження та розв’язання лінійних рівнянь з параметрами. Приклад 1. Розв’язати рівняння: 5а(а![]() 4)х=а
4)х=а![]() 4. Розв’язання. Знайдемо ті значення параметра, які перетворюють у нуль коефіцієнт при х:
4. Розв’язання. Знайдемо ті значення параметра, які перетворюють у нуль коефіцієнт при х:
5а(а![]() 4)=0
4)=0
а=о, а=4 Якщо а=о, то рівняння матиме вигляд х![]() – коренів немає. Якщо а=4, то х
– коренів немає. Якщо а=4, то х![]() , х – будь-яке число. Якщо а
, х – будь-яке число. Якщо а![]() а
а![]() , то х=
, то х=![]() =
=![]() .
.
Відповідь: якщо а=о, то коренів немає; якщо а=4, то, х – будь-яке число; якщо а![]() а
а![]() , то х=
, то х=![]() .
.
Приклад 2. Розв’язати рівняння:
![]() Розв’язання.
Розв’язання.
![]() . Запишемо рівняння у вигляді
. Запишемо рівняння у вигляді
(а – 5)(а + 5)х = (а + 5)(а – 2). Знайдемо ті значення параметра , які перетворюють у нуль коефіцієнт при х: (а – 5)(а + 5)=0; а = 5, а = – 5.
Якщо а = 5, то х![]() немає розв’язків. Якщо а = – 5, то 0
немає розв’язків. Якщо а = – 5, то 0![]() , х – будь-яке число. Якщо а
, х – будь-яке число. Якщо а![]() а
а![]() , то х=
, то х=![]() .
.
Відповідь: якщо а = 5, то рівняння немає розв’язків; якщо а = – 5, то х – будь-яке число ; якщо а![]() а
а![]() , то х=
, то х=![]() .
.
Приклад 3. Розв’язати рівняння: (![]() – 6)х = (5х+ 2)а + 2. Розв’язання.
– 6)х = (5х+ 2)а + 2. Розв’язання.
Перейдемо до рівнянь-наслідків:
![]() – 6х = 5ах + 2а +2
– 6х = 5ах + 2а +2
![]() – 6х – 5ах = 2а+2
– 6х – 5ах = 2а+2
![]() – 5а – 6)х = 2а+2
– 5а – 6)х = 2а+2
(а + 1)(а – 6)х = 2(а + 1) Коефіцієнт при х дорівнює нулю, якщо а = – 1 або а = 6. Якщо а = –1, то 0![]() , х – будь-яке число. Якщо а = 6, то х
, х – будь-яке число. Якщо а = 6, то х![]() розв’язків немає. Якщо а
розв’язків немає. Якщо а![]() а
а![]() , то х=
, то х=![]() .
.
Відповідь: якщо а = –1, то х – будь-яке число; якщо а = 6, то розв’язків немає; якщо а![]() а
а![]() , то х=
, то х=![]() .
.
Приклад 4. Для якого значення параметра а число 4,5 є рівняння
х – 3 = а + 2 ?
Розв’язання.
Оскільки число 4,5 – корінь рівняння х – 3 = а + 2, то воно перетворює рівняння в правильну рівність
4,5 – 3 = а +2
а +2 =1,5
а = 1,5 – 2
а = – 0,5.
Відповідь: а = – 0,5. Приклад 5. Для яких значень а рівняння (![]() – 9)х = а – 3 не має розв’язків?
– 9)х = а – 3 не має розв’язків?
Розв’язання.
Рівняння не має розв’язків тоді, коли коефіцієнт при х дорівнює нулю, а вираз, що знаходиться у правій частині рівняння, не дорівнює нулю, то має місце система:
![]()
![]() звідки а = – 3
звідки а = – 3
Відповідь: а = – 3. Приклад 6. Знайти всі цілі корені рівняння ах = а + 5х, які кратні трьом (а – будь-яке ціле число, що не дорівнює 5).
Розв’язання.
ах = а + 5х
(а – 5)х = а . Оскільки а![]() то х=
то х=![]() . За умовою корені повинні бути кратні 3, тобто
. За умовою корені повинні бути кратні 3, тобто ![]() = 3k, де k
= 3k, де k![]()
а =3k (а – 5)
а =3аk –15k
а (1 – 3k ) = –15k
а = ![]()
Відповідь: х=![]() для а =
для а = ![]() , k
, k![]()
Приклад 7. Визначити для яких значень а рівняння
(х – 1)(а – 2) = 1
Матиме розв’язок, що належить інтервалу (1;2).
Розв’язання. Дане рівняння має розв’язок, якщо а![]() тобто а
тобто а![]()
х – 1=![]()
х = 1 +![]()
х = ![]()
х = ![]()
За умовою 1 ![]()
![]()
![]() .
.
Перейдемо до системи:
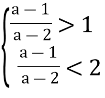
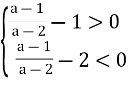
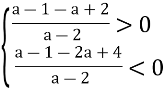
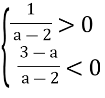
![]() звідки а
звідки а![]()
Відповідь: х = ![]() для а
для а![]()
3. Дробово-раціональні рівняння з параметрами Приклад 1. Розв’язати рівняння:
![]() =
=![]() .
.
Розв’язання.
х(а + 4) = 0 ОДЗ параметра: а![]() ОДЗ невідомого: х
ОДЗ невідомого: х ![]() Зведемо дане рівняння до лінійного:
Зведемо дане рівняння до лінійного:
![]() .
.
![]() .
.
ах +х – 3а – 12 +7 = 0
(а + 1)х = 3а +5
а = - 1 Якщо а = – 1, то 0![]() розв’язків немає. Якщо а
розв’язків немає. Якщо а![]() х =
х =![]() Перевіримо чи немає таких значень при яких х = 0:
Перевіримо чи немає таких значень при яких х = 0: ![]() = 0
= 0
3а = – 5
а =![]() , а =
, а = ![]() . Якщо а =
. Якщо а = ![]() то х = 0. Відповідь: якщо а
то х = 0. Відповідь: якщо а![]() , а
, а ![]() 4, а
4, а ![]() то х =
то х =![]() ; якщо а
; якщо а![]() , а =
, а = ![]() , то рівняння немає розв’язків; якщо а
, то рівняння немає розв’язків; якщо а![]() , то рівняння не має смислу.
, то рівняння не має смислу.
Приклад 2. Розв’язати рівняння:
![]() .
.
Розв’язання. ОДЗ невідомого: х![]() х
х ![]()
Зведемо дане рівняння до лінійного:
(а – 5)(х – 2) – (7 – 3а)(х + 1) = 26х – 5
(а – 5)х – (7 – 3а)х – 26х = 2(а – 5) + (7+ 3а) – 5
(а – 5 – 7 – 3а – 26)х = 5а – 8
( – 2а – 38)х = 5а – 8
– 2а – 38 = 0
а = – 19
![]() 8 – 5а = – 2а – 38 ОДЗ невідомого:
8 – 5а = – 2а – 38 ОДЗ невідомого: ![]()
– 3а = –46
а = ![]() = 15
= 15![]()
-
х = 2
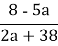 = 2
= 2
8– 5а = 4а + 76
– 9а = 68
а = ![]() = – 7
= – 7![]()
Відповідь: якщо а = – 7![]() , а = – 19, а = 15
, а = – 19, а = 15![]() , то рівняння немає розв’язків;
, то рівняння немає розв’язків;
якщо а ![]() – 7
– 7![]() , а
, а![]() – 19, а
– 19, а ![]() 15
15![]() , то рівняння має один розв’язок то х =
, то рівняння має один розв’язок то х = ![]() .
.
Приклад 3. Розв’язати рівняння:
![]() =
=![]() .
.
Розв’язання.
ОДЗ: х ![]() х
х ![]() Зведемо дане рівняння до лінійного:
Зведемо дане рівняння до лінійного:
(х + а)![]() =
= ![]() (х – а)
(х – а)
![]()
(1 – 2а +![]() – 1 – 2а –
– 1 – 2а – ![]() ) х = – (1 + 2а +
) х = – (1 + 2а +![]() 1 – 2а –
1 – 2а – ![]() )а
)а
4ах = 2![]()
а = 0
Якщо а = 0, то 0![]() будь-яке число. Якщо а
будь-яке число. Якщо а![]() х =
х =![]()
З’ясуємо для яких значень а х =![]() а
а
-
х = а
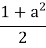 = а
= а
1 – 2а +![]() = 0
= 0
![]() = 0
= 0
а = 1
-
х = – а
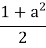 = – а
= – а
1 + 2а +![]() = 0
= 0
![]() = 0
= 0
а = – 1 Відповідь: якщо а =![]() то рівняння не має розв’язків; якщо а = 0, то
то рівняння не має розв’язків; якщо а = 0, то ![]() будь-яке число. якщо а
будь-яке число. якщо а![]() а
а![]() , то х =
, то х =![]()
Приклад 4. Для яких значень параметра а рівняння ![]() має цілі корені?
має цілі корені?
Розв’язання.
![]() ОДЗ параметра: а
ОДЗ параметра: а![]() Зведемо дане рівняння до лінійного:
Зведемо дане рівняння до лінійного:
(а -1)(х +1) = 2(2а - 1)
Якщо а ![]() 1, то х +1 =
1, то х +1 = ![]()
х = ![]() – 1
– 1
х = ![]()
х = ![]() За умовою х – ціле число, тобто х = k, k
За умовою х – ціле число, тобто х = k, k![]() , тому
, тому
![]() = k,
= k,
3а – 1 = аk – k
3а – аk = 1– k
(k – 3)а = k – 1 Якщо k![]() , то а =
, то а = ![]() і а
і а![]() 1. Перевіримо умову а
1. Перевіримо умову а ![]() тоді
тоді ![]() , 2k – 2
, 2k – 2 ![]() k – 3, k
k – 3, k ![]() . Отже, х =
. Отже, х = ![]() , якщо а =
, якщо а = ![]() , k
, k![]() , k
, k![]() , , k
, , k ![]() .
.
Відповідь:
х = ![]() для а =
для а = ![]() .
.
4. Квадратні рівняння з параметрами
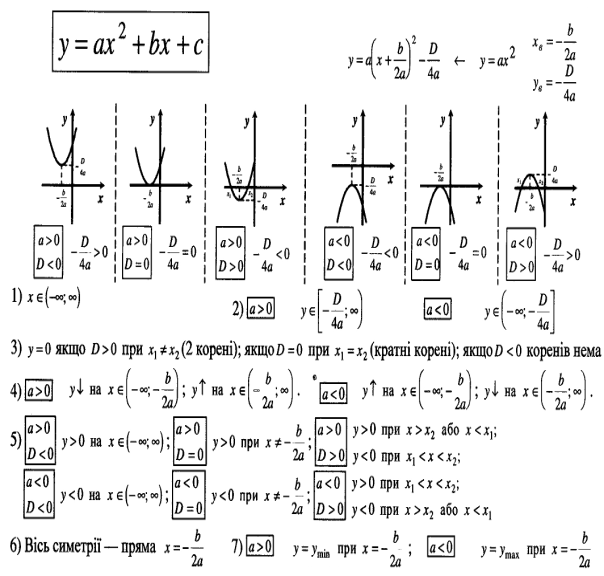
4. 1. Існування коренів квадратного рівняння та їх кількість. Рівняння виду а![]() + bx +c = 0, x - змінна a, b, c – параметри, а
+ bx +c = 0, x - змінна a, b, c – параметри, а![]() називається квадратним рівняння з параметрами. Розглянемо квадратне рівняння.
називається квадратним рівняння з параметрами. Розглянемо квадратне рівняння.
![]()

 а=0 а
а=0 а![]()
![]()
![]()
![]()
![]()
![]()

![]()
b=0 b![]() D
D![]() D=0 D
D=0 D![]()



![]()
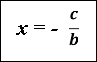
![]()
![]()
c=0 c![]()
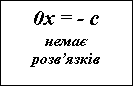
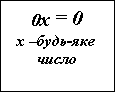
Приклад 1. Розв’язати рівняння
3(2а – 1![]() ) – 2(а + 1)х + 1 = 0.
) – 2(а + 1)х + 1 = 0.
Розв’язання. Якщо а =![]() , то дане рівняння перетворюється в лінійне рівняння:
, то дане рівняння перетворюється в лінійне рівняння:
0![]() – 2(
– 2(![]() + 1) х + 1 = 0
+ 1) х + 1 = 0
– 3х + 1 = 0 х =![]() Якщо а
Якщо а ![]() , то дане рівняння є квадратним. Знайдемо дискримінант :
, то дане рівняння є квадратним. Знайдемо дискримінант :
Д = 4![]()
= 4![]()
Д =0, якщо а =2. Тоді дане рівняння набирає вигляду:
![]()
(![]() = 0
= 0
х =![]() Д
Д![]() , якщо а
, якщо а![]() Дане рівняння має два корені:
Дане рівняння має два корені:
х =![]()
![]() =
=![]() =
= ![]() =
= ![]()
![]() =
=![]() =
= ![]() =
= ![]() =
=![]() Відповідь: якщо а =
Відповідь: якщо а = ![]() , а = 2, то х=
, а = 2, то х=![]() якщо а
якщо а ![]() , а
, а ![]() 2,
2, ![]() то рівняння має два різних корені х =
то рівняння має два різних корені х =![]() або х =
або х = ![]() .
.
Приклад 2. Знайти всі значення параметра а, для яких рівняння
( а – 2)![]() не має дійсних коренів.
не має дійсних коренів.
Розв’язання . Якщо а – 2 = 0, а = 2, то 0![]() х + 2 = 0, 0
х + 2 = 0, 0![]() х = – 2. Отже, рівняння не має розв’язків. Якщо а
х = – 2. Отже, рівняння не має розв’язків. Якщо а ![]() 2, то рівняння є квадратним. Знайдемо дискримінант:
2, то рівняння є квадратним. Знайдемо дискримінант:
Д = 4(![]()
Рівняння не має розв’язків, якщо Д![]() :
:
![]() . Звідки а
. Звідки а ![]() (2; 4) .
(2; 4) .
Відповідь: а ![]() (2; 4) .
(2; 4) .
Приклад 3. Розв’язати рівняння
(![]() +1)х2+2
+1)х2+2![]() х+
х+![]() -2=0.
-2=0.
Розв’язання.
1). Якщо ![]() +1= 0 тобто
+1= 0 тобто ![]() = -1, то задане рівняння буде мати вигляд: -2х – 3 = 0, тобто х =-
= -1, то задане рівняння буде мати вигляд: -2х – 3 = 0, тобто х =-![]()
2). Якщо ![]() +1≠0 (
+1≠0 (![]() ≠ -1), то одержимо квадратне рівняння, дискримінант якого D=4(
≠ -1), то одержимо квадратне рівняння, дискримінант якого D=4(![]() +2). Тому розглянемо три випадки:
+2). Тому розглянемо три випадки:
а) якщо D=0, тобто 4(![]() +2) = 0, то
+2) = 0, то ![]() = -2 i х = -2;
= -2 i х = -2;
б) якщо D<0, тобто 4(![]() +2) < 0 (
+2) < 0 (![]() < -2), то коренів немає;
< -2), то коренів немає;
в) якщо D>0: 4(![]() +2) > 0;
+2) > 0; ![]() > -2 і
> -2 і ![]() ≠ -1, тобто
≠ -1, тобто
-2 < ![]() < -1 і
< -1 і ![]() > -1, то квадратне рівняння має два різні корені:
> -1, то квадратне рівняння має два різні корені:
х1=![]() ; х2=
; х2=![]()
Відповідь: якщо ![]() =-1, то х=-
=-1, то х=-![]() ;
;
якщо ![]() ≠-1 і
≠-1 і ![]() ≥-2, то х=
≥-2, то х=![]() ;
;
Приклад 4. При яких значеннях параметра а рівняння
2ах2-4(![]() +1)х+4
+1)х+4![]() +1=0 має єдиний розв’язок?
+1=0 має єдиний розв’язок?
Розв’язання.
Оскільки в умові не сказано, що рівняння є квадратним, то спочатку розглянемо випадок а=0, тобто рівняння -4х+1=0, яке має один розв’язок х =![]() .
.
Решту значень а отримаємо з умови D=0:
D=16(![]() +1)2-4.2
+1)2-4.2![]() . (4
. (4![]() +1),
+1),
2![]() 2-3
2-3![]() -2=0;
-2=0; ![]() 1= -
1= -![]() і
і ![]() 2 =2.
2 =2.
Відповідь: при -![]() , 0; 2.
, 0; 2.
4.2 Існування коренів певних знаків
Для квадратного рівняння
а![]() + bx +c = 0, де а
+ bx +c = 0, де а![]() мають місце такі твердження:
мають місце такі твердження:
- Рівняння має два додатні корені, якщо виконуються умови:
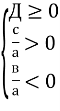
- Рівняння має два від’ємні корені, якщо виконуються умови:
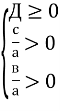
- Рівняння має корені різних знаків, якщо виконуються умови:
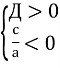
- Рівняння має два різні додатні корені, якщо виконуються умови:
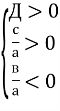
- Рівняння має два від’ємні корені, якщо виконуються умови:
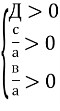
Приклад 1. Для яких значень параметра т обидва корені рівняння
(![]() , додатні?
, додатні?
Розв’язання Оскільки рівняння має два корені, то т – 2![]() , звідки т
, звідки т ![]() Для того, що корені були додатні, мають виконуватися умови:
Для того, що корені були додатні, мають виконуватися умови:
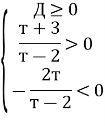
![]()
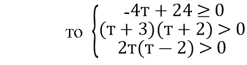
тобто 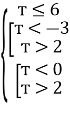
Звідки т![]() .
.
Відповідь: ![]()
Приклад 2. Знайти найменше ціле значення параметра т, для якого рівняння
(![]() має
має ![]()
![]()
![]() , т
, т ![]() .
.
Якщо рівняння має два корені різних знаків, то виконуються умови:
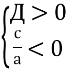
Оскільки Д = (![]() 2 - 4),
2 - 4),
Д = 4(т + 1)(т + 3).
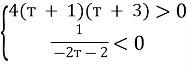
![]()
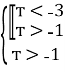
Звідки т![]()
т =0 - це найменше число на цьому проміжку. Відповідь: 0.
Приклад 3. Знайти всі значення параметра ![]() , при кожному з яких рівняння
, при кожному з яких рівняння
(![]() +1)х2-(1-2
+1)х2-(1-2![]() )х+
)х+![]() +1=0 має два різні корені.
+1=0 має два різні корені.
Розв’язання.
Оскільки за умовою задане рівняння має два різних корені, то воно є квадратним, отже, ![]() +1≠0.
+1≠0.
Знайдемо дискримінант: D=(1-2![]() )2-4(
)2-4(![]() +1)2 = -12
+1)2 = -12![]() – 3.
– 3.
Щоб рівняння мало два різні корені, дискримінант повинен бути додатним, тобто -12![]() – 3 > 0,
– 3 > 0, ![]() < -
< -![]() (
(![]() ≠-1).
≠-1).
Тоді: х1=![]() х2=
х2=![]()
Відповідь: при ![]() є (-∞;-1)(-1;-
є (-∞;-1)(-1;-![]() ).
).
4 .3. Існування коренів, що задовольняють певні умови.
За теоремою Вієта між коренями ![]() і
і ![]() квадратного рівняння
квадратного рівняння
а![]() + bx +c = 0 та його коефіцієнтами існують співвідношення:
+ bx +c = 0 та його коефіцієнтами існують співвідношення:
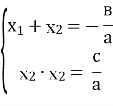
За допомогою цих співвідношень розв’язується багато задач.
Приклад 1. Для яких значень а корені рівняння
11![]() задовольняють умову
задовольняють умову ![]()
![]() = 2?
= 2?
Розв’язання. Для того, щоб рівняння мало два корені, має виконуватись умова Д ![]()
Д = 64 – 44а
64 – 44а![]()
а![]() , а
, а![]() , За теоремою Вієта і умовою складаємо систему рівнянь:
, За теоремою Вієта і умовою складаємо систему рівнянь:
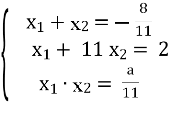
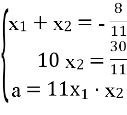
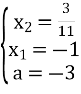
Відповідь: – 3.
Приклад 2. При яких значеннях параметра т сума квадратів коренів рівняння
4![]() дорівнює 22,5?
дорівнює 22,5?
Розв’язання.
Нехай ![]() і
і ![]() – корені даного рівняння. Тоді за умовою
– корені даного рівняння. Тоді за умовою
![]()
(![]() (1) Але за теоремою Вієта
(1) Але за теоремою Вієта ![]()
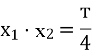
Підставивши у формулу (1), дістанемо 49 = 22,5 + ![]() ,звідки т = 53.
,звідки т = 53.
Але це число не можна вважати відповіддю, оскільки воно було одержано в результаті припущення, що корені існують, тобто дане рівняння має розв’язок. Але при т = 53 дискримінант утвореного рівняння 4![]() від’ємний і рівняння розв’язків немає.
від’ємний і рівняння розв’язків немає.
Відповідь: таких значень немає.
Приклад 3. При якому значенні параметра ![]() один з коренів рівняння
один з коренів рівняння
х2-(2![]() +1)х+
+1)х+![]() 2+2=0 вдвічі більший від іншого?
2+2=0 вдвічі більший від іншого?
Розв’язання.
За теоремою Вієта та умовою задачі отримуємо систему рівнянь: 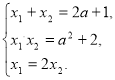
![]() Підставляючи значення х1 з третього рівняння в перше та друге, одержимо:
Підставляючи значення х1 з третього рівняння в перше та друге, одержимо:
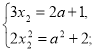
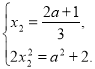
Отже, 2(![]() )2 = а2 + 2;
)2 = а2 + 2;
8![]() 2 + 8
2 + 8![]() + 2 = 9
+ 2 = 9![]() 2 + 18;
2 + 18;
а2 - 8![]() + 16 = 0;
+ 16 = 0;
(![]() -4)2 = 0;
-4)2 = 0;
![]() = 4 Відповідь: при
= 4 Відповідь: при ![]() = 4.
= 4.
Приклад 4. Визначити числове значення параметра ![]() , при якому сума квадратів коренів рівняння
, при якому сума квадратів коренів рівняння
х2-![]() х+
х+![]() - 2=0 буде найменшою.
- 2=0 буде найменшою.
Розв’язання.
За теоремою Вієта х1+х2=![]() ; х1
; х1![]() х2=
х2=![]() - 2.
- 2.
Крім того, х12+х22=(х1 +х2)2 -2х1х2=![]() 2-2(
2-2(![]() -2)=(
-2)=( ![]() -1)2+3.
-1)2+3.
Отриманий вираз набуває найменшого значення при ![]() =1.
=1.
Найменше значення цього виразу дорівнює 3.
Відповідь: при ![]() =1.
=1.
Приклад 5. Відомо, що ![]() , де х1 і х2 – корені рівняння х2+х+
, де х1 і х2 – корені рівняння х2+х+![]() =0. Визначити
=0. Визначити ![]() .
.
Розв’язання.
Оскільки ![]() , а за теоремою Вієта х1+х2=-1; х1х2=
, а за теоремою Вієта х1+х2=-1; х1х2=![]() , то
, то ![]()
Отже, ![]() = -6
= -6
Відповідь: ![]() = -6
= -6
Приклад 6. Визначити кількість цілих значень параметра m, при яких квадратне рівняння 2х2+mх+2m=0 не має дійсних коренів.
Розв’язання .
Рівняння не має дійсних коренів, якщо D<0.
Тому m2-4*2*2m<0; m2-16m<0; m(m-16)<0; m є (0;16).
Цілі значення: 1;2;3;4;5;……15
Відповідь: 15.
5.Графічний спосіб розв’язування рівнянь
Суть методу полягає в тому, що задачу зводять до з’ясування взаємного розташування графіків рівнянь що містять параметри по відношенню до графіків рівнянь які у своєму складі не містять параметрів.
Найчастіше графічно розв’язують ті задачі, де потрібно знайти кількість розв’язків, коли в задачі є «впізнавана функція», модуль.
До того ж в деяких випадках аналітичний метод розв’язування «тягне за собою» таку кількість систем і сукупностей, що в них дуже легко заплутатись. І тоді на допомогу приходить графіка.
Графічний – виключно красивий і наочний але не завжди доречний і потребує мистецтва роботи з графіками.
- Що потрібно знати і чим користуватись.
Прямі і кола.
Щоб розв’язувати графічно задачі з параметрами необхідно вміти будувати і перетворювати графіки функцій та залежностей. В цьому розділі – відомості про графіки функцій і залежностей, які найчастіше зустрічаються.
- Пряма y=kx+b
|
k – змінна b - const |
пряма«обертається» навколо точки (0;b) (рівняння прямої з полюсом) |
|
|
b – змінна k - const |
y=kxрухається вздовж осей координат
|
|
|
y=k1 x+b1 y=k2 x+b2
|
k1 = k2 |
прямі паралельні |
|
k1 k2 = - 1 |
прямі перпендикулярні |
|
- Коло (x-a)2 + (y-b)2=R2
|
a – змінна b – const R - const |
коло «рухається» вздовж осі Ох |
|
|
b – змінна a - const R - const |
коло «рухається» вздовж осі Оу |
|
|
a – const b – const R - змінна |
«сім’я» концентричних кіл з центром в точці (а;b) |
|
Коло і пряма: перетинаються (2 спільні точки), дотикаються(1спільна точка), не перетинаються (не мають спільних точок).
 Модуль.
Модуль.
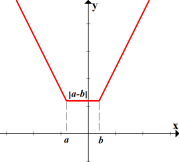
Графік функції виду у = |х - а| + |х -b|
«дно»: у = |а - b|
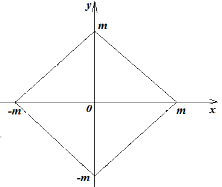
Графік залежності виду |х| + |у|= т – квадрат
|х - а| + |х -b|= т
|
a – змінна b – const т - const |
квадрат «рухається» вздовж осі Ох
|
|
b – змінна a - const т - const |
квадрат «рухається» вздовж осі Оу
|
|
a – const b – const т - змінна |
|
Квадратична функція і не тільки…
Про графік квадратичної функції написано багато. На мою думку цей конспект (посібник Г.В.Апостолова, В.В.Ясінський «Перші зустрічі з параметром»)– найкраще узагальнення відомостей про графік квадратичної функції. Але розділ називається «Квадратична функція і не тільки». Тож давайте дослідимо ще деякі випадки непрямого використання квадратичної функції на прикладах.
![]()
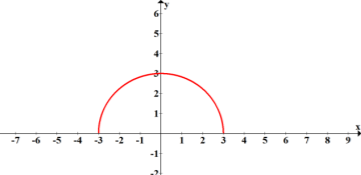 Графік функції – півколо з центром в (0;0), радіусом 3 (y ≥ 0)
Графік функції – півколо з центром в (0;0), радіусом 3 (y ≥ 0)
- . Приклади розв’язування рівнянь
Приклад 1. Знайдіть всі значення параметра а при якому рівняння має менше 4 коренів ![]()
![]()
Розв’язання
Запишемо рівняння в вигляді:![]()
Нехай f(x) = ![]() g(x)=
g(x)=![]()
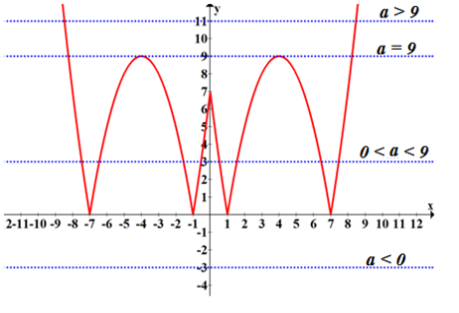
Схематично зобразимо графіки функцій f(x) та g(x).
Графік функції g(x)=![]() - пряма, паралельна осі Ох. Розв’язки рівняння – абсциси точок перетину графіків функцій.
- пряма, паралельна осі Ох. Розв’язки рівняння – абсциси точок перетину графіків функцій.
Пряма не перетне графік f(x), якщо а< 0 і якщо а>9, то пряма матиме з графіком менше чотирьох точок перетину (а саме дві).
Тобто, рівняння має менше 4 коренів коли ![]()
![]() Відповідь:
Відповідь:![]()
Приклад 2 . Розв’язати рівняння
Вказівка. Побудуємо графіки функцій у =![]() та у =
та у = ![]() .
.
Проведемо дослідження за допомогою графіків.
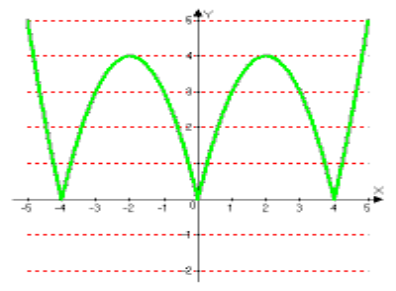
![]() Відповідь: 1)Якщо а<0, то коренів немає; 2)якщо а=0, то рівняння має два корені; 3)якщо 0<a<4, то рівняння має 6 коренів; 4)якщо а=4, то рівняння має 4 корені;
Відповідь: 1)Якщо а<0, то коренів немає; 2)якщо а=0, то рівняння має два корені; 3)якщо 0<a<4, то рівняння має 6 коренів; 4)якщо а=4, то рівняння має 4 корені;
5)якщо а>4, то рівняння має 2 корені.
Приклад 3 . Розв’язати рівняння
Вказівка. Побудуємо графіки функцій у =![]() та у =
та у = ![]() .
.
Проведемо дослідження за допомогою графіків.
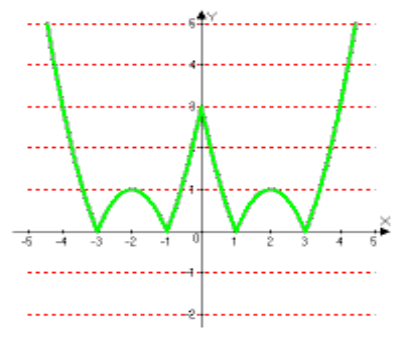
Відповідь: 1) Якщо а<0, то коренів немає; 2) якщо а=0, або 1<a<3,то рівняння має чотири корені; 3)якщо 0<a<1, то рівняння має вісім коренів 4)якщо а=1, то рівняння має шість коренів; то рівняння має два корені; то рівняння має два корені; 5)якщо а=3, то рівняння має три корені; 6)якщо а>3, то рівняння має два корені.
Приклад 4. Знайти всі значення параметра а при яких найменше значення функції f(x) дорівнює найбільшому значенню функції 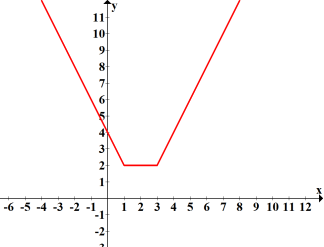 g(x).
g(x).
f(x)=|x - 1|+|x - 3|+a
g(x)=![]()
Розв’язання
Графік функції g(x)- парабола, вітки напрямлені вниз, найбільшого значення досягає в вершині х = 0; g(x)=![]()
f(x)=|x-1|+|x-3|+a
Побудуємо графік
у =|x-1|+|x-3|.
Найменше значення у = 2+a
Значить,
![]()
Відповідь:![]()
Приклад 5. Знайдіть усі значення параметра ![]() , при яких рівняння
, при яких рівняння
|х+1|+|х-2| =![]() має два розв’язки.
має два розв’язки.
Вказівка. Розглянути дві функції:
у1= |х+1|+|х-2| та у2 =![]() .
.
Побудувати графік функції
у1= |х+1|+|х-2|, тобто
у1= 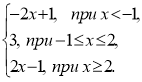
![]()
![]()
Розглянути різні випадки розташування прямої у2=![]() відносно
відносно
графіка функції у1, від чого і залежить кількість розв’язків рівняння:
при ![]() <3 рівняння коренів немає;
<3 рівняння коренів немає;
при ![]() =3: х є [-1;2];
=3: х є [-1;2];
при ![]() >3 рівняння має два корені.
>3 рівняння має два корені.
Відповідь: при ![]() >3 рівняння має два розв’язки.
>3 рівняння має два розв’язки.
Приклад 6. Розв’яжіть рівняння для всіх дійсних значень параметра а.
|x2 - 4|-|x2 - 9| = ![]()
Розв’язання
Розглянемо дві функції f(x)= |x2 - 4|-|x2 - 9| і g(x)=![]() .
.
Схематично зобразимо графік f(x).
Для цього знайдемо нулі модулів і знаки модулів на проміжках
Для х ≤ -3 або х ≥ 3, f(x)=5
Для -3< x <-2 і 2< x <3, f(x)=2х2- 13
Для -2< x <2f(x)= - 5

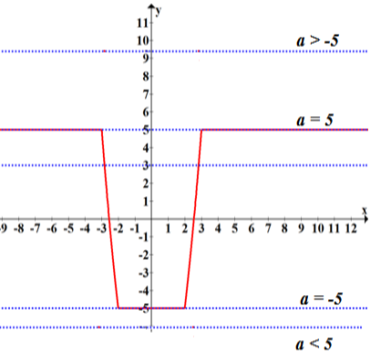
Відповідь: якщо![]() < -5 або
< -5 або![]() >5, то рівняння розв’язків не має;
>5, то рівняння розв’язків не має;
якщо ![]() = -5, то
= -5, то ![]() ;
;
якщо ![]() = 5, то
= 5, то ![]() ;
;
якщо ![]() то
то ![]() .
.
Приклад 7. Розв’яжіть рівняння для всіх дійсних значень параметра а
![]()
Розв’язання
Розглянемо дві функції f(x)= ![]() іg(x)=
іg(x)=![]()
Побудуємо графік функції f(x)= ![]() за допомогою геометричних перетворень
за допомогою геометричних перетворень
![]()
Графік g(x)=![]() - горизонтальна пряма, що рухається вгору-вниз по осі Оу.
- горизонтальна пряма, що рухається вгору-вниз по осі Оу.
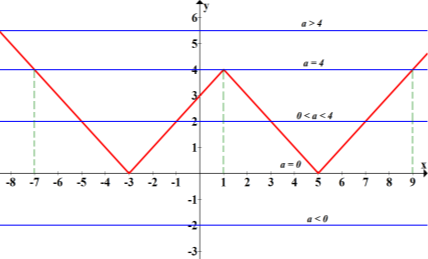
Відповідь: якщо ![]()
якщо ![]() ;
;
якщо ![]()
якщо ![]() ;
;
якщо ![]()
Приклад 8. Визначити кількість коренів рівняння | 2 | х | -1 | = ![]() залежно від параметра
залежно від параметра ![]() .
.
Вказівка. Побудуємо графіки функцій у = | 2 | х | -1 та у = ![]() .
.
Проведемо дослідження за допомогою графіків.
Відповідь: якщо ![]() < 0, то рівняння немає коренів;
< 0, то рівняння немає коренів;
якщо ![]() = 0, то рівняння має два корені;
= 0, то рівняння має два корені;
якщо ![]() є ( 0;1), то рівняння має чотири корені;
є ( 0;1), то рівняння має чотири корені;
якщо ![]() = 1, то рівняння має три корені;
= 1, то рівняння має три корені;
якщо ![]() > 1, то рівняння має два корені.
> 1, то рівняння має два корені.
Приклад 9. Знайдіть найбільше значення параметра a, при якому
рівняння |![]() − 3|x|− 4| = a має тільки чотири корені..
− 3|x|− 4| = a має тільки чотири корені..
Розв’язання:
Побудуємо графік функції y = |![]() − 3|x|− 4| і розглянемо, коли він буде мати рівно 4 точки перетину з прямою у=а.
− 3|x|− 4| і розглянемо, коли він буде мати рівно 4 точки перетину з прямою у=а.
При a < 0 точок перетину не існує,
при a = 0 їх буде дві, потім – чотири,
при a = 5 точок перетину буде 6,
та при деякому значенні a їх знову стане чотири.
Знайти це значення легко, якщо згадати, що даний графік був отриманий з параболи у=![]() − 3|x|− 4 відображенням від осі Оy та згинанням через вісь Ох. Отже, координата
− 3|x|− 4 відображенням від осі Оy та згинанням через вісь Ох. Отже, координата ![]() вершини параболи перейде саме в потрібне значення параметра а.
вершини параболи перейде саме в потрібне значення параметра а.
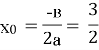
![]() - 4 = 6,25
- 4 = 6,25
Відповідь: 6,25.
ВИСНОВКИ
У роботі розглянуто типи рівнянь із параметрами, розкрито сутність
аналітичного, графічного методу , які використовуються для розв'язання
рівнянь .
Зрозуміло, що задачі з параметром – це специфічний тип завдань,
для розв’язання яких треба бути не лише добре обізнаним із основними
принципами та схемами розв’язування, а й вміти творчо підходити до
їх вирішення, мати розвинене логічне та критичне мислення.
Цей матеріал допоможе і значно полегшить роботу тим, кому доведеться
мати справу з дослідженням і розв'язуванням рівнянь з параметром,
дасть можливість знайти красивий і простий спосіб розв'язування
багатьох задач. Надіюсь, що матеріал посібника стане в нагоді
старшокласникам, які готуються до ЗНО самостійно чи навчаються на
підготовчих курсах у ВУЗах, учням старших класів при підготовці до
математичних олімпіад та вчителям для факультативних занять та для
підготовки учнів до ЗНО(поглиблений рівень).
Зокрема, розглянуті у посібнику завдання можуть бути використані при
вивченні тем: функції, многочлени, рівняння і нерівності.
Список використаних джерел
1. Заслонкіна Л.С. Задачі з праметрами.- Х.: Вид. Група
“Основа”, 2012.
2. Репета В.Л., Клешня Н.О., Репета В.А. , Задачі з
параметрами : Посібник для абітурієнтів, старшокласників.
За ред.: В.Т . Мовчана. - К. : НА О, 2008
3.Інтернет-ресурси.
4. П.І. Горнштейн “Задачі з параметрами” , Київ, РІА
“Текст”, 2007
5. Наук ово-методичний журнал “ Математика в школах
України”
6. Н.І. Затула, А.М. Зуб, Г .І. Коберник, А.Ф. Нещадим “
Математика “, нав чальний посібник, Київ, 2006
7. Апостолова Г .В., Ясінський В.В. Перші зустрічі з
параметрами. - К.: факт , 2008


про публікацію авторської розробки
Додати розробку
