Методична розробка «Розвиток творчих компетентностей учнів на уроках математики через використання інтерактивних методик і технологій навчання».

Про матеріал

Робота розкриває особливості, вимоги, методи та прийоми, результати, ефективність навчання, спрямованого на розвиток особистості учня, дає конкретні рекомендації щодо проведення уроків математики з використанням інтерактивних методик і технологій навчання. Методичну розробку можна використовувати для підготовки уроків з використанням інтерактивних методик і технологій навчання, як математики, так і інших уроків природничо-математичних дисциплін.

Перегляд файлу

АНОТАЦІЯ

Методична розробка «Розвиток творчих компетентностей учнів на уроках математики через використання інтерактивних методик і технологій навчання» розкриває особливості, вимоги, методи та прийоми, результати, ефективність навчання, спрямованого на розвиток особистості учня, дає конкретні рекомендації щодо проведення уроків математики з використанням інтерактивних методик і технологій навчання.

Нова доба принесла нове ставлення до навчання і виховання. Зросли вимоги до людини, а надто до її творчих можливостей, і це з усією очевидністю довело неспроможність авторитарного стилю у навчанні. Тому вивчення цієї теми дуже важливо в наш час.

В роботі розкрито досвід використання інтерактивних методик і технологій навчання на уроках математики. Робота містить практичні додатки інтерактивних завдань, прийомів, які допоможуть викладачу зробити навчання цікавим, різноманітним.

Методична розробка складається з наступних частин:

вступ—визначає необхідність і актуальність застосування інтерактивних методик і технологій навчання;
перша частина—визначає сутність та особливості інноваційної педагогічної діяльності при використанні інтерактивних методик і технологій навчання на уроках математики;
друга частина—розглядає форми та правила організації інтерактивних методик і педагогічних технологій навчання;
третя частина описує структуру урока з застосування інтерактивних методик і технологій навчання;
четверта частина – це плани-конспекти уроків математики, де практично показано застосування інтерактивних методик і технологій навчання;
в наступних розділах зазначається практичне застосування розробки і підведено підсумки теоретичної складової.

Наприкінці розробки надається список використаної літератури.
Стане у пригоді вчителям математики

ЗМІСТ

Вступ

Сутність та особливості інноваційної педагогічної діяльності при використанні інтерактивних методик і технологій навчання.
1. Особливості інноваційної педагогічної діяльності.
2. Методи педагогічного впливу під час формування активності учнів.
Застосування інтерактивних методик і педагогічних технологій навчання на уроках математики.

2.1 Правила організації інтерактивного навчання.

2.2 Форми інтерактивного навчання.

Застосування інтерактивних методик і технологій навчання відповідно до структури уроку.
Плани-конспекти уроків математики з використанням інтерактивних методик і технологій навчання.

Додатки

Практичне застосування розробки

Висновки

Література

Вступ

Те, що я чую, я забуваю.

Те, що я бачу й чую, я трохи пам'ятаю.

Те, що я чую, бачу й обговорюю, я починаю розуміти.

Коли я чую, бачу, обговорюю й роблю я набуваю знань і навичок.

Коли я передаю знання іншим, я стаю майстром.

Набагато важливіше навчити, ніж просто розповісти.

Сучасне життя розвивається бурхливими темпами, тому відбулися вагомі зміни у системі освіти. Викладач, навіть найталановитіший, уже не може бути єдиним джерелом інформації. Традиційна технологія навчання, є насамперед авторитарною педагогікою вимог; навчання дуже слабо пов’язане із внутрішнім життям учня, з його різноманітними запитами і потребами, відсутні умови для прояву індивідуальних здібностей, творчих проявів особистості, віддається перевага репродуктивної діяльності над пошуковою, що не відповідає вимогам часу. Як бачимо, настала необхідність переходу від «передачі знань» до «навчання вчитися», «навчати жити». Сучасному учневі не так треба подати тему, як навчити осмислювати її, а він вже потім шукатиме інформацію, яка допоможе розв’язати проблему. Отож повернути учням інтерес до математики, зробити навчання цікавим, посилити бажання учитися спонукало мене до пошуків. На мою думку, сприяти вирішенню поставлених перед освітою завдань мають інтерактивні методики та технології навчання. Саме цим обумовлюється актуальність представленого досвіду.

Існує велика кількість активних та інтерактивних технологій навчання - проблемна лекція, парадоксальна лекція, евристична бесіда, пошукова лабораторна робота, розв'язання ситуаційних задач, колективно групове навчання, ситуативне моделювання. Вони можуть бути використані на різних етапах уроку: під час первинного оволодіння знаннями, під час закріплення й удосконалення, під час формування вмінь та навичок. Їх можна застосовувати також як фрагмент заняття для досягнення певної мети або ж проводити цілий урок з використанням окремої технології.

Сучасне життя потребує активної творчої особистості. Виховати її можна лише впроваджуючи у педагогічну практику стратегії розвитку критичного мислення. Завдання цієї стратегії полягає у „пробудженні свідомості”, коли молода людина усвідомлює реалії, що оточують її, і шукає шляхи розв'язання проблем. Такий підхід співзвучний концепції особистісно-орієнтованого навчання і нерозривно пов'язаний із застосуванням активних та інтерактивних технологій.

Сучасне життя потребує активної творчої особистості. Виховати її можна лише впроваджуючи у педагогічну практику стратегії критичного мислення.

Новизна досвіду полягає в оригінальному використанні інноваційних методик і технологій (інтерактивного навчання, методу проектів, проблемного навчання, технології колективного взаємонавчання , ІКТ, ігрових технологій) у вивченні математики.

Реалізація інноваційного підходу до навчання учнів дозволяє підняти на якісно новий рівень педагогічний процес, підвищити рівень навчальних досягнень, забезпечує психолого - емоційний комфорт і подальшу соціальну адаптованість учнів, готовність реалізувати особисті якості в індивідуальній чи колективній діяльності, орієнтує на набуття ключових компетентностей : навчальної; культурної; громадянської; соціальної; підприємницької.

Для успішного впровадження технологій розвивального навчання необхідно пам'ятати, що уроки мають захоплювати учнів, пробуджувати в них інтерес до самостійного мислення та дій. Тому дуже важливо на початку заняття створити позитивну психологічну атмосферу, яка сприятиме розвитку особистості. Дітей потрібно вразити, здивувати, зацікавити та інтригувати.

Провідна ідея: впровадження інтерактивних методик і технологій на уроках математики, спрямованих на створення умов співробітництва учнів з метою формування у школярів самоосвітніх компетентностей

Актуальність досвіду:

інтенсифікація та оптимізації навчального процесу;
підвищення ефективності уроку як основної одиниці навчально-виховної діяльності;
активізації навчальної діяльності учнів на уроках математики, підвищення інтересу до предмета;
можливість розвитку навичок самостійної та спільної діяльності;
забезпечення оптимізації соціально - особистісного росту школяра, формування готовності до подолання труднощів навчання та життя, стійкості до стресів і життєвих негараздів;
формування компетентної особистості;
підвищення мотивації навчання.

Сутність та особливості інноваційної педагогічної діяльності при використанні інтерактивних методик і технологій навчання.

1.1. Особливості інноваційної педагогічної діяльності.

Зараз існує чимало визначень педагогічної технології. Поняття «педагогічна технологія» нині має понад триста визначень, залежно від того, як науковці уявляють структуру і складові навчально - виховного процесу.

Технологія ─ грецьке слово за походженням (tehne ─ «мистецтво», «ремесло», «наука», logos ─ «поняття», «вчення») ─ форма реалізації людського інтелекту, сфокусованого на розв’язанні суттєвих проблем буття.

Педагогічна технологія тісно взаємопов’язана з педагогічною діяльністю. У педагогічній діяльності головними діючими особами є викладач і учень. Саме вони на кожному етапі педагогічної діяльності, взаємодіючи один з одним і колективом у цілому, спільно вирішують завдання виховання, навчання і розвитку.

Інновації в педагогіці пов’язані із загальними процесами у суспільстві, а саме глобалізацією, прискоренням темпу життя, комп’ютерізацією, перспективами розвитку людства, національного буття народу. Тому необхідна нова педагогіка, характерною ознакою якої є інноваційність ─ здатність до оновлення, відкритість новому.

Сьогодні все очевиднішим стає те, що традиційна школа, орієнтована на передавання знань, умінь, і навичок, не встигає за темпами їх нарощування. Сучасна школа недостатньо розвиває здібності, необхідні її випускникам для того, щоб самостійно визначитися у світі, бути активними і мобільними суб’єктами на ринку праці, приймати обгрунтовані рішення щодо свого майбутнього. Головними недоліками традиційної системи освіти є небажання дітей вчитися, несформованість ціннісного ставлення до власного розвитку і освіти. Подолання кризи сучасної освіти можливе завдяки інтенсивному реформування її відповідно до вимог часу, у процесі формування принципово нової системи загальної освіти, яка поступово замінюватиме традиційну. Особливістю сучасної системи освіти є співіснування двох стратегій організацій навчання ─ традиційної та інноваційної.

Інноваційне навчання орієнтоване на формування готовності особистості до динамічних змін у соціумі за рахунок розвитку здібностей до творчості, різноманітних форм мислення, а також здатності до співробітництва з іншими людьми. Інноваційне (лат. innovatio ─ оновлення, зміна) навчання ─ зорієнтоване на динамічні зміни в навколишньому світі, це навчальна та освітня діяльність, яка ґрунтується на розвитку різноманітних форм мислення, творчих здібностей, високих соціально адапційних можливостей особистості.

Методи педагогічного впливу під час формування активності учнів.

Підвищення ефективності навчання безпосередньо залежить від доцільності добору і використання різноманітних, найбільш адекватних навчальній темі методів навчання, а також від активізації всього навчального процесу.

Традиційне тлумачення терміну "методи навчання" є таким: це "упорядковані способи взаємопов'язаної діяльності вчителя й учнів, спрямовані на розв'язання навчально-виховних завдань".

На практиці буває важко визначити чіткі межі між різними методами навчання: вони перетинаються, доповнюють один одного, складаються в комплексний "пакет", систему прийомів, за допомогою яких викладач і учні реалізують поставлені цілі.

Вибір методів навчання зумовлений:

цілями навчання;
змістом навчального матеріалу та специфікою предметної області;
темпом та терміном процесу навчання;
стилем навчання та рівнем педагогічної майстерності педагога;
дидактичним та матеріально-технічним забезпеченням процесу навчання;
рівнем підготовки учнів.

Кожен з методів навчання має певні переваги і недоліки. Ефективність їх застосування визначається специфікою конкретного процесу навчання. Універсальних рекомендацій щодо складу і застосування методів навчання не існує. Викладач самостійно приймає рішення про використання того чи іншого методу на основі свого власного досвіду, врахування особливостей учнівської аудиторії з метою максимальної ефективності процесу навчання.

При плануванні конкретних уроків необхідно враховувати, що будь-який метод навчання має тією чи іншою мірою забезпечувати:

активну участь учнів у процесі навчання;
встановлення зворотного зв'язку в системі "викладач-учень";
можливість застосування набутих навичок і знань в реальних життєвих та навчальних ситуаціях;
розвиток цільових навичок поведінки (самостійної творчої діяльності роботи в малих групах);
мотивацію учнів до підвищення ефективності своєї діяльності на заняттях і в реальних ситуаціях;
можливість отримувати знання на груповому та індивідуальному рівнях.

У процесі навчання найбільш доцільне використання, в першу чергу, тих методів, при яких:

в учнів розвивається бажання до творчої, продуктивної праці;
учні прагнуть до активних дій, досягають успіхів і мотивують власну поведінку;
відпрацьовуються моделі поведінки, необхідні для успішної професійної чи підприємницької діяльності.

Цим вимогам найбільш відповідають інтерактивні методи навчання (ІАМН). Слово "інтерактив" (пер. з англійської "intеr" - "взаємний", "асt" - діяти) означає взаємодіяти.

Інтерактивний метод - це спосіб взаємодії через бесіду, діалог. Найбільш ефективні результати при застосуванні ІАМН можна отримати при організації роботи учнів малими групами.

Інтерактивне навчання - це навчання в режимі діалогу, під час якого відбувається взаємодія учасників педагогічного процесу з метою взаєморозуміння, спільного вирішення навчальних завдань, розвитку особистісних якостей учнів.

Суть інтерактивного навчання у тому, що навчальний процес відбувається за умови постійної, активної взаємодії всіх учнів. Це співнавчання, взаємонавчання (колективне, групове, навчання у співпраці), де учень і викладач є рівноправними, рівнозначними суб’єктами навчання, розуміють, що вони роблять, рефлектують із приводу того, що вони знають, вміють і здійснюють. Організація інтерактивного навчання передбачає моделювання життєвих ситуацій, використання рольових ігор, спільне вирішення проблеми на аналізу обставин та відповідної ситуації. Воно ефективно сприяє формуванню навичок і вмінь, виробленню цінностей, створенню атмосфери співробітництва та взаємодії.

2. Застосування інтерактивних методик і педагогічних технологій навчання на уроках математики.

2.1 Правила організації інтерактивного навчання.

Інтерактивні технології базуються на постійній активності взаємодії всіх учасників навчального процесу. Це спів навчання, взаємо навчання, тісна взаємодія в міні-колективі (групи, ланці, команді), коли і учні, і викладач є рівноправними суб'єктами навчання.

Яких правил необхідно дотримуватись при організації інтерактивного навчання на уроках математики?

1. Правило перше. У роботу повинні бути залучені (в тій чи інший мірі) всі учні;

2. Правило друге. Активна участь учнів у роботі має заохочуватися;

3. Правило третє. Учні мають самостійно розробляти та виконувати правила роботи у малих групах;

4. Правило четверте. Учнів під час використання ІАМН не повинно бути більш 30 осіб. Тільки в цьому випадку можлива продуктивна робота у малих групах;

5. Правило п'яте. Навчальна аудиторія повинна бути підготовлена до роботи у великих та малих групах.

Практика показує, що при використанні ІАМН, учні запам'ятовують:

80% того, що висловлювали самі;
90% того, що робили самі.

Поліпшується не тільки запам'ятовування матеріалу, але і його ідентифікація, використання у повсякденному житті. Використання інтерактивних методів навчання в малих групах сприяє розвитку таких особистісних якостей як комунікабельність, співробітництво, уміння відстоювати свою точку зору, йти на компроміси і т.д.

2.2 Форми інтерактивного навчання.

Інтерактивне навчання ─ спеціальна форма організації пізнавальної діяльності, метою якої є створення комфортних умов навчання, за яких кожен учень відчуває свою успішність, інтелектуальну спроможність.

Під час організації та планування інтерактивного навчання викладачу необхідно:

на високому рівні підготувати методичний матеріал (наприклад різноманітні тексти, зразки документів, приклади, ситуації, завдання для груп тощо) ;

навчити дітей виконувати самостійні підготовчі завдання;
старанно спланувати і розробити заняття;
мотивувати учнів до вивчення шляхом добору найцікавіших питань, проблем, виробити критерії оцінки роботи учнів;
знати і досконало володіти різноманітними методами для привернення уваги учнів, налаштування їх на роботу, підтримання дисципліни;
підібрати до уроку такі інтерактивні вправи, які дали б учням відповідь на поставлені питання;
проводити спокійне глибоке обговорення за підсумками інтерактивної вправи, зокрема акцентувати увагу й на іншому матеріалі теми, прямо не порушеному в інтерактивній вправі

На мою думку, необхідно наголосити на активних методах навчання математики:

Метод конкретної ситуації (краще розв’язати одну задачу декількома способами, що сприяє розвитку у учнів критичного мислення, вчить аналізувати, узагальнювати, бачити різні варіанти подолання поставленої проблеми). (Додаток № 1) .

Визначення:

• Вивчення та аналіз реальної чи ви-гаданої, але реалістичної ситуації, події, явища.

Цілі

• Розвиток вмінь вирішення проблем, прийняття рішень;

• Зв'язок теоретичного навчання з виробництвом;

• Аналіз комплексних ситуацій;

• Розвиток міжособистісних відносин

Переваги:

• Реалістичність ситуації» що була розглянута;

• Розвиток навичок самонавчання;

• Інтенсивний процес групової взаємодії;

• Взаємонавчання учнів;

• Синтез різних точок зору;

• Розвиток навичок відбору оптимального варіанту вирішення ситуації;

• Практичне відпрацьовування теоретичних знань;

• Розвиток особистісних навичок.

Обмеження:

• Вимагає витрат часу на підготовку опису ситуації;

• Обмеженість конкретною ситуацією необхідність постійного відновлення;

• Ризик невідповідності/неповної відповідності вимогам навчання і запитам цільової аудиторії

Метод мозкового штурму (привчає учнів давати свої варіанти відповідей).

Визначення:

• Неструктурований процес генеру-вання та відбору інноваційних творчих ідей у групі, що координу-ються педагогом.

Цілі:

• Тренування учнів у вирішенні проблем;

• Розвиток творчого мислення;

• Розвиток навичок спілкування, роботи у малих групах;

• Підвищення зацікавленості учнівської аудиторії

Переваги:

• Високий ступінь активності учнів;

• Продуктивні результати;

• Досвід творчої діяльності;

• Орієнтованість на вирішення проблем;

• Розвиток особистісних навичок учасників;

• Стимулювання нових ідей;

• Невеликий термін

Обмеження:

• Розмір групи має бути не дуже великим чи дуже маленьким (5-7 чоловік);

Процес координування групових дискусій і узагальнення ідей вимагає високої майстерності педагога;

• Різна "якість" результатів навчання, які досягаються при мозковому штурмі

Метод евристичних питань (спонукає учнів аналізувати ).

Обговорення критичного явища

Визначення

Подібний метод з обговоренням

конкретної ситуації з наступними

розходженнями:

• аудиторії повідомляється про яку-небудь критичну ("позаштатну") ситуацію на виробництві у міжособистісних стосунках;

• учні задають педагогу питання, прагнучи одержати додаткову інформацію;

• критична ситуація може бути запропонована самою аудиторією;

• при аналізі й обговоренні допускається більша ступінь свободи в обґрунтуваннях.

Цілі:

• Розвиток вмінь прийняття рішень і усунення проблем у нестандартних (критичних) ситуаціях;

• Розвиток міжособистісних відносин

Переваги:

• Більш конкретний метод в ілюстрації реальних проблем;

• Учні більш активно розкривають послідовність дій, що відбулися;

• Учні асоціюють себе з тим чи іншим учасником певної події;

• Менші витрати на підготовку і проведення у порівнянні з попереднім методом.

Обмеження:

• Вимагає високої активності і тренованості аудиторії в постановці питань;

• Імовірність зайвої емоційності учнів при обговоренні;

• Необхідність чіткого співвідношення розглянутого явища з цілями навчання

"Кошик" (занурення)

Визначення:

• Обговорення конкретної ситуації, при якій учень одержує ряд максимально наближених до реальності матеріалів і проблем, які вимагають вирішення. Можлива організація як групового, так і індивідуального заняття.

Мета:

• Оцінка вхідного рівня й отриманих результатів навчання;

• З'ясування освітніх потреб;

• Розвиток вмінь вирішення проблем;

• Відпрацьовування навичок аналізу ситуації

Переваги:

• Комплексне відпрацьовування різних практичних навичок;

• Ефективний зворотний зв'язок з учнями; Акцент на виконанні, а не тільки на аналізі;

• Закріплення теорії;

• Зміст "кошика" легко пристосовується до потреб учнів;

• Допоміжний засіб для зміни настанов і поглядів.

Обмеження:

• Значні витрати на підготовку кожного заняття; Труднощі в оцінці результатів заняття; Придатний для індивідуального навчання

Форум

Визначення:

• Нетрадиційний спосіб організації процесу обговорення певної теми, при якому виступаючі можуть висловлювати свою позицію без обмеження часу за умови, що їм вдається утримувати увагу аудиторії.

Цілі

• Комунікативний тренінг;

• Творче обговорення проблеми;

• Розвиток вмінь вирішення конфліктів

Переваги:

• Стимулює творче мислення;

• Залучає аудиторію в процес навчання;

• Створює неформальне середовище навчання;

• Реалізує засіб розв'язання конфліктних ситуацій.

Обмеження:

• Вимагає значного часу на підготовку і проведення;

• Ризик одержання результатів, що не сприяють досягненню загальних цілей навчання

Імітація

Визначення:

• Організований педагогом процес відтворення максимально наближених до реальних умов виробничих або міжособистісних ситуацій.

Цілі:

• Професійна діяльність;

• Прийняття рішень;

• Побудова команд;

• Вирішення проблем

Переваги:

• Учень навчається в ситуаційних умовах, максимально наближених до реальних;

• Дієвість навчання;

• Підвищена зацікавленість і висока мотивація учнів;

• Ефективне перенесення теоретичних концепцій у практику.

Обмеження:

• Потребує використання реальних життєвих ситуацій, зрозумілих учням;

• Вимагає значних витрат часу на проведення і підготовку

Діагностика проблеми

Визначення:

• Групове обговорення заданої ситуації з метою встановлення основної проблеми, що лежить у її основі.

Цілі:

• Відпрацьовування навичок вирішення проблем;

• Відпрацювання навичок прийняття рішень

Переваги:

• Проблемно-орієнтовний підхід;

• Глибокий аналіз ситуації;

• Розгляд альтернатив;

• Використання практичного досвіду учнів;

• Структурований виклад варіантів проблем, що лежать в основі розглянутої ситуації.

Обмеження:

• Ризик невідповідності /неповної відповідності/ обраної ситуації практичному досвіду та сфери діяльності учнів;

• Обмеженість практичного застосування отриманих результатів

Семінар

Визначення:

• Зустріч спрямована на обмін результатами дослідження, виконаного проекту; може організовуватися у формі доповідей, обговорень, круглих столів.

Цілі:

• Підсумкове заняття з навчальної теми, дослідження чи проекту;

• Зосередження уваги на нових ідеях, концепціях;

• Вироблення шляхів вирішення проблем

Переваги:

• Узагальнення й аналіз знань з навчальної теми;

• Отримання результатів на основі дослідницької діяльності;

• Обмін досвідом і знаннями;

• Продуктивні ідеї;

• Багатомірний аналіз розглянутих проблем.

Обмеження:

• Високі вимоги до рівня знань учнів;

• Ризик надмірної теоретизації результатів, що ускладнюють їхнє практичне використання

Моделювання

Визначення:

• Наочне зображення різними засобами (макет, графіка, комп'ютерні моделі) системи, структури, пристрою, процесу для аналізу й обговорення.

Цілі:

• Дослідження операцій та процесів за фахом;

• Кількісний аналіз;

• Особистіший розвиток учнів;

• Технічні і технологічні концепції;

• Розробка нових технологій

Переваги:

• Застосовується;

• Надається можливість структурованого обговорення;

• Дозволяється розглядати тему з різних точок зору;

• Стимулюється зацікавленість та увага учнів.

Обмеження:

• Ризик надмірного спрощення моделюючого об'єкту представлення, що призводить до недостатньої глибини аналізу.

• Вимагає спеціальних навичок для розробки

Кооперативний метод (використовується при роботі в групах ).

Групова дискусія

Визначення:

• Спілкування між парами або групами учнів в певній навчальній ситуації. Може бути елементом круглого столу, обговорення конкретної ситуації та інших методів.

Цілі:

• Розкриття теоретичних концепцій;

• Розвиток вмінь вирішення проблем;

• Розвиток вмінь планування, форму-лювання стратегії

Переваги:

• Уточнення і перевірка гіпотез;

• Обмін знаннями і досвідом;

• Залучення у процес навчання;

• Удосконалення навичок комунікації,

Обмеження:

• Різна ступінь залучення учнів у процес обговорення;

• Ризик невідповідності/неповної відповідності ходу дискусії цілям навчання

Точечна групова дискусія

Визначення:

• Організація обговорення в малій групі з метою знаходження ідей з певної теми протягом заданого терміну.

Цілі:

• Закріплення результатів інших занять;

• Встановлення зворотного зв'язку;

• Розвиток вмінь вирішення проблем;

• Розвиток навичок логічного мислення;

• Розвиток навичок взаємодії з іншими людьми

Переваги:

• Високий ступінь залучення учнів у процес навчання;

• Невеликі витрати часу;

• Розвиток творчих здібностей;

• Окремий випадок мозкового штурму;

• Допоміжний засіб для аналізу конкретних ситуацій, прийняття рішень.

Обмеження:

• Придатний тільки для малих груп учнів

Методи роботи учнів у співпраці

Визначення:

• Організація процесу навчання у співпраці малими групами учнів (від 2 до 7 осіб).

Цілі:

• Опрацювання, закріплення, повторення нового матеріалу, вирішення проблем, проектна діяльність, розвиток творчого мислення, комунікативних навичок

Переваги:

• Висока активність і мотивація учнів;

• Високе засвоєння навчальної інформації;

• Розвиток особистісних якостей учнів;

• Розвиток навичок роботи в команді.

Обмеження:

• Потребує попередньої роботи в організації роботи учнів, ретельного підбору учасників малих груп;

• Потребує більшого терміну на проведення, порівняно з пасивними методами навчання.

Метод інциденту (залучення учнів в математичних конкурсах, вікторинах, в олімпіадах, у міжнародній грі «Кенгуру», пробних тестах. Учні вчаться долати стресові ситуації, пасивність).
Ігровий метод.

Рольова гра

Визначення:

• Метод навчання, при якому учні грають визначені ролі в неформальній, але максимально реалістичній манері. Може носити структурований чи спонтанний характер.

Цілі:

• Вироблення стратегії дій у конфліктних і стресових ситуаціях;

• Розвиток цільових поведінкових настанов;

• Розвиток навичок міжособистісного спілкування;

• Розвиток комунікативних навичок;

• Ілюстрація емоційного аспекту діяльності

Переваги:

• Ефективність у відпрацюванні

професійних дій, висвітленні складних конфліктних ситуацій;

• Закріплює засвоєння теоретичних концепцій;

• Прояснює особливості поведінки;

• Розвиває навички оперативного вирішення проблем;

• Навчання в дії;

• Драматичний, ігровий ефект сприяє кращому засвоєння навчального матеріалу;

• Ефективний спосіб зміни настанов і поглядів,

Обмеження:

• Необхідність якісної підготовки "акторів";

• Необхідність ретельного планування сценарію і постановки гри;

• Ризик постановки штучної ситуації;

• Значні витрати часу на підготовку і проведення;

• Необхідність врахування особливостей характеру акторів

Ділова гра

Визначення:

• Одна з форм імітації конкретних ситуацій; передбачає організацію змагання між командами та розподіл ролей між учасниками.

Цілі:

• Відпрацювання функціональних та особистісних навичок.

• Прийняття рішень.

• Побудова команд

Переваги:

• Наочність засобів і результатів навчання (особливо при вивченні сучасних технологій);

• Формування навичок комунікації;

• Відпрацьовування практичних навичок, прийняття рішень;

• Стимулювання творчого мислення;

• Об'єктивна оцінка і зворотній зв'язок; Навчання в дії;

• Демонстрація взаємозв'язків між різними функціями і процесами в організації;

• Розвиток особистісних навичок.

Обмеження:

• Вимагає інтенсивних зусиль по підготовці сценарію і проведенню. Ризик відхилення від цілей навчання

Метод проектів.

Визначення:

• Виявлення, дослідницький пошук та вирішення групою учнів значи¬мої для них проблеми/задачі з ме¬тою одержання реального результату.

Цілі:

• Відпрацьовування навичок вирі-шення проблем;

• Розвиток творчого мислення та особистіших якостей

Переваги:

• Висока залученість учнів у процес навчання;

• Невеликі витрати навчального часу;

• Розвиток творчих здібностей;

• Допоміжний засіб для аналізу обговорюваних конкретних ситуацій» вирішення проблем, прийняття рішень.

Обмеження:

• При частому застосуванні стає механічним, втрачає творчу зацікавленість

3. Застосування інтерактивних методик і технологій навчання відповідно до структури уроку.

Вважаю за необхідне привести орієнтовану структуру уроку із застосуванням інтерактивних методик і технологій.

На одному уроці можна використовувати одну-дві інтерактивні вправи, а не цілий комплекс.

Розпочинаємо урок…

Структура таких уроків складається з п'яти(шести) етапів:

- перевірка домашнього завдання;
- мотивація;
- оголошення теми та очікуваних результатів;
- актуалізація опорних знань ;
- усвідомлення;
- рефлексія.

І. Етап уроку - перевірка домашнього завдання:

Основна умова на цьому етапі ─ виконати перевірку швидко та ефективно. Справитися з цією проблемою дозволяють:

Робота в парах
Вона дуже ефективна на початкових етапах навчання. Організація роботи:

1. Пропоную учням завдання, запитання для невеличкої дискусії, пояснюю його, даю учням 1-2 хв для обдумування можливих відповідей або індивідуальних рішень.

2. Визначаю, хто з учнів висловлюватиметься першим. Щоб привчити дітей до чіткої організації роботи в парах, визначаю час на спільне обговорення. Учні повинні дійти згоди щодо відповіді або рішення.

3. Після того як час буде вичерпано, даю можливість кожній парі представити свої результати роботи.

Гра «Акваріум».

Це рольова гра, в якій беруть участь 2─4 учня, а інші є спостерігачами, що дозволяє одним «проживати» ситуацію, а іншим ─ аналізувати ситуацію збоку. Викликаю кількох учнів, які обговорюють питання домашнього завдання, роблять висновки; вся група уважно стежить, рецензує роботу цієї групи. Викликаю наступну групу, ставлю нове питання. Під час обговорення питань уважно слідкую за роботою учнів у групі, роблю позначки щодо готовності до уроку кожного з них.

Вправа «Знайди помилку».

Варіант 1. Треба знайти у завданні, яке схоже на домашнє , помилки. Можна вказати кількість помилок. Рекомендую у таких завданнях дві-три явні помилки, дві-три типові, одну малопомітну. Виявлення такої помилки свідчить про глибоке знання предмета і розвиває критичне мислення учнів.

Варіант 2. Цей же методичний прийом можна застосувати як командну гру. Кожна команда готує вдома (або на уроці) завдання з помилками з певної теми і пропонує його іншій команді. Для економії часу можна обмінятися текстами, які були заготовлені наперед. Користь подвійна й обопільна - чия команда краще заховає свої помилки і хто більше і швидше знайде.

Вправа«Тести».

Цей методичний прийом останнім часом став надзвичайно популярним та має велику кількість варіацій. Використовую відкриті та закриті тестові завдання. Закриті тести різноманітніші. Одні з них вимагають від учнів лише пригадати вивчений матеріал, інші перевіряють його розуміння і навіть уміння розв’язувати задачі.

Вправа «Розумовий куб»
Для застосування цього прийому використовую пластиковий кубик з дитячого конструктора, ребро якого 10см. На кожній грані кубика записую одне з питань, на які треба дати відповідь. Учень кидає кубик і відповідає на питання, яке йому випало на певній грані. Така робота надає мені можливість створювати ігрові моменти. Застосовую цей прийом під час індивідуального чи фронтального опитування, а також при груповій роботі. Використовую різні підказки для мислення:

опишіть це,
зрівняєте це,
дайте асоціацію цьому,
проаналізуйте це,
застосуєте це,
дайте аргументи за або проти цього.

Приклад використання прийому «Кубик» на уроці геометрії на І курсі під час вивчення теми «Паралельність площин». На гранях кубика в стислому виді написано:

означення паралельних площин,
ознака паралельних площин,
існування площини, паралельної даній площині,
побудова паралельних площин,
властивості паралельних площин,
своя задача
Таким чином, на уроках математики можна перевірити «кубуванням» усі математичні поняття.

Вправа «Математичне доміно»
Усім відома форма роботи. Звичайну картонну картку поділяю на дві частини. В одній записую завдання, а в іншій відповідь на те завдання, яке записане на іншій кістянці доміно. Використовую доміно для індивідуальної, групової і колективної роботи.
Приклад використання доміно під час групової роботи.
Кожна група одержує однакові набори доміно. По команді вчителя учні починають працювати. Перемагає та група, яка першою правильно складе доміно.
Доміно «Тригонометричні формули»

sin 2	tgctg
cos 2	cos² + sin²
cos( + )	1 + tg²
cos(–)	1 – sin²
sin( + )	ctg
sin( –)	1 – cos²
1	1
2 sin·cos	sin·cos + sin·cos
	cos² – sin²
	cos·cos + sin·sin
	cos·cos – sin·sin
	sin·cos–sin·cos
sin²	1 + ctg²
cos²	tg

ІІ. Етап уроку мотивація навчальної діяльності:

Задачі:

Сфокусувати увагу учнів на проблемі;
Викликати інтерес до теми уроку;
Налаштувати учнів на ефективний процес пізнання;
Викликати в учнів особистісну, власну зацікавленість;
Психологічно підготувати учнів до сприйняття теми уроку;
Чітко пов’язати з темою уроку;
Налаштувати учнів на розв’язання певних проблем.

Мета етапу мотивації – сфокусувати увагу учнів на проблемі й викликати інтерес до обговорюваної теми.

Для цього може бути використана нескладна інтерактивна технологія.

Цей елемент уроку має займати не більше 5% часу заняття.

Вправа „ Мікрофон” –

є різновидом загально- групового обговорення , яка надає можливість кожному сказати щось швидко, по черзі, відповідаючи на запитання або висловлюючи свою думку чи позицію, наприклад щодо доцільності вивчення теми.

Вправа „ Незакінчене речення”-

цей прийом часто поєднується з „ Мікрофоном” і дає можливість працювати над формою висловлення власних ідей, порівнювати їх з іншими. Дає присутнім змогу долати стереотипи, вільніше висловлюватися щодо запропонованих тем, відпрацьовувати вміння говорити коротко, але по суті й переконливо.

Наприклад розпочати мотивацію уроку можливо словами:

Сегодня на уроке геометрии мы будем работать вместе, и я рассчитываю на вашу поддержку и помощь. Каждому из вас я хочу пожелать, чтобы вы на этом уроке были:

«У» - улыбчивыми,

«С» - спокойными,

«П» - прогрессивными,

«Е» - естественными,

«Х» - храбрыми

ІІІ. Етап уроку оголошення теми та очікуваних результатів:

Задачі:

забезпечити розуміння учнями змісту їхньої діяльності: чого повинні досягти учні на уроці і чого від них чекає вчитель;
висвітлити результати діяльності на уроці учнів: «Після цього уроку ви зможете …»;
чітко відобразити обсяг і рівень засвоєння знань учнів, що буде забезпечений на уроці; обсяг і рівень розвитку навичок і вмінь, який буде досягнуто після уроку;
розвиток емоційно – ціннісної сфери учня, яка забезпечує формування переконань, характеру, вплив на поведінку;
долучати до визначення очікуваних результатів всіх учнів.

Для того, щоб почати з учнями спільний процес руху до результатів навчання, потрібно:

назвати тему уроку або попросити когось з учнів прочитати її;
якщо назва теми містить нові слова або проблемні питання, звернути на це увагу учнів;
попросити когось з учнів оголосити очікувані результати за записом на дошці, зробленим заздалегідь, пояснити необхідне, якщо йдеться про нові поняття, способи діяльності тощо;
нагадати учням, що наприкінці уроку ви будете перевіряти, наскільки вони досягли таких результатів;
пояснити, як ви будете оцінювати їхні досягнення в балах.

Цей етап уроку має займати не більше 5 % часу заняття.

Вправа «Кросворд»

ІV. Етап уроку актуалізації опорних знань :

Вважаю, що потрібно дати учням достатньо інформації для того, щоб вони могли виконати практичні завдання за короткий час. Тому доцільно використання різних інформаційних технологій та інших технічних засобів навчання.

Вправа«Точка опори», яка може мати досить різноманітні завдання для актуалізації опорних знань учнів з певної теми чи проблеми, яка розглядається. Це можуть бути і запитання, і тестові завдання, і загадки, і кросворди.

Вправа «Базовий аркуш»
Це один із необхідних атрибутів при вивченні нового матеріалу.
На першому ж уроці він вивішується на стенд. У ньому перелічені основні поняття, формулювання, і формули, які зобов'язано повинен знати кожний учень. У старших класах роблю його «двоповерховим». Перша половина - обов'язковий мінімум для всіх. Друга, відділена рисою, містить додаткові питання для претендентів на 10-12 балів і тих, хто готується здавати ЗНО.
Приклад використання прийому на уроці алгебри на ІІ курсі під час вивчення теми «Похідна».

Визначення похідної Похідною функції у точці називається число, до якого прагне відношення при , що прагне до нуля	Правила обчислення похідних. , де с – постійна.
Похідні тригонометричних функцій	Рівняння дотичної

Якою формулою можна доповнити цей перелік?

V. Етап уроку усвідомлення:

Задачі:

учні мають оволодіти інформацією та усвідомити її значення в результаті своєї конструктивної діяльності;
підтримка залученості, зацікавленості, імпульсу учня, отриманого на етапі актуалізації;
підтримка зусиль учня перевірити власне розуміння.

Усвідомлення – етап уроку, протягом якого учні здійснюють пошукову діяльність і в результаті конструюють чи усвідомлюють нове знання. Поєднують нове з тим, що вже знайоме, і, таким чином, розширюють одержані знання. На цьому етапі намагаюся надати учасникам максимум можливостей для самостійної роботи та навчання у співпраці.

Інтерактивна вправа – центральна частина уроку, її метою є засвоєння навчального матеріалу, досягнення результатів уроку.

Інтерактивна частина має займати 50 -60 % часу на уроці. Обов’язковою є така послідовність роботи:

інструктування учнів - вчитель розповідає про мету вправи, правила, послідовність дій і кількість часу на виконання завдань ( 2 -3 хв.)
об’єднання в групи і розподіл ролей.
виконання завдання, при якому вчитель виступає як організатор, помічник, ведучий дискусії, намагаючись надати учням максимум можливостей для самостійної роботи і навчання у співпраці один з одним ( 5 -15 хв.)
презентація результатів виконання вправи (3-5хв.).
рефлексія результатів учнями: усвідомлення отриманих результатів, що досягається шляхом їх колективного обговорення або допомогою інших прийомів (5 -15хв.)

З метою усвідомлення і осмислення знань застосовую прийом «Концептуальна таблиця»
Приклад використання прийому «Концептуальна таблиця» на уроці алгебри під час вивчення теми «Функції»
Пропоную учням заповнити таблицю, працюючи в групах. Потім провести обговорення й порівняння результатів.

Вид функції	Область визначення	Область значень	Зростання спадання	Парність	Нулі функції
y = kx +b
y = ax²+bx+c

Вправа „ Мозковий штурм”-

інтерактивна технологія колективного обговорення, що використовується для вироблення кількох вирішень конкретної проблеми. Спонукає учнів проявити уяву та творчість , дає можливість їм вільно висловлювати свої думки. Застосовую при доведені теорем шляхом «штурму», який організовую за такими етапами:

• Усі учасники пропонують ідеї щодо розв'язання порушеної проблеми.

• Ідеї записуються на дошці.

• Якщо група вважає кількість поданих ідей достатньою, запис їх припиняється.

• Після того як майже всі ідеї зібрані, вони групуються, аналізуються і відбираються.

• Вибираються ті, що можуть допомогти розв'язати порушену проблему.

Під час проведення «мозкового штурму» дотримуюся таких правил:

• збираю якомога більше ідей щодо розв'язання завдання або проблеми;

• змушую працювати уяву учнів, не відкидаючи жодної ідеї;

• подаю кілька своїх ідей або розвиваю ідеї інших;

• не обговорюю і не критикую ідеї інших.

Вправи «Спроба і помилка»-

дозволяє учням дійти правильного висновку, коли я лише направляю їх думки та припущення у вірному напрямку(результатом є алгоритм розв’язання ).

„ Навчаючи – учусь”-

вправа використовується при вивченні блоку інформації або при узагальненні та повторенні вивченого. Він дає можливість учням узяти участь у передачі своїх знань однокласникам. Використання цього методу дає загальну картину понять і фактів, що їх необхідно вивчити на уроці, а також викликає певні запитання та підвищує інтерес до навчання.

«Шпаргалки»-

учням пропонується прочитати текст. Необхідно передати його зміст з допомогою малюнків, умовних позначень або схем, тобто скласти опорну схему.Ці шпаргалки (підписані) віддаються вчителю. За бажанням учні підходять до вчителя і витягають шпаргалку. За цією шпаргалкою потрібно відтворити текст. Відзначаються найкращі шпаргалки та доповідачі.

«Шерлок Холмс»-

учням пропонується скласти якнайбільше запитань до вивченої теми, не користуючись самим текстом. Питання мають охопити весь матеріал і врахувати найменші дрібниці. Визначається найдовший список питань. Учні дають відповіді на них.

«Тести»-

На кожному уроці можна використовувати тести оперативного контролю. Невеликі за розмірами (5-8 запитань), вони можуть здійснюватись у вигляді математичного диктанту, у цьому випадку перелік відповідей на запитання записаний на дошці (у закритому тесті). Краще використовувати два варіанти запитань. Варіанти відповідей, як для кожного варіанта окремо, так і один перелік відповідей для обох варіантів. Такі тести мають навчальний характер, тому перевіряти їх слід одразу ж після виконання. Учитель вибірково перевіряє роботи окремих учнів, усі інші тести обробляються учнями з допомогою взаємоперевірки. Учитель оголошує результати й аналізує помилки.Учні з високим рівнем знань можуть мати додаткові творчі завдання – скласти самостійно тести до вивченої теми.

«Маркувальна таблиця».
З метою дослідження фактів, доказів, формування вміння висловлювати свої пропозиції, думки, ідеї, а також з метою виховання поваги до думки одногрупників застосовую такий прийом як «Маркувальна таблиця».
Аналізувати учні можуть по декільком напрямкам: “це я вже знаю”, “це я чув”, “це не знаю”. Інший приклад: “це я розумію й поясню іншому”, “це я розумію, але пояснити не зможу”, “це я не розумію”.

Підсумкова таблиця має вигляд:
Приклад використання прийому «Маркувальна таблиця» на уроці алгебри на ІІІ курсі по темі «Статистика».
У ході підготовки до уроку ви збирали інформацію, користувалися різними термінами. Зараз вам буде запропонована таблиця. Укажіть, які слова в ній відносяться до статистичних термінів. Для цього використовуйте позначки «+», «-», «?», «v», які будуть означати відповідно:
«+» - да
«-» - немає
«?» - сумніваюся
«v» - не знаю, чи ставиться це слово до статистичної інформації:

№	Чи статистичний це термін?	Відповідь (+,-,?,v)
	Розмах Конкуренція Співробітництво Мода Середнє арифметичне Частота Прибуток Кредит Інтервальний ряд Репрезентативність

Для більш швидкого підрахунку даних заповните, будь ласка, таблицю частот знаків:

Таблиця частот
+	-	?	v

Вправа «Інтелектуальна провокація».
Приступаючи до вивчення теми, я передбачаю «тонкі» місця і не словами попереджаю про небезпеку зробити помилку, а намагаюсь створити ситуацію, в якій учень змушений бути особливо уважним, а якщо все ж таки допустить помилку, то зможе виправити її правильно виконавши подібне завдання.
Цей прийом замінює опитування. Кожна така «провокація» повинна бути продуманою (не просто набір запитань типу «Що називається...?», «Як розв’язується …?»). Цей різновид евристичної бесіди набагато більш ефективний, ніж традиційна робота над помилками, хоча й не заміняє її. Цей метод передбачає можливу «зустріч із помилкою» під контролем викладача.

Приклад використання вправи на уроці алгебри на ІІ курсі під час вивчення теми «Похідна»
При обчисленні похідної функції y = sin²x учні вибирають із двох запропонованих відповідей
y^/= 2 sinx замість y^/= sin 2x, не враховуючи, що задана функція є складної, тому y^/= 2sin x (sin x)^/= 2sin x cos x = sin2x.

Вправа «Наведи порядок».

Роздаю учням розрізні прямокутники, в яких переплутані формули, розв’язки, тощо і пропоную навести порядок. Приклад використання прийому на уроці алгебри під час вивчення теми «Тригонометричні рівняння»

2n			n
cosα = 1	cosα = 0	sinα = 1	sinα = 0	tgα = 1
sinα = -1	cosα = -1	tgα = -1	сtgα = -1	sinα = 2
	 + 2n			нет

Вправа «Куточки»
Приклад використання прийому на уроці алгебри на ІІ курсі під час вивчення теми «Похідна»
В клетках таблицы в беспорядке записаны функции и их производные. Для каждой функции найдите производную и запишите соответствие номеров клеток. Например: 1-9.

x⁵		x		2x		1		2
	1		2		3		4		5
x^-3				sin x		5x⁴		-3x ^-4
	6		7		8		9		10
		-3		- sin x		-		ax
	11		12		13		14		15
a		cos x				0		12x ^-5
	16		17		18		19		20

VІ. Етап уроку рефлексія.

На цьому етапі прояснюємо зміст проробленого; підбиваємо підсумок засвоєння знань; встановлюємо зв’язок між тим, що відомо і тим, що повинно вдосконалюватися в майбутньому.

Одним із важливих видів діяльності, вважаю проблемне навчання, яке активізує пізнавальну роботу учнів, що веде до ґрунтовного засвоєння і закріплення наукових знань, розвиває творче мислення, здатність до самостійного вирішення поставленого завдання.

Віддаю перевагу тим прийомам і методам, що дозволяють виробити в учнів свої аргументи або думки, усвідомити отримані результати, узагальнити вивчений матеріал. Часто ─ це робота в парах або групах; колективне обговорення; дискусії, письмовий звіт.

Задачі:

Пояснити зміст опрацьованого;
Порівняти реальні результати з очікуваними;
Проаналізувати, чому сталося так чи інакше;
Зробити висновки;
Закріпити чи відкоригувати засвоєння;
Намітити нові теми для обміркування;
Установити зв’язок між відомим і тим ,що потрібно засвоїти, чого навчитись у майбутньому;
Скласти план подальших дій.

Рефлексія – фаза уроку, протягом якої учні роблять огляд ідей, що були відкриті ними, значення яких вони усвідомили; учні запитують, інтерпретують, застосовують, сперечаються, змінюють та розширюють одержані знання. Підсумки є найважливішою частиною інтерактивного уроку. Підсумковий етап уроку містить такі під етапи:

Установлення фактів ( що сталося?):

2.Аналіз причин ( чому це сталося?):

3.Планування дій ( що нам робити далі?):

Для підсумків уроку та оцінювання його результатів у балах доцільно залишати до 20 % часу.

Під рефлексією психологи розуміють самоаналіз, розмірковування над тим, що людина знає, думає, міркує. На цій стадії учень перетворює нові знання на власні, оскільки висловлює їх своїми словами. В кінці уроку повертаємося до записів на дошці, зроблених на початку уроку, уточнюємо, що зі сказаного підтвердилося, чи досягли поставленої перед собою мети, чому навчилися.

Вправа«Прес»-

Учні висловлюють свої думки стосовно уроку за алгоритмом.

Ми вивчили …

Ми навчилися …

Нас зацікавило …

Отже, …

Обов’язково звертаю увагу на невербальні комунікації – стан душі кожного учня, з яким закінчують урок. Намагаюся зняти напругу, а також поставити нову мету для освітньої діяльності, причому учні самі беруть на себе зобов’язання щодо подальших дій. Для кращої організації навчальної діяльності на уроці рекомендую дати відповіді на запитання: що сподобалося на уроці?, що не сподобалося?, чи задоволені ви собою?, поставте оцінку собі та дайте собі завдання. Якщо треба провести рефлексію емоційного стану використовую або кольорові картки настрою , або « смайлики».

Вдало вписується у структуру уроку метод проектів (дослідницьких, ігрових, інформаційних,практично орієнтованих, групових,особистих), які я використовую у вигляді випереджувальних завдань, для створення проблемних ситуацій у ході вивчення нового матеріалу та як підсумок на етапі закріплення, систематизації і узагальнення знань.

Метод проектування допомагає учневі бути не пасивним реципієнтом готових знань, а суб'єктом навчання, який активно включається у спільну діяльність, відчуває себе рівноправним учасником діалогу, співтворцем. Це саме той вид діяльності, який наочно демонструє практичне застосування набутих знань (Додаток №2).

4. Плани-конспекти уроку уроків математики з використанням інтерактивних методик і технологій навчання.

Предмет «Алгебра та початки аналізу».

Урок з теми «Показникові рівняння».

Мета:

навчальна:

формування поняття показникового рівняння;
формування вміння розв’язувати показникові рівняння.

розвивальна:

розвиток мислення учнів, розвиток математичної мови;
розвиток мотиваційної сфери особистості;
розвиток дослідницьких здібностей.

виховна:

виховання наполегливості при розв’язуванні проблеми;
здійснення формування відношень співпраці між учнями при розв’язуванні проблеми.

Тип уроку: урок вивчення нового матеріалу.

Методи: пояснювально-іллюстративний, частково-пошуковий, дослідницький.

Форми пізнавальної діяльності учнів: фронтальна, індивідуальна.

Структура уроку:

Організаційний етап.
Актуалізація опорних знань.
Вивчення нових знань та способів діяльності.
Закріплення нового матеріалу.
Підведення підсумків уроку.
Домашнє завдання.
Рефлексія.

Хід уроку

I етап. Добрий день. Сідайте.

II етап. Задання для усного обміркування (записані на дошці): Як називаються вирази: . Які ще два поняття пов’язані з цими виразами?

III етап. Оголошується тема уроку та мета уроку:

Дізнатися які рівняння називаються показниковими.
Навчитися розв’язувати показникові рівняння.

Учні записують тему уроку.

Розкривається дошка, на якій записані рівняння:

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

Учням пропонується наступне завдання: усно об’єднати ці рівняння в групи та пояснити за якою ознакою було проведено розподіл.

Учні: Рівняння (1) і (10) можна об’єднати в одну групу, так як це ірраціональні рівняння. Рівняння (2) і (5) – квадратні. Рівняння (3), (4), (6), (8), (9) – мають невідому в показнику степені, тому їх можна також об’єднати.

Вчитель: Правильно. Ви, мабуть, вже здогадались, як називаються рівняння, які входять в останню групу.

Учні: Показникові рівняння.

Вчитель: Спробуйте дати означення показниковим рівнянням (Зауваження: раніше з учнями можна згадати означення ірраціональних рівнянь, а далі за аналогією дати означення показниковим рівнянням).

Учні: Показникові рівняння – це рівняння, у яких невідоме знаходиться в показнику степені.

Вчитель: Запишіть з дошки в зошит тільки показникові рівняння. Я підкреслю показникові рівняння.

Далі учням пропонується невеликий об’єм теоретичного матеріалу.

Розглянемо рівняння наступного виду:

, , , .

Рівняння такого виду називаються найпростішими показниковими рівняннями. Запишіть це в зошит. Такі рівняння розв’язуються за допомогою властивостей степеня:

Степені з додатною основою, а>0, а1 рівні тоді і тільки тоді, коли рівні їх показники.

Подивіться на рівняння, які ви виписали. Які з них є найпростішими рівняннями?

Учні: Рівняння (3) 6 ^х = 36.

Вчитель: Вірно. Давайте його розв’яжемо.

Вчитель записує розв’язання показникового рівняння на дошці, учні – в зошиті.

Вчитель: Подивіться на рівняння, які залишилися. Чи є вони найпростішими? Якщо «ні», то як їх розв’язати?

Учні: Ні.

Вчитель: І так, у нас проблема: Як розв’язати інші показникові рівняння? Ваша думка?

Виникає припущення (гіпотеза): такі рівняння можна шляхом перетворення привести до виду , яке є вже найпростішим, і яке ми вже вміємо розв’язувати. (Зауваження: ця гіпотеза може виникнути при розв’язанні рівняння). Далі розв’язуються всі інші рівняння.

Підсумок: розв’язок будь-якого показникового рівняння можна звести до розв’язання найпростішого показникового рівняння.

IV етап. Пропонується розв’язати рівняння ( на дошці умова).

Далі пропонується розв’язати подібне рівняння самостійно, попередньо пояснивши учням спосіб його розв’язання.

Через п’ять хвилин викладач просить одного з учнів назвати відповідь, інші учні перевіряють правильність своєї відповіді.

V етап. Підсумок уроку проводиться низкою запитань:

- Які рівняння ми сьогодні вчилися розв’язувати?

- Які види рівнянь ви ще знаєте?

- Яка основна ідея використовується при розв’язанні любого показникового рівняння?

VI етап. Учні записують домашнє завданя, викладач коментує.

VII етап. Викладач: згадайте, чи ви все сьогодні зрозуміли на уроці і чому?

Що було не зрозуміло?

На дані запитання можна поговорити з учнями.

Предмет «Алгебра та початки аналізу».

Урок з теми «Показникові нерівності ».

Мета:

навчальна:

формування поняття показникової нерівності;
формування вміння розв’язування показникових нерівностей.

розвивальна:

розвиток мислення учнів;
розвиток пізнавального інтересу, допитливості ;
розвиток вмінь навчально-пізнавальної діяльності;
розвиток вільної сфери особистості.

виховна:

виховання наполегливості, організованості, відповідальності;
здійснення трудового виховання учнів.

Тип уроку: урок вивчення нового матеріалу.

Тривалість заняття – два уроки.

Обладнання: модуль «показникові нерівності», самостійна робота до модулю.

Методи: продуктивний, частково0пошуковий.

Форми пізнавальної діяльності учнів: індивідуальна, групова.

Структура уроку:

етап. Організаційний етап.
етап. Вивчення нових знань і способів діяльності.
етап. Домашнє завдання.
етап. Підведення підсумків уроку.

Хід уроку

1 етап. Учням повідомляється, що сьогодні вони будуть самостійно вивчати тему «Показникові нерівності». При виникненні питань учні можуть звертатися за допомогою до вчителя. На вивчення даної теми відводиться урок і п'ятнадцять хвилин наступного уроку. Наприкінці наступного уроку необхідно буде написати самостійну роботу з вивченої теми, розраховану на двадцять хвилин.

2 етап. Учням видається модуль «Показникові нерівності» (Додаток 3), за яким вони починають працювати.

3 етап. На другому уроці (за двадцять п’ять хвилин до дзвоника) учням надається самостійна робота.

4етап. Домашнє завдання (умова на дошці). Додатково: розв’язати нерівність .

етап. Підсумки уроку підводяться низкою запитань: Які нерівності ви навчилися сьогодні розв’язувати? Які є способи розв’язування показникових нерівностей? Чи важко було вивчати дану тему самостійно?

Додатки

Додаток №1. Метод конкретної ситуації.

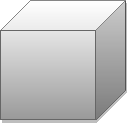
Геометрія, ІІІ курс. Задача. Площина, яка проведена через середини трьох ребер куба, відтинає від нього частину. Знайдіть відношення об’єму відтятої частини до об’єму даного куба.

Розв’язання задачі слід розглянути двома способами: в першому можна піти традиційним шляхом, обчислюючи об’єм піраміди, в основі якої лежить рівносторонній трикутник. Другий спосіб ─ необхідно здогадатися перевернути піраміду на бічну грань, і тоді розв’язання буде значно раціональнішим, так як об’єм піраміди знайдемо таким чином:

V= =.

Додаток №2. Проект «Ремонт Вашої кімнати» .

Тема. Площі фігур.

Мета проекту. Навчальна: формувати вміння застосовувати отримані знання в нестандартних задачах.

Розвиваюча: сприяти розвитку логічних операцій .

Виховна: підтримувати інтерес до предмета, формувати вміння працювати в колективі.

Завдання.

1. Ознайомитись із розв’язуванням поставлених задач для кожної з груп. Скласти та визначити обсяг фінансових ресурсів для ремонту стін та підлоги.

2. Охарактеризувати діяльність кожної групи, оцінити їхні кошториси необхідних будівельних матеріалів для ремонту дитячої кімнати.

3. Зробити висновки.

Підготовча робота.

Вибір теми і мети проекту, визначення кількості учасників проекту, складу груп (три бригади, що представлятимуть такі будівельні фірми: «Майстри», «Світ кераміки», «Будуємо дім»). Відповідно, «Майстри» ─ проводитимуть ремонт, «Світ кераміки» ─ будівельні суміші, «Будуємо дім» ─ матеріали з дерева.

Планування роботи.

Визначення джерел інформації(що необхідно знати, щоб розв’язати завдання ), планування способів збору інформації, планування кінцевого продукту : газета, презентація, Текстовий документ, кошторис ;розподіл обов’язків серед членів бригади.

Ролі

Бухгалтер ─ проводить розрахунки і складає кошторис проекту.
Дизайнер ─ робить ескізи , підбирає матеріал для ремонту.
Постачальник ─ визначає необхідну кількість обраного матеріалу.
Менеджер ─ зачитує інструкції, презентує проект групи і його вартість з обґрунтуванням.
Керуючий ─ слідкує, щоб кожен учасник групи приймав активну участь в розробці проекту.

Дослідницька діяльність

Ознайомитися з матеріали , які пропонують найбільші магазини регіону. Обчислити площі поверхонь, на яких необхідно провести ремонтні роботи. Наприклад, дитяча кімната може мати таку форму :

↓ вікно (2x2 м) 10 м


	*6 м*

8 м

4 м ↑(двері 2×1 м)

Висота стін h= 2,75 м, враховуючи розміри вікна, та дверей

Результати.

Формування висновків : Оформлення результату .

Представлення готового продукту.

Група голосує за найкращий проект, враховуючи використання усіх видів матеріалу, правильне обчислення площі кімнати та зіставлення кошторису. В проекті потрібно правильно зробити висновки щодо економності та доступності кошторису.

Додаток 3. Модуль з теми «Показникові нерівності »

«Тот, кто учится самостоятельно, преуспевает

в семь раз больше, чем тот, которому все объяснили».

(Артур Гитерман, немецкий поэт)

Тема: Показникові нерівності.

Мета:

1. Дізнатися, що таке показникові нерівності.

2. Вивчити основні методи розв’язання показникових нерівностей.

3. Навчитися розв’язувати показникові нерівності

Учбовий елемент №1.

Записати тему в зошит.
Згадати, що називається показниковим рівнянням. Написати в зошиті за аналогією означення показникової нерівності.
Прочитайте теорію (див. нижче). Записати в зошит інформацію, яку вважаєте за необхідну.

Теорія

Розглянемо розв’язання показникових нерівностей виду , де b – деяке раціональне число.

Якщо , то показникові функція монотонно зростає і визначена для всіх х. Для зростаючої функції більшому значенню функції відповідає більше значення аргументу. Тоді нерівність рівносильна нерівності .

Якщо , то показникова функція монотонно спадає і визначена для всіх х. Для спадаючої функції більшому значенню функції відповідає менше значення аргументу. Тоді нерівність рівносильна нерівності .

Розгляньте наведені нижче приклади розв’язання показникових нерівностей виду .

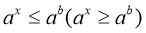Приклад. Розв’яжемо нерівність .

Напишемо нерівність у вигляді . Так як , то показникова функція зростає. Тому дана нерівність рівносильна нерівності . Відповідь : .

Приклад 2. Розв’яжемо нерівність .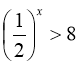

Напишемо нерівність у вигляді .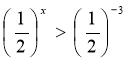

Так як , то показникова функція 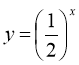спадає. Звідси дана нерівність рівносильна нерівності . Відповідь : .

Розв’язати нерівності:

; .

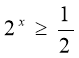Дайте повне обґрунтовування розв’язуванню нерівностей (див. приклади). Проконтролюйте правильність розв’язання нерівностей, звіривши отриманні відповіді з відповідями сусіда по парті.

Учбовий елемент №2.

1.Прочитайте теорію (див. нижче). Записати в зошит інформацію.

Теорія .

Розглянемо розв’язання показникових нерівностей виду ,

де і деякі функції залежні від .

Частковим випадком нерівностей є нерівності виду, де – деяке дійсне число.

Для розв’язання нерівностей розглянутих видів використовується властивість зростання або спадання показникової функції.

Розв’яжемо нерівність (*).

Розглянемо показникові функцію і значення показникової функції при t₁=f(x) та при t₂=g(x). Перепишемо дану нерівність (*) у вигляді (**).

Якщо , то функція зростає. Тоді нерівність (**) рівносильна нерівності . А дана нерівність (*) рівносильна нерівності .

Якщо , то функція спадає. Тоді нерівність (**) рівносильна нерівності . А дана нерівність (*) - нерівності .

Розглянемо наведені нижче приклади розв’язання показникових нерівностей виду .

Приклад 1. Розв’язати нерівність .

Запишемо нерівність у вигляді . Показникові функція зростає . Тому дана нерівність рівносильна нерівності . Звідси . Розв’язавши квадратну нерівність, отримаємо . Відповідь: .

Приклад 2. Розв’язати нерівність .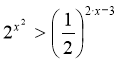

Запишемо нерівність у вигляді . Показникова функція зростає . Тому дана нерівність рівносильна нерівності

, звідси . Розв’язавши квадратну нерівність, отримаємо або .

Відповідь: .

2.Розв’язати нерівності. Дайте повне обґрунтовування розв’язуванню наступних нерівностей.

;

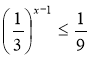Проконтролюйте правильність розв’язання нерівностей, звіривши отриманні відповіді з відповідями сусіда по парті.

Учбовий елемент №3.

Розв’язання деяких показникових нерівностей зводиться до розв’язання квадратних нерівностей. Розглянемо приклад такої показникової нерівності.

Приклад . Розв’яжемо нерівність .

Нехай , тоді отримаємо квадратну нерівність .

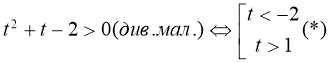
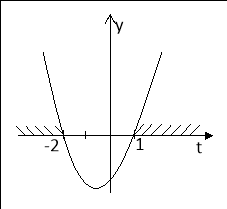
Так як , то маємо сукупність

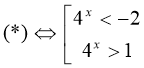
Перша нерівність не має розв’язків, так як при всіх . Другу нерівність можна записати у вигляді , звідки .

Відповідь:

Розв’язати нерівність 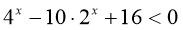. Проконтролюйте правильність розв’язання самостійно.

Виконайте самостійну роботу в зошитах. Не забувайте обґрунтувати свої рішення.

Самостійна робота

Варіант №1.

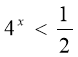
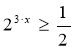
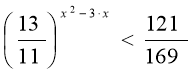
Варіант №2.

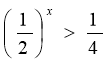
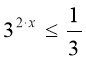
Оцінити свою роботу на уроці за 10 бальною шкалою (відмітьте свою точку на шкалі)

Практичне застосування розробки

На уроках, де використовуються інтерактивні методики і технології навчання, діти почувають себе впевнено, вільно висловлюють свої думки і спокійно сприймають зауваження, адже вони є активними учасниками навчального процесу.

В атмосфері довіри та взаємодопомоги легко робити відкриття, усвідомлювати важливість здобутих знань.

Саме за таких умов можливе виховання особистості, підготовленої до майбутнього, у якому необхідно розв'язувати проблеми та приймати конкретні рішення.

На мою думку, за умов інтерактивного навчання учень може навчатися робити свідомий вибір серед широкого спектра альтернатив і брати на себе відповідальність приймати самостійні рішення, щодо розв'язку задач та вправ. Важливо, що кожен може це робити свідомо й грамотно. У результаті застосування інтерактивних технологій створюються сприятливі можливості й для духовного розвитку особистості, а також ефективному процесу соціалізації. Слід зазначити, що інтерактивне навчання дозволяє різко збільшити процес засвоєння матеріалу, оскільки впливає не лише на свідомість учня, а й на його почуття, волю (дії, практику). Результати цих досліджень можна відобразити в схемі, що отримала назву „ Піраміда навчання".

Інтерактивні методи навчання дають можливість активізувати мислення учнів, залучати учнів до плідної бесіди, мотивувати навчання, показувати різні точки зору, допомагає ставити свої запитання та формувати власну думку.

Інтерактивне навчання дозволяє розв'язати одразу кілька завдань: розвиває комунікативні вміння й навички, допомагає встановленню емоційних контактів між учасниками процесу, забезпечує виховне завдання, оскільки змушує працювати в команді, прислухатися до думки кожного. Використання інтерактивного навчання знімає нервове напруження, дає можливість змінювати форми діяльності, переключати увагу на основні питання.

Готуючись до кожного уроку, думаю над тим, щоб був побудований методично вірно, намагаюся, щоб урок на урок не був схожий. На своїх уроках намагаюся стимулювати творчий пошук, використовую різні методи і форми роботи, прищеплюю учням навички самостійної роботи з книгами; розвиваю навички роботи в групі, вміння слухати товаришів та висвітлювати свою думку; привчаю до дослідження, пошуку, спостережливості.

Методичну розробку можна використовувати для підготовки уроків з використанням інтерактивних методик і технологій навчання, як математики, так і інших уроків природничо-математичних дисциплін.

Висновки

Педагогічний професіоналізм — уміння викладача мислити та діяти професійно. Охоплює набір професійних властивостей та якостей особистості педагога, що відповідають вимогам учительської професії; володіння необхідними засобами, що забезпечують не тільки педагогічний вплив на вихованця, але і взаємодію, співробітництво та співтворчість з ним. Для активного співробітництва з вихованцями викладачу необхідна мобілізація інтелекту, волі, моральних зусиль, організаторського хисту та вміле оперування засобами формування моральних, інтелектуальних та духовних засад у школярів.

Він повинен володіти широким арсеналом інтелектуальних, моральних та духовних засобів, що забезпечують педагогічний вплив на учня. До інтелектуальних засобів належать кмітливість, професійне спрямування сприйняття, пам'яті, мислення, уяви, прояв та розвиток творчих здібностей учня. До моральних — любов до дітей, віра в їх можливості та здібності, педагогічна справедливість, вимогливість, повага до вихованця — все, що складає основу професійної етики вчителя. Духовні засоби — основа його загальної та педагогічної культури.

Розвиток творчого потенціалу людини трактується як основне завдання навчального закладу. Для реалізації його потрібно насамперед розглядати учня не як суму зовнішніх впливів, а як цілісну, активну, діяльну особистість. Учень ─ не об'єкт, а насамперед творець свого власного „Я”.

Крізь призму діяльності учня необхідно переосмислити саму структуру навчально-виховного процесу. Такий навчально-виховний процес передбачає певну переорієнтацію функцій вчителя. Різко зменшується питома вага його виконавчої діяльності на уроці, а також зростає функція організаційна.

Учитель повинен стати творцем своєї діяльності й сам відповідати за її результати. Така форма роботи можлива в разі співпраці учителя й учнів. Функції вчителя визначаються як зовнішні щодо системи „учень - предмет”. Учитель є організатором і співучасником навчально-виховного процесу. Проте це не означає, що в системі навчально-виховного процесу роль вчителя зменшується. Навпаки, чим більше вчитель виявляє себе, тим вагомішим буде результат навчально-виховного процесу. Суть проблеми полягає в тому, куди учитель спрямує свої зусилля - на чітку організацію діяльності учня чи на ту роботу, яку повинен виконати учень. Це принципове питання, тому функції учня і вчителя повинні бути чітко розмежовані. У кожного з них є своя діяльність - учень навчається, учитель керує його діяльністю.

Психологічний портрет викладача, налаштованого на особистісно-орієнтоване спілкування: відкритість, доступність, створення для дітей можливостей висловлювати свої думки і почуття; справедливість, довіра до дітей, визнання їх неповторності, гідності; зацікавленість життям учнів, увага до їхніх проблем; емпатійне розуміння (здатність бачити поведінку учня його ж очима, відчувати його внутрішній світ); готовність завжди допомогти учням.

Лише правильний стиль поведінки викладача викликає свободу, довіру, відсутність страху, відкритість, устремління до доброзичливого ставлення у групі.

Для успішної участі у сучасному суспільному житті особистість повинна володіти певними прийомами математичної діяльності і навичками їх застосувань до розв’язування практичних задач. Значні вимоги до математичної освіти у ров’язанні практичних задач ставлять сучасний ринок праці, отримання якісної професійної освіти, продовження освіти на наступних етапах. Тому одним із головних завдань навчання математики є забезпечення умов для досягнення кожним учнем математичної компетентності.е5е55434у

У підсумку, можна зробити висновок :

Позитивні аспекти інтерактивної моделі:
1) розширюються пізнавальні можливості учня.
2) підвищує рівень засвоєння знань.
3) без зусиль можливо проконтролювати рівень засвоєння знань учнями
4) кожен (і викладач, і учень) має змогу розкритися як організатор, консультант.
5) партнерство між викладачем і учнями та в учнівському колективі.

Негативні аспекти інтерактивної моделі:
1) на вивчення певної інформації потрібен значний час.
2) необхідний інший підхід в оцінюванні.
3) мало досвіду такого способу організації навчання.
4) нестача методичних розробок уроків з використанням інтерактивних методів і технологій навчання.

Література

Закон України «Про освіту».
Інтерактивні технології навчання: теорія, досвід: Методичний посібник. / Авт.-уклад. О. Пометун, Л. Пироженко. - 2007.
Іванішена С. Форми та методи інтерактивного навчання . - 2006. - № 3. - C. 9-11
Інтерактивні вправи та ігри. – Харків: ВГ «Основа», 2010 (Серія «Адміністратору школи»
Сиротинко Г.О. Сучасний урок: інтерактивні технології. – Харків: ВГ «Основа», 2003
Вердіна С.В., Панченко А.Г. Секрети педагогічної майстерності. – Харків: ВГ «Основа», 2008
Ворожейкіна О. М. 100 цікавих ідей для проведення уроку. ─ Х. : Вид. група «Основа», 2012. ─ 3-тє вид. ─ 255 с.
Ігрові технології навчання на уроках математики // Упоряд. Коць Т. Г. ─ Тернопіль- Харків: Видав. «Ранок», 2012.─ 176 с.
Садкіна В. І. 101 цікава педагогічна ідея. Як зробити урок.─Х.: Вид. група «Основа», 2008.-88 с.
Пометун О. Сучасний урок інтерактивні технології – Київ: А.С.К., 2005
Дичківська І. М. Інноваційні педагогічні технології: Навчальний посібник. ─ К.: Академ.видав., 2004. ─ 352 с.
Суворова Н. Интерактивное обучение: новые подходы // Инновации в образовании. – 2001. - №5.
Сухарева Л.С. Дидактичні ігри на уроках математики. – Харків: «Тріада +», 2006
Пометун О.І., Пироженко Л.В. Сучасний урок. Інтерактивні технології навчання. - К.: А.С.К., 2004. ─ 192 с.
Сучасний урок. Інтерактивні технології навчання: Науково-методичний посібник / О.І.Пометун, Л.В. Пироженко; За ред. О.І. Пометун. - К.: А.С.К., 2003.
Новицька Л. Б. Інтерактивні методи навчання математики. Практичний посібник // Математика в школах України. ─ 2008. ─ с. 5-9.
Нісімчук А.С., Падалка О.С., Шпак О.Т. Сучасні педагогічні технології. К, 2000. ─ 176 с.
Метод проектів на уроках математики // Упоряд. Л. К. Гладій ─ Х.: Видав. «Ранок», 2012.─ 160 с.
Крамаренко С.Г. Інтерактивні техніки навчання як засіб розвитку творчого потенціалу учнів // Відкритий урок. – 2002. - №5-6.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Ющенко Любов Федорівна

Пов’язані теми

Математика, Методичні рекомендації

Додано

29 січня 2020

Переглядів

20450

Оцінка розробки

Відгуки відсутні