Методичні матеріали для практичного заняття "Елементи теорії ймовірності"
ЕЛЕМЕНТИ ТЕОРІЇ ЙМОВІРНОСТЕЙ
Практичне заняття
Розв’язування задач із застосуванням елементів теорії ймовірності.
Мета. Засвоїти основні поняття комбінаторики. Знати класичне та статистичне означення ймовірності, теореми додавання та множення ймовірностей, формулу повної ймовірності, формулу Бейєса, формулу Бернуллі, локальну та інтегральну теореми Лапласа.
Теоретичні відомості
Основні поняття комбінаторики
|
Добуток перших
За означенням приймають
Розміщення з
Перестановками з даних
або
Сполученнями, які містять
|
Завдання 1
1. Обчислити значення виразу:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
2. Розв’язати рівняння:
а) ![]()
б) ![]()
в) 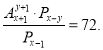
3. Розв’язати систему рівнянь:
а) 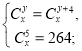
б).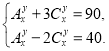
Теоретичні відомості
|
Відносною частотою події називається число
де
Ймовірністю події
|
Теорема додавання ймовірностей
|
Ймовірність суми двох незалежних подій дорівнює сумі їх ймовірностей
Ймовірність суми попарно незалежних подій дорівнює сумі ймовірностей цих подій
Сума ймовірностей протилежних подій дорівнює одиниці
Якщо події
|
Теорема множення ймовірностей
|
Ймовірність добутку двох довільних подій дорівнює ймовірності однієї з них, помноженій на умовну ймовірність другої за умови, що перша подія відбулася
Якщо події
|
Теорема додавання ймовірностей сумісних подій
|
Ймовірність появи хоча б однієї з двох сумісних подій дорівнює сумі ймовірностей цих подій, без ймовірності їх одночасної появи:
|
Формула повної ймовірності
|
|
Формула Бейєса (формула ймовірності гіпотез)
|
|
|
Ймовірність того, що в серії з
|
Локальна теорема Лапласа
|
|
де ![]() (
(![]() не рівне нулеві і одиниці), а
не рівне нулеві і одиниці), а 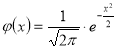 .
.
Інтегральна теорема Лапласа
|
Якщо ймовірність
де
|
|
Ймовірність того, що подія
де
|
Завдання 2
1. В урні ![]() кульок:
кульок: ![]() білих,
білих, ![]() чорних,
чорних, ![]() червоних. Яка ймовірність того, що вийнята з урни кулька червона?
червоних. Яка ймовірність того, що вийнята з урни кулька червона?
2. Три стрільці стріляють по мішені. Ймовірність влучення для першого стрільця дорівнює ![]() , для другого –
, для другого – ![]() , для третього –
, для третього – ![]() . Знайти ймовірність того, що всі три стрільці одночасно влучать у ціль.
. Знайти ймовірність того, що всі три стрільці одночасно влучать у ціль.
3. В ящику ![]() білих і
білих і ![]() чорних кульок. Яка імовірність того, що із двох вилучених кульок одна біла, а друга чорна?
чорних кульок. Яка імовірність того, що із двох вилучених кульок одна біла, а друга чорна?
4. Визначити імовірність того, що в родині, яка має п’ять дітей, буде три дівчинки і два хлопчики. Імовірності народження хлопчика і дівчинки вважаються однаковими.
5. Є три однакові за виглядом ящики. У першому ящику ![]() білих кульок, в другому –
білих кульок, в другому – ![]() білих і
білих і ![]() чорних кульок, у третьому –
чорних кульок, у третьому – ![]() чорних кульок. З вибраного навмання ящика вилучили білу кульку. Обчислити ймовірність того, що кульку вилучили з першого ящика.
чорних кульок. З вибраного навмання ящика вилучили білу кульку. Обчислити ймовірність того, що кульку вилучили з першого ящика.
6. Яка ймовірність того, що при сторазовому підкиданні монети герб з’явиться від сорока до шестидесяти разів?
7. Пристрій складається з десяти незалежно працюючих елементів. Імовірність відмови кожного елемента за час ![]() дорівнює
дорівнює ![]() . За допомогою нерівності Чебишева оцінити ймовірність того, що абсолютна величина різниці між числом елементів, які відмовили і середнім числом (математичним сподіванням) відмов за час
. За допомогою нерівності Чебишева оцінити ймовірність того, що абсолютна величина різниці між числом елементів, які відмовили і середнім числом (математичним сподіванням) відмов за час ![]() виявиться : а) менше двох; б) не менше двох.
виявиться : а) менше двох; б) не менше двох.
Питання для самоконтролю
-
Що означає символ
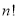 ?
?
- Яка історична подія сприяла виникненню теорії ймовірності, як науки.
- Які основні дії можна виконувати над подіями?
- Як знайти математичне сподівання, дисперсію неперервної випадкової величини?
- Сформулювати теорему Чебишева.


про публікацію авторської розробки
Додати розробку

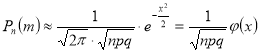 ,
,
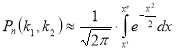 ,
,
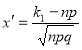 і
і 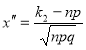 .
.
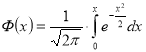 ;
;