Методичні рекомендації підготовки учнів до зовнішнього незалежного оцінювання з математики
НВК «Ерудит»
Ярмарок педагогічної творчості
Розробка вчителя математики
«Методичні рекомендації підготовки учнів до зовнішнього незалежного
оцінювання з математики»
Манько Ліна Анатоліївна
Вчитель вищої категорії
вчитель-методист
Методичні рекомендації підготовки учнів до зовнішнього незалежного оцінювання з математики.
Орієнтація навчального процесу на особистість передбачає підвищення якості математичної підготовки учнів. Тому одним з важливих питань є питання оволодіння нами, вчителями, методикою підготовки учнів до зовнішнього незалежного оцінювання.
Сам процес підготовки до ЗНО передбачає:
- Підвищення якості освіти та запобігання зниженню рівня успішності учнів;
- Використання диференційованого та індивідуального підходу в навчанні та використання інтерактивних методик;
- Формування системи вправ з урахуванням загальних критеріїв оцінювання навчальних досягнень учнів з математики.
Основними компонентами підготовки учнів до зовнішнього незалежного оцінювання з математики є:
- Володіння фактичним матеріалом з основних тем і розділів шкільного курсу математики, сформованість основних знань, умінь, навичок, логічної культури;
- Психолого-педагогічний аспект, який містить сформованість вольових рис характеру, емоційної врівноваженості, моральної підготовки.
Обидва компоненти однаково важливі, оскільки відомо, що емоційний стан, нестриманість, особливості темпераменту можуть негативно позначитися на результатах ЗНО.
Впевнено учні будуть себе почувати, якщо матимуть глибокі знання з математики, вільно володітимуть фактичним матеріалом. Тому головну увагу слід приділяти математичній підготовці учнів до зовнішнього незалежного оцінювання.
Готувати учнів до зовнішнього незалежного оцінювання необхідно під час навчального процесу. Бажано включати в зміст уроків кожного року навчання тестові завдання різних форм: тести множинного вибору, альтернативні тести, перехресного вибору, завдання з короткою відповіддю та розгорнутою відповіддю, аналогічні до тих, що зустрічаються на зовнішньому незалежному оцінюванні. Робити це потрібно не тільки в старших класах. Такі завдання мають як навчальну, так і контролюючу функції. Проте слід звернути увагу учнів, що основним джерелом підготовки до оцінювання був і залишається підручник, а тести допомагають здійснити перевірку. Значну увагу слід приділяти узагальненню та систематизації знань учнів, використовуючи уроки узагальнення та систематизації. Це допоможе учням швидше зорієнтуватися під час випробування. Такі уроки доцільно проводити і в межах конкретно взятої теми, і в рамках всього шкільного курсу математики, і на рівні між предметних зв’язків.
Ми повинні зосередити увагу учнів на розв’язуванні завдань, які найчастіше викликають труднощі. До таких завдань можна віднести текстові задачі, задачі на відсоткові розрахунки, завдання з параметрами, також складними для учнів виявляються завдання з розділів «Тригонометрія», «Елементи комбінаторики, початки теорії ймовірності» та розв’язування стереометричних задач.
Аналіз тестових завдань, запропонованих на зовнішньому незалежному оцінюванні, показує, що деякі з них мають незрозуміле для учнів формулювання. Заміна звичних формулювань умов задач призводить до втрати бажаних балів. Тому під час підготовки учнів до тестування необхідно приділяти увагу вмінню формулювати умови та вимоги до завдань.
Специфіка оцінювання навчальних досягнень учнів у формі тестування така, що деякі знайдені результати треба вміти подавати в незвичайній для учнів формі. Наприклад, указати найменший цілий розв’язок нерівності, або знайти якусь залежність між знайденими коренями рівняння. Тому необхідно формувати в учнів уміння правильно записувати відповіді до завдань з урахуванням умови.
Як показує досвід, багато учнів засвоюють теоретичний зміст курсу математики старшої школи формально, що призводить до звичайного вгадування або до появи неможливих відповідей. Тому слід уникати формального заучування учнями навчального матеріалу.
У ході проведення зовнішнього незалежного оцінювання виявилося, що в учнів недостатньо розвинені навички виконувати математичні записи, що призводить до втрати балів завдань з розгорнутою відповіддю (більшою мірою це стосується задач зі стереометрії та завдань з параметрами). Тому вчителям слід проаналізувати критерії оцінювання завдань з розгорнутою відповіддю та приділяти більше уваги формуванню в учнів математичної культури записів.
Отже, психолого-педагогічні поради та методичні рекомендації відіграють важливу роль стосовно якісної підготовки учнів до зовнішнього незалежного оцінювання з математики. Учитель повинен враховувати психологічній аспект – не ображати і не травмувати учнів; налаштовувати їх на подолання труднощів та досягнення успіху; застосувати на уроках тестові форми завдань з використанням самооцінювання та взаємооцінювання.
Під час підготовки учнів до ЗНО звертаю увагу на наступні вправи:
-
При яких значеннях параметра a рівняння
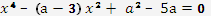 має три різних корені?
має три різних корені?
Розв’язання
Біквадратне рівняння має 3 корені тільки тоді, коли один із коренів дорівнює 0. Дане рівняння має коренем число 0, якщо ![]() , тобто якщо
, тобто якщо ![]() або
або ![]() .
.
Якщо ![]() , отримуємо рівняння
, отримуємо рівняння ![]()
Якщо ![]() , маємо рівняння
, маємо рівняння ![]()
Отже, дане рівняння має точно три різних корені тільки при ![]()
Відповідь: 5
-
При яких натуральних значеннях
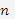 многочлен
многочлен 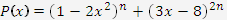 ділится націло на многочлен
ділится націло на многочлен 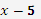 ?
?
Розв’язання
Якщо многочлен ![]() націло ділиться на
націло ділиться на ![]() є коренем даного многочлена. Тоді
є коренем даного многочлена. Тоді ![]() Вираз
Вираз ![]() тоді і тільки тоді, коли
тоді і тільки тоді, коли ![]()
Відповідь: при непарних ![]() .
.
-
Знайдіть усі значення параметра
 , при яких система
, при яких система 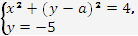 має єдиний розв’язок. У відповідь запишіть їх суму.
має єдиний розв’язок. У відповідь запишіть їх суму.
Розв’язок
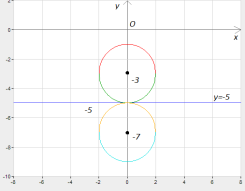 Графіком рівняння
Графіком рівняння ![]() є коло з центром у точці
є коло з центром у точці ![]() і радіусом
і радіусом ![]() . Графіком рівняння
. Графіком рівняння ![]() є пряма, яка паралельна осі OX і яка проходить через точку (0; -5). Система має єдиний розв’язок, якщо пряма дотикається до кола. Це можливо, якщо
є пряма, яка паралельна осі OX і яка проходить через точку (0; -5). Система має єдиний розв’язок, якщо пряма дотикається до кола. Це можливо, якщо ![]() або
або ![]()
Тоді ![]()
Відповідь: -10.
-
При яких значеннях параметра
 система
система 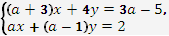 не має розв’язків?
не має розв’язків?
Розв’язання
Cистема ![]() не має розв’язків тоді і тільки тоді, коли
не має розв’язків тоді і тільки тоді, коли![]() .
.
Тоді 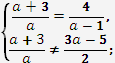
![]()
![]()
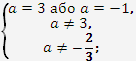
![]()
Відповідь: ![]()
- На лузі біля річки треба обгородити ділянку прямокутної форми, що прилягає до прямолінійного берега річки (з боку річки огорожа не встановлюється) (див. рисунок). Завезено 200 погонних метрів огорожі. Якими повинні бути розміри відповідного прямокутника, щоб його площа була найбільшою?
Розв’язання
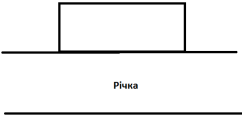 Нехай x м - ширина прямокутника. Тоді довжина прямокутника (200 – 2x) м, а його площа дорівнюватиме
Нехай x м - ширина прямокутника. Тоді довжина прямокутника (200 – 2x) м, а його площа дорівнюватиме ![]() , де
, де ![]() Дослідимо функцію
Дослідимо функцію ![]() на найбільше і найменше значення на відрізку [0;100]. Оскільки
на найбільше і найменше значення на відрізку [0;100]. Оскільки ![]() то
то ![]() , якщо 200 – 4x = 0. Звідси
, якщо 200 – 4x = 0. Звідси ![]() - критична точка функції
- критична точка функції ![]()
Оскільки ![]() ,
, ![]() ,
, ![]() то функція
то функція ![]() набуває найбільшого значення в точці
набуває найбільшого значення в точці ![]() і воно дорівнює 5000. Отже, розміри шуканого прямокутника 50м і 100м, а найбільша площа дорівнюватиме 5000
і воно дорівнює 5000. Отже, розміри шуканого прямокутника 50м і 100м, а найбільша площа дорівнюватиме 5000![]() .
.
Відповідь: 50м і 100м.
-
Знайдіть усі значення параметра
 , при яких рівнянняy 2x³ + 3x² – 12x – a = 0 має точно три корені.
, при яких рівнянняy 2x³ + 3x² – 12x – a = 0 має точно три корені.
Розв’язання
Побудуємо графік функції ![]() .
. ![]()
![]()
![]() якщо
якщо ![]() Враховуючи знаки похідної, одержуємо
Враховуючи знаки похідної, одержуємо ![]() . Тоді
. Тоді ![]() . Будуємо графік функції.
. Будуємо графік функції.
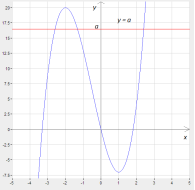
Користуючись побудованим графіком, робимо висновок, що пряма ![]() перетинає графік у трьох точках, якщо
перетинає графік у трьох точках, якщо ![]() . Отже, рівняння має точно три корені, якщо
. Отже, рівняння має точно три корені, якщо ![]() .
.
Відповідь: ![]() .
.
-
Обчисліть інтеграл
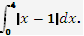
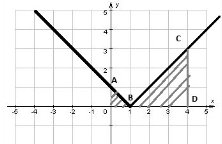 Розв’язання
Розв’язання
Скористаємося геометричним змістом визначеного інтеграла, побудуємо графік функції ![]() Тоді
Тоді ![]()
Відповідь: 5.
Серйозно готуючись до ЗНО учні повинні керуватися формулою: Праця + Знання = Результат (які доданки – така й сума), яка забезпечить їм успіх.


про публікацію авторської розробки
Додати розробку
