Методичні рекомендації "Застосування ігрових технологій при вивченні математики"

Любешівська селищна рада

Заклад загальної середньої освіти  „ Угриничівська гімназія ”

 

 

 

Застосування  ігрових  технологій  при  вивченні  математики

 

Математика 5-9 кл

                                                                

                                                                Комара  Миколи  Івановича

 

                                                  

2021

         

 

 

      У методичних рекомендаціях систематизовані матеріали з використанням дидактичних ігор при вивченні  математики у 5-9 класах, які розвивають пізнавальну активність здобувачів освіти, полегшують сприйняття знань, урізноманітнюють процес навчання.

       Методичні рекомендації містять теоретичні засади щодо упровадження сучасних ігрових технологій на уроках математики і в позакласній діяльності.

       Робота допоможе вчителям математики цікаво, неординарно і змістовно провести заняття та поглибити знання здобувачів освіти, розвинути в них творчі здібності.

      Методичні рекомендації адресовані вчителям, здобувачам освіти, батькам, широкому колу шанувальників математики.

  

 Автор – упорядник:

   Комар  Микола  Іванович, учитель  математики      

 ЗЗСО  « Угриничівська  гімназія »

 

 

 

 

 

Зміст

 

             Вступ  ………………………………………………………………... 4

          І. Основна  частина

1.      Дидактична гра як форма навчання ………………………….  8
2.      Математика і шахи ….………………………………………… 23
3.      Гра судоку  …………………………………………………….  28
4.      Задачі з сірниками …………………………………………….  31
5.      PISA: математична грамотність  ……………………………..  35
6.      Конкурси, вікторини, ребуси   ………………………………..  42
7.      Вислови видатних людей про математику  ………………….  48

        Висновки  …………………………………………………………..  59

  Список використаних джерел …………………………………….  60                   Додатки

  Додаток № 1 ………………………………………………………..  61

  Додаток № 2 ………………………………………………………..  67

  Додаток № 3 ………………………………………………………..  69

  Додаток № 4 ………………………………………………………..  76

 

Вступ

 

                                                   Гра дає можливість відшукати

                                             себе в суспільстві,  себе в людстві,                                                        себе у Всесвіті.

Я. Корчак

             

 

 

 

 

            « Сьогодні знову буде щось цікаве ? » — з надією запитують діти вчителя.  Вони добре знають, що на  уроках будуть не просто розв’язувати нудні приклади, а збирати з геометричних фігур різні об’єкти, розшифровувати малюнки чи складати математичні пазли. Так, це все НУШ у дії. Молодші школярі не уявляють своє життя і навчання без гри, яка є невід′ємною частиною педагогічного процесу. Гра в освітньому середовищі створює мотивацію, близьку до природної, збуджує інтерес, підвищує рівень навчальної праці, розвиває комунікативні навички. Порівняно з іншими формами освітнього процесу, перевага гри полягає в тому, що вона досягає своєї мети непомітно для вихованця, тобто,  не потребує ніяких способів насильства над особистістю дитини.

 Створення ігрових ситуацій на уроках математики у молодших школярів підвищує інтерес до предмету, вносить різноманітність, емоційне забарвлення у навчальну роботу, знімає втому, розвиває кмітливість і спостережливість. Математичні ігри - це той інструмент, за допомогою якого відшліфовується розум дитини, розвиваються його пізнавальні сили, нахили і здібності. Вміло використовуючи ігрові ситуації, можна подати будь-який математичний матеріал дохідливо, доступно, зрозуміло, а, отже, і цікаво.

І ось дитина приходить у 5 клас. Постає питання : може досить гратися, бо ви вже великі ? Ні, грати і гратися необхідно продовжити. Дитина трішки змінилася, але бажання сприймати дійсність через гру залишилося і має бути розвинутим і надалі.

Неабиякого значення грі надавав педагог Шмаков, який відзначав: « Гра — найцікавіше явище культури... Гра, як тінь, народилася разом з дитиною, стала його супутником, вірним товаришем. Вона заслуговує на велику людську повагу, набагато більшу, ніж проявляють до неї люди сьогодні за ті значні виховні резерви, за величезні, закладені в ній педагогічні можливості».

Гра супроводжує людину протягом усього життя, протягом усього існування людства. Адже, в якійсь мірі, усе наше життя — це гра. Навіть стаючи дорослими,  опиняючись  у  певних життєвих  ситуаціях,  ми приміряємо на себе ту чи іншу роль. А для дитини гра — це основний вид діяльності, це засіб взаємодії з навколишнім світом, засіб його пізнання. Недаремно гру називають королевою дитинства. Тому, звичайно, потенціал гри повинен бути використаний і у навчальному процесі. Адже за вмілого використання гра може стати незамінним помічником педагога. Психологи стверджують, що гра може стати одночасно й засобом самовдосконалення, до того ж — й стимулятором доброго настрою. З іншого боку, є об'єктивно величезні можливості гри як педагогічного засобу, що збільшує інтелектуальну напруженість, активізує розумові процеси, підвищує інтерес до знань, тренує пам'ять, вміння міркувати логічно тощо. Захопившись грою, діти навіть не помічають, що навчаються.           Гра – це ключ до багатьох математичних замків. Її можливості невичерпні. Вона робить математику доступнішою і цікавішою, не такою складною, дозволяє дитині відчути у собі впевненість, повірити у власні сили, дарує радість пізнання. Граючись, діти пізнають світ  - яскраво, насичено, змістовно.

     « Якою буде дитина в грі, такою вона буде і в праці, коли виросте. » − писав  А. С. Макаренко.

 

 

                                                                    

1. Дидактична гра як форма навчання

Дидактична гра - це важлива складова навчально–виховного процесу.

Сучасним методом навчання і виховання, що сприяє оптимізації та активізації навчального процесу та дозволяє показати цікаві грані математики, є дидактична гра.

Дидактична гра – це вид діяльності, залучившись до якої, діти навчаються. Поєднання навчальної спрямованості та ігрової форми дозволяє стимулювати невимушене оволодіння конкретним навчальним матеріалом.

Одним із ефективних шляхів розвитку в учнів зацікавленості у навчанні є гра. У процесі гри чудовий світ дитинства поєднується з прекрасним світом науки, до якого потрапляють школярі. Ігри дуже добре поєднуються із «серйозним» навчанням, зацікавившись, діти не помічають, що навчаються, поповнюють свої знання, уміння й навички, здобувають життєві компетентності, розвивають увагу, мислення, самостійність.

У процесі гри реалізується зв'язок головної ролі вчителя й самостійності здобувачів освіти, враховуються вікові та індивідуальні особливості учнів, виконуються принципи наочності, доступності результатів, оскільки навчальна гра забезпечує більш міцне закріплення знань, дозволяє застосовувати їх на практиці, допомагає вчителю контролювати, а учням удосконалювати набуті знання, вміння і навички. Гра сприяє максимальній активізації навчально-пізнавальної діяльності, що є показником ефективності уроку та роботи вчителя. Інтерес і задоволення — надзвичайно важливі психологічні ефекти гри. Гра спочатку приваблює поставленою задачею, труднощами, котрі необхідно подолати, а потім — радість відкриття, відчуття подоланої перешкоди.

        Сьогодення потребує від людини не тільки певної суми знань, умінь та навичок, а, що важливіше, вміння самостійно здобувати й використовувати на практиці нові знання, вміння співпрацювати, спілкуватися, адаптуватися до нових обставин, знаходити шляхи розв’язання  життєвих проблем. Тобто основною метою стає максимальний розвиток компетентності особистості щодо саморегуляції, самоосвіти та самовдосконалення й виховання відчуття постійної потреби до цього.

Звичайно, досягти цієї мети шляхом використання лише традиційних форм та методів організації навчальної діяльності неможливо. Вирішенню цієї проблеми значною мірою сприяє впровадження у навчально-виховний процес активних методів навчання, серед яких провідну роль відіграють навчальні ігри, які дають учням змогу формувати  знання шляхом інтенсивної самостійної пізнавальної діяльності й, разом з тим, сприяють розвитку індивідуальних творчих здібностей.

 

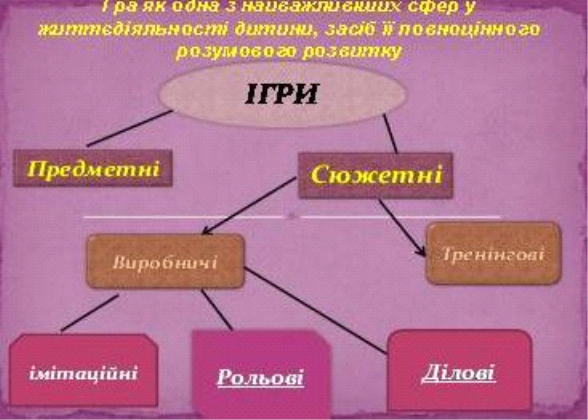
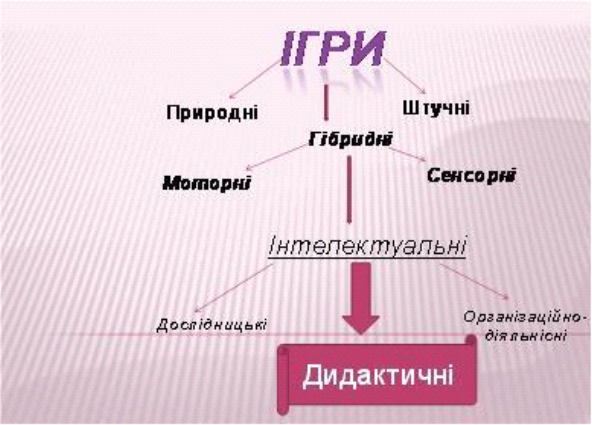
Дидактична гра має чітку структуру, що вирізняє її з-поміж іншої діяльності. Основні структурні компоненти дидактичної гри:

• ігровий задум;
• правила;
• ігрові дії;
•  пізнавальний зміст або дидактичне завдання;
•  обладнання;
•  результат гри.

На відміну від ігор взагалі дидактична гра має суттєву ознаку – наявність чітко визначеної мети навчання і відповідного їй педагогічного результату, що можуть бути обґрунтовані, подані наочно і характеризуються пізнавальною спрямованістю.

Ігровий задум – перший структурний компонент гри, закладений у дидактичне завдання, що необхідно виконати під час навчання. Ігровий задум найчастіше виступає у вигляді питання або загадки, що ніби проектує хід гри. Це надає грі пізнавального характеру, висуває до її учасників певні вимоги щодо знань.

Кожна дидактична гра має свої правила, що визначають порядок дій і поведінку учнів у процесі гри, сприяють створенню на уроці робочої атмосфери. Тому правила дидактичних ігор необхідно розробляти із урахування мети уроку та індивідуальних можливостей учнів. Це створює умови для проявів самостійності, наполегливості, розумової активності, виникнення в учнів почуття задоволення, успіху.

Крім того, правила гри виховують уміння керувати своєю поведінкою, узгоджувати та підпорядковувати її до вимог колективу.

Суттєвими в дидактичній грі є дії, що регламентуються правилами гри, сприяють пізнавальній активності учнів, надають їм змогу виявити свої здібності, застосувати знання, вміння і навички для досягнення цілей гри. Дуже часто ігровим діям передує розв'язання задачі.

Учитель, керуючи грою, спрямовує її в належне дидактичне русло, за необхідності активізує її хід різноманітними прийомами, підтримує інтерес до гри, підбадьорює відстаючих.

Основою дидактичної гри є пізнавальний зміст, що полягає у засвоєнні тих знань і вмінь, які застосовуються під час розв'язування навчальної проблеми, поставленої грою.

Обладнання дидактичної гри значною мірою включає в себе обладнання уроку. Це наявність технічних засобів навчання,  а також різноманітні наочні засоби: таблиці,  роздатковий дидактичний матеріал.

Дидактична гра має певний результат – фінал, що надає їй завершеності. Він виступає перш за все у формі розв'язання поставленого навчального завдання і приносить учням моральне і розумове задоволення. Для вчителя результат гри завжди є показником рівня досягнень учнів у засвоєнні та застосуванні знань.

Усі структурні елементи дидактичної гри пов'язані між собою, і відсутність основних з них руйнує гру. Без ігрового задуму, дій та правил, дидактична гра стає або неможливою взагалі або втрачає свою специфічну форму, перетворюється на виконання вказівок, вправ тощо. Тому, готуючись до уроку, що містить дидактичну гру, необхідно скласти сценарій, вказати, скільки часу відводиться на її проведення, врахувати рівень знань та вікові особливості учнів, реалізувати міжпредметні зв'язки.

Поєднання цих елементів, а також їх взаємодія підвищують організованість гри, її ефективність, що призводить до бажаного результату.

Цінність дидактичної гри полягає в тому, що діти, граючи, значною мірою самостійно набувають нових знань, активно допомагаючи одне одному.

Використовуючи дидактичну гру, учитель має зберегти інтерес школярів до неї. За згасання або за його відсутності в жодному разі не треба примусово нав'язувати гру дітям, оскільки примусова гра втрачає своє дидактичне та розвивальне значення, у цьому випадку з ігрової діяльності випадає найцінніше – емоційний компонент.

За наявності інтересу діти беруть участь у грі і навчаються із задоволенням, що позитивно впливає на засвоєння ними знань.

Важливим є яскраве проведення гри. Крім того, учитель повинен і сам залучатися до гри, інакше його вплив і керівництво будуть виглядати не досить природно. Вміння залучатися до гри – також один з показників майстерності.

Проводячи дидактичні ігри, слід поєднувати цікавість і навчання таким чином, щоб вони не заважали, а навпаки, допомагали одне одному. Засоби й способи, що підвищують емоційне ставлення учнів до гри, слід розглядати не як самоціль, а як шлях, що веде до виконання дидактичних завдань.

Математичний бік змісту гри завжди повинен чітко висуватися на перший план. Лише за цієї умови гра буде виконувати свою роль у математичному розвитку школярів і вихованні їх інтересу до математики.

Під час організації дидактичних ігор математичного змісту перш за все необхідно продумати і врахувати такі питання методики:

1. Мета гри. Які математичні вміння й навички учні засвоять у ході гри? Якому моменту гри слід приділити особливу увагу? Які інші виховні цілі передбачити під час проведення гри?
2. Визначення кількості гравців. Кожна гра потребує певної мінімальної або максимальної кількості учасників. Це слід враховувати під час організації гри.
3. Добирання дидактичних матеріалів і посібників, що знадобляться для гри.
4. Продумування питання найменшої витрати часу для ознайомлення учнів з правилами гри.
5. Визначення тривалості гри.
6. Планування засобів забезпечення участі всіх школярів у грі.
7. Спостереження за учнями під час гри.
8. Передбачення можливих змін, що доведеться внести у хід гри, щоб підвищити зацікавленість і активність учнів.

Планування висновків, про які необхідно повідомити учнів після завершення гри (найвдаліші моменти, недоліки, що трапилися у ході гри, результат засвоєння математичних знань, оцінювання учасників гри, зауваження щодо порушення дисципліни тощо. )

Дидактичні ігри добре поєднуються із серйозним навчанням. Включення в урок дидактичної гри та ігрових моментів призводить до того, що процес навчання стає цікавим і захоплюючим, створює бадьорий, спрямований на роботу настрій в учнів, перетворює подолання труднощів на успішне засвоєння навчального матеріалу. Дидактичні ігри слід розглядати як один із видів творчої діяльності, що тісно пов'язаний з іншими видами навчальної роботи.

Доцільність використання дидактичних ігор на різних етапах уроку різна. Наприклад, під час засвоєння нових знань можливості дидактичних ігор значно поступаються більш традиційним формам навчання. Тому ігрові форми занять частіше застосовують під час перевірки результатів навчання, опрацювання навичок, формування вмінь.

Визначення місця дидактичної гри у структурі уроку і поєднання елементів гри з навчанням значною мірою залежить від правильного розуміння вчителем функцій дидактичних ігор та їх класифікації. У першу чергу колективні ігри слід розподілити за дидактичним завданням уроку. Це ігри навчальні, контролюючі, узагальнюючі.

Теоретичні основи використання дидактичних ігор під час             навчання математики в основній школі

У психолого-педагогічній науці накопичений певний досвід використання дидактичних ігор в процесі навчання математики. Проте він стосується переважно навчання дітей дошкільного і молодшого шкільного віку та реалізується в дошкільних навчальних закладах та початкових класах.  Психологічні фактори успішного навчання математики учнів 5-6-х класів та роль навчальних ігор розкрито в дослідженні О.П.Кисіль. Наявні практичний досвід, певне теоретичне обґрунтування та дидактичне забезпечення використання математичних ігор для учнів основної школи в позаурочний час, що відображено в роботах таких авторів, як П.Ю.Германович, Є.І.Гік, А.П.Доморяд, Є.О.Дишинський, Є.Игнатьев, Б.А.Кордемський, А.Я.Котов, Л.М.Лоповок, Є.М.Мінскін та ін. Існує практичний досвід та теоретичне обґрунтування використання дидактичних ігор на уроках математики в 5-6-х класах основної школи, про що говориться в роботах М.В.Кларіна, В.Г. Коваленко, М.І.Микитинської, М.М.Перова, І.К.Данилова. У педагогічній літературі та періодичних виданнях часто зустрічаються приклади дидактичних ігор з математики і для учнів 7-9-х класів основної школи. Так, В.Г.Коваленко крім навчальних ігор для 5-6-х класів наводить приклади дидактичних ігор, які можна провести під час вивчення математики основної школи, вказує на їх роль і функції в процесі навчання математики, описує основні їх структурні компоненти. Проте автор не виділяє особливості, ознаки дидактичних ігор, не веде мову про відмінність між використанням ігор під час навчання математики учнів різних вікових груп, математичних здібностей та особистих якостей, не вказує на доцільність та методику їх використання на різних етапах навчально-виховного процесу.

Кожному вікові властива певна провідна діяльність, а всі інші види або відсутні, або їх прояв обмежений. Провідною діяльністю в підлітковому віці за сучасних умов є спілкування з однолітками та вчителями з питань опанування основ наук, норм поведінки в колективі та суспільстві, навчання спілкуванню та співпраці з іншими людьми а також індивідуальне виконання соціально-важливих справ. Зміна пріоритетів у діяльності підлітків вказує на те, що організовуючи навчальну діяльність на уроках математики, слід віддавати перевагу таким її формам, які б сприяли їх самовираженню і самоствердженню. Такі можливості з'являються у зв'язку з використання дидактичних ігор з передбаченою особистісно-діяльнісною спрямованістю навчально-виховного процесу.

Характерними  ознаками  та основними  вимогами до організації та проведення дидактичних ігор на уроках математики є :

 1)  наявність навчальної задачі (формування, уточнення, систематизація, розвиток певних знань, умінь і навичок, розвиток мислення, виховання певних якостей особистості тощо);

 2)  існування чітко сформульованої та вираженої проблеми з аргументацією мети і завдань діяльності;

 3)  наявність учасників гри, спільне завдання яких - аналіз навчально-ігрової ситуації і прийняття рішень відповідно до призначеної для кожного учасника ролі; присутність учителя, завдання якого - інформувати про хід гри, аналізувати прийняті учнями рішення, своєчасно коригувати дії учнів;

 4)  чіткий розподіл ролей серед учнів і визначення функцій кожного з них; відмінність між ролевими цілями (кожен учасник має певні обов'язки, які не повинен виконувати інший);

 5) наявність системи об'єктивних стимулів (або мотивів), які спонукують учасників гри активно працювати на кінцевий результат;

 6)   створення особливих навчальних умов, так званої ігрової ситуації;

7)   об'єктивність та однорідність умов, правил та обмежуючих факторів для всіх учасників дидактичної гри;

 8) наявність вільного пошуку в грі, що базується на творчості та самодіяльності учнів;

 9)   доступність завдань дидактичної гри;

10)   емоційність гри, наявність естетичного оформлення;

 11)  наявність елементів змагання між командами або окремими учасниками (що підвищує самоконтроль учнів, веде до чіткого виконання встановлених правил та активізації навчально-пізнавальної діяльності учнів);

12) наявність невизначеності, а іноді й конфліктності, що надає грі полемічного характеру;

 13)  неможливість повної формалізації ситуації;

14)  наявність динамічності під час розв'язування математичних завдань та виконання завдань гри.

Методичні   вимоги до організації і проведення дидактичних ігор.

   Дидактичні ігри на уроках математики повинні включати:

 1)  об'єкт моделювання, введення в дидактичну гру;

 2)  опис основних способів взаємодії учасників гри;

 3)  правила взаємодії суб'єктів гри;

 4)  список команд-учасниць;

 5)  розподіл ролей і функцій учасників дидактичної гри;

   6)  інструкцію кожному учаснику або кожній команді щодо участі в грі;

 7)  загальну схему (етапи) проведення гри;

 8) модифікацію;

 9)   способи, умови і критерії підбиття підсумків гри.

Введення дидактичної гри в навчання математики – процес багаторівневий, що включає концептуальний (розроблення понятійного апарату, постановка навчальної задачі, вибір форми гри, часу її проведення), операційний (типологізація навчальної гри, врахування ігрових та навчальних цілей, виготовлення або вибір наочності, визначення місця в навчальному процесі) та технічний (розроблення вказівок, що мають забезпечити коректне управління діяльністю учнів на уроці математики з використанням дидактичної гри) рівні реалізації.

Дослідники виділяють шість основних груп умов ефективності застосування дидактичних ігор на уроках математики в 5-9-х класах основної школи:

 1) умови, що забезпечують формування соціальної і пізнавальної активності як ключових особистісних характеристик підлітка;

 2) умови, що забезпечують розвиток самостійності учнів: діалогова організація діяльності у процесі гри, наявність кінцевого та проміжних результатів на різних стадіях гри, варіативність вибору завдань та початкових умов;

 3) умови, що забезпечують розвиток здатності до самореалізації та саморегуляції навчальної діяльності підлітків у процесі гри;

 4) умови, що забезпечують гармонійну індивідуальність особистості підлітка; доцільне співвідношення образного і логічного компонентів мислення, рівня пізнавальних потреб та можливостей щодо їх реалізації під час виконання завдань гри; розумне поєднання емоційного і раціонального під час навчання;

5) умови, що забезпечують узгодженість особистих прагнень підлітків з суспільно-корисною спрямованістю їх діяльності;

 6) умови, що забезпечують доцільне поєднання педагогічного керівництва і самостійної діяльності учнів, раціональне співвідношення безпосереднього і опосередкованого впливів педагога та колективу на учня .

Результати дослідження вказують на те, що під час організації дидактичних ігор на уроках математики в 5-9-х класах необхідно

дотримуватися таких положень:

 1) правила гри мають бути простими, чітко сформульованими, а математичний зміст матеріалу – доступний розумінню учнів;

 2) завдання гри повинні містити достатню кількість інформації для активної мислительної діяльності підлітків на уроці, що забезпечуватиме досягнення розвивальної та навчальної цілей уроку;

 3) дидактичний матеріал, який використовується в процесі гри, має бути цікавим, педагогічно доцільним і зручним у користуванні;

 4) якщо дидактична гра має характер змагання, то слід забезпечити справедливий і об'єктивний контроль її результатів;

 5) кожен учень має бути активним учасником дидактичної гри;

 6) якщо на уроці математики створюється кілька ігрових ситуацій, то їх варто чергувати за складністю математичного матеріалу, що до них входить, або характером розумових дій, які необхідні для їх виконання; якщо на кількох уроках підряд проводяться дидактичні ігри, які вимагають аналогічних мислительних дій від учнів, то за змістом математичного матеріалу вони мають задовольняти принцип: від простого до складного, від конкретного до абстрактного;

 7) необхідно дотримуватися міри використання дидактичних ігор у навчанні, щоб учні не звикли в усьому бачити тільки гру;

8) під час дидактичної гри від учнів слід вимагати чіткого і грамотного вираження своїх думок, проведення послідовних логічних міркувань, обґрунтовування висновків;

 9) дидактична гра буде результативнішою, якщо вона закінчиться на тому самому уроці, на якому і розпочалася.

Найбільш ефективними для учнів на етапі вивчення нового матеріалу з математики виявилися такі дидактичні ігри: в процесуальному аспекті за рівнем пізнавальної самостійності – конструктивні і творчі, за часом перебігу – довготривалі, ділові; в управлінському аспекті за способом визначення результатів – вільні, за формою проведення гри – колективні або групові; в соціально-психологічному аспекті за характером ігрового процесу – стратегічні, за включенням виду гри в навчання – художні, загадково-виграшні, за збігом цілей та інтересів суб'єктів гри – спільні за цілями, інтереси можуть збігатися, а можуть бути різними.

Необхідною дидактичною метою навчання математики с оволодіння кожним учнем практичними вміннями і навичками на рівні, який відповідає його навчальним можливостям. У зв'язку з цим учням доводиться розв'язувати велику кількість однотипних завдань, що їх швидко втомлює, призводить до зникнення бажання виконувати вправи, розв'язувати задачі, знижує активність учнів та якість навчання. Таких негативних факторів можна позбутися через використання дидактичних ігор. Відсутність в учнів інтересу до виконання однотипних завдань замінюється в цьому випадку інтересом до самої гри, слабке бажання учнів робити нецікаву справу підсилюється бажанням виконати умови гри та успішно дійти до її фінішу першими .

У процесуальному аспекті треба надавати перевагу дидактичним іграм: на рівні пізнавальної самостійності учнів - конструктивним і творчим; за логікою чергування кроків гри (логічними ознаками) -дедуктивним на уроках геометрії та індуктивним на уроках алгебри; за способом прийняття ігрових рішень - комбінованим; за часом перебігу гри - короткочасним для діагностичного і поточного контролю та довготривалим для проведення підсумкового контролю. В управлінському аспекті дієвими виявилися дидактичні ігри: за формою організації контролю - усні для перевірки теоретичних знань, письмові та з використанням комп'ютерних програм для контролю за оволодінням уміннями та навичками; за способом визначення результатів рішень, які приймаються - жорсткі та контурні; за формою проведення дидактичної гри - індивідуальні або групові (в останньому випадку - з чіткою регламентацією дій та визначеністю обсягу роботи для кожного члена групи). У соціально-психологічному аспекті надавати перевагу дидактичним іграм: за характером ігрового процесу - стратегічним; за включенням гри в процес навчання - ігри-змагання; за збігом чи відмінністю цілей та інтересів - з однаковими цілями та інтересами .

Учителю для проведення дидактичної гри контролюючого характеру під час навчально-пізнавальної діяльності на уроках математики в 5-9-х класах необхідно:

 1)  залежно від етапу навчання визначити мету проведення контролю і його призначення;

 2) дібрати доцільні запитання або задачний матеріал, на основі яких буде здійснюватися контроль знань, умінь і навичок дітей з урахуванням їхніх індивідуальних особливостей;

 3) визначитися у виборі форми контролю та форми проведення навчальної гри;

 4)  розподілити дібрані завдання між етапами гри залежно від виду і функцій контролю та ігрового задуму;

 5)  якщо того вимагає ігровий задум, повідомити учням, яку підготовчу роботу їм треба виконати, з яким домашнім завданням справитися.

Одне з провідних місць у навчальному процесі на сучасному етапі розвитку освіти належить комп'ютерним технологіям навчання. Численне якісне програмне забезпечення, що ефективно можна використовувати під час організації дидактичних ігор на уроках математики в 5-9-х класах, сприяє вихованню інтуїції, розвитку евристичного мислення, фантазії, елементарних дослідницьких навичок, уміння оперувати образами, постійно захоплює гравця перспективою, швидкою зміною зображень, персонажів, прихованих стимулів.

 

 

2. Математика  і  шахи

 

            Математика з моменту появи шахів була тісно пов’язана з цією

 захоплюючою грою.

 

Елементи гри в шахи у математиці

     Математика 6 клас ( автори А. Г. Мерзляк та ін.), с. 32,     вправа № 137

      Автори часто використовують ігрові елементи у своєму підручнику, розвиваючи зацікавленість учнів.

 

 

    Розв’язок. Кінь перебуває на полі а1, а має опинитися на полі h8. Всіх клітинок 64, отже, 63 ходи. 1-й хід – біла клітинка, 2-й хід – чорна клітинка, 3-й хід – біла клітинка, 4-й хід – чорна клітинка, і т.д. Як бачимо, парні ходи припадають на чорну клітинку, а непарні – на білу. Тому 63 – й хід має бути на білу клітинку.

     Відповідь :  ні, не може.

 

Якщо змінити умову задачі : чи може кінь з поля а1 обійти всю дошку

за 63 ходи, то відповідь буде ствердна.

 

                    Математика 6 клас (автори А.Г. Мерзляк та ін.), 2020 р.

                                              Вправа  № 1236, с. 336

 

                    Розв’язання

    На шаховій дошці всього 8 х 8 = 64 клітинки. Нехай заплямованих клітинок буде х, тоді чистих буде ( х + 17 ). За умовою задачі складаємо рівняння :

                х + х + 17 = 64 ;

               2 х = 64 – 17 = 47 ;

               х = 47 : 2 = 23,5 , що неможливо, бо х – натуральне число.

     Відповідь : Ні, не може .

Вправа  № 1167, с. 321

                    Розв’язання

   На шаховій дошці всього 8 х 8 = 64 клітинки, 32 білих і 32 чорних. За умовою і позначенням поля а8  і  h1 є білими клітинками. Кісточка доміно – це прямокутничок 1 х 2, що має 1 білу і 1 чорну клітинки.  Кісточками доміно можна замостити 30 білих і 30 чорних клітинок, і ще 2 чорних клітинки залишилося.      Відповідь :  Ні, неможна .

Вправа  № 816, с. 230

                                                   П. 45, с. 343

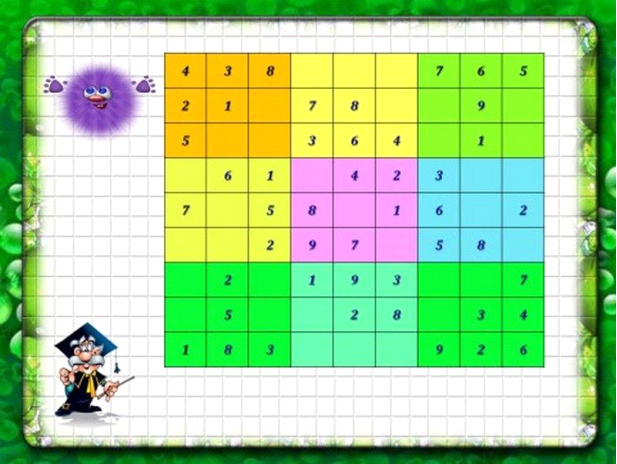
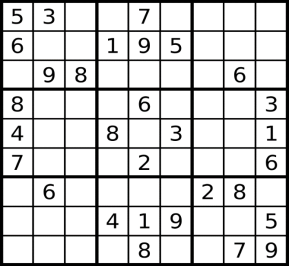
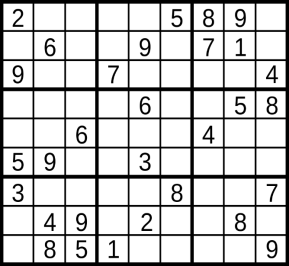
3. Гра « судоку »

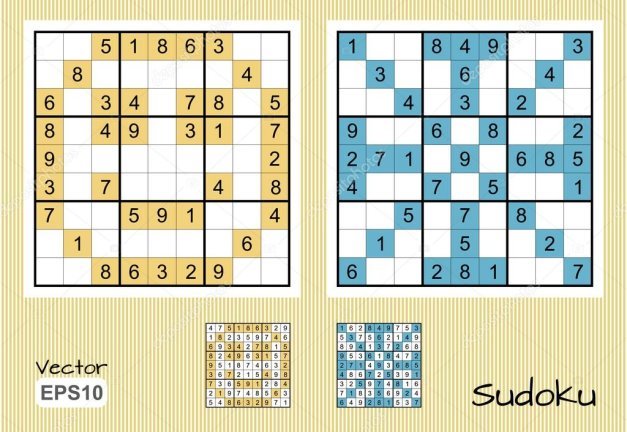
              Судоку ( яп.) – гра,  головоломка  з числами.  Іноді судоку називають магічним квадратом , що в загальному-то не так, тому що судоку є латинським квадратом 9-го порядку. Судоку активно публікують газети і журнали різних країн світу, збірники судоку видаються великими тиражами. Рішення судоку - популярний вид для навчання і дозвілля.

       Ігрове поле являє собою квадрат розміром 9 × 9, розділений на менші квадрати зі стороною в 3 клітини. Таким чином, все ігрове поле складається з 81 клітини. У них вже на початку гри стоять деякі числа (від 1 до 9), звані підказками . Від гравця потрібно заповнити вільні клітини цифрами від 1 до 9 так, щоб в кожному рядку, в кожному стовпці і в кожному малому квадраті 3 × 3 кожна цифра зустрічалася б тільки один раз.

      Складність судоку залежить від кількості спочатку заповнених клітин і від методів, які потрібно застосовувати для її вирішення. Найпростіші вирішуються дедуктивно: завжди є хоча б одна клітина, куди підходить тільки одне число. Деякі головоломки можна вирішити за кілька хвилин, на інші можна витратити години.

      Правильно складена головоломка має тільки одне рішення. Проте, на деяких сайтах в інтернеті під виглядом ускладнених головоломок користувачеві пропонуються варіанти судоку з декількома варіантами рішення.

      Кращий метод вирішення - записувати числа-кандидати в вершині лівого кута комірки, а потім викреслювати неможливі за правилами гри числа з даного осередку. Після цього можна побачити саме ті числа, які можуть займати дану комірку. Грати в судоку рекомендується повільно, так як це розслаблююча гра.

     Спочатку дивляться на ряди, стовпці і блоки 3 × 3 з найбільш заповненими квадратами: легше вирішити там, де варіантів менше. При заповненні комірки потрібно перевірити стовпець, ряд і блок  3 × 3. Потрібно перевірити, що всі інші 8 чисел не дублюються.

      Коли в судоку залишилося кілька відкритих осередків в блоці 3 × 3 і тільки одна комірка підходить для даного числа, то саме це число потрібно записати в дану комірку. Перед заповненням слід упевнитися, що вписується в клітинку число не зустрічатиметься в іншому осередку в тому ж стовпці, рядку або в блоці 3 × 3.

      Коли в одному стовпці, рядку, або блоці 3 × 3 три будь-яких осередки мають числа-кандидати {1,2; 1,2; 1,3}, то число для третьої осередку повинно бути 3. Тому що, якби це було число 1, то в одній з перших двох осередків було б число 2, а в іншої не було б нічого, але такого бути не може, оскільки всі клітини повинні бути заповнені.

      Є дві стратегії, які використовуються для збільшення швидкості рішення головоломки.

      Вибрати число, яке було знайдено для більшості рядків, стовпців або блоків 3 × 3 в судоку. Для кожного блоку 3 × 3, який не містить це число, шукаються інші блоки 3 × 3 в тому ж самому ряду і стовпці блоків 3 × 3, які містять це «найбільш вирішена число» і в вирішуваному блоці, виключаються місця, де це число , не може бути вписано в клітинку. Таким чином знайдеться єдиний осередок для цього числа.                 

 

 

 

 

 

4. Задачі з сірниками

 

 

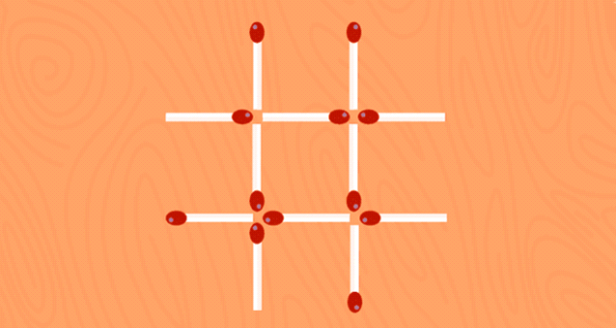
        Головоломки з сірниками -  одне з наймолодших різновидів завдань. Інтерес до вирішення і створення класичних головоломок людина проявляла вже з самих витоків цивілізації. Фізичні та логічні задачі також залишаються популярними з часів глибокої давнини. 

       Інтерес людства до всіляких головоломок завжди підігрівало бажання краще пізнати і зрозуміти навколишній світ. Головоломки, в тому числі і завдання з сірниками, є відмінними помічниками в досягненні поставленої мети.

       Поява завдань стало можливим завдяки винаходу самих сірників. Цей процес розтягнувся на кілька століть і про нього варто поговорити більш детально.

Поява головоломок з сірниками                                                               Відомості про перші головоломки з схожим принципом постановки завдань доходять до нас з часів стародавнього Китаю. Для вирішення завдань використовувався набір бамбукових паличок однакового розміру.

         Друге життя завданням дали шведи. Уже в кінці дев'ятнадцятого століття в Швеції вийшла перша збірка головоломок, і відразу ж здобув популярність серед широких верств населення.

        Різкий стрибок популярності головоломок став можливий завдяки збігу кількох, на перший погляд, не пов'язаних один з одним обставин.

              Причини популярності завдань із сірниками в XX столітті

     -  Одвічне інтерес людей до головоломок

     -  Популярність сірників 

       Людина завжди мала з собою в кишені коробочку сірників, їхня простота і доступність вражала. У будь - якому колективі сірники легко трансформувались в генератор цікавих завдань.

      У нашому побуті сірники поступово відіграють меншу роль. Але як головоломки, збирання фігур не втрачає актуальності і залишається таким же цікавим заняттям для багатьох дітей і дорослих. Збираючи фігури, дитина розвиває моторику, просторове і логічне мислення. Завдяки таким завданням, дитина вчиться виявляти креативність для вирішення проблемних завдань. І головне, що крім користі, дитина отримує задоволення від процесу в пошуках  правильної  відповіді .

Застосування у курсі математики

Підручник математики 5 кл. ( автори А. Г. Мерзляк та ін. ),  2018 р.

С. 104, вправа № 426

 

                                Розвﹸязок : 1)

1   4                       5

2             6

3   7

               8                             9                           10

2)

1 7

2 8

3 9

4 10

5 11

6 12           13

          14                  15                   16                   17                   18                   19

        Головоломки з сірниками – це відмінний спосіб невимушеного розвитку кмітливості, уваги та конструкторських навичок як у дошкільнят, так і у старшокласників! До того ж це прекрасна розвага! 

      Такого типу завдання вже давно використовуються для розвитку логічного та креативного мислення. Популярність подібних вправ обумовлена ​​зручністю використання і доступністю матеріалу, з якого складаються цікаві геометричні та арифметичні фігури.

          Ключові правила розв'язання сірникових головоломок

       Сенс будь-якої головоломки такого типу полягає у тому, що для її вирішення необхідно перекласти один або декілька сірників таким чином, щоб виконати певну умову. Причому, рішення такого завдання, як правило, потребує нестандартного підходу. 

     При розв'язанні головоломок враховуйте наступні особливості:

1. Для розв'язання головоломки, як правило, потрібно знайти нетипове рішення. Слід враховувати, що сірники можуть накладатися одне на одне, переміщуватись у будь-якому напрямку чи перевертатися (якщо виключення цих дій тільки-но не вказане в умові виконання завдання!).
2.     Для розв'язання завдання необхідно розглядати умову дещо ширше за звичайні. Наприклад, для виконання умови щодо побудови певної кількості геометричних фігур шляхом перекладання декількох сірників, потрібно враховувати, що декілька маленьких фігур можуть утворювати  подібну їм велику фігуру.
3.     Для вирішення завдань такого типу потрібна неабияка зосередженість, тож відповідь потрібно шукати, послідовно і не поспішаючи перебираючи можливі варіанти. 

         

          Коли дитина виконує завдання з сірниками, вона:

•                   тренує короткочасну пам’ять і уяву;
•                   вчиться застосовувати нестандартні підходи до вирішення задач;
•                   розвиває просторове і логічне мислення.

 

 

 

5. PISA: математична грамотність

      У 2016 р. Україна долучилася до одного з найбільш масових досліджень – PISA (Programme for International Student Assessment), запровадженого й підтримуваного Організацією економічного співробітництва та розвитку (ОЕСР ). PISA вивчає те, наскільки 15-річні підлітки здатні навчальні здобутки використовувати в різноманітних життєвих ситуаціях для розв’язування особистісно й суспільно значущих проблем. Це міжнародне дослідження зосереджене на найважливіших напрямах навчання, а саме: читацька грамотність (reading literacy), математична грамотність (mathematical literacy) та природничо-наукова грамотність (science literacy).      Результати дослідження використовують для прийняття обґрунтованих політичних рішень у галузі національної освіти. У 2018 р. особливу увагу в дослідженні PISA приділено читацькій грамотності як провідній галузі оцінювання чергового трирічного циклу. До цього читацька грамотність була провідною галуззю у 2000 р. та 2009 р. Математична грамотність була основною галуззю у 2012 р. Особливого значення для України цей міжнародний проект набуває з огляду на те, що в нашій країні започатковані важливі реформи, спрямовані на підвищення якості освіти, зокрема й на перегляд змісту навчання математики. Це дослідження сприятиме усвідомленню місця математики в українській школі та її змісту, адже розуміння математичної компетентності як однієї з вимірюваних у PISA ключових компетентностей не вповні відповідає усталеній в Україні традиції навчання математики в школі. З огляду на це надзвичайно важливим і корисним для освітян України є те, що ОЕСР надала можливість ознайомитися з матеріалами PISA, які ґрунтуються на багаторічних дослідженнях у галузі освітніх вимірювань.

                       

                       Визначення математичної грамотності

       Математична грамотність – це здатність людини формулювати, застосовувати й інтерпретувати математику в різноманітних контекстах. Вона включає математичні міркування й застосування математичних понять, процедур, фактів та інструментів для опису, пояснення й прогнозування явищ. Вона допомагає зрозуміти роль математики у світі, робити аргументовані умовиводи й приймати рішення, необхідні людям як творчим, активним і мислячим громадянам. У сучасному світі розуміння математики є надзвичайно важливим для підготовки молодих людей до життя. Збільшення кількості проблем і ситуацій, із якими молодь стикається щодня, зокрема й у професійних контекстах, потребує певного рівня розуміння математики, здатності до математичного обґрунтування й використання математичних інструментів, щоб надалі ці проблеми можна було цілковито усвідомити й розв’язати. Математика є критично важливим інструментом для молоді, оскільки проблеми й виклики очікують на молоде покоління і в особистому, і в професійному, і в суспільному, і в науковому аспектах життя. Тому надзвичайно важливо розуміти, наскільки юнаки й дівчата, які тільки-но закінчили навчання в школі, адекватно підготовлені для того, щоб застосовувати математику для розуміння важливих питань і розв’язування значущих проблем. Тестування 15-річних підлітків дає можливість визначити ранні ознаки того, яким чином учні/студенти зможуть реагувати на різні майбутні життєві ситуації, що містять математичний складник. Під час оцінювання знань 15-річних підлітків доцільно поставити запитання :   «Якими знаннями важливо володіти особі, щоб бути здатною ефективно діяти в ситуаціях, що пов’язані з математикою?» Або конкретніше: «Що означає математична компетентність для 15-річної особи, яка готується до закінчення школи або до вступу до професійно-технічного чи вищого навчального закладу?» Згідно із цим рамковим документом, важливо визначити математичну компетентність таким чином, щоб вона акцентувала на здатності учнів/студентів формулювати, застосовувати й інтерпретувати математику в різних контекстах, а не на математичних знаннях і вміннях низького рівня. Визначення, швидше, призначене описувати вміння учнів/студентів математично обґрунтовувати та використовувати математичні поняття, процедури, факти й інструменти для описування, пояснювання та прогнозування явищ. Така концепція математичної грамотності слугує підґрунтям для розвитку в учнів/студентів глибокого розуміння суто математичних понять, а також надає їм переваги в пізнанні абстрактного світу математики. У визначенні математичної грамотності для PISA особливий наголос варто робити на необхідності розвитку вміння учнів/ студентів застосовувати математику в життєвому контексті, для чого необхідно забезпечити їх багатим досвідом використання математики на заняттях у навчальному закладі. Ідеться про тих 15-річних підлітків, хто невдовзі закінчуватиме своє навчання математики в навчальному закладі, а також тих, хто продовжуватиме вивчати її й надалі. Крім того, є підстави стверджувати, що мотивація майже всіх учнів/студентів до вивчення математики зростає, коли вони бачать зв’язок того, чого вони навчаються, із навколишнім світом та іншими дисциплінами. Звичайно ж, математична грамотність не має вікових обмежень. Проте для оцінювання математичної грамотності 15-річних необхідно зважати на їхні вікові характеристики, відповідно до яких має бути визначено зміст, мову й контексти. Цей рамковий документ виділяє широкі категорії змісту, важливі для математичної грамотності людей узагалі, і конкретні математичні теми, важливі саме для 15-річних учнів/студентів. Математична грамотність не є властивістю, яку людина може мати або не мати. Це, така властивість, яку набувають безперервно, завдяки чому одні особи стають більш математично грамотними, ніж інші. Водночас потенціал для її розвитку є завжди.

                                    Практичне  застосування

 

      

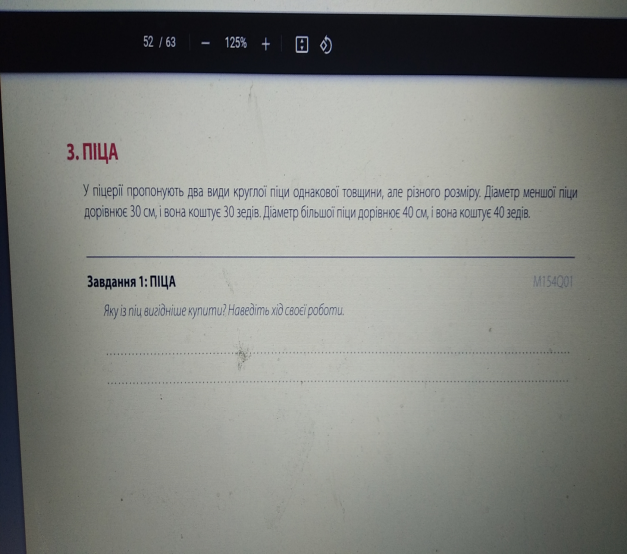
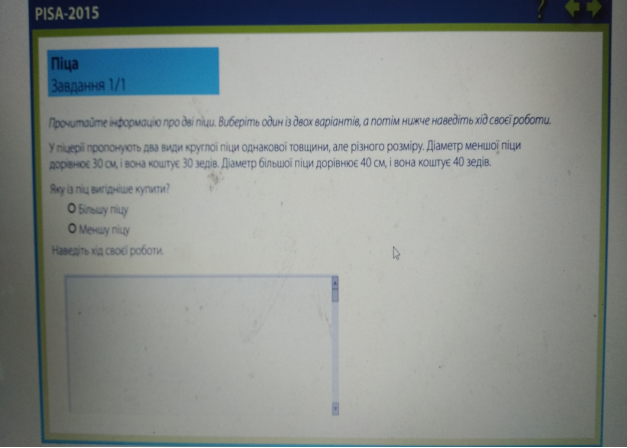
     Завдання № 3 «Піца» належить до категорії особистісного контексту, відомого багатьом 15-річним учасникам. Категорія саме особистісна, оскільки поставлене питання стосується того, яка з піц є найвигіднішою для покупця. Завдання ставить відносно невисоку комунікативну вимогу, пов’язану із читанням, отже, більшість своїх зусиль учасник може докласти до сприйняття математичного підґрунтя, яке лежить в основі цього питання.

    

 

Математика 6 клас ( автори А. Г. Мерзляк та ін.), с. 202,  вправа № 752

   Розвﹸязання :  d₁ = 30 см,   R₁ = 15 см,  d₂ = 20 см,   R₂ = 10 см 

S₁ = = 3,14 ·225 = 706,5 (см – площа круга однієї великої піци ,

S₂ = = 3,14 ·100 = 314 (см – площа круга однієї малої піци ,

S = 2S₂ = 628 (см – площа круга двох малих піц .

  Відповідь :  Дмитрику треба придбати 1 велику піцу, це більше на 1/8 частину (12,5 %).

Завдання № 7 «Клумби» належить до змістової категорії «простір і форма», тому що воно розглядає властивості фігур. Воно пов’язане з професійною контекстною категорією, тому що в ньому йдеться про роботу садівника. За процесом тестове завдання належить до категорії застосування математичних понять, фактів, процедур і міркувань, тому що для його розв’язування необхідно застосувати процедурні знання до конкретних математичних об’єктів. Завдання також певною мірою потребує інтерпретації, застосування й оцінювання математичних результатів, оскільки необхідно пов’язати представлені математичні об’єкти з контекстуальним елементом – обмеженням довжини наявної дерев’яної огорожі.

 

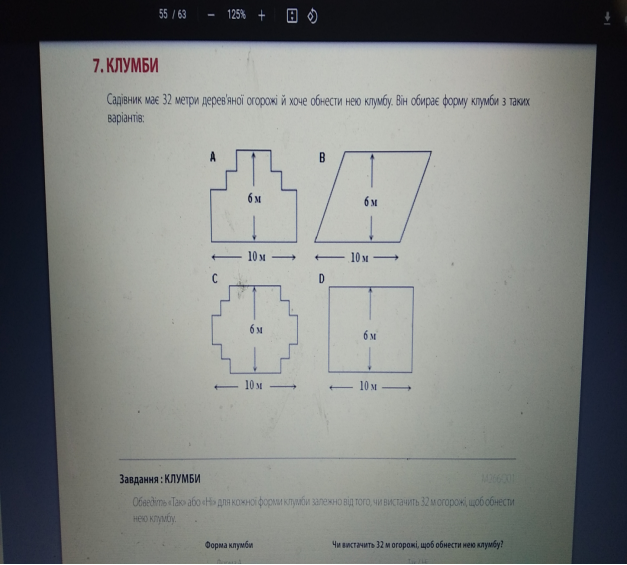
Це завдання було одним із найскладніших завдань : частка правильних відповідей становила трохи менше 20 %. Його можна розв’язати, застосувавши геометричні знання й міркування. У завданні надано достатньо інформації, щоб уможливити обчислення точного периметра форм А, C та D, для яких він однаковий і становить 32 метри. Проте стосовно форми B не надано достатньої інформації, отже, необхідно застосувати інший підхід. Міркування можуть бути такими: тоді як сума довжин «горизонтальних» відрізків для кожної із чотирьох фігур є однаковою, бічні (похилі) сторони форми B є довшими, ніж сума «вертикальних» відрізків кожної з інших фігур.

6. Конкурси, вікторини, ребуси

Гра «Вікторина» №1

Тема: десятковий запис натуральних чисел

Мета гри: актуалізація базових знань і перевірка знань учнів.

Обладнання: набір фігур , картки

Клас поділяється на команди (по рядах). Ставиться запитання. Викликається учень, який першим підняв руку (можливий варіант, коли викликається учень певної команди, що першим підняв руку). Якщо відповідь правильна, команда одержує бал (капітану вручається фігура з набору). У випадку помилки викликається учень іншої команди.

        Зразки запитань і завдань:

• За допомогою скількох цифр записуються натуральні числа?
• Як називається система запису натуральних чисел?
• Які розряди містить клас мільйонів?
• Який клас іде після класу мільйонів зліва? справа?
• Чим відрізняється запис числа у десятковій системі числення від запису в римській нумерації?
• Прочитай числа, записані в десятковій системі (вчитель послідовно записує на дошці): 3 072 000 320, 16 000 003 000, 109 203 007 тощо.
• Вкажи в кожному числі відсутні класи, розряди.
• Прочитай числа, записані в римській нумерації (для сильного класу): XXX, II, IV, XXI, XVII.
• Запиши всі двоцифрові натуральні числа, які більші від 50 і закінчуються трійкою.
•      Запиши всі двоцифрові натуральні числа, сума цифр яких дорівнює п'яти.
•      Запиши число, що має 32 сотні та 15 одиниць.
•      Три перших трицифрових числа, сума цифр яких дорівнює трьом.

 

 

Гра «Математичний хокей»

Тема: додавання натуральних чисел

Мета гри: актуалізувати базові знання з додавання натуральних чисел.

Клас ділиться на дві команди. Кожна команда обирає капітана. Він призначає воротаря. Решта — польові гравці (до дошки виходять четверо).

Вкидання шайби. Арбітр (учитель) ставить запитання. Капітан, який знає відповідь, підносить руку. Відповідає той, хто підніс першим руку. За правильної відповіді «вкидання» виграно. У випадку помилки «вкидання» автоматично виграє суперник.

Той, хто «одержав шайбу», може перетасувати її товаришеві по команді (назвавши його прізвище і поставивши запитання) або «послати в бік воріт суперника» (назвавши прізвище «воротаря» і поставивши йому запитання). «Посилати шайбу» можна лише після встановленого числа (не менше двох) «пасів». Це число встановлює вчитель.

Якщо учень, якому «послано шайбу» затримується з відповіддю, то гравець команди суперників може піднести руку і з дозволу вчителя відповісти. Якщо відповідь правильна, то він «перехоплює шайбу» і «дає пас» товаришеві по команді. Якщо він помилився, йому виставляється «жовта картка» — перше попередження. Відповідає той, кому поставлено запитання.

За правильної відповіді «шайба» в нього, і він діє, як зазначено вище. У випадку помилки «шайба покинула межі поля» і призначається нове «вкидання».

Якщо «воротар» відповів правильно, він «взяв шайбу» і «перетасовує» її товаришеві по команді. Якщо помилився, команді «забито шайбу» і призначається «вкидання».

Гравець, який відповів на запитання, не маючи на це права, одержує «червону картку» — вибуває з гри. Вибуває з гри також гравець, що одержав два попередження.

Можна міняти «капітана» і «польових гравців» після кожного «вкидання» і «воротаря» після кожного «взяття воріт».

Якщо на поставлене запитання не можна відповісти, «шайба покидає поле» і призначається «вкидання».

Завдання для «вкидання шайби»:

1.               Число, що дістанемо в результаті додавання натуральних чисел, називають...
2.               Число, що додаємо, називають...
3.               Запишіть: тридцять два плюс двадцять чотири. Доданками є числа... їх сумою є число...
4.               Знайти суму двох перших трицифрових натуральних чисел.
5.               Число 3 можна записати у вигляді суми двох натуральних чисел так...
6.               Запишіть усі двоцифрові натуральні числа, сума цифр яких дорівнює п'яти.
7.               Якщо число 147 збільшити на 53, то дістанемо...
8.               Знайдіть суму чисел 285 і 389.

9.       Запишіть усі двоцифрові натуральні числа, в яких різниця цифр дорівнює 8.               

10. Знайти суму найменшого трицифрового та найменшого чотирицифрового чисел.

Гра «Математичний брейн-ринг»

Тема: властивості додавання натуральних чисел

Мета гри: повторити і систематизувати знання учнів про переставну і сполучну властивості додавання; сформувати навички застосування властивостей додавання під час розв'язування вправ на додавання.

У грі беруть участь 4 команди. В перших двох турах грають між собою по дві команди, а в третьому зустрічаються переможці перших двох турів. У перших двох турах команди грають до трьох балів. Третій тур — до 5 балів.

                           Перший тур

1.               Знайдіть суму найбільш зручним способом 26+19+34+51.
2.               Як зміниться сума двох доданків, якщо один з доданків збільшити на 125?

3.       Порівняйте значення виразів, не обчислюючи їх:

2056+5126  і  2000+5126.

4.       Спростіть вираз (54+х)+26.

 Знайдіть значення виразу х+у+z, якщо х= 47, у = 68, z = 33.

 Яке число треба поставити замість зірочки, щоб сума 224+*+1276 дорівнювала 2500?

                      Другий тур

1.               Скільки різних двоцифрових чисел можна записати, використовуючи цифри 0; 2; 3; 4?
2.               Обчисліть зручним способом суму 83+127+273+417.
3.               Як зміниться сума, якщо один з доданків збільшити на 23,                     а другий — на 17?
4.               Спростіть вираз (а+47)+53.
5.               Знайдіть значення виразу т+п+р, якщо т = 143, n = 557, p = 106.
6.                 Яке число треба поставити замість зірочки, щоб сума 240+*+637 дорівнювала 1637?

                      Третій тур

  Яке число треба додати до натурального числа, щоб отримати наступне за ним число?

 Заповніть ланцюжок обчислень:

повинен приземлитися кожен десантник, і вкажіть йому шлях, провівши стрілку від вправи до відповіді.

Учні в зошитах розв'язують вправи. Учитель по черзі викликає їх до дошки, і вони послідовно вказують шлях кожного десантника. Решта учнів перевіряє роботу і допомагає в разі потреби.

 

39 :  3 + 16

37 + 12 · 6

(84 - 40) : 4

87 : (62 - 59)

 

 

240 – (60 + 71)

50 - 1 · 3

(36 + 19) : 5

 

109

47

29

11

 

 

Без гри немає і не може бути повноцінного дитячого  розвитку. Гра – це величезне світле вікно, через яке  в духовний світ вливається життєвий потік уявлень…”

                                                            В.О.Сухомлинський

У грi дитина живе, i слiди  цього життя залишаються в   нiй глибше, нiж слiди справжнього життя.

                                                                      К.Ушинський

В арифметиці ставити питання важливіше за вміння їх розв’язувати.
                                                                     Г.Кантор
    Невигадливі головоломки про цілі числа протягом віків були джерелом оновлення математики.
                                                                                      Г. Біркгоф
…Спробуємо на хвилину уявити собі, що ми всі втратили елементарні арифметичні знання. Адже це приведе до справжньої суспільної катастрофи, бо арифметичний розрахунок супроводить нас на кожному кроці.
                                                                   Б. В. Гнєденко
  Грою потрібно просочити все життя дитини

К. Ушинський

   Найдосконаліший мозок іржавіє без дії.
                                                             Шерлок Холмс
     Справа не в тому, що вони не бачать розв’язку. Справа в тому, що вони не бачать проблеми.
                                                          Г. К. Честертон
Найкращий спосіб вивчити що-небудь – це відкрити самому.
                                                      Д. Пойа
Алгебра і геометрія — єдині країни, де панують тиша й мир.
                                                                           М. Аньєзі
Геометрія є пізнання всього існуючого (IV ст. до н. е.).
                                                                         Платон
    Числа — це невід’ємне знаряддя сучасної цивілізації, що використовується для впорядкування сфери її діяльності.
                                                                          Ф. Дейвіс
      Арифметика — це лічильна мудрість. Без цієї мудрості ні філософа, ні лікаря не може бути.
                                                               Л. П. Магницький
Цілі числа — першоджерело математики.
                                                               Г. Мінковський
   Усе впорядковується відповідно до чисел (VI ст. до н.е.).
                                                                         Піфагор
    І, дуже полюбивши мистецтво числове, я подумав, що без числа ніяке міркування філософське не можна вивести, і його слід вважати матір’ю всієї мудрості.
                                                                  Ананія Ширакаці

Жоден учений не мислить формулами.
                                                                 А. Ейнштейн
     Формула – стислий вираз законів природи
                                                                       Я. Черняк
    … Я не фахівець із математики, а тільки прихильник її, невдаха, закоханий у цю найпрекраснішу з наук.     П. Валері                                                                   
                        

 5 мудрих думок про математику від

прогресивних українських вчителів

 

( від команди GIOS )

Сучасні думки про математику

Основна цінність математики ховається за кулісами. Хто відкриває її істинну значущість, вчить мислити аналітично та “прокачує” логічне мислення дитини?

Звичайно, вчителі математики. В чомусь представники цієї професії – герої. Країна має своїх героїв знати, тому ми періодично проводимо інтерв’ю з прогресивними вчителів математики.

1. “Математика значима не лише формулами, за допомогою яких будуються мости і пишуться комп’ютерні програми. Величезна цінність цієї науки – у здатності прокачувати мозок та створювати нові нейронні зв’язки. Математика вчить думати, знаходити різні шляхи подолання проблем та знаходити для них оптимальне рішення. На економічному форумі у Давосі ці компетенції включили у ключові для “виживання” у суспільстві майбутнього.»

Дарина Васильєва

 

      2) "Математика розвиває логіку та вчить наполегливості. Геній – це 1% таланту, інші 99% – наполеглива праця. Науку не можна засвоїти, якщо учень не буде працювати. Якщо ж дитина навчиться володіти собою, своїм часом, силою волі – тоді вона засвоїть і математику. А здобуті навички знадобляться їй в житті”.

 

 

 

 

      3) “Неважливо, який я викладаю предмет. Важливо, які цінності я через це транслюю. Батькам я завжди говорю, що «математика – понад усе». І вважаю, що не помиляюсь, тому що це та наука, яка допомагає навести порядок у наших думках та твердженнях, формує логічне та аналітичне мислення. Вона дає старт сфері ІТ, яка

сьогодні трансформує світ найпотужніше".

 

4) “Світ змінюється і змінюється викладання математики. Необхідно «йти в ногу з часом», як того потребує сучасність. Тому на своїх уроках я використовую дослідницьку діяльність (це напрям моєї дисертації), змішане навчання, користуюсь засобами ІКТ, електронними та мультимедійними пристроями, платформою GIOS, використовую стратегії когнітивної активації. Це подобається моїм учням і мені. Зараз є великі можливості гейміфіковувати освіту та зробити її міждисциплінарною. Вчителі мають навчати не лише математиці  чи історії, а показувати, що математика пов’язана з історією, біологією, музикою і так далі. Завдяки такому підходу, діти зрозуміють певний предмет не абстрактно, а в його зв’язку з усією природою”.

5) “Як вчителі, ми формуємо майбутню особистість, і від цього залежить не тільки життя дітей, а й нас самих. Потім ці учні будуть на керівних посадах держави та формуватимуть майбутнє суспільства. Я вчу дітей мислити та думати. Ситуації, з якими стикаються учні при розв’язуванні задач іноді викликають паніку, страх невдачі. Я хочу показати їм, що помилки – це природно, головне – знайти вихід. Математика вчить аналізувати ситуацію та знаходити оптимальне рішення серед можливих. Це наука точна та логічна. І за це вона мені подобається”.

 

 

 

 

Висновки

         Рівень навченості, розвитку, вихованості та пристосованості учнів основної школи до суспільних умов можна суттєво підвищити, якщо на уроках математики поєднати їх навчальну діяльність з ігровою. Таке поєднання забезпечує задоволення головних вікових потреб учнів у спілкуванні з однолітками та самоствердженні і тому сприяє підвищенню рівня успішності у навчанні.

       Найважливішими умовами організації ігрової діяльності на уроках математики учнів 5-9-х класів з метою покращення якості та успішності навчання, виховання та розвитку підлітків є вибір дидактичної гри, дотримання вимог до змісту та проведення дидактичних ігор, визначення місця і ролі їх у в системі інших видів навчально-пізнавальної діяльності підлітків, вибір доцільних способів керівництва грою.

      Використання дидактичних ігор в процесі вивчення математики  підвищує успішність та якість навчання.

Вміле поєднання індивідуальних, групових та колективних форм навчальної діяльності у процесі дидактичних ігор допомагає учням долати соціально-психологічні та фізіологічні бар'єри, які виникають під час вивчення математики.

Уроки математики в 5-9-х класах, організовані з використанням дидактичних ігор, під час яких учні виступають в ролі консультантів, виконавців, аудиторів тощо, дають змогу виховувати в учнів активність, бажання вивчати математику, розвивають їх пізнавальні інтереси.

 

Список  використаних  джерел

 

1. Вакуленко Т.С. PISA: математична грамотність. - К., 2018.- С.8, 52-54.
2. Грамбовська Л. Коригування методичної системи навчання геометрії основної школи.// Математика в школі. – 2006. №5.– С.56-60.
3. Ельконін Д.Б. Психологія гри – М., 1978. – С.277–312.
4. Коваленко В. Г. Дидактичні ігри на уроках математики. – М., 1990. – С.13
5. Козира В.М. Технологія уроку з математики. –Тернопіль: Астон, 2002.–С.52.
6. Любчак Л. В. Методика організації ігрової діяльності: Практикум /       Л. В. Любчак, К. А. Колеснік. – Вінниця : ЦОП «Документ Принт», 2017. – С.196.                                 
7. Микитин О.В. Використання дидактичних ігор на уроках математики.// Математика.–2004.–№38.– С.37–45.
8. https://naurok.com.ua/post/rozvivalni-nastilni-igri-yaki-mozhna-vikoristati-na-urokah
9. Романенко А.О. Математика і комп’ютерні технології // Комп’тер у школі та сім’ї. –2001. –№1.– С.41– 44.
10.  Слєпкань З.І. Методика навчання математики.–К.: Зодіак– Еко, 2000.–С.512.
11.  Сухарева Л.С. Дидактичні ігри на уроках математики. 7-9 класи.–Харків: Основа, –2006.– С.144.
12.  Тополя Л.В. Дидактичні ігри, їх види, цільове призначення і функції в навчальному процесі //Дидактика математики: проблеми дослідження. – Міжнародний збірник наукових робіт. –Донецьк: ТЕАН, 2001.– Вип.16.– С.167–173.
13.  Ульяницька Л. С. Ігрові проблемні ситуації / Л. С. Ульницька // Початкова школа. – 1993. – №9. – С.27.
14.  Щербань П. Дидактичні ігри в навчально-виховному процесі / П. Щербань // Початкова школа. – 1997. – №9. – С.18.
15.  Якиляшек В. Урок математики з елементами гри / В. Якиляшек // Початкова школа. –1997 – №6.- С.8 - 22.

Додаток № 1

Елементи гри в шахи у математиці

Якщо змінити умову задачі : чи може кінь з поля а1 обійти всю дошку

за 63 ходи, то відповідь буде ствердна.

 Приклади різних способів міркування :

41	34	15	4	43	32	17	6
14	3	42	33	16	5	44	31
35	40		56	59	62	7	18
2	13	58	61	52	55	30	45
39	36	51	54	57	60	19	8
12	1	24	37	50	53	46	29
25	38	11	22	27	48	9	20
0	23	26	49	10	21	28	47

 

 

 

41	20	33	8	43	18	31	6
34	9	42	19	32	7	44	17
21	40			61	58	5	30
10	35	60	57	54	51	16	45
39	22	37	52	59	56	29	4
36	11	24	55	50	53	46	15
23	38	1	26	13	48	3	28
0	25	12	49	2	27	14	47

 

37	42	19	8	35	44	21	6
18	9	36	43	20	7	34	45
41	38	51	60		62	5	22
10	17	40	57	50	59	46	33
39	56	27	52	61	54	23	4
16	11	14	55	58	49	32	47
13	28	1	26	53	30	3	24
0	15	12	29	2	25	48	31

 

27	20	47	8	29	18	45	6
48	9	28	19	46	7	30	17
21	26	61	50	59	54	5	44
10	49	56	53	62	51	16	31
25	22	37	60	55	58	43	4
38	11	24	57	52	63	32	15
23	36	1	40	13	34	3	42
0	39	12	35	2	41	14	33

 

Ось правильна відповідь ! (власна)

 

 

А це книжний  варіант

 

 

45	26	5	60	31	40	55	10
4	61	44	27	56	9	32	39
25	46	59	6	41	30	11	54
62	3	28	43	8	57	38	33
47	24	7	58	29	42	53	12
2	63	22	15	50	19	34	37
23	48	1	20	17	36	13	52
0	21	16	49	14	51	18	35

 

 

 

 

 

 

 

 

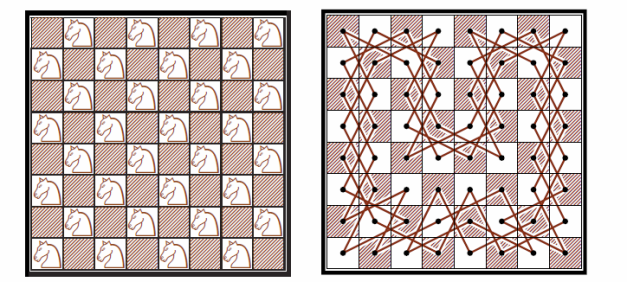
   Також задачу можна розглядати для інших форматів шахової дошки. А) 5 х 5

6	19	8	13	4
9	14	5	18	23
20	7	24	3	12
15	10	1	22	17
0	21	16	11	2

          Б) 7 х 7

8	29	18	35	6	27	16
19	34	7	28	17	36	5
30	9	32	45	42	15	26
33	20	43		47	4	37
10	31	46	41	44	25	14
21	40	1	12	23	38	3
0	11	22	39	2	13	24

8	29	18	33	6	27	16
19	34	7	28	17	40	5
30	9	32	43	46	15	26
35	20	45		41	4	39
10	31	42	47	44	25	14
21	36	1	12	23	38	3
0	11	22	37	2	13	24

8	29	18	47	6	27	16
19	46	7	28	17	34	5
30	9	32	43	40	15	26
45	20	41		33	4	35
10	31	44	39	42	25	14
21	38	1	12	23	36	3
0	11	22	37	2	13	24

 

         49 клітинок, 25 чорних і 24 білих, 48 ходів.

13	26	5	22	11	32
6	23	12	33	4	21
27	14	25		31	10
24	7	16		20	3
15	28	1	18	9	30
0	17	8	29	2	19

В) 6 х 6

 

 

 

 

11	22	5	28	13	20
6	27	12	21	4	29
23	10	25		19	14
26	7	16		30	3
9	24	1	32	15	18
0	33	8	17	2	31

18	5	14	9	20
13	10	19	4	15
6	17	2	11	8
1	12	7	16	3

9	34	3	24	7	32
2	25	8	33	4	23
27	10	35	14	31	6
18	1	26	5	22	15
11	28	17	20	13	30
0	19	12	29	16	21

14	11	22	5	18	9
23	6	13	10	21	4
12	15	2	19	8	17
1	24	7	16	3	20

 

Є правильна відповідь !

 Задача. Обійти конем шахову дошку а ) 4 х 5;  б ) 4 х 6; в ) 4 х 7, побувавши на кожному полі один раз.

Розв’язання (власне)

 

20	7	16	13	28	5	24
17	14	19	6	25	12	27
8	21	2	15	10	23	4
1	18	9	22	3	26	11

 

 

 

 

 

 

     Задача.  На шашковій дошці  5 х 5 розставте максимальну кількість коней, щоб вони не били один одного.

                                   Розв’язання .

  З  25 полів 13 чорних клітинок і 12 білих. 13 коней треба поставити на чорних полях, бо вони б’ють своїм ходом на білі поля.

 

1		2		3
	4		5
6		7		8
	9		10
11		12		13

 

 

 

 

 

    

 

 

Задача. Відновіть по номерах, що залишилися, шлях коня, який побував по одному разу на всіх клітинках шахової дошки

розміром 6 х 6.  

17	24	3	32	11	26
2	31	18	25	4	33
23	16	1	10	27	12
30	9	14	19	34	5
15	22	7	28	13	20
8	29	14	21	6	35

      

 

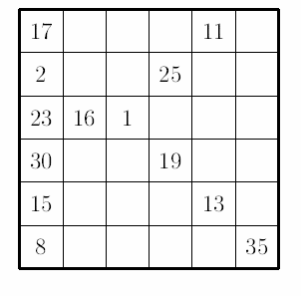
Розв’язання ( власне ) :

                   

Додаток № 2

( гра  судоку )

 

      Застосування .     Алгебра, 9 клас, Бевз 2017, с.23, вправа № 90 :

 

 

 

2	4	5	3	8	7	6	1	9	9
1	9	8	6	5	4	3	2	7	8
7	6	3	1	2	9	5	8	4	7
9	5	7	4	6	2	8	3	1	6
8	3	6	7	1	5	9	4	2	5
4	2	1	9	3	8	7	5	6	4
6	1	4	5	9	3	2	7	8	3
5	8	9	2	7	1	4	6	3	2
3	7	2	8	4	6	1	9	5	1

        a      b      c     d      e      f      g      h      і

Розв’язок : Пронумеруємо для зручності поля буквами і цифрами, так як це зроблено у шаховій дошці. Тоді легше почати роботу і не заплутатися. Порядок роботи буде такий :

        d5, g5, f3, f1, d6, e9, f7, e7, a4, a8, a2, c3, d3, d2, d7, d8,

c1, i4, h4, c9, c6, b6, c4, b4, b7, f6, f4, g3, i3, h3, g6, i6, i2, h1, g1, g9,

i7, h9, i8, i9, b8 …

    Ця гра розвиває спостережливість, далекоглядність , гостроту розуму, вміння опрацьовувати різні варіанти, оцінювати ситуацію.

Додаток № 3

Задачі з сірниками

  Переставте один сірник так, щоб приклад було вирішено правильно.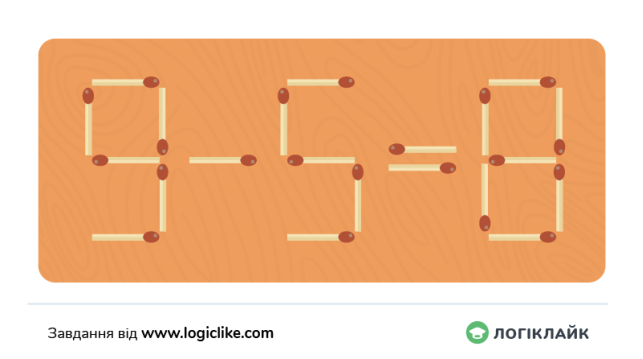

Як можна переставити 1 сірник, щоб рівність стала правильною?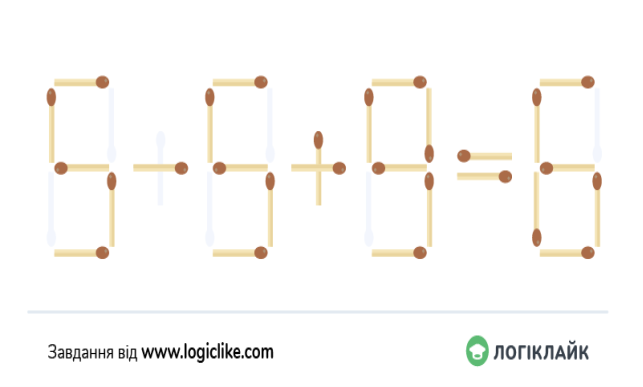

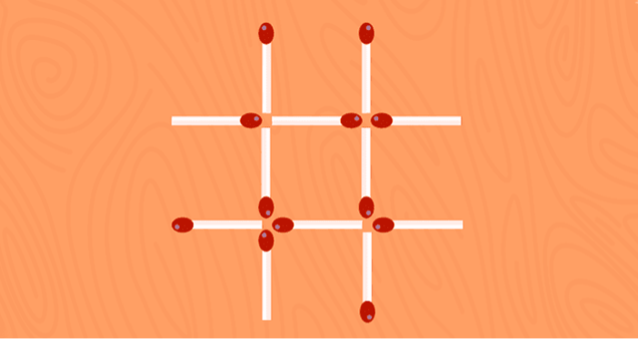
  Потрібно прибрати 2 сірники так, щоб залишилися 4 рівні квадрати.

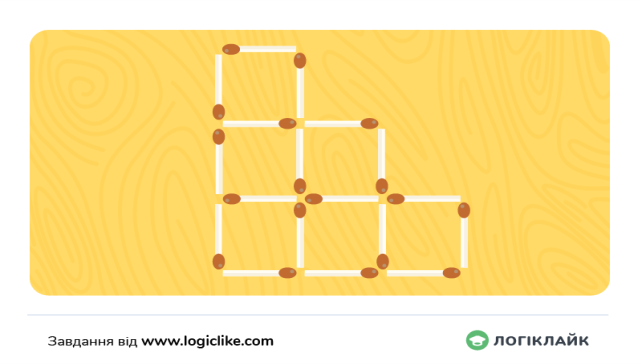
Приберіть 3 сірники так, щоб залишилися тільки 3 трикутники.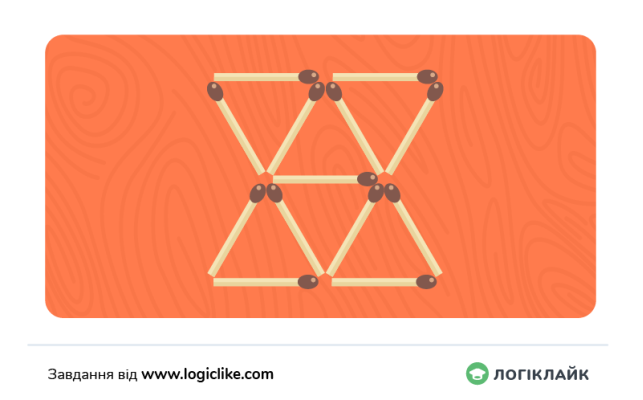

              Завдання з утворенням різноманітних фігур  

    Переклавши усього 2 сірники, побудуйте хатинку в дзеркальному зображенні до оригіналу. 

               

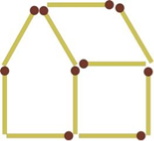
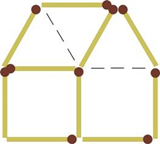
                                              Відповідь: 

 

      Перекладіть 3 сірники так, щоб з початкової конструкції утворилося 3 квадрати

            

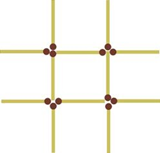
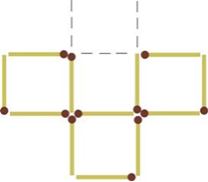
                                       Відповідь: 

 

      Приберіть 8 сірників таким чином, щоб залишилося всього 2 квадрата.

              

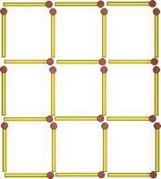
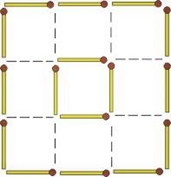
                                            Відповідь:

     Перекладіть 3 сірники таким чином, щоб рибка попливла у зворотній бік.

                     

                                                 Відповідь:  

      Покладіть сірники таким чином, щоб кожен з 6 сірників торкався інших 5.

        Відповідь:
 

 

  

 

         Завдання з утворенням цифр і чисел з сірників

   1. До трьох додайте ще 2 сірники таким чином, щоб утворилося вісім.

         

                                                                Відповідь: 

      2. Відомо, що довжина кожного сірника 4,5 см. Складіть з 13 сірників 1 метр. 

       Відповідь:

 

     3. Рівняння 3 х 3 + 1 = 9 невірне. Перенесіть всього 1 сірник таким чином, щоб рівняння стало вірним.

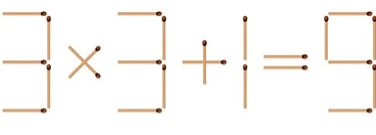
        Відповідь:

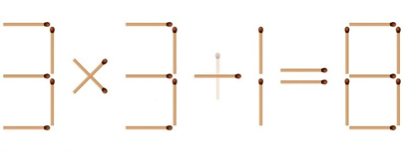
     Сірники, звісно, не іграшки, але не тоді, коли йдеться про захопливі творчі завдання! Виконання подібних вправ під час уроків дозволить учням переключити увагу, сконцентруватися та відчути радість маленької особистої перемоги.

 

 

 

 

Додаток № 4

 

 

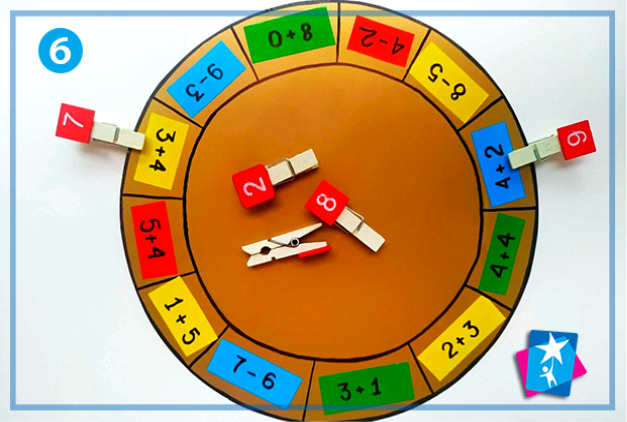
Що ? Де ? Коли ?

( Інтелектуальна  гра для учнів 7 – 9 класів )

 

Гра «Вікторина» №2

Тема: натуральні числа

Мета гри: систематизувати й узагальнити знання учнів про читання і запис, порівняння і зображення натуральних чисел на координатному промені.

Як бджілки з кожної квітки несуть свій узяток до вулика, так і учні своїй команді приносять бали з кожного завдання.

• Що таке натуральний ряд чисел?
• Чи існує найменше натуральне число? Назвіть його.
• Чи існує найбільше натуральне число? Чому? (Бо за кожним натуральним числом йде наступне більше число)
• Чи належить до натурального ряду число нуль?
•  Як називається система натуральних чисел?
•  Що означає нуль у розряді числа?
•  Який клас йде за класом мільйонів?
•  Назвіть найбільше восьмицифрове число.
•  Яке число йде за 99 999 999 ?
•  Назвіть найменше десятицифрове число.
•  Яке число передує 1 000 000 000?
•  Що таке відрізок? Як його позначають?
•  Що називають променем?
•  Як можна перенести відрізок в інше місце?
•  Що таке координатний промінь?
•  Як побудувати на координатному промені точку, що відповідає даному числу?
•  Як за допомогою координатного променя порівняти два числа?
•  Як порівняти два числа, які мають однакову кількість цифр?

 

 

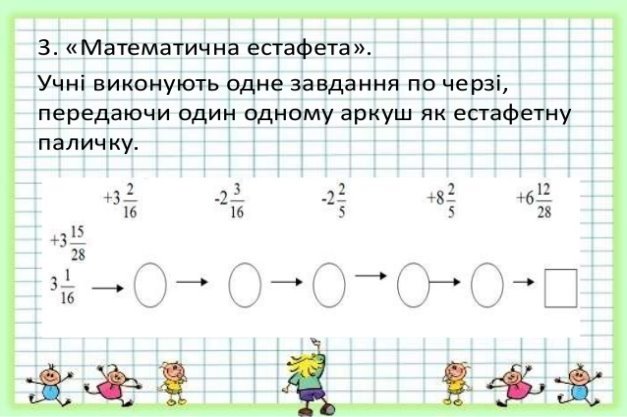
Естафета

Тема: порівняння натуральних чисел

Мета: закріпити знання правил порівняння натуральних чисел; відпрацювати навички застосування правила порівняння чисел, а також використання для цього властивостей координатного променя; сформувати вміння робити відповідні символічні записи порівняння чисел.

Обладнання: картки із завданнями.

Клас поділяється на команди (по рядах). Від кожної команди виділяється один представник — арбітр. Він стежить за роботою учнів іншої команди. Викликаються до дошки перші учні кожної з команд. їм вручаються «естафетні палички» — картки із завданнями. Учень розв'язує вправу, передає естафету іншому і сідає на місце. Арбітр стежить за правильністю розв'язання вправ. У випадку помилки повертає учня для повторного розв'язування.

Учні на місцях записують усі вправи своєї команди.

Виграє команда, яка першою і з найменшою кількістю помилок виконала всі завдання.

Підбивається підсумок гри. Визначається команда-переможець.

Зразки завдань:

Для першого ряду

1.               Накресліть координатний промінь і позначте на ньому точку, віддалену від точки А(12) на 5 одиничних відрізків.
2.               Яке з наведених чисел 70070, 70770, 70707, 70007 розташоване   на координатному промені праворуч від інших?
3.               Порівняйте числа:

а) 8 304 і 8 403;   б) 40 569 і 40 659;

в) 99 001 і 10 999.

 Назвіть усі натуральні числа, які більші за 465 і менші від 471.

 Запишіть цифру, яку можна підставити замість зірочки, щоб утворилася правильна нерівність (розгляньте всі можливі випадки):

        а) 46*7<4657;   6) 432*  <4326.

6. Яку з наведених цифр 5, 4, 3, 2 треба поставити замість кожної зірочки, щоб нерівність *3*4>4*3* була правильною?

1.                                                            Запишіть натуральні розв'язки нерівності:

                  а) х<5;    б) 4<х<10.

1.               Порівняйте значення виразів:

        а) 347-48  і   347+2;  б) 64-5-250   і    (18+17)-2.

9. Порівняйте:

а) 7 384 м  і 8 км; б) 5 ц і 329 кг;

в) 3 т 345 кг   і   34 ц і 45 кг.

Для другого ряду

 Накресліть координатний промінь і позначте на ньому точку, віддалену від точки М(10) на 4 одиничних відрізки.

 Яке з наведених чисел 5 500,5 050, 5 005,5055 розташоване на координатному промені ліворуч від інших?

1.               Порівняйте числа:

а) 7 640 і 7 700;   б) 23 045 і 23 049;

в) 102 319 і 99 999.

1.               Назвіть усі натуральні числа, які менші від 876 і більші від 870.

 Запишіть цифру, яку можна підставити замість зірочки, щоб утворилася правильна нерівність (розгляньте всі можливі випадки):

          а) 384*  >3847;      б) 10*23<10323.

6. Яку з наведених цифр 6, 1,3,4 слід поставити замість кожної зірочки, щоб нерівність 5 **2<5 * 2* була правильною?

1.                                                             Запишіть натуральні розв'язки нерівності:

                 а) х<6;     б) 8<х<11.

1.                  Порівняйте значення виразів:

          а) 485+67  і   485-33; б) (543+57):12    і   120∙2-190.

9. Порівняйте:

а) 8 км 23 м  і 8 230 м; б) 1326 кг  і 13 ц б кг;

в) 19 т    і 182 ц.

Для третього ряду

 Накресліть координатний промінь і позначте на ньому точку, віддалену від точки Р(9) на 6 одиничних відрізків.

 Яке із наведених чисел 40 404, 44 004, 40 440, 44 400 розташоване на координатному промені праворуч від інших?

1.               Порівняйте числа:

а) 8 065  і   8 712;   б) 30 243   і    30 199;

в) 93 998    і   89 999.

  Назвіть всі натуральні числа, які більші за 1009 і менші від 1014.

1.               Запишіть цифру, яку можна підставити замість зірочки, щоб утворилася правильна нерівність (розгляньте всі можливі випадки):

        а)18*43 > 18743;  б)397*  < 3975.

6. Яку з наведених цифр 8, 1, 4, 6 слід поставити замість кожної зірочки, щоб нерівність**99>*8*6 була правильною?

Запишіть натуральні розв'язки нерівності:

               а) х<8;          б) 3<х<6.

 Порівняйте значення виразів:

           а) 1040-948   і 1040-545; б) 223+24-6   і    402-21-2

9. Порівняйте:

а) 35 ц і 351 кг;  б) 45 т  і   45 000 кг;

в) 7235 м   і  7км 36м

 

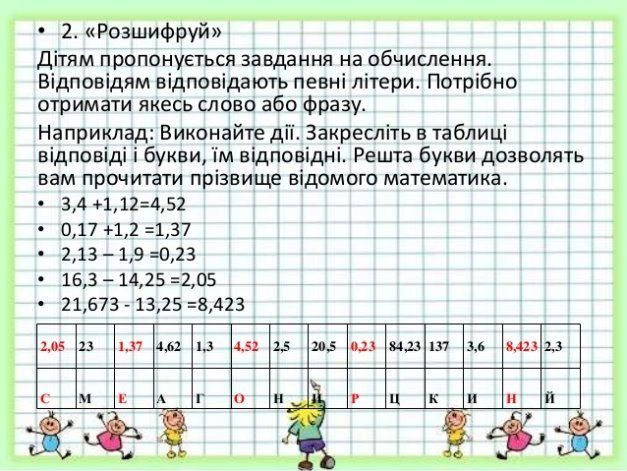
Гра «Ромашка»

   

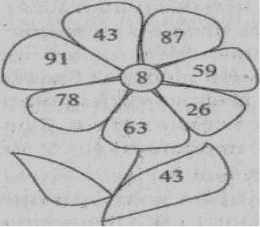
           Тема: усне додавання і віднімання

Мета гри: формувати навички усних обчислень.

Учитель вивішує таблицю або відкриває раніше закриту частину дошки.

До кожного з чисел, записаних на пелюстках, додати число, записане в центральному колі. Від кожного з чисел, записаних на пелюстках, відняти число, записане на листочку. Учитель послідовно показує на пелюстку, учні обчислюють усно і підносять руки. Вчитель викликає відповідаючого.

Гра «Хто швидше?»

Тема: додавання і віднімання натуральних чисел

Мета: формувати вміння учнів використовувати властивості додавання і віднімання під час виконання обчислень.

Команди одержують по чистому аркушеві. На ньому послідовно розв'язують завдання.

Завдання для гри

1. Обчисліть найзручнішим способом:

а) 78-(29+38);   б) 83-03-14);
в) 55-(35+17);   г) 874-(174+50);   
д) 701-(38+201);                є) 432-475+32);
ж) 894-(250+294);            з) 488-(388-80);

і) 808-(550-92).

 У виразі 20 - (15 - х)  число х набуває таких значень: 0, 1, 5, 10,  15. При якому з них значення даного виразу буде найбільшим?

 Поставте замість зірочок знаки «+», «—» так, щоб виконувалися рівності:

 а) 40*20*60*30*50=100; б) 80*10*70*50*90=100.

Розв'язавши завдання, учень передає аркуш наступному і працює в зошиті. Команда, яка перша і без помилок виконала завдання на аркуші, одержує 20 балів мінус число учнів, що не закінчили розв'язування вправи в зошиті.

Інші команди одержують кількість балів, що дорівнює числу розв'язаних на аркуші завдань мінус число учнів, що не закінчили розв'язування вправи в зошиті.

Самостійне розв'язування вправи 2. Учень, який виконав завдання першим, приносить команді один бал.

Вправа 3. Пропонується вгадати відповідь, не розв'язуючи. Дається три спроби. Вдала спроба приносить команді 3 бали. Письмове розв'язування вправи. Учень, що виконав завдання першим, приносить команді 1 бал.

Визначення команди-переможниці за кількістю набраних балів.

 

Гра «Математичний волейбол»

Тема: числові і буквенні формули. Вирази

Мета гри: закріпити знання учнів про основні поняття теми (числові і буквені вирази, формули, значення числового виразу); продовжувати формувати навички складання і обчислення значень буквених виразів.

Клас поділяється на дві приблизно рівні за силою команди (можливо, за варіантами).

Обирається суддя, який стежить за часом і, можливо, його помічник, який стежить за рахунком (записує рахунок на дошці).

Починає перша команда. Подача — це запитання з теоретичного матеріалу або вправа на усне обчислення. Вона адресується конкретному гравцеві другої команди. Протягом встановленого часу цей гравець повинен або перепасувати запитання іншому гравцеві своєї команди, назвавши його прізвище (перепасовка дозволяється лише один раз), або відбити, відповівши на запитання, після чого посилає аналогічне завдання гравцеві іншої команди. Якщо відповідь неправильна чи несвоєчасна, то команді забито м'яч.

Якщо запитання повторене чи не стосується теми, неправильно сформульоване, відбувається втрата подачі. Подача переходить до команди суперників.

Гра продовжується до вказаної кількості забитих м'ячів або обумовлений час, після чого визначається команда-переможниця і оцінюються кращі гравці.

Завдання гри

•     Знайдіть суму, різницю, добуток і частку чисел 20 і 5.
•                 Суму чисел 13 і 17 збільшіть у 5 разів.

3. Різницю чисел 72 і 46 збільшіть на 14.

1.                                                                       Чому дорівнює значення виразу Зх-8, якщо:

  1) х=9;  2) х=0.

1.Обчисліть значення у за формулою у = х ∙ х + 13, якщо:

  1) х=1;  2) х=10.

6. Два равлики повзуть зі швидкістю 5 м/хв і 3 м/хв. З якою швидкістю вони віддаляються один від одного, якщо:

1)  повзуть в одному напрямку;

2) повзуть назустріч один одному?

7. Перевірте, чи правильна нерівність

1896 - (635 + 458) <  2400 - (1729 - 123).

8. У залі для глядачів т рядів, а в кожному ряду на 5 місць більше, ніж кількість рядів. Скільки місць у залі для глядачів. Складіть вираз для розв'язування задачі, знайдіть його значення, якщо т = 15; 20.

9. Знайдіть значення виразу, обираючи зручний порядок обчислень:
                   1) (524 + 397) - 224;  2) 877 – (77 +216);

3) (325 + 419) + 675;  4) 631 + 308 + 1369 + 629.

10. Спростіть вирази:

1) (63 + х) + 29;   2) а + 614 + 235;

3) (22 + а) - 7;   4) 69 - (m + 12).

11.  На першій зупинці з автобуса вийшло 11 пасажирів, а увійшло  - 6. На другій зупинці вийшло 8, а увійшло 15 пасажирів. Скільки пасажирів було в автобусі до першої зупинки, якщо після другої зупинки їх стало 30?

Гра «Індивідуальне лото»

Тема: рівняння

Мета гри: закріпити навички учнів застосовувати набуті знання під час розв'язування рівнянь.

У спеціальному конверті учням пропонується набір карток. Зазвичай їх більше, ніж відповідей на великій картці, яку також вкладено в конверт. Наприклад, на великій карті намальовано 6 прямокутників, а в учня 7—8 карток таких самих розмірів, що й записані на них вправи. Учень дістає з конверта картку, розв'язує рівняння і накриває нею відповідний результат. Картки накладають лицьовим боком униз. Якщо всі рівняння розв'язані правильно, то зворотні боки карток, що накладені на велику картку, складають якийсь умовний шифр: рисунок, креслення, літеру. Вчитель, проходячи по рядах, легко визначає результати роботи учнів. За бажанням роботу учнів можна оцінити.

Зразок завдань для гри «Математичне лото»

20 + x = 70;                   

42 – х   =  7;

у - 60 = 31;

(48 - х) + 24 = 63;

516 -(у + 145) = 276;

(у + 83) -112 = 243;

Якщо до числа а додати 13, то сума буде на 27 менша за 50.  Знайдіть а.

Знайти значення змінної х, при якому рівність буде правильною 8 + 14 ∙ 8  = 10 ∙ x

Велика картка

272	9	50	91
10	12	35	55

 

Гра-естафета «Знайди помилку!»

Тема: сполучна і розподільна властивість множення.

Мета гри: закріпити навички виконувати множення величин із застосуванням сполучної та розподільної властивостей множення.

На дошку проектується або відкривається заздалегідь заготовлений рисунок.

Клас поділяється на команди за кількістю рядів.

До дошки виходять учні по одному від кожної команди, знаходять число, що є результатом виконаного завдання. Перше завдання записано у першому прямокутнику. Знайшовши потрібне число, учень проводить стрілку від цього прямокутника до знайденого числа і сідає на місце, передаючи естафету (крейду) наступному члену команди, той шукає відповідь вправи, записаної в прямокутнику, під яким стоїть число, до якого підведена стрілка, проводить нову стрілку, передає естафету далі і так до кінця польоту.

По одному учню від кожної команди — контролери. Вони перевіряють правильність маршруту іншої команди, у випадку помилки повертають учня, примушуючи його переробити завдання.

Команда, яка закінчує роботу першою і правильно, одержує 12 балів. Інші одержують по закінченню роботи стільки балів, скільки вправ було розв'язано під час польоту першої команди.