Методичні рекомендиції з "Інженерної графіки" щодо винонання графічной роботи "Перетин геометричних тіл площиною"

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНА МЕТАЛУРГІЙНА АКАДЕМІЯ УКРАЇНИ

КРИВОРІЗЬКИЙ ТЕХНІКУМ

 

 

 

 

МЕТОДИЧНІ ВКАЗІВКИ

 

ЩОДО ВИКОНАННЯ ГРАФІЧНОЇ РОБОТИ

 «ПЕРЕТИН ГЕОМЕТРИЧНИХ ТІЛ ПЛОЩИНОЮ»

 

     дисципліни  НАРИСНА ГЕОМЕТРІЯ ТА ІНЖЕНЕРНА ГРАФІКА

     для студентів 2 курсу усіх спеціальностей

        

             

                                                           Розробник: викладач  Коч О.Д.                                                                

                                                                    

                                                            Розглянуто і схвалено на засіданні                                          

                                                           циклової комісії  загально технічних 

                                                           та механічних  дисциплін

                                                           Протокол №____від _______2017 р.

                                                           Голова циклової комісії:

                                                                ____________О.М. Гавриш

 

 

м. Кривий Ріг

2017 рік

1. Загальні положення.

 

 

При перерізі багатогранника площиною утворюється багатокутник, який лежить у січній площині. Вершини багатокутника – це точки перетину ребер багатокутника, а  сторони – лінії перетину його граней із січною площиною.

Кожна задача на переріз геометричного тіла площиною складається з розв’язання комплексу таких питань:

а)  побудова проекцій фігури перерізу.

б) визначення натуральної величини фігури перерізу.

в) побудова розгортки зрізаного тіла.

г) побудова аксонометричного зображення.

 

2. Перетин призми і піраміди.

 

Залежно від січної площини в перерізі призми можуть утворитися такі фігури:

а) багатокутник, паралельний і рівний основі, якщо січна площина паралельна основі (рис. 1 а).

б) прямокутник при прямій призмі або паралелограм при похилій, якщо площина паралельна ребрам призми (рис. 1 б).

в) багатокутник, не рівний і не подібний до основи, якщо січна площина нахилена до ребер призми (рис. 1 в).

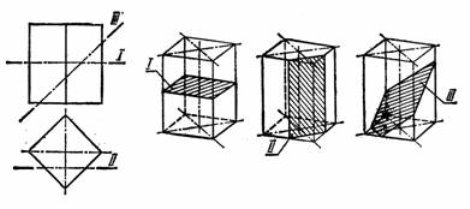
                                   а)                         б)                     в)

            Рис.1

 

 

“Перетин призми площиною. ”

 

    Графічна послідовність виконання завдання:

 

    1. Згідно вихідних даних варіанту побудувати комплексне креслення

правильної шестикутної призми з фронтально проектуючою січною

площиною (рис. 2  а).

2. Щоб побудувати комплексне креслення зрізаної призми, необхідно

на фронтальній проекції позначити точки перетину січної площини з 

ребрами призми. Знайти горизонтальну і профільну проекцію цих 

точок. З’єднавши проекції цих точок  отримаємо фігури перерізу 

призми, які  слід заштрихувати (рис. 2 б).

 

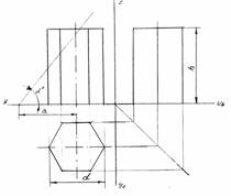
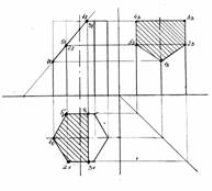
а)                                                          б)

Рис. 2

     3.  Для побудови розгортки необхідна натуральна величина  фігури перерізу,яку  знаходимо способом заміни площин проекцій. Площину П₂ замінюють на площину П_4. Вісь х₁ нової системи П₂ /П проводять паралельно фронтальній проекції фігури перерізу. З точок 1₂; 2₂; 3₂; 4_2;  5 ₂ ; проводять перпендикуляри до осі  х₁ . Точки 1₄; 2₄; 3₄; 4₄; 5₄;  будують  відложивши  координати  у проекцій точок 1₁; 2₁; 3₁; 4_1; 5_1.  З’єднують проекції точок 1₄; 2₄; 3₄; 4₄; 5₄;  окреслена  фігура – натуральна величина перерізу (рис. 3).

 

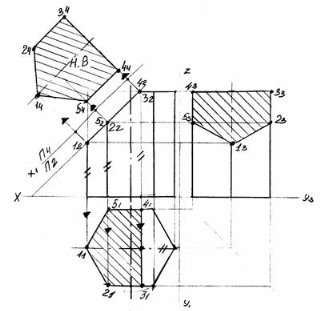
Рис. 3

     4. Розгортка бічної поверхні шестикутної призми це шість

прямокутників, висота яких дорівнює висоті призми, а ширина - стороні  її основи. На ребрах розгортки призми відкладають точки 1, 2, 3, 4, 5,  узявши їх висоти  з фронтальної проекції  призми,  тобто   1= z1₂ ; 2= z2₂;……. і т.д. До лінії перерізу  добудовують натуральну величину перерізу і частину не зрізаної верхньої основи, нижня  основа призми залишається без змін.  Лінії згину розгортки  зображують штрих - пунктирною з двома крапками (рис. 4). 

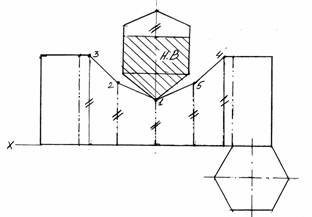
Рис. 4

 

5. Аксонометричне зображення призми будують в прямокутній 

 ізометрії. Будують осі, на  яких  відкладають  нижню  основу  призми – правильний шестикутник. З вершин  шестикутника ставлять перпендикуляри , на яких відкладають точки 1= z₁; ..... 5=z₅; і т. д.  З’єднавши  ці точки  отримаємо аксонометричне  зображення зрізаної призми (рис. 5).

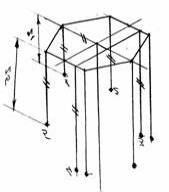
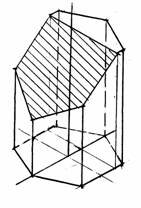
Рис. 5

 

“Перетин піраміди площиною. ”

 

Графічна послідовність виконання завдання:

 

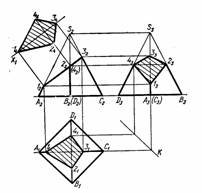
    1.  Задано правильну чотирикутну піраміду. Діаметр кола, в яке вписаний правильний чотирикутник дорівнює d, висота піраміди дорівнює h. Піраміда зрізана  фронтально проектуючою  площиною  (рис. 6 а).

    2.  Побудова проекцій фігури перерізу. Слід фронтально проектуючої 

площини перетнеться з ребрами піраміди в точках 1₂; 2₂; 3₂; 4₂.  Знаходимо горизонтальну і профільну проекцію цих точок.Пряма  ламана лінія окреслить фігуру перерізу на горизонтальній і профільній проекціях  піраміди. Натуральну величину цієї фігури знаходимо  методом  заміни площин проекцій (рис. 6 б).

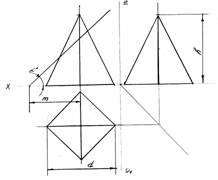
а)                                       б)

Рис. 6

     3.  Розгортка піраміди. Спочатку будують повну розгортку бічної  поверхні. Для цього з точки S радіусом R = S₂A₂  проводимо дугу, на якій відкладають величину ребер основи АВ=А₁В₁; ВС = В₁С₁; і т . д. Точки А, В, С, D, з’єднуємо з вершиною S отримаємо бічні  ребра піраміди, на яких відкладаємо точки 1 = А₂ 1₂; 2 = В₃ 2₃; 3 = С₂ 3₂; 4 = D₃ 4₃. Натуральну величину фігури  перерізу  добудовуємо одним із способів побудови подібних багатокутників. Нижня  основа піраміди  залишається  незмінною  (рис. 7).

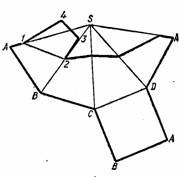
Рис. 7

4. Побудова аксонометричного зображення виконуємо в

 прямокутній  диметрії. На осях х- у будуємо нижню основу  піраміди по осі z  відкладають її висоту з’єднуємо  ребра основи  з висотою S. На ребрах  піраміди координатним способом  відкладають точки 1; 2; 3; 4 (рис. 8 а). З’єднуємо  ці точки  замкненою ламаною лінією. Наводимо видимі елементи  основною  суцільною лінією,  невидимі  штриховою (рис 8 б).   

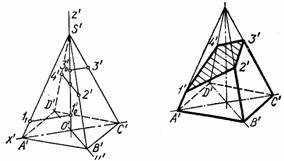
а)                                  б)

Рис. 8

 

3. Перетин циліндра.

 

     У перерізі прямого кругового циліндра  площиною можуть  утворитися такі фігури:

а) прямокутник, якщо площина перерізу паралельна осі циліндра

 (рис. 9а);

б) коло, якщо площина перпендикулярна до осі (рис. 9 б);

в) еліпс, якщо площина нахилена до осі (рис.9 в), причому еліпс буде повний, якщо площина перетинає всі твірні циліндра, і неповний, якщо  площина перетинає одну або обидві основи циліндра.  

 

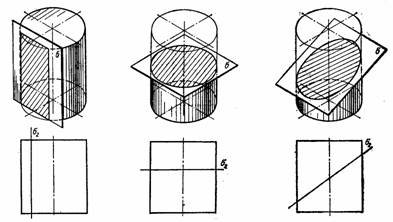
а)                         б)                         в)

Рис. 9

 

 

 

“Перетин циліндра площиною. ”

 

Графічна послідовність виконання завдання:

 

1. Згідно вихідних варіанту побудувати три проекції повного  циліндра зрізаного фронтально проектуючою  площиною  (рис. 10). 

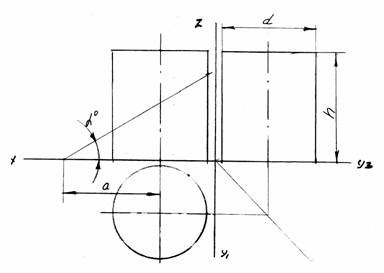
Рис. 10

 

     2. Коло нижньої основи (горизонтальну проекцію) поділити на вісім

рівних частин. Точки поділу 1₁;2₁... 8₁  є одночасно горизонтальними проекціями твірних  циліндра.  Керуючись  цими точками,  будуємо фронтальні і профільні проекції твірних. Натуральну величину фігури перерізу   знаходимо  способом заміни площин  проекцій  (рис. 11).

  

   3.  Розгорткою бічної поверхні циліндра є прямокутник, висота якого

дорівнює висоті циліндра, а довжина – довжині  розгорнутого кола - його основи (d). Довгу сторону прямокутника ділимо на вісім рівних частин і з точок поділу проводимо твірні. На цих твірних  відкладаємо  точки відстань до яких виміряємо  на фронтальній проекції. Наприклад  1 = z1₂;  2 = z2₂;...... і т. д. Отримані точки з’єднують  за допомогою   лекала. До цієї лінії добудовують натуральну величину фігури  перерізу. Нижня основа конуса  залишається  без  змін   (рис. 12)

 

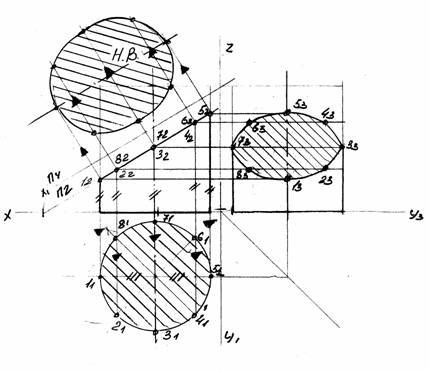
Рис. 11

 

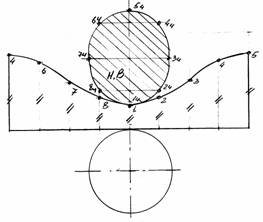
Рис. 12

 

 

 

     4.  Ізометрична проекція циліндра, розсіченого площиною. Коло нижньої основи циліндра зображується у вигляді еліпса, який 

замінюємо на чотирьох центровий овал. Використовуючи координати х₂ і х₄   проводимо твірні циліндра, на яких відкладаємо точки 1 = z1₂; 

2 = z2₂;….. і т. д.  Знайдені  точки перерізу  з’єднуємо  за допомогою лекала (рис. 13).      

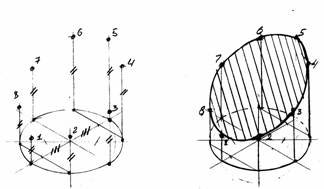
Рис. 13

 

 

4. Перетин конуса.
5.  

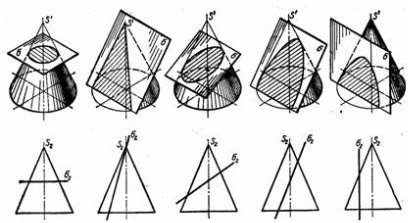
Залежно від напрямку січної площини в перерізі конуса можуть утворюватись:

а)   коло, якщо січна площина паралельна основі конуса   (рис. 14 а);

б)  трикутник, якщо січна площина проходить через вершину конуса (рис. 14 б);

в)  еліпс повний або неповний, якщо січна площина нахилена до осі

під кутом, більшим закут нахилу твірної до осі  (рис. 14 в). Неповний 

еліпс утвориться в тому разі, коли січна площина перетне основу  конуса;

г)  парабола, якщо січна площина паралельна твірній конуса, тобто

нахилена до осі конуса під кутом, що дорівнює куту нахилу  твірної до осі (рис. 14 г), і не проходить через вершину;

д) гіпербола, якщо січна площина паралельна двом твірним або осі

конуса. Тобто тоді, коли ця площина нахилена до осі конуса під  кутом меншим за кут нахилу твірної до осі, і не проходить через вершину (рис. 14 д)

 

а)             б)              в)            г)             д)

Рис. 14

 

“Перетин конуса площиною. ”

Графічна послідовність виконання завдання:

1. Спочатку креслимо три проекції повного конуса і слід січної

площини. Коло основи поділяємо на вісім рівних частин із точок

поділу проводимо горизонтальні проекції прямих A₁S₁,   B₁S₁  і т.д. конуса. За цими проекціями будуємо фронтальну проекцію твірних, 

які перетнуться  із слідом січної площини. В точках  перетину ми  отримаємо проекції точок 1_{2 ,}2_2,  3₂, ... і т.д. (рис.15).

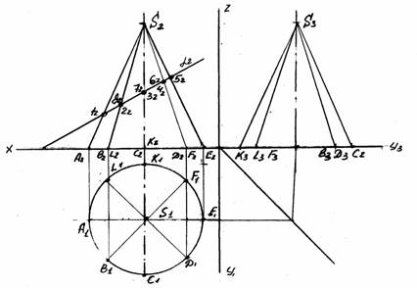
Рис. 15

 

2. Для побудови фігури перерізу на горизонтальній і профільній

 площині проекцій знаходимо горизонтальну і профільну проекцію

 цих точок. За допомогою лекал з’єднуємо ці точки плавною кривою. Натуральну величину фігури перерізу знаходимо способом заміни 

площин проекцій (рис.16).

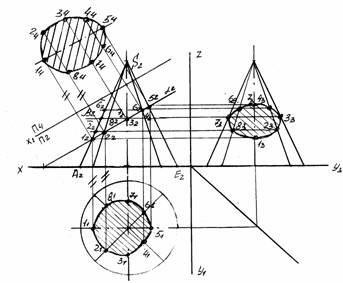
Рис. 16

   3. Розгортка конуса. Розгорткою бічної поверхні конуса є сектор круга, радіус дуги якого дорівнює твірній конуса, а довжина дуги –довжині кола -  основи конуса. Центральний сектор визначається за формулою  = r/ l 360, де r –  радіус кола основи, а l – довжина твірної конуса. Дугу розгортки поділяємо  на вісім рівних  частин і проводимо твірні конуса. На кожній твірній відкладають  точки,  які дорівнюють  S1 = S₂1₂; S2 =S₂2₂ ... і т. д (рис. 17).

    4. Побудову аксонометричного зображення зрізаного конуса    починають з побудови   ізометрії повного конуса (рис.18 а).

Використовуючи  координати х відкладаємо точки 1₀, 2₀ ... і т. д.   З цих точок ставимо перпендикуляри на яких відкладаємо координати z _1…z_5. Через отримані точки 1,2,..і т. д  проводимо лінії паралельні  осі у, на яких відкладають точки 2 = 2₁, 3 = 3₁...і т.д.  Отримані точки з’єднують за допомогою лекал (рис.18 б).

 

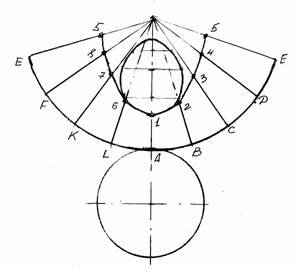
Рис. 17

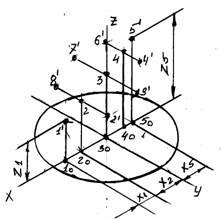
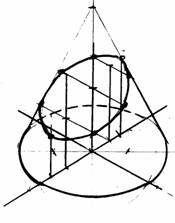
а)                                                     б)

Рис. 18

 

 

 

 

 

 

 

 

 

 

Питання для самоконтролю.

 

1.    Які криві можуть утворитися в перерізі прямого    конуса різними площинами?

2.   Як побудувати розгортку зрізаного конуса? Зрізаного

     циліндра?

3.   Які фігури можуть утворитися в перерізі призми різними 

     площинами?

4.   Які криві можуть утворитися в перерізі циліндра різними 

     площинами?

5.   Як визначити центральний сектор розгортки конуса?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

     Методичні вказівки щодо виконання  графічної роботи «Перетин геометричних тіл площиною» дисципліни „Нарисна геометрія та інженерна графіка “   складені на основі галузевого  стандарту підготовки молодшого спеціаліста і  навчального плану для студентів 2 курсу денного та 1 курсу  заочного відділень  усіх спеціальностей. 

 

Укладач  ______________О.Д. Коч  викладач першої категорії.

                  

 

Методичні вказівки щодо виконання  графічної роботи «Перетин геометричних тіл площиною»   обговорено і схвалено на засіданні циклової комісії загальнотехнічних  та механічних дисциплін

 

Протокол № ____  від  „____“  _________2017р.

Голова циклової комісії

_________  О.М. Гавриш

„ _____ “ _________2017  р.