Методичні вказівки щодо проведення лабораторної роботи "Дослідження циклічного коду Грея"

Дисципліна: «Основи теорії кодування та передавання інформації»

 

 

МЕТОДИЧНІ  ВКАЗІВКИ ЩОДО ПРОВЕДЕННЯ  ЛАБОРАТОРНОЇ РОБОТИ

 

"Дослідження циклічного коду Грея"

 

    Мета роботи: вивчити циклічний код Грея, з'ясувати особливості його побудови і застосування.

 

Короткі теоретичні відомості

 

Іноді буває необхідним, щоб лексикографічно (тобто за алфавітом або по зростанню) упорядковані символи при двійковому кодуванні різнилися мінімальною кількістю розрядів. Коди, що задовольняють цій умові, називаються кодами Грея або однокроковими кодами .

Часто в цифровій техніці потрібна для числового коду схема кодування, відповідно до якої при переході від одного числа до наступного змінювалася б тільки одна цифра. Виконання цієї умови необхідно, коли внаслідок технічних неточностей момент перемикання не може бути точно витриманий. При перемиканні двох чисел через це можуть виникнути неправильні комутаційні операції. Як приклад подібної помилки розглянемо перемикання від 1₁₀ до 2₁₀ в двійковому коді (див. рисунок 1):

 

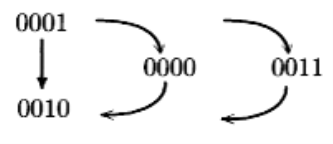
Рисунок 1 - Перемикання від 1₁₀ до 2₁₀ в двійковому коді

 

При цьому перемиканні змінюються біти 0 і 1 при одночасному перемиканні безпосередньо досягається нове число. Якщо спочатку змінюється біт 0, то з'являється число 0000 і тільки коли змінюється біт 1, отримуємо правильне число 0010. Якщо ж спочатку змінюється біт 1 і потім змінюється біт 0, то в проміжку виникає число 0010. Коди Грея дозволяють уникнути цієї дуже серйозної помилки за рахунок того, що при переході від одного кодового слова до наступного змінюється тільки один розряд.

Код Грея — одна із систем кодування інформації, в якій два послідовні коди відрізняються значенням лише одного біта.

 

 

 

 

 

Коди Грея одержали свою назву по ім'ю Франка Грея (Frank Gray), фізика з Bell Telephone Laboratorіes, що в 1930-х роках винайшов метод, який у цей час використовується для передачі кольорового телевізійного сигналу, разом з існуючими методами передачі й одержання чорно-білого сигналу; тобто при одержанні кольорового сигналу чорно-білим приймачем зображення виводиться відтінками сірого кольору. Працюючи в Bell Laboratorіes, Фрэнк Грей брав участь у перших днях цифрової революції.

 

 

 

Використання кодів Грея засновано насамперед на тому, що він мінімізує ефект помилок при перетворенні аналогових сигналів у цифрові (наприклад, у багатьох видах датчиків).

Коди Грея часто застосовуються в датчиках-енкодерах (див. рисунок 2). Їх використання зручно тим, що два сусідніх значення шкали сигналу відрізняються лише в одному розряді.       Вказану властивість використовують для збільшення надійності роботи системи оптичних фотодіодів при встановленні кута повороту дисків-носіїв інформації.

 

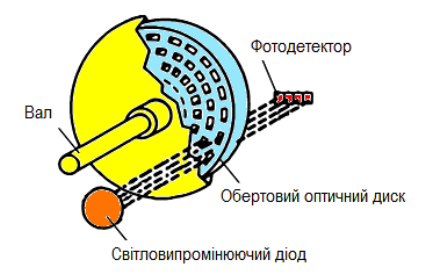
Рисунок 2 - Датчик-енкодер на коді Грея

 

Оптичний диск з кодом Грея забезпечує визначення точного положення вала в кожен момент часу; відсутність помилок при запуску системи та підрахунку імпульсів на кордонах; можливість визначити напрямок обертання; відсутність проблем з граничними положеннями, тому що змінюється одночасно не більше одного біта.

Також коди Грея використовуються для кодування номерів доріжок в твердих дисках накопичувачів інформації.

Код Грея можна використовувати для вирішення задачі про «Ханойські вежі».

Широко застосовуються коди Грея і в теорії генетичних алгоритмів для кодування генетичних ознак, які представлені цілими числами.

Код Грея використовується для генерації сполучень методом «обертових дверей».

Перетворення двійкового простого коду на код Грея виконується за алгоритмом:

 

де у_і -  значення і-го розряду коду Грея;

– відповідні значення розрядів двійкового числа (і = 1, 2 … , починаючи справа).

У таблиці 1 наведені значення коду Грея для десяткових цифр (для порівняння також зазначені їхні прямі коди, значення якого теж упорядковані).

 

  Таблиця 1

Цифра	Прямий код	Код Грея
0	0000	0000
1	0001	0001
2	0010	0011
3	0011	0010
4	0100	0110
5	0101	0111
6	0110	0101
7	0111	0100
8	1000	1100
9	1001	1101

 

Таким чином, для утворення комбінації коду Грея практично досить зсунути двійкову комбінацію простого коду на один розряд ліворуч, порозрядно додати її за модулем два до початкової кодової комбінації без перенесенням між розрядами і відкинути молодший розряд здобутої суми.

Як видно, коди лексикографічно упорядкованих цифр 1 і 2 у випадку коду Грея різняться одним двійковим розрядом, а прямі коди цих же цифр - двома розрядами. Аналогічну картину можна спостерігати у випадку пар цифр 3 і 4; 5 і 6; 7 і 8.

Код Грея  є рефлексним кодом. Свою назву рефлексні коди дістали через наявність осей симетрії, відносно яких виразно проглядається ідентичність елементів у деяких розрядах.

 

Для формування коду Грея можна використовувати наступну послідовність дій:

Крок 1: код Грея для цифр 0 і 1 дорівнює 00 і 01, відповідно.

Крок 2: для побудови кодів Грея для десяткових чисел 2 і 3 побудуємо таблицю 2, у якій для нумерації рядків і стовпців використані коди Грея для чисел 0 і 1:

 

 Таблиця 2

 

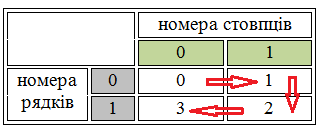
В осередках таблиці 2 розміщені кодуємі  десяткові числа, включаючи й уже закодовані 0 і 1. Стрілки показують напрямок переміщення по осередках для формування коду одного із чисел (саме число зазначене в осередку). Тоді код Грея для довільного числа, розміщеного в деякому осередку, формується як номер рядка й номер стовпця для цього осередку. Так, код Грея для числа 3 - це 10, а для числа 2 - 11.

Оскільки код Грея має постійну довжину, то сформовані раніше коди для чисел 0 і 1 поповнюються незначними нулями, тобто код Грея для 0 - це 000, а для 1 - це 001.

Крок 3: одержавши коди Грея для чотирьох десяткових чисел, використовуємо їх як  номери рядків і стовпців, щоб сформувати кодові комбінації для перших шістнадцяти десяткових цифр (див. таблицю 3):

 

    Таблиця 3

	00	01	11	10
00	0	1	2	3
01	7	6	5	4
11	8	9	10	11
10	15	14	13	12

 

Так, наприклад, для одержання коду числа 9 виписують позначення рядка й стовпця: відповідно, 11 і 01;. для числа 15 кодом буде комбінація 1000, для числа 11 - 1110 і т.д.

Оскільки перехід від числа 15 до 0 також є однокроковимим (ці числа мають коди, відповідно, 1000 і 0000), побудований код називають також циклічно однокроковим.

Особливістю коду Грея є те, що зміна елементів у кожному розряді при переході від комбінації до комбінації відбувається в два рази рідше, ніж у простому коді, завдяки чому значно спрощується кодер.

Крім того, при додаванні двох сусідніх комбінацій рефлексного коду за модулем 2 кількість одиниць дорівнюватиме кількості розрядів мінус 3, тобто одиниці, що використовується для перевірки правильності прийнятої кодової комбінації.

На рівні апаратної реалізації для перетворення комбінації простого N- розрядного двійкового коду в комбінацію коду Грея вимагає N-1 елементів ВИКЛЮЧАЮЧЕ АБО, з’єднаних відповідно рисунку 3.

 

 

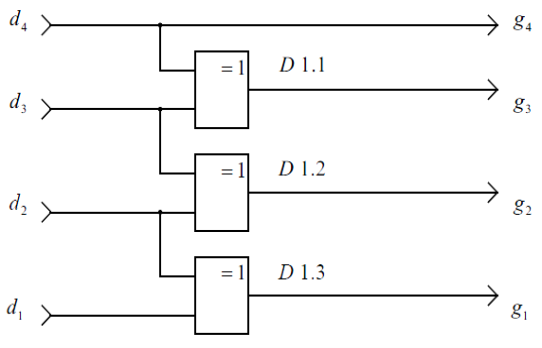
Рисунок 3 - Схема перетворення двійкової комбінації в комбінацію коду Грея

 

 

Порядок виконання роботи

 

1. Створіть у програмі  Multisim схему дослідження побудови коди Грея згідно рисунку 4.

2. Перетворіть комбінації простого двійкового коду в комбінації коду Грея.  Результати побудови   коду Грея занесіть в таблицю 4.

 

 

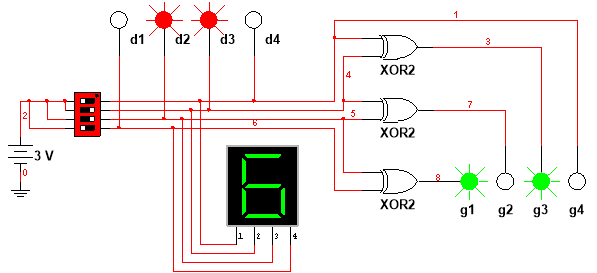
Рисунок 4 – Схема дослідження кодера Грея

 

 

Таблиця 3

Число	двійковий код					код Грея
	d1	d2	d3	d4		g1	g2	g3	g4
0	0	0	0	0
1	0	0	0	1
2	0	0	1	0
3	0	0	1	1
4	0	1	0	0
5	0	1	0	1
6	0	1	1	0
7	0	1	1	1
8	1	0	0	0
9	1	0	0	1
10	1	0	1	0
11	1	0	1	1
12	1	1	0	0
13	1	1	0	1
14	1	1	1	0
15	1	1	1	1

 

 

Зміст звіту лабораторної роботи

 

1.               Назва та ціль роботи.
2.               Схема дослідження коду Грея.
3.               Таблиця результатів досліду.
4.               Короткі висновки з роботи і  відповідь на контрольне питання.

 

 

Контрольне питання

 

1.               Які коди називаються кодами Грея?

 

 

Література

 

1.               Беркман Л.Н., Бондарчук А.П., Гайдур Г.І., Чумак Н.С. Кодування джерел інформації та каналів зв’язку :  навчальний посібник. – Київ: ННІТІ ДУТ, 2018.
2.               Фетюхіна Л. В. Теорія інформації та кодування : навч.-метод. посібник/ Л. В.Фетюхіна, О. А. Бутова – Харків: НТУ «ХПІ», 2012.