Методичні вказівки для виконання практичного заняття за темою: «Деформація розтягу та стиску»

Методичні вказівки

за темою: «Деформація розтягу та стиску»

Для студентів спеціальності

208 «Агроінженерія» ІІ курсу денної форми навчання

Викладач:  Лоїк О.А.

 

Ро́зтяг (стиск) або ро́зтяг-стиск— вид деформування твердого тіла, при якому його розміри вздовж однієї осі збільшуються (зменшуються) під дією сил, рівнодійна яких є перпендикулярною до поперечного перерізу тіла і проходить через центр його ваги .

Процеси, які відбуваються при розтягу або стиску здебільшого є ідентичними, як і механічні характеристики дуже великої кількості конструкційних матеріалів. Тому ці протилежні за напрямом види деформування — розтяг і стиск — описують одними й тими ж математичними залежностями й об'єднують їх в один вид: розтяг–стиск. При цьому домовилися: все, що стосується розтягу (сили, напруження, деформації тощо) вважати зі знаком «+», а те, що стосується стиску — зі знаком «–».

 

 

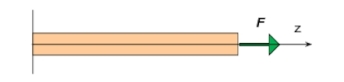
Якщо тіло розтягувати, то відстань міх шарами молекул збільшується, відповідно збільшується й розміри тіла. Таку деформацію зазнають троси, канати, ланцюги в піднімальних пристроях тощо.

 

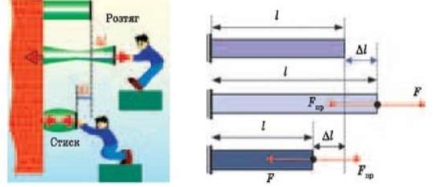
При розгляді розтягу–стиску користуються основними гіпотезами опору матеріалів. Крім того, вводять ще гіпотези, характерні саме для певних видів простої деформації. Наприклад, приймають гіпотезу плоских перерізів — поперечні перерізи стержня, плоскі до деформації, залишаються плоскими і після неї, переміщуючись поступально вздовж осі стержня.

Напруження при розтягу-стиску

У поперечному перерізі навантаженого зусиллями розтягнення стержня виникають лише нормальні складові внутрішніх сил — N. Тому в довільному поперечному перерізі можуть виникати лише нормальні напруження. Причому ці напруження в кожній точці перерізу будуть однаковими, оскільки маленькі частки (диференціал) сили dN будуть однаковими на елементарних площинках dA, тобто:

{\displaystyle \sigma ={\frac {dN}{dA}}={\frac {N}{A}},}

тоді критерій міцності при розтягу–стиску можна записати так:

або {\displaystyle \sigma _{max}={\frac {N}{A_{min}}}\leq [\sigma ],}

 

де {\displaystyle [\sigma ]} − це допустимий рівень напружень, який є однією з основних механічних характеристик конструкційного матеріалу.

 

Пружний розтяг-стиск

Експериментально встановлена залежність абсолютного видовження (Δl) від прикладеного зусилля (F) в умовах пружності:

{\displaystyle \Delta l={\frac {F\cdot l}{E\cdot A}},}

де E — модуль Юнга, МПа.

Ця ж залежність може бути виражена через відносну деформацію (ε) й напруження (σ):

{\displaystyle \varepsilon ={\frac {\Delta l}{l}}={\frac {F}{E\cdot A}}={\frac {\sigma }{E}}.}

Величину  {\displaystyle E\cdot A} називають жорсткістю стержня при розтягу-стиску,  він характеризує одночасно фізико-механічні властивості матеріалу і геометричні розміри поперечного перерізу бруса.

Для бруса, що має кілька ділянок, які відрізняються матеріалом, розмірами поперечного перерізу, величиною поздовжньої сили, зміна довжини всього бруса дорівнює алгебраїчній сумі видовжень і укорочень окремих ділянок:

.

Стержні, на які діють розтяжні або стискальні сили, як показали досліди, зазнають не тільки поздовжньої, а й поперечної деформації. Відносна поперечна деформація дорівнює:

,

де: d – початковий поперечний розмір,

   d – зміна поперечного розміру.

Залежність  між відносною поперечною  і відносною поздовжньою  деформаціями вперше встановив французький учений Пуассон (1781–1840).

коефіцієнт Пуассона, залежить від властивостей матеріалу і лежить у межах від 0 (корок) до 0,5 (парафін); для сталі = 0,25….0,33, для чавуна =0,23..0,27.

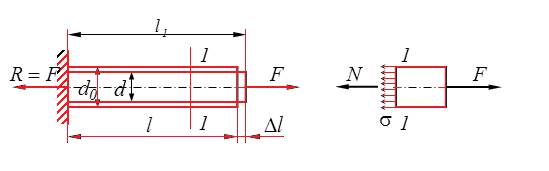
Розрахунки на міцність: перевірка міцності, визначення допустимого

навантаження, визначення необхідних розмірів поперечного перерізу

 

Умова міцності. Міцність стрижня під час осьового розтягу і стиску забезпечена, якщо для кожного його поперечного перерізу найбільше розрахун-кове (робоче) напруження  не перевищує допустимого []:

 

.

Допустимі напруження – це максимальні значення напружень, за яких забезпечується надійна робота конструкції:

 

,

 

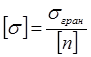де: σ_гран – граничні напруження (напруження, за яких відбувається порушення роботи або руйнування деталей конструкції), для конструкцій з пластичних матеріалів граничним напруженням є межа текучості σ_т, а для крихких матеріалів – це межа міцності σ_м;

       [n]  – допустимий (мінімально необхідний) коефіцієнт запасу міцності.

Для конструкцій з пластичних матеріалів допустимі напруження на розтяг і стиск однакові, тому для них σ – найбільше за абсолютною величиною напруження. Крихкі матеріали значно гірше працюють на розтяг, ніж на стиск:

 

[σ_ст] 3-5[σ_р],

 

де: [σ_ст] – допустиме напруження стиску;

       [σ_р] – допустиме напруження розтягу.

 

Умова міцності для крихкого матеріалу:

 

            ,

 

де σ_ст, σ_р – найбільші розрахункові напруження стиску і розтягу.

Залежно від мети розрахунку можна виконати три види розрахунків на міцність:

1) Перевірка міцності (перевірний розрахунок) – за заданої поздовжньої сили N і площі поперечного перерізу А визначають робоче (розрахункове) напруження порівнюють його з допустимим:

.

Допускається недовантаження до 5 %, перевантаження до 10 %.

 

2) Підбір поперечного перерізу (проектний розрахунок) – за відомих поздовжньої сили N і допустимого напруження [σ] визначають необхідні розміри перерізу:

 .

3) Визначення допустимого навантаження:

 

 

Приклад. Для заданого бруса побудувати епюри: а) поздовжньої сили N, б) нормальних напружень в поперечному перерізі σ, в) переміщення вільного кінця бруса λ. Схема навантаження зображена на рис.

 

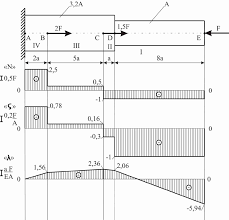
Для побудови епюр скористаємося методом перерізів. Розділимо брус на чотири зони (I-IV), межами яких є точки прикладення зовнішніх сил або точки зміни площі поперечного перерізу. Визначимо поздовжні зусилля на кожній ділянці:

 

Поздовжнє зусилля не залежить від координати перерізу, тому у всіх перерізах діє одне і теж внутрішнє зусилля (на кожній своє). По характерним точкам будуємо епюру поздовжніх сил «N». Аналізуючи епюру поздовжніх сил, визначаємо, що III і IV ділянки працюють на розтяг, а I та II ділянки працюють на стиск.

Для кожної ділянки визначаємо величину нормального напруження:

 

 По характерним точкам будуємо епюру нормальних напружень «σ ». Аналізуючи епюру нормальних напружень, визначаємо, що небезпечною ділянкою для бруса буде ділянка I, на якій нормальні напруження (за модулем) мають максимальне значення.

Для кожної ділянки визначаємо абсолютне подовження або укорочення та визначаємо загальне абсолютне подовження бруса, прийнявши = 0 , оскільки в точці закріплення деформації бруса не буде:

Отже, довжина бруса зменшиться на одиниць. По характерним точкам будуємо епюру укорочення бруса «».

Цікаві новини   Замовлення реферату

СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ

1. Писаренко Г.С. Опір матеріалів / Г.С. Писаренко, О.Л. Квітка, Е.С. Уманський. – К.: Вища школа, 1993. – 655 с.

2. Феодосьев В.И. Сопротивление материалов: Учебник для ВТУЗов / В.И. Феодосьев. – М.: Наука, 1986. – 512 с.

3. Мироненко П.С. Методичні вказівки для виконання практичних робіт з курсу «Прикладної механіки» / П.С. Мироненко, П.М. Бондар. – К.: КПІ, 1995.

4. Опір матеріалів: Навч. посіб. для студентів ВНЗ. Рекомендовано МОН / Шваб'юк В. І. — К., 2009. — 380 с.

5. Розтяг-стиск // / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. —173с.