Методичний посібник по підготовці до ДПА(ЗНО) учнів 9-х класів , та вступу до технікумів і ліцеїв, коледжів
В посібнику з математики коротко викладено теоретичний мінімум, який повинний знати кожен учень. В додатках до збірника даються тести та відповіді до них, а також варіанти екзаменаційних завдань попередніх років. Викладений матеріал цілком достатній для успішної здачі ДПА(ЗНО) з математики в школі і при вступі технікумів, ліцеїв та коледжів.
Маріупольська загальноосвітня школа-інтернат № 2
Донецької обласної ради

Методичний посібник по підготовці до ДПА(ЗНО)
учнів 9-х класів , та вступу до технікумів і ліцеїв, коледжів
Маріуполь 2018
___________________________________________________
Рецензент: Келюх І.О.
В посібнику з математики коротко викладено теоретичний мінімум, який повинний знати кожен учень. В додатках до збірника даються тести та відповіді до них, а також варіанти екзаменаційних завдань попередніх років. Викладений матеріал цілком достатній для успішної здачі ДПА(ЗНО) з математики в школі і при вступі технікумів, ліцеїв та коледжів.
Для учнів 9-х класів і вступників у технікуми та ліцеї, коледжі.
Автор: Скрипник Г.Г.
Тема 1. Натуральні числа і дії над ними
Натуральні числа
Натуральні числа — це числа, що використовуються для лічби: 1,2,3,.... n.... Множину натуральних чисел позначають символом N. N={1, 2, 3,...}
Будь-яке натуральне число п у десятковій системі числення можна подати у вигляді n = аk ∙ 10k + аk-1 ∙ 10k-1 + ... + а2 ∙102 + а1 ∙ 101 + а0, де а0, a1, a2, ..., ak-1 можуть набувати значення 0,1, 2, 3, 4, 5, 6, 7, 8, 9, а число аk — значення 1, 2, 3, 4, 5, 6, 7, 8, 9.
Позиційний запис числа має вигляд: Наприклад: 732 = 7 ∙ 102 + 3 ∙ 10 + 2;
13 859 = 1 ∙ 104 + 3 ∙ 103 + 8 ∙ 102 + 5 ∙ 10 + 9.
Порівняння натуральних чисел
Із двох натуральних чисел більшим (меншим) є те число, яке при лічбі з’являється пізніше (раніше). Наприклад: 17 < 20; 129 > 120.
Найменшим натуральним числом є число 1. Найбільшого натурального числа не існує.
Із двох натуральних чисел із різною кількістю цифр більшим є те, яке позначене більшою кількістю цифр. Якщо два натуральних числа мають однакову кількість цифр, то більшим є те число, в якому більше одиниць у найвищому розряді. Якщо кількість одиниць у цьому розряді однакова, то порівнюються розряди, що на один ступінь нижче і т. д. Наприклад: 10256 > 989; 10256 < 10356.
Округлення натуральних чисел
Щоб округлити натуральне число до певного розряду, треба:
1) замінити нулями всі цифри, що стоять після цього розряду;
2) якщо наступна за цим розрядом цифра була 5, 6, 7, 8 або 9, то цифру розряду, до якого виконується округлення, збільшити на одиницю; якщо наступна за цим розрядом цифра була 0, 1, 2, 3 або 4, то цифру розряду, до якого виконується округлення, залишити без змін.
Наприклад: числа 125 128, 59 393 округлені до десятків, до сотень відповідно дорівнюють 125 130, 59 390 і 125 100 і 59 400, тобто 125 128 ≈ 126 130, 59 393 ≈ 59 390, 125 128 ≈ 125 100, 59 393 ≈ 59 400.
Додавання натуральних чисел: а+ в =с (доданок + доданок = сума)
Наприклад: 5 + 3 = 5 + 1 + 1 + 1=8.
Додавання багатоцифрових натуральних чисел виконується порозрядно (додавання одноцифрових чисел кожного стовпчика, починаючи з правого стовпчика). Наприклад:
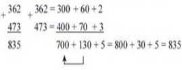
Віднімання натуральних чисел: а - в =с (зменшуване - від’ємник = різниця)
Відняти від числа а число b означає знайти таке число с, що а = b + с.
Наприклад: 10 - 3 = 10 - 1 - 1 - 1 = 7.
Віднімання багатоцифрових натуральних чисел виконується порозрядно (віднімання чисел кожного стовпчика, починаючи з правого стовпчика):
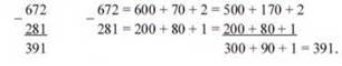
Множення натуральних чисел: а*в =с (множник* множник = добуток)
Наприклад: 2 ∙ 3 = 2 + 2 + 2 = 6.
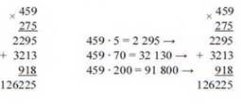 Множення багатоцифрових натуральних чисел виконується «у стовпчик».
Множення багатоцифрових натуральних чисел виконується «у стовпчик».
Наприклад:
Ділення натуральних чисел: ділене: дільник = частка
Розділити число а на число b означає знайти число с таке, що а = b ∙ с.
Натуральне число а розділити на натуральне число b означає підрахувати, скільки разів треба відняти число b від числа а, щоб одержати нуль.
Наприклад: 6 : 3 = 2, бо 6 - 3 - 3 = 0.
Натуральне число а ділиться на натуральне число b націло (а : b), якщо існує натуральне число с таке, що а = bс.
Наприклад: 6 ⋮ 2; 15 ⋮ 5. Якщо а ⋮ b, то b — дільник а; а— кратне b.
Властивості подільності:
0 ⋮ а, а ∈ N; а ⋮ 1, a ∈ N; а ⋮ a, a ∈ N.
Якщо а ⋮ b, a ∈ N, b ∈ N, то а ≥ b.
Якщо а ⋮ b, b ⋮ c, a ∈ N, b ∈ N, c ∈ N, то a ⋮ с.
Якщо а ⋮ с, b ⋮ с, а ∈ N, b ∈ N, c ∈ N, ТO (a + b) ⋮ c.
Якщо a ⋮ b і b ⋮ a, a ∈ N, b ∈ N, ТO a = b.
Якщо a ⋮ b, k ≠ 0, TO ak ⋮ bk.
Якщо a ⋮ c, b ⋮ c, a ∈ N, b ∈ N, c ∈ N, m ∈ N, n ∈ N, TO (am + bn) ⋮ c.
Якщо a ⋮ (bс), a ∈ N, b ∈ N, c ∈ N, тO a ⋮ b, a ⋮ c і (a ⋮ b) ⋮ c.
Якщо a ⋮ c i (a + b) ⋮ c, a ∈ N, b ∈ N, c ∈ N, ТO b ⋮ c
Ознаки подільності:
|
Число ділиться на |
2, якщо його остання цифра ділиться на 2 |
|
5, якщо його остання цифра ділиться на 5 |
|
|
4, якщо число, складене з двох останніх цифр, ділиться на 4 |
|
|
25, якщо число, складене з двох останніх цифр, ділиться на 25 |
|
|
3, якщо сума його цифр ділиться на 3 |
|
|
9, якщо сума його цифр ділиться на 9 |
|
|
10, якщо його остання цифра є 0 |
Ділення натуральних чисел і остачею
Якщо а —ділене, b — дільник і а = bс + r, де r < b, то говорять, що при діленні числа а на число b маємо неповну частку с та остачу r.
а : b = с (остача r). Наприклад: 10 : 4 = 2 (остача 2), 10 = 4 ∙ 2 + 2.
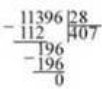 Ділення багатоцифрових чисел виконується «кутом». Наприклад:
Ділення багатоцифрових чисел виконується «кутом». Наприклад:
113 сотень : 28 = 4 сотні (остача 1 сотня).
19 десятків : 28 = 0 десятків (остача 19 десятків), 196 : 28 = 7.
Найбільший спільний дільник
Найбільшим спільним дільником чисел а і b називається найбільше число, на яке ділиться і число а, і число b. Позначення — НСД (а; b). Наприклад: НСД (5; 15) = 5. НСД (15; 9) = 3.
Найменше спільне кратне
Найменшим спільним кратним чисел а і b називається найменше число, яке ділиться і на число а, і на число b. Позначення — НСК (а; b). Наприклад: НСК (5; 15) = 15; НСК (15; 9) = 45.
Взаємно прості числа.
Числа а і b називаються взаємно простими, якщо НСД (а; b) = 1.
Наприклад: числа 3 і 5 взаємно прості, бо НСД (3; 5) = 1.
Прості та складені числа
Прості числа — натуральні числа, які мають рівно два різних дільники (одиницю і саме число). Наприклад: 2; 3; 5; 7; 11; 13; ... — прості числа.
Складені числа — натуральні числа, які мають більше двох дільників. Наприклад: 4; 6; 9; 10; ... — складені числа
Будь-яке складене число n можна розкласти на прості множники, тобто подати його у вигляді
n = ![]() ∙
∙ ![]() ∙ ... ∙, де Р1, Р2,.... Рk — прості числа а k, m1, m2, ..., mk — натуральні числа. Наприклад: 128 = 27; 24 = 23∙ 3; 108 = 22∙ 33.
∙ ... ∙, де Р1, Р2,.... Рk — прості числа а k, m1, m2, ..., mk — натуральні числа. Наприклад: 128 = 27; 24 = 23∙ 3; 108 = 22∙ 33.
Тема 2. Звичайні дроби і мішані числа та дії над ними.
Звичайні дроби і мішані числа
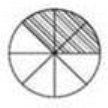 Звичайним дробом називається вираз
Звичайним дробом називається вираз ![]() , де а ∈ N. b ∈ N. Число а називається чисельником, а число b — знаменникам. Дробова риска означає знак ділення. Знаменник дробу показує, на скільки рівних частин ділитеся число (величина), чисельник — скільки таких частин узято.
, де а ∈ N. b ∈ N. Число а називається чисельником, а число b — знаменникам. Дробова риска означає знак ділення. Знаменник дробу показує, на скільки рівних частин ділитеся число (величина), чисельник — скільки таких частин узято.
Наприклад: дріб ![]() показує, що якусь величину розділили на 8 рівних частин і взяли три таких частини. 3 — чисельник. 8 — знаменник
показує, що якусь величину розділили на 8 рівних частин і взяли три таких частини. 3 — чисельник. 8 — знаменник ![]() = 3 : 8
= 3 : 8
Дріб називається правильним, якщо його чисельник менший за знаменник.
 Дріб називаєтеся неправильнім, якщо його чисельник дорівнює знаменнику або більший за нього.
Дріб називаєтеся неправильнім, якщо його чисельник дорівнює знаменнику або більший за нього.
Наприклад: дроби ![]() ;
; ![]() — правильні; дроби
— правильні; дроби ![]() ;
; ![]() — неправильні.
— неправильні.
Мішаним числом називається сума натурального числа і правильного дробу, записана без знака «+». Наприклад, число 1![]() мішане, число 1 — ціла частина мішаного числа, а
мішане, число 1 — ціла частина мішаного числа, а ![]() — дробова частина мішаного числа
— дробова частина мішаного числа
Виділення цілої частини із неправильного дробу.
Перетворення мішаного числа в неправильний дріб
Щоб із неправильного дробу виділити цілу частину, треба розділити з остачею чисельник на знаменник: неповна частка буде цілою частиною, остача — чисельником, а знаменник — той самий. Наприклад: ![]() ; 1
; 1 ![]() ;
; ![]() ; 5
; 5 ![]()
Щоб подати мішане число у вигляді неправильного дробу, треба помножити його цілу частину на знаменник дробової частини; до одержаного добутку додати чисельник дробової частини і записати суму чисельником, а знаменник залишити той самий. Наприклад: 2![]() =
= ![]() =
= ![]() ; 12
; 12 ![]() =
= ![]() =
= ![]() .
.
Основна властивість дробу
 Основна властивість дробу: якщо чисельник і знаменник дробу помножити або поділити на одне й те саме число, відмінне від нуля, то одержимо дріб, який дорівнює даному. Наприклад:
Основна властивість дробу: якщо чисельник і знаменник дробу помножити або поділити на одне й те саме число, відмінне від нуля, то одержимо дріб, який дорівнює даному. Наприклад: ![]() =
= ![]() =
= ![]() =
= ![]()
Скорочення дробу —ділення чисельника і знаменника дробу на спільний дільник чисельника і знаменника дробу, більший за одиницю.
Наприклад: ![]() =
= ![]() ;
; ![]() =
= ![]() .
.
Порівняння дробів і мішаних чисел
Із двох дробів із рівними знаменниками більший (менший) той дріб, у якого чисельник більший (менший). Наприклад: ![]() <
< ![]() ,
, ![]() >
> ![]() .
.
Щоб порівняти дроби з різними знаменниками, треба їх звести до спільного знаменника а потім порівняти. Наприклад: ![]() <
< ![]() , оскільки
, оскільки ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() >
> ![]() .
.
Із двох мішаних чисел з однаковими цілими частинами більше те число, дробова частина якого більша. Із двох мішаних чисел із різними цілими частинами більше те, ціла частина якого більша. Наприклад: 3![]() > 1
> 1![]() , 5
, 5![]() > 5
> 5![]() .
.
Додавання звичайних дробів і мішаних чисел
Додавання дробів із рівними знаменниками: ![]() +
+ ![]() =
= ![]() . Наприклад:
. Наприклад: ![]() +
+ ![]() =
= ![]() .
.
Додавання дробів із різними знаменниками: ![]() +
+ ![]() =
= ![]() , якщо НСД (b; d) = 1.
, якщо НСД (b; d) = 1.
Наприклад: ![]() +
+ ![]() =
= ![]() =
= ![]() .
.
![]() +
+ ![]() =
= ![]() , де m = НСК (b; d), k =
, де m = НСК (b; d), k = ![]() , l =
, l = ![]() . Наприклад:
. Наприклад: ![]() +
+ ![]() =
= ![]() =
= ![]() .
.
a + ![]() =
= ![]() . Наприклад: 5 =
. Наприклад: 5 = ![]() = 5
= 5![]() =
= ![]() =
= ![]() .
.
Віднімання звичайних дробів і мішаних чисел
Віднімання дробів із рівними знаменниками ![]() -
- ![]() =
= ![]() . Наприклад:
. Наприклад: ![]() -
- ![]() =
= ![]() .
.
Віднімання дробів із різними знаменниками
![]() -
- ![]() =
= ![]() , якщо НСД (b; d) = 1. Наприклад:
, якщо НСД (b; d) = 1. Наприклад: ![]() -
- ![]() =
= ![]() =
= ![]() .
.
![]() +
+ ![]() =
= ![]() , де m = НСК (b; d), k =
, де m = НСК (b; d), k = ![]() , l =
, l = ![]() . Наприклад:
. Наприклад: ![]() +
+ ![]() =
= ![]() =
= ![]()
a - ![]() =
= ![]() . Наприклад: 1 -
. Наприклад: 1 - ![]() =
= ![]() =
= ![]() ; 5 -
; 5 - ![]() =
= ![]() =
= ![]() .
.
Множення звичайних дробів
![]() ∙
∙ ![]() =
= ![]() . Наприклад:
. Наприклад: ![]() ∙
∙ ![]() =
= ![]()
![]() ∙
∙ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
a ∙ ![]() =
= ![]() . Наприклад: 5 ∙
. Наприклад: 5 ∙ ![]() =
= ![]() = 2;
= 2;
3 ∙ ![]() =
= ![]() = =1
= =1![]() .
.
Ділення дробів
![]() :
:![]() =
= ![]() ∙
∙![]() =
= ![]() . Наприклад:
. Наприклад: ![]() :
: ![]() =
= ![]() ∙
∙ ![]() =
= ![]()
a : ![]() = a ∙
= a ∙ ![]() =
= ![]() . Наприклад: 12 :
. Наприклад: 12 : ![]() = =12
= =12 ![]() =
= ![]() =
= ![]() = 18.
= 18.
![]() : c =
: c = ![]() ∙
∙![]() =
= ![]() Наприклад:
Наприклад: ![]() : 4 =
: 4 = ![]() =
= ![]() =
= ![]() .
.
Тема 3. Десяткові дроби та дії над ними
Десяткові дроби
Звичайні дроби (і мішані числа), знаменниками яких є числа 10,100,1000 і т. д., називаються десятковими. Десятковий дріб записують так: N, n1n2n3...nk, де N— ціле число, n1n2n3,... — десяті, соті, тисячні... частини. Наприклад: 0,25; 3,852; 101,01—десяткові дроби.
Запис десяткового дробу у вигляді звичайного дробу (мішаного числа) та запис звичайного дробу у вигляді десяткового
Щоб десятковий дріб записати у вигляді звичайного дробу (мішаного числа), треба число, що стоїть до коми, записати цілою частиною; число, що стоїть після коми, записати в чисельник, а в знаменнику поставити одиницю і стільки пулів, скільки стоїть цифр після коми. Наприклад: 5,62 = 5![]() = 5
= 5![]() .
.
Щоб записати звичайний дріб у вигляді десяткового, треба чисельник дробу поділити на знаменник. Наприклад: ![]() = 0,625;
= 0,625; ![]() = 0,666... = 0,(6).
= 0,666... = 0,(6).
Порівняння десяткових дробів
Щоб порівняти два десяткових дроби, треба спочатку порівняти цілі частини дробів; у разі їх рівності послідовно порівнюють десяті, якщо рівні десяті — порівнюють соті і т. д.
Наприклад: 10,23 > 9,85; 3,759 < 3,81.
Наближені значення даного числа
Якщо дане число заміняємо на інше число, близьке за значенням до даного, то одержуємо наближене значення даного числа. Наприклад: 122 ≈ 120 (читаємо: «122 наближено дорівнює 120») 1,9 ≈ 2 (читаємо: «одна ціла дев’ять десятих наближено дорівнює двом»). Якщо а < х < b, то а називають наближеним значенням числа х із недостачею, а b — наближеним значенням х із надлишкам.
Округлення десяткових дробів
При округленні десяткових дробів користуються одним із таких двох правил.
Правило 1
Щоб округлити десятковий дріб до певного розряду дробової частини (до певного десяткового знака), треба:
1) відкинути всі десяткові знаки, які стоять після цього розряду;
2) якщо перша з відкинутих цифр була 5, 6, 7, 8 або 9, то останню залишену цифру збільшити на одиницю;
3) якщо перша з відкинутих цифр була 0, 1, 2, 3 або 4, то останню залишену цифру записати без змін.
Приклад 1. Округлити дріб 3,212 до сотих і дріб 18,091 до десятих. Розв’язання. 3,212 ≈ 3,21; 18,091 ≈ 18,1.
Правило 2
Щоб округлити десятковий дріб до певного розряду цілої частини вищого розряду одиниць, треба: відкинути всі цифри дробової частини (всі десяткові знаки); цілу частину округлюємо за правилом округлення натуральних чисел.
Приклад 2. Округлити дроби 12 931,3102 і 118,35 до десятків.
Розв’язання. 12931,3102 ≈ 12 930; 118,35 ≈ 120.
 Додавання десяткових дробів
Додавання десяткових дробів
Додавання десяткових дробів виконується порозрядно. Наприклад:
 Віднімання десяткових дробів
Віднімання десяткових дробів
Віднімання десяткових дробів виконується порозрядно. Наприклад:
 Множення десяткових дробів
Множення десяткових дробів
Множення десяткових дробів виконується як множення натуральних чисел, у добутку справа відокремлюють комою стільки десяткових знаків, скільки їх мають обидва множники. Наприклад:
Ділення десяткового дробу
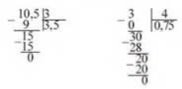 Ділення десяткового дробу на натуральне число виконується так само, як ділення натуральних чисел, тільки, закінчивши ділення цілої частини числа, треба в частці поставити кому. Наприклад:
Ділення десяткового дробу на натуральне число виконується так само, як ділення натуральних чисел, тільки, закінчивши ділення цілої частини числа, треба в частці поставити кому. Наприклад:
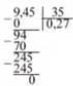
![]() Щоб поділити на десятковий дріб, треба в діленому і дільнику перенести кому вправо на стільки знаків, скільки їх є в дільнику, а потім виконати ділення на натуральне число:
Щоб поділити на десятковий дріб, треба в діленому і дільнику перенести кому вправо на стільки знаків, скільки їх є в дільнику, а потім виконати ділення на натуральне число:
Наприклад:
Тема 4. Раціональні числа та дії над ними
Цілі числа
Цілими числами називаються натуральні числа, їм протилежні числа і число 0. Множину цілих чисел позначають символом Z. Z= {..., -3, -2, -1, 0, 1, 2, 3, ...}
Подання цілого числа у вигляді дробу
Будь-яке ціле число а можна подати у вигляді дробу: a = ![]() , n ∈ N, a ∈ Z.
, n ∈ N, a ∈ Z.
Наприклад: 10 = ![]() =
= ![]() =
= ![]() = …
= …
Порівняння додатних і від’ємних чисел
Будь-яке від’ємне число менше нуля і будь-якого додатного числа. Нулі ≥ менше будь-якого додатного числа. Наприклад: -5 < 0; -5 < 1; 0 < 10.
Додавання від’ємних чисел та чисел із різними знаками
Додавання від’ємних чисел: -а + (-b) = -а - b = -(а + b), де а і b — додатні числа.
Наприклад: -5 - 3 = -8.
Додавання чисел із різними знаками:
Наприклад: -10 + 2 = -(10 - 2) = -8.
Наприклад: -3 + 10 = 10 - 3 = 7.
Віднімання додатних і від’ємних чисел
Відняти від числа а число b означає додати до числа а число, протилежне b:
а - b = а + (-b). Наприклад: 5 - 6 = 5 + (-6) = -1; -3 - (-5) = -3 + 5 = 2.
Множення додатних і від’ємних чисел
-а - b = a ∙ (-b) = - (ab), де а, b — додатні числа. Наприклад: -3 ∙ 5 = -15; 8 ∙ (-2) = -16.
-а ∙ (-b) = ab, де а, b — додатні числа. Наприклад: -3 ∙ (-5) = 15.
Ділення додатних і від’ємних чисел
а : (-6) = -а : b = -(а : b), де а і b — додатні числа. Наприклад: 6 : (-2) = -3; -12 : 3 = -4.
-a: (-b) = а : b, де а і b — додатні числа. Наприклад: -15 : (-5) = 3.
Раціональні числа
Раціональні числа — числа, які можна подати у вигляді ![]() , де m ∈ Z, n ∈ N. Множину раціональних чисел позначають символом Q.
, де m ∈ Z, n ∈ N. Множину раціональних чисел позначають символом Q.
Наприклад: -1; ![]() ; -2
; -2![]() ; 0 — раціональні числа.
; 0 — раціональні числа.
Будь-яке раціональне число — нескінченний періодичний десятковий дріб.
Нескінченний десятковий періодичний дріб
Нескінченний десятковий періодичний дріб — десятковий дріб, у якому нескінченно повторюється певна група цифр. Мінімальна група цифр, яка повторюється, називається періодом. Період записується в круглих дужках.
Наприклад: ![]() = 0,333... = 0,(3); 3,060606 = 3,(06);
= 0,333... = 0,(3); 3,060606 = 3,(06); ![]() = 0,3111... = 0,3(1).
= 0,3111... = 0,3(1).
Якщо період починається відразу після коми, то дріб називається чисто періодичним. Якщо ж період починається не відразу після коми, то дріб називається змішаним періодичним.
Перетворення нескінченного десяткового періодичного дробу у звичайний
Чисто періодичний десятковий дріб дорівнює звичайному дробу, чисельник якого є період, а знаменник — цифра 9, що записана стільки разів, скільки цифр у періоді.
Наприклад: 0,(3) = ![]() =
= ![]() ; 0,(81) =
; 0,(81) = ![]() =
= ![]() .
.
Для того щоб перетворити змішаний нескінченний періодичний дріб на звичайний, треба від числа, що стоїть до другого періоду, відняти число, що стоїть до першого періоду. Потім записати цю різницю чисельником, а в знаменнику записати цифру 9 стільки разів, скільки цифр у періоді, а після дев’яток дописати стільки нулів, скільки цифр стоїть між комою і першим періодом. Наприклад: 0,11(7) = ![]() =
=![]() =
= ![]() .
.
Властивості арифметичних дій
Властивості додавання: а + b = b + а (переставна);
(а + b) + с = а + (b + с) (сполучна); а + 0 = а; а + (-а) = 0.
Властивості віднімання: а - (b + с) = а - b - с;
(а + b) - с = (а - с) + b; а - 0 = а.
Властивості множення: а ∙ b = b ∙ а (переставна)
(а ∙ b) ∙ с = а ∙ (b ∙ с) (сполучна)
(q + b) ∙ c = ac + b ∙ c (розподільна властивість множення відносно додавання)
(a - b) c = a ∙ c - b ∙ c (розподільна властивість множення відносно віднімання)
а ∙ 1 = а; а ∙ 0 = 0 а ∙ ![]() = 1, якщо а ≠ 0.
= 1, якщо а ≠ 0.
Властивості ділення:
а : 1 = а; а : а = 1, а ≠ 0; 0 : а = 0, а ≠ 0. Hа нуль ділити не можна!
Пропорції ![]() =
= ![]() або а : b = с : d, де a, d — крайні члени, b, с — середні члени.
або а : b = с : d, де a, d — крайні члени, b, с — середні члени.
Пропорція ![]() =
= ![]() рівносильна рівностям: ad = bc
рівносильна рівностям: ad = bc ![]() =
= ![]() ;
; ![]() =
= ![]() ;
; ![]() =
= ![]() .
.
Похідні пропорції Якщо ![]() =
= ![]() і bd ≠ 0, то:
і bd ≠ 0, то: ![]() =
= ![]() ;
; ![]() =
= ![]() ;
; ![]() =
= ![]() ;
; ![]() =
= ![]() ;
; ![]() =
= ![]() .
.
Тема 5. Відсотки. Задачі на відсотки.
Відсотки
Соту частину будь-якої величини або числа називають відсотком (процентам). Слово «відсоток» замінюють знаком %, тобто 1% = ![]() = 0,01.
= 0,01.
Наприклад: 1 копійка — один відсоток від гривні, 1 см — один відсоток від метра, тобто
1 коп. = 1 % грн. 1 см = 1 % м.
Щоб перетворити десятковий дріб на відсотки, треба його помножити на 100.
Наприклад: 0,35 = 35 %; 0,3 = 30 %; 1,5 = 150 %.
Щоб перетворити відсотки на десятковий дріб, треба число відсотків розділити на 100. Наприклад: 30 % = 0,3; 53 % = 0,53; 1,58 % = 0,0158.
Основні задачі на відсотки
Для того щоб знайти р відсотків від даного числа а, треба:
1) перевести р відсотків у десятковий дріб;
2) помножити число а на одержаний десятковий дріб.
Приклад 1. Знайти 20 % від числа 120.
Розв'язання. 20 % = 0,2,120 ∙ 0,2 = 24. Відповідь: 24.
Для того щоб знайти все число за відомою частиною b і числом відповідних відсотків р. треба:
1) перевести р відсотків у десятковий дріб;
2) розділити b на одержаний десятковий дріб.
Приклад 2. Знайти число, 12 % якого складає 60. Розв’язання. 60 : 0,12 = 6000 : 12 = 500. Відповідь: 500.
Щоб знайти відсоток числа b від числа а, треба дріб ![]() помножити на 100 %.
помножити на 100 %.
Приклад 3. Скільки відсотків складає число 0,3 від 20?
Розв’язання.
![]() ∙ 100% =
∙ 100% = ![]() = 0,3 ∙ 5% = 1,5%. Відповідь: 1,5 %.
= 0,3 ∙ 5% = 1,5%. Відповідь: 1,5 %.
Збільшення (зменшення) числа на декілька відсотків. Формула складних відсотків
|
Збільшення на р % |
Зменшення на р % |
Формула складних відсотків |
|
Якщо число а збільшити на р %, то одержимо число
а ∙ (1 + Якщо число 200 збільшити на 30 %, то одержимо число 200(1 + 0,3) = =200 ∙ 1,3 = 260. |
Якщо число а зменшити на р %, то одержимо число
а (1 - Якщо число 120 зменшити на 30 %, то одержимо число 120 ∙ (1 - 0,3) = = 120 ∙ 0,7 = 84. |
Якщо А — початковий вклад (капітал), р — річний відсоток, то в кінці n-го року вклад (капітал) становитиме
A ∙ (1 + |
Розв'язування більш складних задач на відсотки
Задача 1. На заводі 40 % усіх верстатів переведено на підвищені швидкості, унаслідок чого продуктивність праці зросла на 30 %. На скільки відсотків збільшилося виробництво заводської продукції?
Розв'язання: Нехай х — загальний обсяг продукції, що випускав завод раніше.
Знайдемо, на скільки збільшився загальний обсяг продукції: х ∙ 0,4 ∙ 0,3 = 0,12х.
Знайдемо, на скільки відсотків збільшилося виробництво заводської продукції: ![]() ∙ 100% = 12%.
∙ 100% = 12%.
Відповідь: на 12 %.
Задача 2. На скільки відсотків збільшиться продуктивність праці робітників, якщо час на виконання певної операції скоротати на 20 %?
Розв'язання: Нехай х — час виконання операції, тоді ![]() — продуктивність праці; 0,8 х — час на виконання операції після його скорочення, тоді
— продуктивність праці; 0,8 х — час на виконання операції після його скорочення, тоді ![]() =
= ![]() — нова продуктивність праці,
— нова продуктивність праці, ![]() -
- ![]() =
= ![]() — величина, на яку збільшиться продуктивність праці. Отже, продуктивність праці робітників збільшиться на 100%:
— величина, на яку збільшиться продуктивність праці. Отже, продуктивність праці робітників збільшиться на 100%: ![]() ∙
∙ ![]() =
= ![]() = 25%. Відповідь: на 25 %.
= 25%. Відповідь: на 25 %.
Задача 3. На скільки відсотків збільшиться реальна зарплатня, якщо ціни на всі продовольчі та промислові товари зменшити на 20 %?
Розв'язання: Нехай х — початкова ціна товарів, тоді ![]() — реальна заробітна плата 0,8х — нова ціна товарів, тоді
— реальна заробітна плата 0,8х — нова ціна товарів, тоді ![]() =
= ![]() — реальна заробітна плата. Отже, реальна платня збільшилася на
— реальна заробітна плата. Отже, реальна платня збільшилася на
100%: ![]() ∙ (
∙ (![]() ) =
) = ![]() = 25%. Відповідь: на 25 %.
= 25%. Відповідь: на 25 %.
Тема 6. Степінь із натуральним і цілим показниками
Степінь iз натуральним показником та його властивості
![]() Степенем числа а з натуральним показником я, більшим за одиницю, називають добуток n множників. кожний із яких дорівнює а.
Степенем числа а з натуральним показником я, більшим за одиницю, називають добуток n множників. кожний із яких дорівнює а.
Першим степенем числа називають саме число: а1 = а. Наприклад: 51 = 5;(-2)3 = -2 ∙ (-2) ∙ (-2) =-8. 34 = 3 ∙ 3 ∙ 3 ∙ 3 = 81; 0n = 0, n ∈ N
1n = 1, n ∈ N. У записі аn = b число а називається основою степеня, n — показником степеня, an — степенем, b — значенням степеня.
Властивості степенів
1. При множенні степенів із рівними основами основа залишається такою самою, а показники степенів додаються: аm ∙ аn = аm+n.
2. При діленні степенів із рівними основами основа залишається такою самою, а показники віднімаються: am : an = am-n, або ![]() = am-n.
= am-n.
3. При піднесенні степеня до степеня основа залишається такою самою, а показники перемножуються: (аm)n = аmn.
4. При піднесенні до степеня добутку до цього степеня підноситься кожний множник: (аb)n =аnbn.
5. При піднесенні до степеня дробу до цього степеня підносяться чисельник і знаменник: (![]() )n =
)n = ![]() .
.
Піднесення до степеня вважається арифметичного дією третього ступеня. Якщо вираз містить різні арифметичні дії, то спочатку виконується піднесення до степеня як дія вищого (третього) ступеня, потім множення і ділення (дії другого ступеня) і, нарешті, додавання і віднімання (дії першого ступеня).
Наприклад: 5 ∙ 23 - 62 : 12 = 5 ∙ 8 - 36 : 12 = 40 - 3 = 37.
Степінь із цілим показником та його властивості
Нульовий степінь числа, відмінного від нуля, дорівнює одиниці. Нульовий степінь нуля не визначений. а0 = 1, а ≠ 0, 00 — не визначений.
Якщо а ≠ 0 i n ∈ N, то a-n = ![]() . Вираз 0-n, де n ∈ N — не визначений.
. Вираз 0-n, де n ∈ N — не визначений.
Наприклад: 2-3 = ![]() =
= ![]() , (-3)-3 =
, (-3)-3 = ![]() =
= ![]() .
.
Для степенів із цілими показниками характерні ті ж властивості, що й для степенів із натуральними показниками:
1. аn ∙ am = am+n;
2. am : an = am-n
3. (am)n = аmn;
4. (аb)n = аnbn;
5. (![]() )n =
)n = ![]() .
.
6. При піднесенні дробу до степеня з від’ємним показником можна піднести обернений дріб до степеня з протилежним показником: (![]() )-n = (
)-n = (![]() )n.
)n.
Стандартний вигляд числа
Стандартним виглядом числа а називають такий його запис: а ∙ 10n, де 1 ≤ а < 10 і n ∈ Z. Число n називають порядком числа
Наприклад: число а = 125 000 записують у стандартному вигляді так: а = 1,25 ∙ 105, а число а = 0,000508 так: а = 5,08 ∙ 10-4.
Тема 7. Одночлени та дії над ними
Буквені вирази. Числові значення буквених виразів
Буквеним виразом називають запис, у якому числа і букви з’єднано знаками дій.
Наприклад: х + 2, х + у, 3x - 2у, — ![]() буквені вирази.
буквені вирази.
Буквені вирази називають також виразами зі змінними, а букви — змінними. Якщо в буквений вираз замість букв підставити числа, то одержимо числовий вираз, значения якого називається числовим значенням буквеного виразу при даних значеннях букв.
Наприклад: якщо а = 3,5; b = 1,5, то значенням виразу ![]() є значення виразу
є значення виразу ![]() =
= ![]() = 1,05.
= 1,05.
Якщо вираз не містить ніяких інших дій. крім додавання, віднімання, множення, піднесення до натурального степеня і ділення, його називають раціональним.
Наприклад: 2ху + х, ![]() ,
, ![]() — раціональні вирази.
— раціональні вирази.
Раціональний вираз, який не містить ділення на вираз зі змінною, називають цілим. Наприклад: x + у, 2ху — цілі вирази.
Одночлени
Одночленам називається добуток чисел, змінних так натуральних степенів, а також самі числа, змінні та їх натуральні степені.
Наприклад: 5а, 6а2b, 3, х, xyz — одночлени.
Одночлен стандартного вигляду — одночлен, який містить тільки один числовий множник, що стоїть на першому місці, і степені з різними буквеними основами.
Наприклад: 3ab, 12х2y2z, -а,-х2у — одночлени стандартного вигляду.
Коефіцієнтам одночлена називають числовий множник одночлена стандартного вигляду.
Наприклад: коефіцієнтами одночленів 5x2, -3ab, -a2y, xyz є відповідно числа 5, -3, -1, 1. Коефіцієнти 1 та -1 в одночленах не записують.
Щоб записати одночлен у стандартному вигляді, треба перемножили всі його числові множники й одержане число поставити на перше місце, а потім добутки однакових буквених множників записати у вигляді степенів.
Наприклад: 2ab ![]() (-3а2b) ∙ (-3a3b) = 18a6b3.
(-3а2b) ∙ (-3a3b) = 18a6b3.
Степенем одночлена називають суму показників степенів усіх буквених множників, що входять до одночлена
Наприклад: степінь одночлена 5х3уz6? дорівнює 3 + 1 + 6 =10.
Якщо одночленом є число, відмінне від нуля, то вважають, що його степінь дорівнює нулю.
Дії над одночленами
Щоб помножити одночлен на одночлен, треба перемножити їх коефіцієнти і перемножити степені з однаковими основами.
Наприклад: 12а2у ∙ (-2аb3у3) = -24а3b3у4.
Щоб піднести одночлен до степеня, треба піднести його коефіцієнт до цього степеня і помножити показник степеня кожної букви на показник степеня, до якого підноситься одночлен.
Наприклад: (-3a2bx5)2= 9a4b2x10.
Щоб поділити одночлен на одночлен, треба поділити коефіцієнт діленого на коефіцієнт дільника, до знайденої частки приписати множниками кожну змінну діленого з показником, що дорівнює різниці показників цієї змінної в діленому і дільнику.
Наприклад: 12x7y3z12 : (4х3уz7) = 3х7-3у3-1z12-7 = 3x4y2z5.
Тема 7. Одночлени та дії над ними
Буквені вирази. Числові значення буквених виразів
Буквеним виразом називають запис, у якому числа і букви з’єднано знаками дій.
Наприклад: х + 2, х + у, 3x - 2у, — ![]() буквені вирази.
буквені вирази.
Буквені вирази називають також виразами зі змінними, а букви — змінними. Якщо в буквений вираз замість букв підставити числа, то одержимо числовий вираз, значения якого називається числовим значенням буквеного виразу при даних значеннях букв. Наприклад: якщо а = 3,5; b = 1,5, то значенням виразу ![]() є значення виразу
є значення виразу ![]() =
= ![]() = 1,05.
= 1,05.
Якщо вираз не містить ніяких інших дій. крім додавання, віднімання, множення, піднесення до натурального степеня і ділення, його називають раціональним.
Наприклад: 2ху + х, ![]() ,
, ![]() — раціональні вирази.
— раціональні вирази.
Раціональний вираз, який не містить ділення на вираз зі змінною, називають цілим. Наприклад: x + у, 2ху — цілі вирази.
Одночлени
Одночленам називається добуток чисел, змінних так натуральних степенів, а також самі числа, змінні та їх натуральні степені.
Наприклад: 5а, 6а2b, 3, х, xyz — одночлени.
Одночлен стандартного вигляду — одночлен, який містить тільки один числовий множник, що стоїть на першому місці, і степені з різними буквеними основами.
Наприклад: 3ab, 12х2y2z, -а,-х2у — одночлени стандартного вигляду.
Коефіцієнтам одночлена називають числовий множник одночлена стандартного вигляду.
Наприклад: коефіцієнтами одночленів 5x2, -3ab, -a2y, xyz є відповідно числа 5, -3, -1, 1. Коефіцієнти 1 та -1 в одночленах не записують.
Щоб записати одночлен у стандартному вигляді, треба перемножили всі його числові множники й одержане число поставити на перше місце, а потім добутки однакових буквених множників записати у вигляді степенів.
Наприклад: 2ab ![]() (-3а2b) ∙ (-3a3b) = 18a6b3.
(-3а2b) ∙ (-3a3b) = 18a6b3.
Степенем одночлена називають суму показників степенів усіх буквених множників, що входять до одночлена
Наприклад: степінь одночлена 5х3уz6? дорівнює 3 + 1 + 6 =10.
Якщо одночленом є число, відмінне від нуля, то вважають, що його степінь дорівнює нулю.
Дії над одночленами
Щоб помножити одночлен на одночлен, треба перемножити їх коефіцієнти і перемножити степені з однаковими основами. Наприклад: 12а2у ∙ (-2аb3у3) = -24а3b3у4.
Щоб піднести одночлен до степеня, треба піднести його коефіцієнт до цього степеня і помножити показник степеня кожної букви на показник степеня, до якого підноситься одночлен.
Наприклад: (-3a2bx5)2= 9a4b2x10.
Щоб поділити одночлен на одночлен, треба поділити коефіцієнт діленого на коефіцієнт дільника, до знайденої частки приписати множниками кожну змінну діленого з показником, що дорівнює різниці показників цієї змінної в діленому і дільнику. Наприклад: 12x7y3z12 : (4х3уz7) = 3х7-3у3-1z12-7 = 3x4y2z5.
Тема 8. Многочлени та дії над ними
Многочлени
Многочленам називається алгебраїчна сума кількох одночленів.
Наприклад: 3ху + ab + 2; 172b - 2ху + а—многочлени.
Одночлени, з яких складається многочлен, називають його членами. Одночлен — окремий вид многочлена. Многочлен, який містить два або три доданки, називають відповідно двочленом або тричленом.
Наприклад: а2 - b2, х + у — двочлени; а + ab + b, х2 + ху - у2 — тричлени.
Подібні члени многочлена — це однакові одночлени, або одночлени, запис яких у стандартному вигляді відрізняється лише коефіцієнтами.
Наприклад: у многочлені 15a2b + 3ab2 - 7a2b + 5аb2 перший і третій, другий і четвертий члени подібні.
Зведення подібних членів — це спрощення многочлена, при якому алгебраїчна сума подібних членів замінюється одним членом. Щоб звести подібні члени, треба додати їх коефіцієнти і результат помножити на їх спільну буквену частину.
Наприклад: 15а2b + 3аb2 - 7а2b + 5ab2 = 8a2b + 8аb2.
Стандартний вигляд многочлена — це запис многочлена, усі члени якого мають стандартний вигляд і серед них немає подібних.
Наприклад: а2 - ab + b2, ab + bс + ас — многочлени стандартного вигляду, а 3а2 + 2b2 - 3аb + а2 — многочлен нестандартного вигляду.
Степенем многочлена стандартного вигляду називають найбільший зі степенів одночленів, із яких складається многочлен. Степенем довільного многочлена називають степінь тотожно рівного йому многочлена стандартного вигляду.
Наприклад: степінь многочлена 5a7b + 5аb5 - 2а5b5 дорівнює степеню одночлена -2а5b5, тобто 5 + 5= 10.
Дії над многочленами
При додаванні многочленів користуються правилом розкриття дужок: якщо перед дужками стоїть знак «+», то дужки можна опустити, зберігши знаки кожного одночлена.
Наприклад: (3х2 - 2х + 5) +(6х2 + 5х - 3) = 3х2 - 2х + 5 + 6х2 + 5х - 3 = 9х2 + 3х + 2.
При відніманні многочленів користуються правилом розкриття дужок: якщо перед дужками стоїть знак «-», то дужки можна опустити, змінивши знак кожного одночлена, що містився в дужках, на протилежний.
Наприклад: (3х2 - 2х + 5) - (6х2 + 5х - 3) = 3х2 - 2х + 5 - 6х2 - 5х + 3= -3х2 - 7х +8.
Щоб записати алгебраїчну суму кількох многочленів як многочлен стандартного вигляду, треба розкрити дужки і звести подібні члени.
Наприклад: (2x2 - 3х + 2) - (3х2 - 2х -1) - (-х2 + 2х +1) + (-2х2 + х - 1) = 2х2 - 3х + 2 - 3х2 + 2х + 1 + х2 - 2х - 1 - 2х2 + х - 1 = -2х2 - 2х +1.
Щоб помножити одночлен на многочлен, треба кожний член многочлена помножити на цей одночлен й одержані одночлени додати.
Наприклад: 3а(а2 - 2а + аb) = 3а3 - 6а2 + 3а2b.
Щоб помножити многочлен на многочлен, треба кожний член одного многочлена помножити на кожний член другого многочлена й одержані одночлени додати.
Наприклад: (3х - 2)(2х - 3) = 3х ∙ 2х - 3х ∙ 3 - 2 ∙ 2х + 2 ∙ 3 = 6х2 - 9х - 4х + 6 = 6х2 - 13х + 6.
Щоб розділити многочлен на одночлен, треба кожний член многочлена розділити на цей одночлен й одержані результати додати.
Наприклад: (5х7 - 2х5 + 3х2 + 6х) : 2х = 5х7 : 2х - 2х5 : 2х + 3х2 : 2х + 6х : 2х = 2,5х6 - --х4 + 1,5х + 3.
Розкладанням многочлена на множники називають запис многочлена у вигляді добутку многочленів.
Наприклад: 2ах + 6ау = 2а(х + 3y).
При розкладанні многочлена на множники використовують такі способи.
1. Винесення спільного множника за дужки. Наприклад: 5х2 +10х = 5х(х + 2).
2. Спосіб групування.
Наприклад: 3х - 3у - х2 + ху = (3х - 3у) - (х2 - ху) = 3(х - у) - х(х - у) = (х - у)(3 - х).
3. Використання формул скороченого множення.
Формули скороченого множення
Квадрат суми двох виразів дорівнює квадрату першого виразу плюс подвоєний добуток першого і другого виразів плюс квадрат другого виразу
(а + b)2 = а2 + 2 ab + b2. Наприклад: (3а + 2b)2 = 9а2 +12аb + 4b2.
Квадрат різниці двох виразів дорівнює квадрату першого виразу мінус подвоєний добуток першого і другого виразів плюс квадрат другого виразу
(а - b)2 = а2 - 2ab + b2. Наприклад: (3а - 2)2 = 9а2 - 12а + 4.
Добуток різниці двох виразів і їх суми дорівнює різниці квадратів цих виразів
(а - b)(а + b)= а2 - b2. Наприклад: (5а - 3b)(5а + 3b) = 25а2 - 9b2.
Добуток суми двох виразів на неповний квадрат їх різниці дорівнює сумі кубів цих виразів
(a + b)(a2 - ab + b2) - а3 + b3. Наприклад: (3 + x)(9 - 3x + х2) = 27 + х3.
Добуток різниці двох виразів на неповний квадрат їх суми дорівнює різниці кубів цих виразів
(a - b)(a2 +ab + b2) = а3 - b3. Hаприклад : (2х - 3y)(4х2 + 6ху + 9у2) = 8x3 - 27у3.
Куб суми (різниці) двох виразів дорівнює кубу першого виразу плюс (мінус) потроєний добуток квадрата першого виразу на другий вираз плюс потроєний добуток першого виразу на квадрат другого виразу плюс (мінус) куб другого виразу (a ± b)3 = а3 ± 3а2b + 3ab2 ± b3.
Наприклад: (2х - 3у)3 = 8х3 - 36х2у + 54хy2 -27y3; (2 + 5х)3 = 8 + 60х+ 150х2 + 125х3.
Тема 9. Алгебраїчні дроби та дії над ними
Алгебраїчний дріб
Алгебраїчним називається дріб, чисельник і знаменник якого є алгебраїчними виразами.
Наприклад: ![]() ;
; ![]() ;
; ![]() — алгебраїчні дроби.
— алгебраїчні дроби.
Передбачається, що використані в записі алгебраїчного дробу букви можуть набувати тільки таких значень, при яких знаменник цього дробу не дорівнює нулю. Наприклад: дріб ![]() має зміст при всіх значеннях змінної а, крім 0 і 9.
має зміст при всіх значеннях змінної а, крім 0 і 9.
Основна властивість дробу
При множенні чисельника і знаменника дробу на один і той самий алгебраїчний вираз одержуємо дріб, що дорівнює даному дробу. Наприклад: ![]() =
= ![]() =
= ![]() .
.
Скорочення алгебраїчних дробів
Використовуючи основну властивість дробу, можна скорочувати алгебраїчні дроби на спільний множник чисельника і знаменника.
Наприклад: ![]() =
= ![]() =
= ![]() .
.
Якщо змінити знак чисельника (або знак знаменника) дробу і знак перед дробом, то одержимо вираз, що тотожно дорівнює даному: -![]() =
= ![]() ; -
; -![]() =
= ![]() .
.
Дії з дробами
Щоб додати (відняти) дроби з однаковими знаменниками, треба додати (відняти) їх чисельники, а знаменник залишити той самий.
Наприклад: ![]() +
+![]() =
= ![]() =
= ![]() ;
; ![]() -
- ![]() =
= ![]() =
= ![]() =
= ![]() .
.
Щоб додати (відняти) дроби з різними знаменниками, треба:
1) розкласти на множники чисельник і знаменник кожного дробу;
2) скоротити множники в чисельнику і знаменнику кожного дробу;
3) знайти і записати спільний знаменник дробів;
4) знайти і записати додаткові множники для кожного дробу;
5) записати суму (різницю) добутків чисельників і додаткових множників, ураховуючи знаки, в чисельник дробу;
6) спростити (якщо можливо) одержаний дріб.
Наприклад: ![]() +
+ ![]() -
- ![]() =
= ![]() +
+ ![]() -
- ![]() =
=![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
Щоб помножити дріб на дріб, треба перемножити їх чисельники і перемножити їх знаменники перший добуток записати чисельником, а другий — знаменником дробу.
Якщо b ≠ 0, d ≠ 0, то ![]() ∙
∙ ![]() =
= ![]() .
.
Наприклад: ![]() ∙
∙ ![]() =
= ![]() =
= ![]() .
.
Щоб розділити один дріб на інший, треба перший дріб помножити на дріб, обернений до другого.
Якщо b ≠ 0, с ≠ 0 і d ≠ 0, то ![]() :
:![]() =
= ![]() ∙
∙![]() . Наприклад:
. Наприклад: ![]() :
: ![]() =
= ![]() ∙
∙ ![]() =
= ![]() .
.
Тотожне перетворення раціональних алгебраїчних виразів
Виконати тотожні перетворення раціонального виразу (виразів) загального вигляду, що містить цілі і дробові вирази, означає звести вираз (вирази) до дробу, чисельник і знаменник якого є многочленами стандартного вигляду. При цьому послідовність виконання перетворень така сама, як і послідовність виконання дій у числових виразах.
Наприклад: I спосіб ![]() =
= 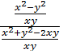 =
= ![]() ∙
∙ ![]() =
= ![]() =
= ![]() .
.
II спосіб ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
Тема 10. Арифметичний квадратний корінь. Цілі числа
Квадратний корінь.
Квадратним коренем із числа а називається число, квадрат якого дорівнює а. Наприклад: квадратний корінь із числа 4 дорівнює 2 або -2, бо 22 = 4, (-2)2 = 4.
Арифметичний квадратний корінь
Арифметичнім квадратним коренем із числа а називається невід’ємне число, квадрат якого дорівнює а. Арифметичний квадратний корінь із числа а позначають так: ![]() . Знак
. Знак ![]() називають знакам арифметичного квадратного кореня, вираз, який стоїть під знаком кореня. — підкореневим виразом. Запис
називають знакам арифметичного квадратного кореня, вираз, який стоїть під знаком кореня. — підкореневим виразом. Запис ![]() читають так: «квадратний корінь із а» (слово «арифметичний» при читанні опускають).
читають так: «квадратний корінь із а» (слово «арифметичний» при читанні опускають).
Отже, ![]() = b, b
= b, b ![]() 0 означає b2 = а.
0 означає b2 = а.
Якщо а < 0, то вираз ![]() не має змісту.
не має змісту.
Наприклад: ![]() = 4, бо 42 = 16;
= 4, бо 42 = 16; ![]() = 15, бо 152 = 225.
= 15, бо 152 = 225.
З означення арифметичного квадратного кореня випливає, що при невід’ємних значеннях а справедлива рівність (![]() )2 = а.
)2 = а.
Якщо а ![]() 0, то
0, то ![]() = а. Якщо а < 0, то
= а. Якщо а < 0, то ![]() = -а. Отже.
= -а. Отже.
![]() = |a| =
= |a| = ![]()
Властивості арифметичних квадратних коренів
1. Корінь із добутку невід’ємних множників дорівнює добутку коренів із цих множників:
![]() =
= ![]() ∙
∙ ![]() , де а
, де а ![]() 0, b
0, b ![]() 0. Якщо а
0. Якщо а ![]() 0, b > 0, то
0, b > 0, то ![]() ∙
∙ ![]() =
= ![]() .
.
Наприклад: ![]() =
= ![]() ∙
∙ ![]() = 8 ∙ 0,2 = 1,6;
= 8 ∙ 0,2 = 1,6; ![]() ∙
∙ ![]() =
= ![]() =
= ![]() = 4.
= 4.
2. Корінь із дробу, чисельник якого невід’ємний, а знаменник додатний, дорівнює кореню із чисельника, діленому на корінь зі знаменника:
![]() =
= ![]() , де а
, де а ![]() 0, b > 0. Якщо а
0, b > 0. Якщо а ![]() 0, b > 0, то
0, b > 0, то ![]() =
= ![]() .
.
Наприклад: ![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() = 4.
= 4.
3. Внесения множника під знак квадратного кореня:
а) b![]() =
= ![]() , при b
, при b ![]() 0;
0;
б) b![]() =
=![]() , при b < 0;
, при b < 0;
4. Винесення множника з-під знака кореня:
a) ![]() = b
= b![]() , при b
, при b ![]() 0;
0;
б) ![]() = -b
= -b![]() , при b < 0.
, при b < 0.
Ірраціональні числа
Числа, які не можна подати у вигляді ![]() , де m ∈ Z, n ∈ N, називають ірраціональними.
, де m ∈ Z, n ∈ N, називають ірраціональними.
Наприклад, числа ![]() ,
,![]() ,
,![]() ,
, ![]() , е — ірраціональні числа.
, е — ірраціональні числа.
Запис ірраціональних чисел у вигляді десяткового дробу
Будь-яке ірраціональне число можна подати у вигляді нескінченного неперіодичного десяткового дробу. Наприклад: ![]() = 1,4142135...
= 1,4142135... ![]() = 3,1415926... е = 2,71828182...
= 3,1415926... е = 2,71828182...
Будь-який нескінченний неперіодичний десятковий дріб є записом деякого ірраціонального числа.
Дійсні числа, їх запис у вигляді десяткового дробу
Раціональні та ірраціональні числа утворюють множину дійсних чисел, яку позначають символом R. Кожне натуральне число є водночас і цілим, і раціональним, і дійсним. Кожне ціле число є також раціональним і дійсним. Наприклад: усі числа ![]() , -3, 0,
, -3, 0, ![]() , -
, -![]() — дійсні; перші три — раціональні; два останні — ірраціональні; -3, 0 — цілі.
— дійсні; перші три — раціональні; два останні — ірраціональні; -3, 0 — цілі.
Будь-яке дійсне число можна записати у вигляді нескінченного десяткового дробу.
Наприклад: ![]() = 0,5 = 0,500…,
= 0,5 = 0,500…,![]() = 0,3333…,
= 0,3333…, ![]() = 3,1622776… .
= 3,1622776… .
Будь-який нескінченний десятковий дріб є записом деякого дійсного числа
Тема 11. Рівняння, нерівності та їх системи
Рівняння з однією змінною
Рівнянням називають рівність, яка містить змінну (невідоме).
Наприклад: 2х + 3 = 0, х2 - 5х + 6 = 0 — рівняння.
Розв'язком (коренем)рівняння називається значення змінної, при підстановці якого в рівняння одержують правильну числову рівність.
Наприклад: число 2— корінь рівняння х2 - 2х = 0, бо 22 - 2 ∙ 2 = 4 - 4 = 0.
Розв’язати рівняння означає знайти його корені або довести, що їх немає.
Два рівняння є рівносильними, якщо множини їх розв’язків збігаються.
Наприклад: рівняння х + 2 = 3 і х - 1 = 0 рівносильні, оскільки вони мають спільний корінь — число 1 й інших коренів не мають.
Розв’язування будь-якого рівняння, як правило, зводиться до заміни його рівносильним рівнянням.
Основні теореми про рівносильність рівнянь
1. Якщо до обох частин рівняння додати одне й те саме число або вираз зі змінною, що не втрачає змісту за жодного її значення, то отримаємо рівняння, що є рівносильним даному.
Наприклад: рівняння х + 1 = 3 є рівносильним рівнянню х = 2, оскільки друге рівняння можна отримати з першого додаванням до обох частин першого рівняння числа -1 (або перше рівняння можна отримані з другого додаванням до обох частин другого рівняння числа 1).
2. Якщо з однієї частини рівняння перенести в другу частину доданок із протилежним знаком, то отримаємо рівняння, що є рівносильним даному.
Наприклад: рівняння х - 3 = 7 є рівносильним рівнянню х = 7 + 3, тобто рівнянню х = 10.
3. Якщо обидві частини рівняння помножити або розділити на одне й те саме число, що не дорівнює нулю, або на вираз зі змінною, який не перетворюється на нуль за жодного значення змінної і не втрачає змісту на множині допустимих значень змінної для даного рівняння, то отримаємо рівняння, що є рівносильним даному.
Наприклад: рівняння 5х = 20 є рівносильним рівнянню 5х : 5 = 20 : 5, тобто рівнянню х = 4; рівняння -![]() х = 5 є рівносильним рівнянню -
х = 5 є рівносильним рівнянню -![]() х(-2) = 5 ∙ (-2), тобто рівнянню х = -10.
х(-2) = 5 ∙ (-2), тобто рівнянню х = -10.
Приклад 1. Розв’яжіть рівняння 5х + 3(3х + 7) = 35.
Розв'язання: Спростімо рівняння: розкриємо дужки в лівій частині рівняння:
5х + 9х + 21 = 35.
Перенесемо число 21 із лівої до правої частини рівняння, змінивши знак на протилежний: 5х + 9х = 35 - 21.
Зведемо подібні члени в лівій і правій частинах рівняння: 14x = 14.
Поділимо ліву і праву частини рівняння на 14. Отже, х = 1. Відповідь: 1.
Рівняння із двома змінними
Рівність, яка містить дві змінні (невідомі), називається рівнянням із двома змінними (невідомими). Наприклад: x - у = 4, ху = 12 — рівняння із двома змінними.
Розв'язком рівняння із двома змінними називають пару значень змінних, які перетворюють це рівняння на правильну числову рівність.
Наприклад: пара чисел x = 7 і у = 3 є розв’язком рівняння 2x - 4у = 2, оскільки 2 ∙ 7 - 4 ∙ 3 = 2.
Рівняння із двома змінними, які мають одні і ті самі розв’язки, є рівносильними. Рівняння із двома змінними, які не мають розв’язків, також вважають рівносильними.
У рівнянні із двома змінними можна переносити доданки з однієї частини до другої, змінивши їх знаки. Обидві частини рівняння можна помножити на одне і те саме число або розділити на одне і те саме число, що не дорівнює нулю. При цьому отримуємо рівняння, що є рівносильним даному.
Лінійним рівнянням із двома змінними називають рівняння виду ах + by = с, де х і у — змінні, я, b, с— числа.
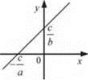 Графікам рівняння із двома змінними називають множину точок координатної площини, координат яких є розв’язками цього рівняння.
Графікам рівняння із двома змінними називають множину точок координатної площини, координат яких є розв’язками цього рівняння.
Графіком лінійного рівняння із двома змінними, у якому хоча б один із коефіцієнтів при змінних не дорівнює нулю, є пряма (рис. 1). Рис.1
Числові нерівності та їх властивості
Означення. Число а більше числа b. якщо різниця а - b є числом додатним.
Число а менше числа b. якщо різниця а - b є числом від’ємним.
Якщо а більше b, то пишуть: а > b; якщо а менше b, то пишуть: а < b.
Отже, нерівність a > b означає, що різниця а - b є додатною, тобто а - b > 0; нерівність а < b означає, що різниця а - b є від’ємною, тобто а - b < 0.
Два вирази, які сполучені знаком > або <, називають строгими нерівностями.
Знаки > і < є знаками строгої нерівності, вони протилежні один одному: якщо а > b, то b < a, і навпаки.
Окрім знаків > і <, використовують також знаки:
≥ — більше або дорівнює (не менше),
≤ — менше або дорівнює (не більше).
Нерівність а ≤ b означає, що a < b або a = b, тобто я не більше b.
Наприклад: якщо число учнів Вашого класу 30, то число я учнів, які присутні на уроці, може бути меншим або дорівнювати 30. У цьому випадку можна записати: a < 30.
Аналогічно нерівність а ≥ b означає, що а > b або а = b, тобто а не менше b.
Два вирази, які сполучені знаком ≥ або ≤, називають нестрогими нерівностями. Знаки ≥ і ≤ є знаками нестрогої нерівності.
Наведемо приклади нерівностей:
1) 5 >6; 2) 7 < 9; 3) 4 ≤ 4; 4) 4 ≥ 1;
5) 2х + 3 > 2; 6) 3х - 1 > 2x- + 1;
7) х2 + х > 3; 8) ![]() ≤ 1
≤ 1
Вираз, який стоїть ліворуч або праворуч відзнака нерівності, називають відповідно лівою чи правою частиною нерівності.
Наприклад: лівою частною нерівності х2 + х > 3 є вираз х2 + Х, а правою — число 3.
Якщо обидві частини нерівності — числа, то її називають числовою нерівністю.
Такі нерівності бувають правильні або неправильні.
Наприклад: нерівності 7 < 9; 4 ≥ 4; 4 ≥ 1 — правильні, а нерівності 5 > 6; ![]() ≤ 1 — неправильні. Теореми 1. Якщо а < b, b < с, то а < с.
≤ 1 — неправильні. Теореми 1. Якщо а < b, b < с, то а < с.
Геометрично ця властивість означає: якщо точка А (якій відповідає число а) лежить лівіше від точки В (якій відповідає число b), а точка В. у свою чергу, лежить лівіше від точки С (якій відповідає число с), тоді точка А тим більше буде лежати лівіше від точки С (рис. 2).
Аналогічно, якщо а > b, b > с, то а > с.
![]() Рис. 2
Рис. 2
Теорема 2. Якщо а < b і с — будь-яке число, то а + с < b + с.
Отже, якщо до обох частин правильної нерівності додати одне й те саме число, то отримаємо правильну нерівність.
Аналогічно: якщо а > b, с — будь-яке число, то а + с > b + с.
Наслідок. Будь-який доданок можна перенести з однієї частини нерівності в іншу, змінивши знак цього доданка на протилежний.
Теорема 3. Якщо а < b і с > 0, то ас < bс. Якщо а < b і с < 0, то ас > bс.
Аналогічно: а) якщо а > b, с > 0, то ас > bс; б) якщо а > b i с <0. то ас < bс.
Оскільки ділення можна замінити множенням на число, обернене до дільника, то аналогічні властивості є справедливими й для ділення:
а) якщо а < b і с > 0, то ![]() <
< ![]() ;
;
б) якщо а < b і с < 0, то ![]() >
> ![]() .
.
Отже, якщо обидві частини правильної нерівності намножити або поділити на одне й те саме додатне число, то отримаємо правильну нерівність. Якщо обидві частини правильної нерівності помножити або поділити на одне й те саме від'ємне число і замінити знак нерівності на протилежний, то отримаємо правильну нерівність.
Теорема 4. Якщо а > b i с > d, то а + с > b + d.
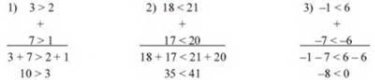 Якщо почленно додати правильні нерівності одного знака, то одержимо правильну нерівність. Наприклад:
Якщо почленно додати правильні нерівності одного знака, то одержимо правильну нерівність. Наприклад:
Теорема 5. Якщо a < b, c < d i a > 0, b > 0, c >0, d > 0, то ас < bd.
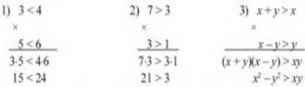 Якщо почленно перемножити правильні нерівності одного знака, ліві і праві частини яких є додатними числами, то отримаємо правильну нерівність. Наприклад:
Якщо почленно перемножити правильні нерівності одного знака, ліві і праві частини яких є додатними числами, то отримаємо правильну нерівність. Наприклад:
Слід зазначити, що теореми 4 і 5 справедливі для трьох і більше нерівностей.
Нерівності з однією змінною
Нерівністю зі змінною (невідомим) називають два вирази зі змінною (невідомим), між якими стоїть один зі знаків нерівності: > (більше), < (менше), ≥ (більше або дорівнює; не менше), ≤ (менше або дорівнює; не більше). Наприклад: 3х + 2 > 6 і х2 + х + 1 > 0 — нерівності з однією змінною.
Розв'язком нерівності з однією змінною називають значення змінної, яке перетворює нерівність в правильну числову нерівність. Наприклад: число 2 — розв’язок нерівності х + 3 > 4, а число -1 не є розв’язком даної нерівності.
Приклад 2. Доведіть, що при кожному дійсному значенні а нерівність а2 + 2 > 2а є справедливою.
Доведення: Складемо різницю лівої і правої частин нерівності й перетворимо її: а2 + 2 - 2а - а2 - 2а + 1 + 1 = (а2 - 2а + 1) + 1 = (а - 1)2 + 1. При будь-якому значенні а утворена різниця а2 + 2 - 2а — додатна, тому що значення виразу (а - 1)2 є невід’ємним, а значення виразу (а - 1 )2 + 1 — додатним. Отже, при будь-якому значенні а нерівність а2 + 2 > 2а є справедливою.
Розв’язати нерівність з однією змінною означає знайти всі її розв’язки або довести, що розв’язків немає.
Розв’язками нерівності є деяка множина чисел. У таблиці наведено деякі числові множини, їх позначення, зображення на координатній прямій і запис у вигляді нерівності.
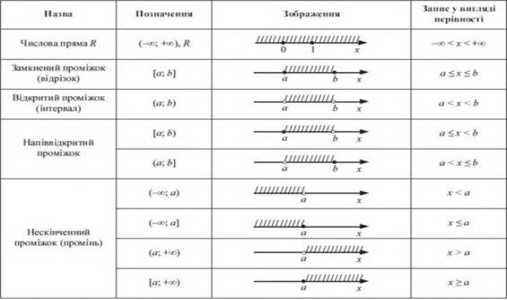
Розв’язування нерівностей, як правило, зводиться до заміни даної нерівності нерівністю, яка їй рівносильна.
Нерівності, які мають одні й ті самі розв’язки, називаються рівносильними. Нерівності, які не мають розв’язків, також вважаються рівносильними.
Нерівності з однією змінною мають такі властивості:
1. Якщо з однієї частини нерівності перенести в другу доданок із протилежним знаком, то одержимо рівносильну їй нерівність.
Наприклад: нерівність х + 2 > 3 рівносильна нерівності х + 2 - 2 > 3 - 2. тобто х > 1.
2. Якщо обидві частини нерівності помножити або поділити на одне й те саме додатне число, то отримаємо рівносильну їй нерівність.
Наприклад: ![]() х >3 рівносильна нерівності
х >3 рівносильна нерівності ![]() х ∙ 2 > 3 ∙ 2, тобто х > 6.
х ∙ 2 > 3 ∙ 2, тобто х > 6.
3. Якщо обидві частини нерівності помножити або поділити на одне й те саме від'ємне число, змінивши при цьому знак нерівності на протилежний, то одержимо рівносильну їй нерівність. Наприклад: нерівність -2х < 10 рівносильна нерівності -2х : (-2)> 10 : (-2), тобто х >-5.
Приклад 3. Розв’яжіть нерівність 2(х - 5)+ 6 ≥ 9х - 2(х - 3).
Розв'язання: Перетворімо ліву і праву частини нерівності, тобто розкриємо дужки: 2х - 10 + 6 ≥ 9х - 2х + 6. Перенесемо члени, що містять змінну до лівої частини нерівності, а члени, які не містять змінну, у праву частину нерівності, при цьому змінимо знаки членів на протилежні: 2х - 9х + 2х >10 - 6 + 6. Зведемо подібні в лівій і правій частинах нерівності: -5х ≥ 10. Поділимо обидві частини нерівності на -5, змінивши знак нерівності на протилежний: х ≤ -2. Отже, розв’язком нерівності є проміжок (-∞; -2]. Відповідь: (-∞; —2].
Системи рівнянь із двома змінними
Декілька рівнянь із двома змін ними, відносно яких поставлено завдання знайти всі спільні розв’язки, називають системою рівнянь із двома змінними. Систему рівнянь позначають зліва фігурною дужкою, що їх об’єднує. Наприклад:
![]()
![]() — системи рівнянь із двома змінними.
— системи рівнянь із двома змінними.
Розв’язати систему рівнянь із двома змінними означає знайти всі її розв’язки або довести, що система розв’язків не має.
Розв'язком системи рівнянь із двома змінними називають пару значень змінних, яка перетворює кожне рівняння системи на правильну рівність.
Наприклад: пара чисел х = 3, у = 2 (записують так (3; 2)) є розв’язком системи рівнянь ![]()
Розв’язування системи рівнянь із двома змінними, як правило, зводитеся до заміни даної системи рівносильною їй системою.
Системи рівнянь із двома змінними, які мають одні й ті самі розв’язки, називають рівносильними. Системи рівнянь, які не мають розв’язків, також вважають рівносильними.
Системи рівнянь мають такі властивості:
1. Якщо замінити порядок рівнянь заданої системи, то одержимо систему, рівносильну даній.
Наприклад: системи ![]() i
i ![]() є рівносильними.
є рівносильними.
2. Якщо одне з рівнянь системи замінити на рівносильне йому рівняння, то одержимо систему, рівносильну даній.
Наприклад: системи ![]() i
i ![]() є рівносильними.
є рівносильними.
3. Якщо в системі рівнянь з одного рівняння виразити одну змінну, наприклад у, через іншу змінну, і одержаний вираз підставити замість у в друге рівняння системи, то одержимо систему, рівносильну даній.
Наприклад: системи ![]() є рівносильними.
є рівносильними.
4. Якщо перше рівняння системи замінити сумою першого рівняння, помноженого на число а ≠ 0, і другого рівняння, помноженого на число ![]() ≠ 0, а друге рівняння залишити без змін, то одержимо систему, рівносильну даній.
≠ 0, а друге рівняння залишити без змін, то одержимо систему, рівносильну даній.
Наприклад: ![]()
![]() — є рівносильними системами.
— є рівносильними системами.
Системи нерівностей з однією змінною
Декілька нерівностей з однією змінною, відносно яких поставлено завдання знайти всі спільні розв’язки, називають системою нерівностей з однією змінною. Систему нерівностей позначають зліва фігурною дужкою, що їх об’єднує.
Наприклад: ![]()
![]() — системи нерівностей з однією змінною.
— системи нерівностей з однією змінною.
Розв’язком системи нерівностей з однією змінною називають значення змінної, при якому кожна нерівність перетворюється на правильну числову.
Наприклад: х = 3 є розв’язком системи нерівностей ![]()
Розв'язати систему нерівностей означає знайти всі її розв’язки або довести, що розв’язків немає. Розв'язування системи нерівностей з однією змінною, як правило, зводиться до заміни даної системи рівносильною їй системою.
Щоб розв’язати систему нерівностей з однією змінною слід:
- розв’язати кожну нерівність;
- знайти спільні розв’язки даних нерівностей.
Приклад 4. Розв’яжіть систему нерівностей ![]()
Розв'язання: Маємо ![]()
![]()
![]()
Зобразимо на координатній прямій множини розв’язків кожної з нерівностей (рис. 3). ![]() Рис. 3
Рис. 3
Обидві нерівності справедливі при х < -1,5. Відповідь можна записати у вигляді нерівності х < -1,5 або числового проміжку (-∞; -1,5]. Відповідь: (-∞; -1,5].
Тема 12. Функції та їхні основні властивості
Поняття функції. Способи задання функції.
Область визначення і область значень функції
Числовою функцією з областю визначення D називають залежність, згідно з якою кожному числу х із множини D відповідає за деяким правилом єдине число у із множини Е (рис. 1).
Змінну х називають незалежною змінною, або аргументам функції, а змінну у — залежною змінною, або функцією.
Функцію позначають латинськими буквами f, g, h,... (або f (x), g (x), h (x),...) або рівностями у = f(x), у = g (x), у = h (x),... .
Якщо задане конкретне значення незалежної змінної x = x0, то у0 = f(x0) називається значенням функції f у точці x0.
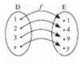 Рис. 1
Рис. 1
Наприклад: якщо f(x) = ![]() , то f(1) =
, то f(1) = ![]() =
= ![]() , f(0) =
, f(0) = ![]() = 0, f(a) =
= 0, f(a) = ![]() .
.
Область визначення функції позначають D (f) (від англ. define — визначити). Множина, що складається з усіх чисел f(x) таких, що ж належить області визначення функції f,називається областю значень функції і позначається Е (f) (від англ. exist — існувати).
Розглянемо приклад. Результати вимірювання температури тіла хворого залежно від часу подано в таблиці:
Таблиця
|
Час доби, ж (год) |
9 |
12 |
15 |
18 |
21 |
24 |
|
Температура тіла, у = f(x) (С°) |
39 |
38,5 |
38,3 |
37,3 |
37,1 |
37 |
Залежність у = f(x) є функцією, де x — незалежна змінна, у — залежна змінна.
f(9) = 39; f(12) = 38,5; f(15) = 38,3; f(18) = 37,3; f(21) = 37,1; f(24) = 37.
D(f) = {9; 12; 15; 18; 21; 24}.
E(f)= {39; 38,5; 38,3; 37,3; 37,1; 37}.
Функцію можна задати за допомогою таблиці, графіка, формули.
Найчастіше функцію задають формулою, яка дає можливість одержати значення залежної змінної у, підставивши конкретне значення аргументу x.
Наприклад: якщо кожному значенню ж із множини дійсних чисел відповідає квадрат цього числа, то функцію можна записати у вигляді формули: у = x2, або f(x) = x2.
Областю визначення функції y = f(x), яка задана формулою, називають множину тих значень, яких може набувати ж, тобто таких ж, за яких формула має зміст (усі дії, указані формулою, можна виконати). При знаходженні області визначення слід пам’ятати:
1. Якщо функція є многочленом у = аnxn + аn-1xn-1 +... + а1x + а0, то D (у) = (∞; +∞) = R. Наприклад: якщо у = x2 + 2x + 1, то D (у) = R.
2. Якщо функція має вигляд у = ![]() , де f(x) і g (x) — многочлени, то слід вважати g (x) ≠ 0 (знаменник дробу не дорівнює 0).
, де f(x) і g (x) — многочлени, то слід вважати g (x) ≠ 0 (знаменник дробу не дорівнює 0).
Наприклад: якщо у = ![]() , то x2 -1 ≠ 0. Тоді x ≠-1 і x ≠ 1. Oтже, D(у) = (∞; -1 )
, то x2 -1 ≠ 0. Тоді x ≠-1 і x ≠ 1. Oтже, D(у) = (∞; -1 )![]() (-1; 1)
(-1; 1)![]() (1;+∞).
(1;+∞).
3. Якщо функція має вигляд у = ![]() , то слід вважати f(X) ≥ 0 (арифметичний квадратний корінь існує тільки з невід’ємних чисел).
, то слід вважати f(X) ≥ 0 (арифметичний квадратний корінь існує тільки з невід’ємних чисел).
Наприклад: якщо у = ![]() , то 5 + х ≥ 0, х ≥ -5, тобто D (у) = [-5; +∞).
, то 5 + х ≥ 0, х ≥ -5, тобто D (у) = [-5; +∞).
Графік функції
Графіком функції у = f(х) називають множину всіх точок площини з координатами (х; f(х)), де перша координата «пробігає» всю область визначення функції у = f(X), а друга — це відповідні значення функції у точці х (рис. 2).
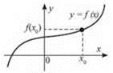 Рис. 2
Рис. 2
Зростання і спадання функції
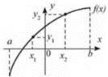 Функція у = f(х) є зростаючою (рис. 3), якщо більшому значенню аргументу відповідає більше значення функції. Тобто для будь-яких значень х1 і х2 з області визначення функції як таких, що х1 < х2, виконується нерівність f(X1) < f(х2) (або у1 < у2), і навпаки, якщо у = f(х) — зростаюча, то за умови f(x1) < f(x2) виконується нерівність x1 < x2.
Функція у = f(х) є зростаючою (рис. 3), якщо більшому значенню аргументу відповідає більше значення функції. Тобто для будь-яких значень х1 і х2 з області визначення функції як таких, що х1 < х2, виконується нерівність f(X1) < f(х2) (або у1 < у2), і навпаки, якщо у = f(х) — зростаюча, то за умови f(x1) < f(x2) виконується нерівність x1 < x2.
Рис. 3
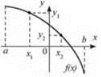 Функція у = f(х) є спадною (рис. 4), якщо більшому значенню аргументу відповідає менше значення функції. Тобто для будь-яких значень х1 і х2 з області визначення функції як таких, що х1 < х2, виконується нерівність f(х1) > f(х2) ( або у1 > у2), і навпаки, якщо у = f(х) — спадна, то за умови f(х1) > f(х2) виконується нерівність x1 < х2. Рис. 4
Функція у = f(х) є спадною (рис. 4), якщо більшому значенню аргументу відповідає менше значення функції. Тобто для будь-яких значень х1 і х2 з області визначення функції як таких, що х1 < х2, виконується нерівність f(х1) > f(х2) ( або у1 > у2), і навпаки, якщо у = f(х) — спадна, то за умови f(х1) > f(х2) виконується нерівність x1 < х2. Рис. 4
Періодичність функції
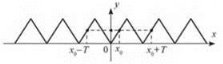 Функцію у = f(х) називають періодичною з періодом Т ≠ 0. якщо для будь-якого х з області визначення числа х + T і х - T також належать області визначення і виконується рівність: f(х + T) = f(х - T) = f(х) (рис. 5). Рис. 5
Функцію у = f(х) називають періодичною з періодом Т ≠ 0. якщо для будь-якого х з області визначення числа х + T і х - T також належать області визначення і виконується рівність: f(х + T) = f(х - T) = f(х) (рис. 5). Рис. 5
Якщо функція у = f(х) — періодична з найменшим додатним періодом Т, то функція y = f(kx + b) теж періодична, і найменший додатний період її дорівнює ![]() (k≠0).
(k≠0).
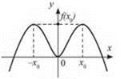 Парні та непарні функції
Парні та непарні функції
Функція у = f(х) є парною, якщо для будь-якого значення х із D (y) значення -х також належить D (у) і виконується рівність f(-х) = f(х). Графік парної функції симетричний відносно осі OY (рис. 6).
Рис. 6
Приклад 1. Чи є парною функція f(х) = х4 + х2?
Оскільки D(f) = R і f(-x) = (-х)4 + (-х)2 = х4 + х2 = f(х), то функція парна Приклад 2. Чи є парною функція f(х) = х2 +х?
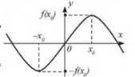 Оскільки D (f) = R, але f(-х) = (-х)2 + (-х) = х2 - х ≠ f(х), то функція не є парною.
Оскільки D (f) = R, але f(-х) = (-х)2 + (-х) = х2 - х ≠ f(х), то функція не є парною.
Функція y = f(x) є непарною, якщо для будь-якого значеннях із D (у) значення -х ∈ D(y) і виконується рівність f(-х) = -f(х). Графік непарної функції симетричний відносно початку координат (рис. 7). Рис. 7
Приклад 3. Чи є непарною функція f(х) = х3 - х5?
Оскільки D (f) = R і f(-х) = (-х)3 - (-х)5 = -х3 + x5 = -(х3 - x5) = -f(х), то функція є непарною.
Приклад 4. Чи є непарною функція f(х) = х3 - х2?
Оскільки D(f) = R i f (-х) = (-х)3 - (-х)2 = -х3 - х2 = -(х3 + х2) ≠ -f (х) = -х3 + х2, то функція не є непарною.
Графіки деяких функцій та їх основні властивості
Функція у = kх
Властивості
1. Область визначення: R.
2. Функція є непарною.
3. Для х ∈ R функція зростає, якщо k > 0 (рис. 8); спадає, якщо k < 0 (рис. 9).
4. Область значень: R.
5. Графік — пряма, що проходить через початок координат.
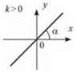
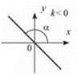
Рис. 8 Рис. 9.
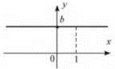
Функція у= b Властивості
Рис.10
1. Область визначення: R.
2. Функція є парною. Якщо b = 0, то функція і парна, і непарна.
3. Для х ∈ R функція стала
4. Область значень: {b}.
5. Графік — пряма, паралельна осі х, якщо b ≠ 0, і пряма що збігається з віссю x, якщо b = 0.
6. Функція періодична, будь-яке число є періодом. Найменшого додатного періода не має.
Функція y = ![]() (y =
(y = ![]() , n ∈ N, k ≠ 0)
, n ∈ N, k ≠ 0)
Властивості
1. Область визначення: х ∈ (-∞; 0) U (0; +∞).
2. Функція є непарною.
3. Якщо k > 0, функція спадає на проміжку (-∞; 0) і на проміжку (0; +∞) (рис. 11). Якщо k < 0 функція зростає на проміжку (-∞; 0) і на проміжку (0; +∞) (рис. 12).
4. Області, значень: (-∞; 0) ![]() (0; +оо).
(0; +оо).
5.Графік функції — гіпербола
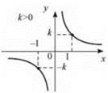 Рис. 11
Рис. 11
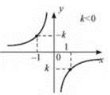
Рис. 12
Функцій y = ах2 (у = ах2n, а ≠ 0, n ∈ N)
Властивості
1. Область визначення: R.
2. Функція є парною.
3. Якщо а > 0, функція спадає на проміжку (∞; 0], зростає на проміжку [0; +∞) (рис. 13). Якщо а < 0, функція зростає на проміжку (-∞; 0], спадає на проміжку [0; +∞) (рис. 14).
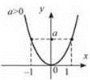
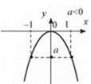
Рис. 13 Рис. 14
4. Область значень: якщо а > 0, то у ∈ [0; +∞); якщо а < 0, то у є (-∞; 0].
5. Графік функції—парабола
Функція у = aх3(у = аx2n+1, а ≠ 0, n ∈ N)
Властивості
1. Область визначення: R
2. Функція є непарною.
3. Для х ∈ R функція зростає, якщо а > 0 (рис. 15); спадає, ЯКЩO a < 0 (рис. 16).
4. Область значень: R.
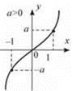 5. Графік функції — кубічна парабола.
5. Графік функції — кубічна парабола.
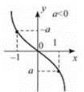
Рис. 15 Рис. 16
Функція у = |x|
Властивості
1. Область визначення: R
2. Функція є парною.
3. На проміжку (-∞; 0] функція спадає; на проміжку [0; +∞) функція зростає (рис. 17). 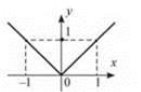 Рис. 17
Рис. 17
4. Область значень: [0; +∞).
Функція у = ![]() (y =
(y = ![]() , k ≠ 0, n ∈ N)
, k ≠ 0, n ∈ N)
Властивості
1. Область визначення: х ∈ (-∞; 0) ![]() (0; +∞).
(0; +∞).
2. Функція є парною.
3. Якщо k > 0, функція зростає для x ∈ (-∞; 0); спадає для x ∈ (0; +∞) (рис. 18); якщо k < 0, функція спадає для х ∈ (-∞; 0); зростає для x ∈(0; +∞) (рис. 19).
4. Область значень: якщо k > 0, то у ∈ (0; +∞); якщо k < 0, то у ∈ (-∞; 0).
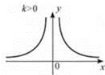
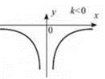
Рис. 18 Рис. 19
Функція у = ![]()
Властивості
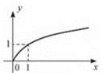 1. Область визначення: [0; +∞).
1. Область визначення: [0; +∞).
2. Функція ні парна, ні непарна
3. На проміжку [0; +∞) функція зростає (рис. 20).
4. Область значень: [0; +∞). Рис. 20
Перетворений графіків функцій
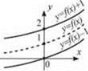 1. Щоб побудувати графік функції y = f(x + а), слід перенести графік функції f(А) уздовж осі Ох на а одиниць: вправо, якщо а < 0; вліво, якщо а > 0 (рис. 21).
1. Щоб побудувати графік функції y = f(x + а), слід перенести графік функції f(А) уздовж осі Ох на а одиниць: вправо, якщо а < 0; вліво, якщо а > 0 (рис. 21).
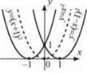
Рис. 21 Рис. 22
2. Щоб побудувати графік функції у = f(a) + b, слід перенести графік функції f(a) уздовж осі Оу на b одиниць: вверх, якщо b > 0 або вниз, якщо b < 0 (рис. 22).
 3. Щоб побудувати графік функції у = -f (х), слід графік функції y = f (х) симетрично відобразити відносно осі абсцис (рис. 23). Рис. 23
3. Щоб побудувати графік функції у = -f (х), слід графік функції y = f (х) симетрично відобразити відносно осі абсцис (рис. 23). Рис. 23
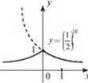
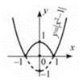
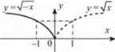 4. Щоб побудувати графік функції у = f (-х), слід графік функції у = f(х) симетрично відобразити відносно осі ординат (рис. 24). Рис. 24 5. Щоб побудувати графік функції y = |f(x)|, слід частину графіка функції y = f(x) У верхній півплощині і на осі абсцис залишити без змін, а замість частини графіка в нижній півплощині побудувати симетричну їй частину відносно осі Ох (рис. 25). Рис. 25
4. Щоб побудувати графік функції у = f (-х), слід графік функції у = f(х) симетрично відобразити відносно осі ординат (рис. 24). Рис. 24 5. Щоб побудувати графік функції y = |f(x)|, слід частину графіка функції y = f(x) У верхній півплощині і на осі абсцис залишити без змін, а замість частини графіка в нижній півплощині побудувати симетричну їй частину відносно осі Ох (рис. 25). Рис. 25
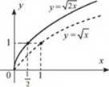 6. Щоб побудувати графік функції у = (|x|), необхідно частину графіка функції у = f(х) у правій півплощині і на осі ординат залишити без змін, а замість частини в лівій півплощині побудувати симетричну тій, що в правій частині відносно осі Оу (рис. 26). Рис. 26
6. Щоб побудувати графік функції у = (|x|), необхідно частину графіка функції у = f(х) у правій півплощині і на осі ординат залишити без змін, а замість частини в лівій півплощині побудувати симетричну тій, що в правій частині відносно осі Оу (рис. 26). Рис. 26
7. Щоб побудувати графік функції у = f(kх), k >0, слід:
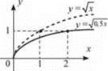 1) при k > 1 стиснути графік функції у = f (х) до точки (0; 0) уздовж осі абсцис у k разів (рис. 27); Рис. 27
1) при k > 1 стиснути графік функції у = f (х) до точки (0; 0) уздовж осі абсцис у k разів (рис. 27); Рис. 27
2) при 0 < k < 1 розтягнути від точки (0; 0) графік функції y = f(x) уздовж осі абсцис у ![]() разів (рис. 28). Рис. 28
разів (рис. 28). Рис. 28
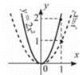 8. Щоб побудувати графік функції у = kf (x), k > 0, слід:
8. Щоб побудувати графік функції у = kf (x), k > 0, слід:
1) при k > 1 розтягнути графік функції у = f(x) від точки (0; 0) уздовж осі ординат у k разів (рис. 29); Рис. 29
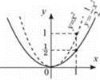 2) при 0 < k < 1 стиснути графік функції у = f(x) до точки (0; 0) уздовж осі ординат у
2) при 0 < k < 1 стиснути графік функції у = f(x) до точки (0; 0) уздовж осі ординат у ![]() разів (рис. 30). Рис. 30
разів (рис. 30). Рис. 30
Функція, обернена до даної
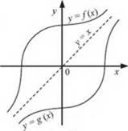 Функцію, яка набуває кожного свого значення в єдиній точці області визначення, називають оборотною.
Функцію, яка набуває кожного свого значення в єдиній точці області визначення, називають оборотною.
Наприклад: функція у = 2x + 1 — оборотна, а функція у = x2 (визначена на всій числовій осі) не є оборотною. Рис. 31
Якщо функція задана формулою у = f(х), то для знаходження оберненої функції потрібно розв’язати рівняння f(x) = у відносно х, а потім поміняти місцями x і у.
Наприклад: оберненою до функції у = 2x + 1 є функція у = ![]() .
.
Якщо рівняння f(x) = у відносно має більше ніж один корінь, то функція y = f(x) не має оберненої функції.
Наприклад: функція у = х2 + 1 оберненої функції не має.
Графіки даної функції і оберненої до неї симетричні відносно прямої у = х (рис. 31).
Наприклад: функції у = 2х + 1 і у = ![]() , графіки яких симетричні відносно прямої у = х, є оберненими (рис. 32).
, графіки яких симетричні відносно прямої у = х, є оберненими (рис. 32).
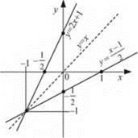 Якщо функція у = f(x) (рис. 31) зростає (спадає) на деякому проміжку, то вона оборотна. Функція, яка обернена до даної і визначена в області значень функції у = f(x), також є зростаючою (спадною).
Якщо функція у = f(x) (рис. 31) зростає (спадає) на деякому проміжку, то вона оборотна. Функція, яка обернена до даної і визначена в області значень функції у = f(x), також є зростаючою (спадною).
Якщо функція у = f(x) визначена на області визначення D і має область значень Е, то обернена функція має область визначення Е і область значень D. Рис. 32
Тема 13. Лінійна функція, рівняння, нерівності та їх системи.
Лінійна функція y = kх + b
Лінійною називають функцію виду у = kх + b, де k і b — дійсні числа Основні властивості лінійних функцій подано в таблиці.
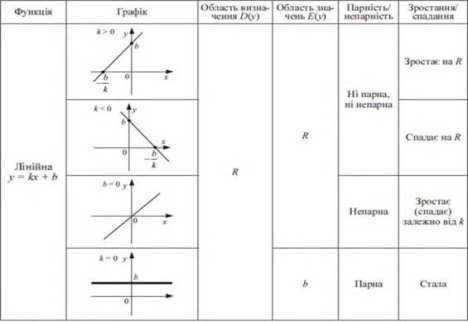
Лінійне рівняння з однією змінною
Лінійним рівнянням з однією змінною називають рівняння виду ах = b, де х — змінна, а і b — числа.
Якщо а ≠ 0, то рівняння ах = b має єдиний корінь х = ![]() .
.
Наприклад: рівняння 5х = 6 має корінь х = 1,2.
Якщо а = 0, b ≠ 0, то рівняння ах = b не має коренів.
Наприклад: рівняння 0x- = 5 не має коренів.
Якщо а = 0, b = 0, то коренем рівняння ах = b є будь-яке число.
Деякі рівняння зводяться до розв’язування лінійних рівнянь. Розгляньмо приклади.
Приклад 1. Розв’яжіть рівняння 2 - ![]() +
+ ![]() = 0.
= 0.
Розв'язання
Щоб позбутися знаменників дробів, помножимо кожний член рівняння на найменший спільний знаменник дробів, тобто на 20, і отримаємо:
2 ∙ 20 - ![]() ∙
∙ ![]() +
+ ![]() ∙
∙ ![]() = 0 ∙ 20, 40 – 5(3x - 4) + 4(x+18) = 0.
= 0 ∙ 20, 40 – 5(3x - 4) + 4(x+18) = 0.
Розкриємо дужки: 40 - 15x + 20 + 4X + 72 = 0.
Залишимо члени зі змінними в лівій частині рівняння, а члени без змінних перенесемо в праву частину (змінивши знаки членів на протилежні):
-15x + 4а = -40 - 20 - 72.
Зведемо подібні доданки: -11X = -132, звідси x = -132 : (-11), x = 12. Відповідь: 12.
Приклад 2. Розв’яжіть рівняння (2X - 6)(X + 2) = 0.
Розв’язання: Якщо добуток кількох множників дорівнює нулю, то хоча б один із множників дорівнює нулю. Скористаємося цим фактом при розв’язуванні даного рівняння.
Ліва частина рівняння —добуток невідомих множників 2x - 6 і x + 2, а права частина— нуль. Щоб розв’язати це рівняння, досить прирівняти до нуля множники 2x - 6 і x + 2 та розв’язати отримані рівняння. Отже, 2x - 6 = 0 або а + 2 = 0, тоді 2а - 6 = 0, 2x = 6, x = 6 : 2, x = 3 або x + 2 = 0, x = -2. Відповідь: 3; -2.
Приклад3. Розв’яжіть рівняння |2x + 3| = 1.
Розв’язання: Згадаймо означення модуля:
|x| = ![]()
Із точки зору геометрії |а| означає відстань від точки а, зображеної на координатній прямій, до початку координат (точки 0).
1- й спосіб. Якщо 2x + 3 < 0, то за означенням модуля - (2X + 3) = 1, тоді 2X + 3 = -1, 2X = -3 - 1,2X = - 4, x = -2. Якщо 2X + 3 ≥ 0, то за означенням модуля 2X + 3 = 1, тоді 2X + 3 = 1,2X = -3 + 1,2X = -2, x = -1. Відповідь: -1; -2.
2- й спосіб. Ураховуючи геометричний зміст модуля, рівність |2х + 3| = 1 означає, що відстань від точки 2X + 3 до початку координат дорівнює числу 1 (рис. 1), тобто
![]()
Рис. 1
1) 2х + 3 = -1,2x = -3 - 1,2х = -4,х = -2;
2) 2х + 3 = 1,2х = -3 + 1, 2х =-2,x = -1. Відповідь: -1; -2.
Лінійні нерівності з однією змінною
Нерівності виду ах > b, ах < b, ах ≥ b, ах ≤ b, де а, b — деякі числа ах—змінна, називають лінійними нерівностями з однією змінною.
Розглянемо нерівність ах > b.
1. Якщо а > 0, то х > ![]() . Наприклад: 3х > 6, х > 2.
. Наприклад: 3х > 6, х > 2.
2. Якщо а < 0, то х < ![]() . Наприклад: -2х > 4, х < -2.
. Наприклад: -2х > 4, х < -2.
3. Якщо а = 0, b < 0, то розв’язком нерівності є множина всіх дійсних чисел R.
Наприклад: 0х > - 5, х ∈ R.
4. Якщо а = 0, b > 0, то нерівність розв’язків не має.
Наприклад: нерівність 0х > 5 не має розв’язків.
Розглянемо нерівність ах < b.
1. Якщо a > 0, то х< ![]() . Наприклад:
. Наприклад: ![]() х < 6, х < 12.
х < 6, х < 12.
2. Якщо а < 0, то х > ![]() . Наприклад: -
. Наприклад: -![]() х < 6, х > -12.
х < 6, х > -12.
3. Якщо а = 0, b < 0, то нерівність розв’язків не має.
Наприклад: нерівність 0х < - 5 розв’язків не має.
4. Якщо а = 0, b > 0, то розв’язком нерівності є множина всіх дійсних чисел R.
Наприклад: нерівність 0х < 5, х ∈ R.
У рівнянні, крім невідомого, яке потрібно знайти, можуть бути введені й інші букви.
Наприклад: ах = 3 - а, (n + 2)х = 2 + (n + 2).
Розгляньмо рівняння ах = 3 - а. яке залежно від значення змінної а матиме вигляд:
2х = 3 - 2, якщо а = 2;
0х = 3 - 0, якщо а = 0;
3х = 3 - 3, якщо а = 3 і т. д.
Змінну, яку потрібно знайти, будемо називати невідомою, іншу змінну — параметрам.
Розв'язати рівняння з параметром означає, що для кожного значення параметра треба встановити. чи має рівняння розв'язки, і якщо має, то знайти ці розв'язки, що, як правило, залежать від параметра. Розгляньмо приклади.
Приклад 4. Розв’яжіть рівняння х + 5 = а + 6 відносно х.
Розв’язання
Перетворивши рівняння, отримаємо х = а + 1.
Рівняння має єдиний розв’язок незалежно від значення параметра. Отже, х = а + 1.
Відповідь: а + 1.
Приклад 5. Розв’яжіть рівняння (а - 1 )х = 3 відносно х.
Розв'язання
Якщо а - 1 ≠ 0, тобто а ≠ 1, то рівняння має єдиний корінь х = ![]() .
.
Якщо а - 1 = 0, тобто а = 1, то рівняння набуває вигляду 0х = 3 і не має коренів.
Відповідь: при а ф 1 дане рівняння має єдиний корінь х = ![]() , а при а = 1 — коренів не має.
, а при а = 1 — коренів не має.
Приклад 6. Розв’яжіть нерівність х - ![]() ≥
≥ ![]() .
.
Розв’язання
Помножимо обидві частини нерівності на 4:
4x - ![]() ∙
∙ ![]() ≥
≥ ![]() ∙
∙ ![]() , 4x – 2(x+3)≥2x – 1.
, 4x – 2(x+3)≥2x – 1.
Розкриємо дужки в лівій частині нерівності: 4х - 2х - 6 > 2х - 1. Перенесемо члени нерівності зі змінними в ліву частину нерівності, а члени без змінних —у праву частину (змінивши знаки членів, які переносимо, на протилежні): 4х - 2х - 2х ≥ - 1 + 6, звідси маємо 0х ≥ 5. Отже, дана нерівність розв’язків не має.
Відповідь: нерівність розв’язків не має.
Системи лінійних рівнянь із двома змінними
Системи рівнянь розв’язують кількома способами: графічним, підстановки, додавання.
Розгляньмо приклади.
Приклад 7. Розв’яжіть систему рівнянь ![]() графічним способом.
графічним способом.
Розв’язання
Побудуємо графіки рівнянь х + у = 5 або у = -х + 5 (пряма, яка проходить через точки (0; 5) і (5; 0)) та х - у = 1 або у = х - 1 (пряма, яка проходить через точки (0; -1) та (1; 0)) (рис. 2).
 Ці графіки перетинаються в точці (3; 2).
Ці графіки перетинаються в точці (3; 2).
Отже, розв’язком системи є пара чисел (3; 2).
Відповідь: (3; 2). Рис. 2
Щоб розв’язати систему рівнянь графічним способом, треба:
1) виконати рівносильні перетворення системи так, щоб було зручно побудувати графіки рівнянь системи;
2) побудувати графіки;
3) знайти координати точок (точки) перетину побудованих ліній. Ці координати і є розв'язками (розв'язком) системи рівнянь.
Зауваження. Графічний спосіб розв’язування систем рівнянь не є універсальним, оскільки не завжди розв’язком системи є пара цілих чисел. Іноді важко точно встановити координат точки перетину побудованих графіків функцій, можливо вказати лише наближені значення. Тому, як правило, використовують алгебраїчні способи розв’язування систем рівнянь: спосіб підстановки, додавання.
Приклад 8. Розв’яжіть систему рівнянь ![]() способом підстановки.
способом підстановки.
Розв'язання
Із першого рівняння системи виразимо у через х: у = 6 - 2х. Одержаний вираз підставимо в друге рівняння системи:
4х - 3 ∙ (6 - 2x) = 2, звідси 4x - 18 + 6х = 2; 10x = 20; х = 2.
Одержане значення х підставляємо у вираз у = 6 - 2х;
у = 6 - 2 ∙ 2 = 2.
Отже, пара (2; 2) - розв’язок даної системи.
Відповідь: (2; 2).
Способом підстановки систему двох рівнянь із двома змінними розв’язують за таким порядком:
1) з одного рівняння системи виражаємо одну зі змінних через другу змінну і відомі величини;
2) знайдене значення підставляємо в друге рівняння системи, одержуємо рівняння відносно другої змінної;
3) розв'язуємо одержане рівняння і знаходимо значення цієї змінної;
4) підставляючи знайдене значення у вираз для першої змінної, одержуємо відповідне її значення;
5) записуємо відповідь.
Зауваження. Спосіб підстановки, як правило, використовують, якщо коефіцієнт при одній зі змінних в одному з рівнянь системи дорівнює 1.
Приклад 9. Розв’яжіть систему рівнянь ![]() способом додавання.
способом додавання.
Розв'язання
Помножимо почленно перше рівняння системи на 3, а друге — на 2 (це дає змогу при додаванні рівнянь позбавитися від змінної у):

Додавши почленно рівняння, одержуємо 19x = 19, звідси х = 1 (значення у знайдемо з першого рівняння системи: 3 ∙ 1 + 2у = 5, 2у = 2, у = 1, отже, (1; 1) — розв’язок системи).
Значення у можна знайти, якщо помножимо почленно перше рівняння на -5, а друге — на 3: 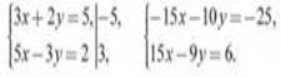 Додавши почленно рівняння, одержуємо:
Додавши почленно рівняння, одержуємо:
-19у = -19, у= 1. Отже, пара(1; 1) є розв’язком даної системи. Відповідь: (1; 1).
Розв’язування системи двох лінійних рівнянь із двома змінними способом алгебраїчного додавання виконують за таким порядком:
1)урівнюємо коефіцієнти при одній зі змінних шляхом почленного множення обох рівнянь на множники, підібрані відповідним чином:
2) додаючи (або віднімаючи) почленно рівняння системи, виключаємо одну зі змінних:
3) розв'язуємо одержане рівняння з однією змінною;
4) значення другої змінної можна знайти таким же способом (або підстановкою знайденого значення змінної в будь-яке із заданих рівнянь системи);
5) записуємо відповідь.
Зауваження. Спосіб додавання, як правило, використовують, якщо коефіцієнти при одній зі змінних у рівнянні системи — протилежні числа.
Системи лінійних нерівностей з однією змінною
Розглянемо приклади розв’язування систем нерівностей.
Приклад 10. Розв’яжіть систему нерівностей ![]() Розв'язання
Розв'язання
Маємо ![]()
![]()
![]()
Зображаємо на числовій прямій множини розв’язків кожної з нерівностей (рис. 3). ![]() Рис. 3 Обидві нерівності справедливі при х ≤ -1,5. Відповідь можна записати у вигляді нерівності х ≤-1,5 або у вигляді числового проміжку (-∞; -1,5].
Рис. 3 Обидві нерівності справедливі при х ≤ -1,5. Відповідь можна записати у вигляді нерівності х ≤-1,5 або у вигляді числового проміжку (-∞; -1,5].
Відповідь: (-∞; -1,5].
Приклад 11. Розв’яжіть систему нерівностей ![]()
Розв'язання: Маємо ![]()
![]()
Використовуючи числову пряму, знайдемо спільні розв’язки нерівностей
х > ![]() і х >
і х > ![]() (рис. 4).
(рис. 4). ![]() Рис. 4
Рис. 4
Бачимо, що множина розв’язків системи складається із чисел, які задовольняють умові х > ![]() , тобто є числовим проміжком (
, тобто є числовим проміжком (![]() ;+∞). Відповідь: (
;+∞). Відповідь: (![]() ;+∞).
;+∞).
Приклад 12. Розв’яжіть систему нерівностей ![]()
Розв'язання: Маємо ![]()
![]()
![]()
Використовуючи числову пряму (рис. 5), знаходимо, що спільних розв’язків нерівності х > 0 і х < - 0,2 не мають. Отже, дана система розв’язків не має.
![]() Рис. 5 Відповідь: розв’язків не має.
Рис. 5 Відповідь: розв’язків не має.
Приклад 13. Розв’яжіть систему нерівностей ![]()
Розв’язання
Маємо ![]()
![]()
![]()
Розв’язком першої і другої нерівностей є числова пряма (-∞; +∞). Отже, розв’язком даної системи є будь-яке число х. Відповідь: (-∞; +∞).
Приклад 14. Розв’яжіть нерівність (а - 3)(2 - а) > 0.
Розв'язання
Добуток двох множників невід’ємний, коли обидва множники або невід’ємні, або недодатні. Тому розв’язування даної нерівності зводиться до розв’язування двох систем нерівностей: ![]() або
або ![]() Тоді маємо:
Тоді маємо: ![]() або
або ![]()
Оскільки перша система не має розв’язків, а розв’язком другої системи є проміжок [2; 3], то дана система має множину розв’язків — [2; 3].
Відповідь: [2; 3].
Приклад 15. Розв’яжіть нерівність ![]() < 0.
< 0.
Розв'язання: Дріб від’ємний, коли значення чисельника і знаменника мають протилежні знаки, тому розв’язування даної нерівності зводиться до розв’язування двох систем нерівностей: ![]() або
або ![]() Тоді маємо:
Тоді маємо: ![]() або
або ![]() Оскільки друга система не має розв’язків, а розв’язком першої системи є проміжок (-1; 1), то дана система має множину розв’язків — (-1; 1). Відповідь: (-1; 1).
Оскільки друга система не має розв’язків, а розв’язком першої системи є проміжок (-1; 1), то дана система має множину розв’язків — (-1; 1). Відповідь: (-1; 1).
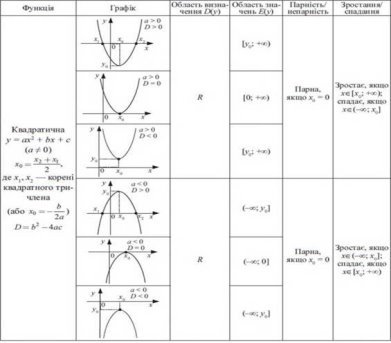 Тема 14. Квадратична функція, рівняння, нерівності та їх системи
Тема 14. Квадратична функція, рівняння, нерівності та їх системи
Квадратична функція у = ах2 + bх + с
Квадратичною називають функцію виду у = ах2 + bх + с; де а, b, с — дійсні числа, причому а ≠ 0. Основні властивості квадратичних функцій подано в таблиці.
Таблиця 1
Квадратне рівняння
Квадратним називають рівняння виду ах + bх + с = 0, де х — змінна; а, b, с — числа, причому а ≠ 0. Число а називають першим (старшим) коефіцієнтом, b — другим коефіцієнтом, с — вільним членом.
Квадратне рівняння, у якого перший коефіцієнт дорівнює числу 1, називають зведеним квадратним рівнянням.
Квадратне рівняння, у якого хоча б один із коефіцієнтів — b або с — дорівнює нулю, називають неповним квадратним рівнянням.
Неповне квадратне рівняння ваду ах2 + bх = 0
Рівняння виду ах2 + bх = 0 завжди має два корені: 0 і -![]() .
.
Такі рівняння, як правило, розв’язують розкладанням його лівої частини на множники. Наприклад: 5х2 - 15х = 0; 5х(х - 3) = 0. х1 = 0 і х2 = 3.
Неповне квадратне рівняння виду ах2 + с = 0
Якщо -![]() > 0. то рівняння виду ах2 + с = 0 має два корені: -
> 0. то рівняння виду ах2 + с = 0 має два корені: - ![]() та
та ![]() .
.
Наприклад: 4х2 - 9 = 0; 4х2 = 9, х2 = ![]() , x1 =
, x1 = ![]() i x2 = -
i x2 = -![]() , тобто х1 = 1
, тобто х1 = 1![]() і х2 = -1
і х2 = -1![]() .
.
Якщо -![]() < 0, то рівняння виду ах2 + с = 0 не має коренів. Наприклад: 4х2 + 9 = 0, х2 = -
< 0, то рівняння виду ах2 + с = 0 не має коренів. Наприклад: 4х2 + 9 = 0, х2 = -![]() коренів немає. Якщо -
коренів немає. Якщо -![]() = 0. то рівняння виду ах2 + с = 0 має один корінь: х = 0.
= 0. то рівняння виду ах2 + с = 0 має один корінь: х = 0.
Формула коренів квадратного рівняння
Вираз D = b2 - 4ас називають дискримінантом квадратного рівняння ах2 + bх + с = 0.
Якщо D > 0, то квадратне рівняння має два корені; якщо 0 = 0 — то один корінь; якщо D < 0, то квадратне рівняння коренів не має.
Корені квадратного рівняння ах2 + bх + с = 0 при D ≥ 0 знаходять за формулою
x1,2 = ![]() .
.
Для квадратного рівняння виду ах2 + 2kх + с = 0 формула коренів має вигляд
x = ![]() .
.
Для зведеного квадратного рівняння виду х2 + рх + q = 0 формула коренів має вигляд x1,2 = ![]()
![]()
![]() -q.
-q.
Квадратний тричлен
Квадратним тричленом називають многочлен виду ах2 + bх + с, де х — змінна; а, b, с — деякі дійсні числа, причому а ≠ 0.
Наприклад: вирази 3х2 - х + 5; х2 - 3х + 4; х2 + 1 — квадратні тричлени.
Коренем квадратного тричлена називають значення змінної, при якому значення цього тричлена дорівнює нулю.
Наприклад: коренем тричлена 3х2 - 2х - 5 є число -1, бо при х = -1 маємо 3 ∙ (-1)2 - 2 ∙ (-1) - 5 = 0. Квадратний тричлен ax2 + bx+ с має не більше двох коренів:
1) якщо D = b2 - 4ас < 0, то квадратний тричлен не має коренів;
2) якщо D = b2 - 4ас = 0, то квадратний тричлен має два рівних корені x1 = х2 = ![]() ;
;
3) якщо D = b2 - 4ас > 0, то квадратний тричлен має два різних корені x1,2 = ![]() .
.
Число D = b2 - 4ас називають дискримінантам квадратного тричлена.
Теореми Biєта
Якщо х1 і х2 — корені квадратного тричлена ах2 + bх + с, то виконуються рівності x1 + x2 = -![]() та x1 ∙ x2 =
та x1 ∙ x2 = ![]() .
.
Розкладання квадратного тричлена на множники
Якщо D = b2 - 4ас > 0, то виконується рівність
ах2 + bх + с = а(х - x1)(х – х2), де x1 і х2 — корені квадратного тричлена.
Доведення: Згідно з теоремою Вієта маємо x1 + х2 =-![]() , x1x2 =
, x1x2 = ![]() .
.
Тоді ах2 + bх + с = a(x22 + ![]() x +
x + ![]() ) = а(х2 - (х1 + х2 )х + х1х2 )=
) = а(х2 - (х1 + х2 )х + х1х2 )=
= а(х2 - x1x - х2х + x1x2) = а (х(х - x1) - х2 (х - x1)) = a(х - x1)(х - х2).
Якщо D = b2 - 4ас = 0, то виконується рівність ах2 + bх + с = а(х - х1)2. Якщо D = b2 - 4ас < 0, то квадратний тричлен не можна розкласти на лінійні множники у множині дійсних чисел.
Розв'язування нерівностей другого степеня з однією змінною
Нерівність, лівою частиною якої є квадратний тричлен ах2 + bх + с, де а ≠ 0; b, с — дані числа, а правою — нуль, називають квадратною.
Наприклад: нерівності х2 - 5х + 3 < 0; х2 - 3х + 2 ≤ 0; 2х2 - 3х + 2 ≥ 0; 3х2 - 2х + 1 > 0 є квадратними, або нерівностями друг ого степеня з однією змінною.
Розв’язати нерівність другого степеня з однією змінною означає знайти всі її розв’язки або довести, що їх немає. Під час розв’язування квадратної нерівності знаходять проміжки, у яких відповідна квадратична функція набуває додатних, від’ємних, недодатних, невід’ємних значень.
Приклад 1. Розв’яжіть нерівність х2 + 2х - 48 < 0.
Розв'язання
Графік функції у = х2 + 2х - 48 — парабола, вітки якої напрямлені вгору. Знайдемо нулі функції, для цього розв’яжемо рівняння х2 + 2х - 48 = 0. Корені цього рівняння дорівнюють x1,2 = ![]() =
= ![]() ; x1 = 6 i x2 = -8.
; x1 = 6 i x2 = -8.
Отже, парабола перетинає вісь х у двох точках, абсциси яких дорівнюють -8 і 6.
На рис. 1 видно, що функція набуває від’ємних значень, коли х належить проміжку (-8; 6). Значить, розв’язком нерівності х2 + 2х - 48 < 0 є числовий проміжок (-8; 6).
Відповідь: (-8; 6).
На рис. 1 видно, що:
1) розв’язками нерівності х2 + 2х - 48 ≤ 0 є всі числа проміжки [-8; 6];
2) розв’язками нерівності х2 + 2х - 48 > 0 є всі числа проміжків (-∞; -8) або (6; +∞), тобто об’єднання проміжків (-∞; -8)![]() (6; +∞);
(6; +∞);
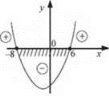 3) розв’язками нерівності х2 + 2х - 48 ≥ 0 є об’єднання проміжків (-∞;-8]
3) розв’язками нерівності х2 + 2х - 48 ≥ 0 є об’єднання проміжків (-∞;-8]![]() [6; +∞).
[6; +∞).
Приклад 2. Розв’яжіть нерівність 25х2 + 30х + 9 > 0.
Рис. 1
Розв'язання
Розглянемо функцію у = 25х2 + 30х + 9 = (5х + 3)2. Її графік — парабола, вітки якої напрямлені догори (рис. 2). Розв’яжемо рівняння (5х + 3)2 = 0, звідси х = -0,6. Рівняння має єдиний корінь. Отже, парабола дотикається осі ОХ. На рис. 2 видно, що функція набуває додатних значень при будь-яких х, окрім - 0,6.
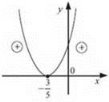 Відповідь: (-∞; - 0,6)
Відповідь: (-∞; - 0,6)![]() (- 0,6; + ∞).
(- 0,6; + ∞).
Із рис. 2 випливає також, що:
1) розв’язком нерівності 25х2 + 30х + 9 ≥ 0 є всі дійсні числа;
2) нерівність 25х2 + 30х + 9 ≤ 0 має один розв’язок: х = -0,6; Рис. 2
3) нерівність 25x2 + 30х + 9 < 0 розв’язків не має.
Приклад 3. Розв’яжіть нерівність -х2 + х - 1 < 0.
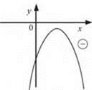 Розв'язання Рис.3
Розв'язання Рис.3
Графік функції у = -х2 + х - 1 — парабола, вітки якої напрямлені вниз. Рівняння -х2 + х - 1 =0 дійсних коренів не має, тому парабола не перетинає вісь ОХ. Отже, вона розташована нижче осі ОХ (див. рисунок 3). Це означає, що значення квадратичної функції при всіх х — від’ємні, тобто нерівність -х2 + х - 1 < 0 виконується при всіх дійсних числах (-∞; +∞).
Відповідь: (-∞; +∞).
На рис. З видно також, що:
1) розв’язками нерівності -х2 + х - 1 < 0 є множина всіх дійсних чисел R:
2) нерівності -х2 + х - 1 > 0 та -х2 + х - 1 ≥ 0 розв’язків не мають.
Із розглянутих прикладів можна зробити висновок, що для розв’язування квадратних нерівностей за допомогою графіків треба:
1) визначити напрям вітів параболи за знаком першого коефіцієнта квадратичної функції у = ах2 + bх + с (якщо а > 0, то вітки параболи напрямлені догори, якщо а < 0, то вниз);
2) знайти дійсні корені квадратного рівняння ах2 + bх + с = 0 або встановити, що їх немає;
3) схематично побудувати графік квадратичної функції, використовуючи точки перетину (точки дотику) із віссю ОХ, якщо вони є;
4) за графіком визначити проміжки, на яких функція набуває значень, при яких виконується задана нерівність.
Квадратні нерівності можна розв'язувати методом інтервалів.
Розв’язування квадратичних нерівностей методом інтервалів Розглянемо розв’язування квадратичних нерівностей методом інтервалів на прикладі.
Приклад 1. Знайдіть, при яких значеннях х квадратний тричлен х2 - 5х + 6 набуває додатних значень, а при яких — від’ємних.
Розв'язання: Розкладемо квадратний тричлен х2 - 5х + 6 на множники
х2 - 5х + 6 = (х - 2)(х - 3).
Точки х = 2 і х = 3 (див. рис. 4) поділяють числову пряму на три проміжки: (-∞; 2); (2; 3); (3; +∞).![]() Рис. 4 Вираз (х - 2)(х - 3) є добутком двох множників. Знак кожного з цих множників та їх добутку подамо у вигляді табл. 2.
Рис. 4 Вираз (х - 2)(х - 3) є добутком двох множників. Знак кожного з цих множників та їх добутку подамо у вигляді табл. 2.
Таблиця 2
|
Проміжки \Множники |
(-∞; 2) |
(2; 3) |
(3; +∞) |
|
х - 2 |
|
+ |
+ |
|
х - 3 |
|
|
+ |
|
(х - 2)(х - 3) |
+ |
- |
+ |
Рухаючись уздовж числової осі зліва направо, ми бачимо, що на проміжку (-∞; 2) квадратний тричлен х2 - 5х + 6 = (х - 2)(х - 3) набуває додатних значень, оскільки в цьому випадку обидва множники х - 2 і х - 3 є від’ємними.
На проміжку (2; 3) цен тричлен набуває від’ємних значень і, отже, при переході через точку х = 2 змінює знак. Це відбувається тому, що в добутку (х - 2)(x - 3) при переході через точку х = 2 перший множник х - 2 змінює знак, а другий множник х - 3 — ні.
При переході через точку x = 3 тричлен знову змінює знак, оскільки в добутку (х - 2)(х - 3) перший множник х - 2 не змінює знак, а другий множник х - 3 змінює.
Отже, рухаючись уздовж числової прямої, ми спостерігаємо, як змінюється знак добутку (х - 2)(x - 3).
Таким чином, задачу про знак квадратного тричлена х2 - 5х + 6 можна розв’язати у такий спосіб.
Позначити на числовій прямій корені рівняння x2 - 5х + 6 = 0, тобто точки х = 2, х = 3. Вони поділяють числову пряму (рис. 5) на три проміжки. На проміжку (-∞; 2) значення тричлена х2 - 5х + 6 додатне, тому розставляємо його знаки на останніх проміжках, ураховуючи чергування знаків.
Рис. 5![]()
На рис. 5 видно, що x2 - 5x + 6 > 0 на проміжку (-∞; 2)![]() (3; +∞), а на проміжку (2; 3) - x2 - 5x + 6 < 0.
(3; +∞), а на проміжку (2; 3) - x2 - 5x + 6 < 0.
Приклад 2. Розв’яжіть нерівність 2X2 - 3X - 5 ≥ 0.
Розв'язання
Знайдемо корені квадратного тричлена 2x2 - 3х - 5:
х1,2 = ![]() =
= ![]() ; х1 =
; х1 = ![]() = 2
= 2![]() ; х2 = -1.
; х2 = -1.
Наносимо на числову пряму точки -1 і 2![]() , які поділяють її на три проміжки (див. рис. 6). Визначаємо знак тричлена 2x2 - 3х - 5 на проміжку (∞; -1), він на цьому проміжку додатний. Знаходимо знаки тричлена на інших проміжках.
, які поділяють її на три проміжки (див. рис. 6). Визначаємо знак тричлена 2x2 - 3х - 5 на проміжку (∞; -1), він на цьому проміжку додатний. Знаходимо знаки тричлена на інших проміжках.
![]() Рис. Отже, 2x2 - 3x - 5 ≥ 0, якщо ,х належить об’єднанню проміжків (-оо; -1]
Рис. Отже, 2x2 - 3x - 5 ≥ 0, якщо ,х належить об’єднанню проміжків (-оо; -1] ![]() 2
2![]() ;+∞). Відповідь: (-∞; -1]
;+∞). Відповідь: (-∞; -1]![]() (2
(2![]() ;+∞).
;+∞).
Тема 15. Раціональні рівняння, нерівності та їх системи
Рівняння зі змінною в знаменнику
Рівняння ![]() = 0 є рівносильним системі рівнянь
= 0 є рівносильним системі рівнянь ![]()
Приклад 1. Розв’яжіть рівняння ![]() = 0.
= 0.
Розв’язання
![]() = 0;
= 0; ![]()
![]()
Отже, х = -3. Відповідь: -3.
Раціональні рівняння
Рівняння f(х) = g (х) називається раціональний, якщо f(х) і g (х) — раціональні вирази.
Щоб розв’язати раціональне рівняння, потрібно:
1) знайти спільний знаменник усіх дробів, що входять до рівняння:
2) замінити дане рівняння цілим, помноживши обидві його частини на спільний знаменник:
3) розв'язати одержане ціле рівняння:
4) виключити з коренів цілого рівняння ті, які перетворюють на нуль спільний знаменник.
Приклад 2. Розв’яжіть рівняння 1 + ![]() -
- ![]() =
= ![]() .
.
Рoзв'язання
1 + ![]() -
- ![]() =
= ![]() ; 1 ∙ (x2-1) +
; 1 ∙ (x2-1) + ![]() ∙
∙ ![]() -
- ![]() ∙
∙ ![]() =
= ![]() ∙
∙ ![]() ;
;
![]()
![]()
![]()
![]()
Отже, х = 2.
Відповідь: 2.
Дробові нерівності
Нерівність ![]() > 0 рівносильна двом системам
> 0 рівносильна двом системам ![]() або
або ![]()
Нерівність ![]() < 0 рівносильна двом системам
< 0 рівносильна двом системам ![]() або
або ![]()
Нерівність ![]() ≥ 0 рівносильна двом системам
≥ 0 рівносильна двом системам ![]() або
або ![]()
Нерівність ![]() ≤ 0 рівносильна двом системам
≤ 0 рівносильна двом системам ![]() або
або ![]()
Приклад 3. Розв’яжіть нерівність ![]() < 0.
< 0.
Розв'язання ![]() < 0;
< 0; ![]() або
або ![]() тоді
тоді ![]() або
або ![]()
Звідси х∈(7; +∞) (рис. 1) або х∈(-∞; 2) (рис. 2).
![]()
![]()
Рис. 1 Рис. 2 Отже, x∈(-∞; 2)![]() (7; +∞).
(7; +∞).
Відповідь: (-∞; 2 )![]() ( 7; =∞).
( 7; =∞).
Розв'язування раціональних нерівностей методом інтервалів
Щоб розв’язати нерівність f(x) > 0 (f(x) < 0, f(x) ≥ 0, f(x) ≤ 0), де f(x) = ![]() треба:
треба:
1) зобразити числа а1, а2,..., аn на числовій прямій (ці числа розташовані в порядку зростання і поділяють числову пряму на декілька проміжків, на яких функція f(х) зберігає свій знак, тобто якщо аt і ak — сусідні точки, то для х є (at : ak функція зберігає знак);
2) визначити знаки функції f (х) на кожному з проміжків;
3) записати відповідь, ураховуючи знак нерівності, даної в умові.
Приклад 4. Розв’яжіть нерівність ![]() < 0.
< 0.
Розв'язання
Позначимо на числовій прямій точки: х = - 4, х = - 2, х = 1, х = 3 та знайдемо знак функції f(x) = ![]() на кожному проміжку (рис. 3).
на кожному проміжку (рис. 3). ![]() Рис. 3
Рис. 3
Відповідь: (-4;-2)![]() (1; 3).
(1; 3).
Метод інтервалів (узагальнений)
Використовується для розв’язування нерівностей f(х) > 0 (f(х) < 0, f(x) ≥ 0, f(x) ≤ 0). Метод ґрунтується на тому, що неперервна на проміжку функція може змінювати знак тільки в тих точках, де її значення дорівнює нулю (але може й не змінювати) (рис. 4).
Щоб розв’язати нерівність методом інтервалів, потрібно:
1) знайти область визначення функції у = f (х);
2) знайти значення х, при яких функція дорівнює нулю (знайти нулі функції): f(х) = 0;
3) розбити область визначення на проміжки, у яких кожний із кінців є коренем рівняння f(х) = 0 або кінцевою точкою проміжку визначення функції у = f(х);
4) визначити знак f(х) на кожному з утворених проміжків;
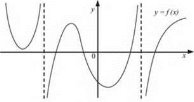 5) об'єднати проміжки, на яких функція f (х) задовольняє нерівність, у множину розв’язків.
5) об'єднати проміжки, на яких функція f (х) задовольняє нерівність, у множину розв’язків.
Рис. 4
Приклад 5. Розв’яжіть нерівність ![]() ≥ 0.
≥ 0.
Розв'язання: Розкладемо чисельник і знаменник дробу на множники й одержимо ![]() ≥ 0. Позначимо на числовій прямій точки 3; -1; 1; - 4, у яких чисельник або знаменник дробу перетворюється на нуль. Ці точки поділяють числову пряму на п’ять проміжків (рис. 5). При х > 3 усі множники чисельника і знаменника дробу додатні, тому дріб є додатним.
≥ 0. Позначимо на числовій прямій точки 3; -1; 1; - 4, у яких чисельник або знаменник дробу перетворюється на нуль. Ці точки поділяють числову пряму на п’ять проміжків (рис. 5). При х > 3 усі множники чисельника і знаменника дробу додатні, тому дріб є додатним.
![]() Рис. 5
Рис. 5
При переході від одного проміжку до іншого дріб змінює знак, тому можна розставити знаки, як показано на рис. 5. Значення х = -1, х = 3 задовольняють дану нерівність, а прих = 1, х = -4 дріб не має змісту. Таким чином, дана нерівність має розв’язок (-∞; - 4)![]() [-1; 1)
[-1; 1)![]() [3; +∞).
[3; +∞).
Відповідь: (-∞; - 4)![]() [-1; 1 )
[-1; 1 )![]() [3; +∞).
[3; +∞).
Тема 16. Числові послідовності. Арифметична і геометрична прогресії
Арифметична прогресія
Арифметичною прогресією називають послідовність а1, а2, а3, .... аn,.... кожний член якої, починаючи з другого, дорівнює попередньому, до якого додається одне й те саме число d яке називають різницею арифметичної прогресії. аn+1 = аn + d, n ∈ N.
Наприклад: 1, 2, 3, 4, 5, 6, ..., n,... — арифметична прогресія, у якій a1 = 1, d = 1;
2, 4, 6, 2n,... — арифметична прогресія, у якій а1 = 2, d = 2.
Визначається n-й член арифметичної прогресії за формулою аn = а1 + d (n - 1),
де n — номер члена, аn — n-й член, а1 — перший член, d — різниця прогресії.
Кожний член арифметичної прогресії, починаючи з другого, дорівнює середньому арифметичному двох сусідніх членів:
an = ![]() .
.
Якщо всі члени деякої числової послідовності, починаючи з другого, задовольняють умові an = ![]() , то ця послідовність є арифметичною прогресією.
, то ця послідовність є арифметичною прогресією.
Сума перших n членів арифметичної прогресії порівнює середньому арифметичному першого і n-го членів цієї прогресії, помноженому на їх кількість:
n = а1 +а2 +...+аn = ![]() ∙ n.
∙ n.
Суму перших n членів арифметичної прогресії можна знайти і за формулою
Sn = ![]() ∙ n.
∙ n.
Геометрична прогресія
Геометричною прогресією називають послідовність b1, b2, b3, ...,bn ... кожний член якої, починаючи з другого, дорівнює попередньому, помноженому на одне і те саме число q(q ≠ 0, |q| ≠ 1), яке називають знаменником геометричної прогресії: bn+1 = bn ∙ q, де q ≠ 0, |q| ≠ 1, n ∈ N. Наприклад: 1, 3, 9, ..., 3n-1,... —геометрична прогресія, у якій b1 = 1, q = 3;
3, 1, ![]() ,
, ![]() ,
, ![]() , ..., 32-n,... — геометрична прогресія, у якій b1 = 3, q =
, ..., 32-n,... — геометрична прогресія, у якій b1 = 3, q = ![]() .
.
Визначається n-й член геометричної прогресії за формулою bn = b1 ∙ qn-1, де n — номер члена, bn — n-й член, b1 — перший член, q — знаменник прогресії.
Модуль кожного члена геометричної прогресії, починаючи з другого, є середнім геометричним двох сусідніх членів: |bn| = ![]() .
.
Якщо всі члени числової послідовності, починаючи з другого, задовольняють умові |bn| = ![]() , то ця послідовність є геометричною прогресією.
, то ця послідовність є геометричною прогресією.
Суму n перших членів геометричної прогресії можна знайти за формулою Sn = b1+ b2 +... + bn = b1 ∙ ![]() .
.
Нескінченно спадна геометрична прогресія
Нескінченно спадна геометрична прогресія — це нескінченна геометрична прогресія, знаменник q якої за модулем є меншим за 1, тобто |q| < 1.
Сумою всіх членів нескінченної спадної геометричної прогресії
S = b1 + b2 + b3 +... + bn + ...
Ця сума визначається за формулою S = ![]() .
.
Приклад. Обчисліть суму.
1 + ![]() +
+![]() +
+ ![]() +
+![]() + … =
+ … = ![]() = 2
= 2
Відповідь: 2.
Тема 1. Початкові поняття планіметрії. Геометрична фігура. Поняття про аксіоми і теореми, поняття про обернену теорему.
Початкові поняття
Геометрія — це наука, яка вивчає властивості геометричних фігур. Прикладами геометричних фігур є трикутник, квадрат, коло (рис. 1). Pозділ геометрії, в якому вивчаються властивості фігур на площині, називається планіметрією.
Точка і пряма є основними геометричними фігурами на площині.
Точка не мас розмірів. Уявлення про точку дає слід кінчика олівця на папері. Точки позначаються великими латинськими літерами А, В,С, D,... (рис. 2).
Уявлення про пряму дає натягнута нитка. Пряма нескінченна. Прямі позначають або однією латинською літерою: а, b, с, ... , або двома великими латинськими літерами, які лежать на прямій: А В, ВС,... (рис. 3).
Частина прямої, обмежена двома точками, називається відрізком. Точки, які обмежують відрізок, називають його кінцями. На рис. 4 зображено відрізок із кінцями в точках А і В. Такий відрізок позначають АВ або ВА.


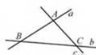
Рис. 1 Рис. 2 Рис. 3
![]()
![]() Рис. 6
Рис. 6
Рис. 4 Рис. 5 ![]()
Променем, або півпрямою, називається частина прямої, обмежена з однієї сторони точкою. На рис. 5 точка О обмежує пряму. Точка О називається початком променя. Промінь позначають або однією латинською літерою (промінь l), або двома великими латинськими літерами, перша із яких позначає початок променя, а друга— довільну точку на промені (промінь ОА, рис. 5). Точка О, яка лежить на прямій, поділяє її на два промені, напрями яких протилежні. Ці промені називають доповнювальними (рис. 6).
Геометрична фігура
Геометричною фігурою називається будь-яке утворення з точок. Геометричні фігури називаються рівними, якщо вони збігаються при накладанні. На рис. 7 зображено рівні відрізки АВ і CD. Це записується так: АВ = CD.
![]() Рис. 7
Рис. 7
Поняття про аксіоми і теореми
Геометрія вивчає властивості фігур, які виражаються різними твердженнями: означеннями, аксіомами, теоремами.
Означення — це твердження, яке пояснює дане поняття через уже відомі поняття.
Аксіома — це твердження, яке приймається на віру (без доведення). Наприклад:
-
Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй (рис. 8).
 Рис. 8
Рис. 8
 Рис. 9
Рис. 9 ![]() Рис. 10
Рис. 10
2. Через будь-які дві точки можна провести пряму, і тільки одну (рис. 9).
3. Пряма розбиває площину на дві півплощини (рис. 10).
4. Із трьох точок прямої одна і тільки одна лежить між двома іншими (рис. 11). ![]() Рис. 11
Рис. 11
Теоремою називається твердження про властивість фігури, істинність якого встановлюється у результаті міркувань. Ці міркування називаються доведенням.
Наведемо приклад. Теорема. Дві різні прямі можуть перетинатися тільки в одній точці.
Доведення: Якби дві різні прямі мали дві точки перетину, то через ці точки проходили б дві різні прямі. А це неможливо, оскільки через дві різні точки можна провести тільки одну пряму (аксіома 2). Отже, дві різні прямі не можуть мага дві різні точки перетину.
Поняття про обернену теорему
Будь-яка теорема складається із двох частин: перша частина — умова (тобто те, що задано), друга частина — висновок (тобто те, що треба довести).
Приклад. Якщо дві різні прямі перетинаються (умова), то вони мають лише одну спільну точку (висновок).
Якщо поміняти місцями висновок і умову В теоремі, то одержимо теорему, обернену АО даної. Дану теорему називають прямою.
Наприклад: теорема «Якщо дві різні прямі мають спільну точку (умова), то вони перетинаються (висновок)» є оберненою до теореми «Якщо дві різні прямі перетинаються (умова), то вони мають лише одну спільну точку (висновок)».
Слід зазначити, що з істинності прямої теореми не завжди випливає справедливість (істинність) оберненого твердження.
Довжина відрізка та її властивості. Відстань між точками
Довжина відрізка та її властивості
Основні властивості вимірювання відрізків виражаються аксіомами.
Аксіома вимірювання відрізків
Кожний відрізок має певну довжину, більшу за нуль. Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою, тобто якщо С — точка відрізка АВ (рис. 12), то АВ = АС + СВ.
![]() Рис. 12
Рис. 12
Знаходження довжини відрізка засноване на порівнянні його з деяким відрізком, який приймається за одиницю вимірювання. Вибравши одиницю вимірювання, можна знайти довжину будь-якого відрізка. На практиці для вимірювання довжин відрізків частіше за все використовують міліметр, сантиметр, дециметр, метр, кілометр. Ці одиниці вимірювання довжин пов’язані між собою, зокрема, 1 км = 1000 м, 1 м = 100 см, 1 дм = 10 см, 1 см = 10 мм.
Рівні відрізки мають однакову довжину і навпаки: якщо відрізки мають однакову довжину, то вони рівні.
Серединою відрізка називається точка цього відрізка, яка ділить його навпіл (тобто на два рівних відрізки).
На рис. 13 точка С — середина відрізка АВ, оскільки АС = СВ (рівні відрізки на рисунках позначають однаковою кількістю рисок).
Основна властивість відкладання відрізків виражається аксіомою.
![]() Рис. 13
Рис. 13
Аксіома відкладання відрізків
На будь-якій півпрямій від її початкової точки можна відкласти відрізок заданої довжини, причому тільки один.
Відстань між точками
Відстанню між точками А і В називається довжина відрізка АВ.
Відстань між точками має такі властивості.
1. Відстань між різними точками є величиною додатною.
2. Відстань від точки А до точки В дорівнює відстані від точки В до точки А, для будь-яких різних точок А і В виконується рівність: АВ = ВА.
3. Для будь-яких точок А, В, С відстань між двома точками менша або дорівнює сумі двох інших відстаней:
 АВ ≤ АС + СВ ( рис. 14,15).
АВ ≤ АС + СВ ( рис. 14,15).
![]()
Рис. 14 Рис. 15
Тема 2. Кути та їх види. Величина кута та їх властивості. Суміжні і вертикальні кути.
Кут
Кутом називається фігура, яка складається з точки, вершини кута, і двох променів, що виходять із цієї точки (промені називаються сторонами кута). Кут позначається знаком ∠. На рис. 1 зображено кут із вершиною О і сторонами ОА і О В. Цей кут позначається так: ∠AOB (літера, яка позначає вершину, завжди ставиться всередині) або ∠O. Нерідко кут позначається цифрою: ∠1. Кут називається розгорнутим, якщо кожна його сторона є продовженням іншої сторони (рис. 2). Два кути називаються рівними, якщо їх можна сумістити накладанням. Наприклад: на рис. 3 ∠1 = ∠2.
![]()
![]()
Рис. 1
Рис. 2
![]()
Рис. 3
Величина кут а та її властивості
Основні властивості вимірювання кутів виражаються аксіомами.
Аксіома вимірювання кутів
Кожний кут має певну градусну міру, більшу за нуль. Розгорнутий кут дорівнює 180°. Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами, тобто якщо промінь ОС проходить між сторонами кута АОВ то ∠AOB = ∠AOC + ∠COB (рис. 4).
За одиницю вимірювання кутів приймається градус (позначається — 1°) — кут, який дорівнює ![]() частині розгорнутого кута. Меншими одиницями вимірювання кутів є мінута (позначається знаком ') і секунда (позначається знаком "): 1° = 60', 1' = 60".
частині розгорнутого кута. Меншими одиницями вимірювання кутів є мінута (позначається знаком ') і секунда (позначається знаком "): 1° = 60', 1' = 60".
Додатне число, яке показує скільки разів градус і його частини вкладуються в даному куті, називається градусною мірою кута.
Рівні кути мають рівні градусні міри і навпаки: якщо кути мають рівні градусні міри, то кути рівні. Кут називається прямим, якщо він дорівнює 90° (рис. 5); гостріш, якщо він менше 90° (рис. 6); тупим, якщо він більше 90°, але менше 180° (рис. 7).
Рис. 4
 Рис. 5
Рис. 5
Рис. 6
Рис. 7
Рис. 8
Бісектрисою кута називається промінь, який виходиш із вершини кута і поділяє його на два рівних кути. На рис. 8 промінь ОС — бісектриса кута АОВ, оскільки ∠AOC = ∠СОВ (рівні кути на рисунках позначають однаковими дужками).
Основна властивість відкладання кутів виражається аксіомою.
Аксіома відкладання кутів
Від будь-якої півпрямої в задану півплощину можна відкласти кут із даною градусного мірою, меншою за 180°, причому тільки один.
Суміжні і вертикальні кути та їх властивості
Оточення. Суміжними називаються два кута, у яких одна сторона спільна, а дві інші є продовженням одна одної.
На рис. 9 кута АОВ і ВОС — суміжні.
Суміжні кута мають таку властивість.
Теореми. Сума суміжних кутів дорівнює 180°.
∠AOB + ∠BOC = 180° (рис. 9), оскільки ∠AOB і ∠BОC — суміжні.
Оточення. Вертикальними називаються два кута, у яких сторони одного кута є продовженням сторін другого.
На рис. 10 вертикальними кутами будуть ∠AOB і ∠COD; ∠AOC і ∠BOD.
Вертикальні кути мають таку властивість. Теореми. Вертикальні кута рівні.∠AOB = ∠COD, ∠AOC = ∠BOD (рис.10), оскільки ∠AOB і ∠COD; ∠AOC і ∠BOD— вертикальні.
Рис. 9 Рис. 10
Тема 3. Паралельні прямі і прямі, що перетинаться.
Дві прямі на площині можуть мати спільну точку або не мата спільних точок.
Дві прямі, які мають спільну ТОЧКУ, називаються прямими, що перетинаються.
Означення. Дві прямі, які лежать в одній площині і не перетинаються, називаються паралельними (рис. 1).
Паралельність прямих позначається знаком ||. Паралельність прямих а і b (рис. 1) записується так: а || b. ![]() Рис. 1
Рис. 1
Аксіома паралельних прямих
Через точку, яка не лежить на даній прямій, можна провести в площині єдину пряму, паралельну даній прямій (рис. 2). ![]() Рис. 2
Рис. 2
Нехай прямі а і Ь перетинаються третьою прямою с (рис. 3), яка називається січною. Тоді утворюється вісім кутів, які мають спеціальні назви: кути 3, 4, 5, 6 — внутрішні, кути 1,2, 7, 8 — зовнішні.
Пари кутів 1 і 5, 2 і 6, 3 і 7, 4 і 8 називаються відповідними, пари кутів 3 і 6, 4 і 5 — внутрішніми різносторонніми, пари кутів 1 і 8, 2 і 7 — зовнішніми різносторонніми. Пари кутів 3 і 5, 4 і 6 називаються внутрішніми односторонніми, 1 і 7, 2 і 8 — зовнішніми односторонніми.
Рис. 3 Рис. 4
Якщо дві паралельні прямі а і b перетнуті прямою с (рис. 4), то:
1) внутрішні різносторонні кута рівні, тобто ∠3 = ∠6, ∠4 = ∠5;
2) сума внутрішніх односторонніх кутів дорівнює 180°, тобто ∠3 + ∠5 = 180°, ∠4 + ∠6 = 180°;
3) відповідні кути рівні, тобто ∠1 = ∠5, ∠2 = ∠6, ∠3 = ∠7, ∠4 = ∠8;
4) зовнішні різносторонні кути рівні, тобто ∠1 = ∠8, ∠2 = ∠7;
5) сума зовнішніх односторонніх кутів дорівнює 180°, тобто ∠1 + ∠7 = 180°, ∠2 + ∠8 = 180°.
Ознаки паралельності прямих
Дві прямі, паралельні третій, паралельні між Якщо а || b, а || с, то b || с (рис. 5).
![]() Рис. 5
Рис. 5
Якщо дві прямі а і b перетинаються третьою прямою с, то прямі а і b (див. рис. 4) паралельні, якщо:
1) внутрішні різносторонні кути рівні, тобто ∠3 = ∠6, ∠4 = ∠5;
2) сума внутрішніх односторонніх кутів дорівнює 180°, тобто ∠3 + ∠5 = 180°, ∠4 + ∠6 = 180°;
3) відповідні кути рівні, тобто ∠1 = ∠5, або ∠2 = ∠6, або ∠3 = ∠7, або ∠4 = ∠8;
4) зовнішні різносторонні кути рівні, тобто ∠1 = ∠8 або ∠2 = ∠7;
5) сума зовнішніх односторонніх кутів дорівнює 180°, тобто ∠1 + ∠7 = 180°, ∠2 + ∠8 = 180°.
Перпендикулярні прямі
Означення. Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.
На рис. 6 зображено перпендикулярні прямі а і b (позначення a ⊥ b), оскільки ∠AOB = 90°.
Теорема. Через кожну точку прямої можна провести перпендикулярну їй пряму, причому тільки одну (рис. 7).
Теорема. Через дану точку поза прямою можна провести перпендикулярну даній пряму, причому тільки одну (рис. 8).
Рис. 6
Рис. 7
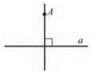
Рис. 8
Теореми про паралельність і перпендикулярність прямих
Теорема. Дві прямі перпендикулярні до третьої прямої, паралельні між собою.
Оскільки а ⊥ с, b ⊥ с, то а ⊥ b (рис. 9).
Теорема. Якщо одна із двох паралельних прямих перпендикулярна до третьої, то і друга пряма перпендикулярна до третьої.
Оскільки а ⊥ b, а ⊥ с, то b ⊥ c (рис. 9). 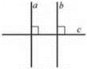 Рис. 9
Рис. 9
Відстань від точки до прямої
Відстанню від точки до прямої називається довжина перпендикуляра, опущеного із даної точки на дану пряму.
На рис. 10 відстанню від точки А до прямої а є довжина перпендикуляра АО.
Відстанню між паралельними прямими називаються відстань від будь-якої точки однієї прямої до другої прямої.
На рис. 11 відстанню між паралельними прямими а і b є довжина відрізка AO (AO ⊥ b).
Відстані від усіх точок прямої до паралельної прямої — рівні.
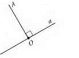
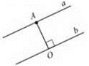
Рис. 10 Рис. 11
Тема 4. Трикутники та їх види. Ознаки рівності трикутників. Рівнобедренний трикутник та його властивості.
Трикутник
Трикутник — це геометрична фігура, що складається із трьох точок, які не лежать на одній прямій, і відрізків, які з’єднують ці точки. Точки називають вершинами трикутника, а відрізки — його сторонами. На рис. 1 зображено трикутник із вершинами А, В, С і сторонами АВ, ВС, АС. Цей трикутник позначається так: ∆АВС.
Кути CAB, ABC, АСВ називаються кутами трикутника. Найчастіше їх позначають однією буквою: ∠A, ∠B, ∠C. Сторону ВС і кут А трикутника ABC називають протилежними. Протилежними є також cтopона АC і кут В, сторона АВ і кут С. Кути А і С, В і С, А і В називаються прилеглими до сторін АС, ВС, АВ.
Периметром трикутника називають суму довжин трьох сторін трикутника. Якщо периметр трикутника позначити буквою Р, а довжини сторін ВС, СА і АВ — відповідно, через а, b, с (рис. 2), то Р = а + b + с.
Рис. 1 Рис. 2
Теорема. У будь-якому трикутнику кожна сторона менша за суму двох інших сторін (нерівність трикутника), тобто c < a + b, a < c + b, b < a + c (рис. 2).
Види трикутників
Залежно від довжин сторін розрізняють різносторонні, рівнобедрені і рівносторонні (або правильні) трикутники.
Трикутник, який має три різні за довжиною сторони, називають різностороннім (рис. 3).  рис. 3
рис. 3  рис. 4
рис. 4
 Трикутник, який має дві рівні сторони, називають рівнобедреним (рис. 4). Рівні сторони називаються бічними, а третя сторона — основою трикутника. На рис. 4 ∆ABC — рівнобедрений, у нього АВ = ВС, тобто АВ, ВС— бічні сторони, АС — основа. Трикутник, у якого всі сторони рівні, називають рівностороннім, або правильні (рис. 5). У рівностороннього трикутника всі кути рівні, величина кожного з них дорівнює 60°. Рис. 5
Трикутник, який має дві рівні сторони, називають рівнобедреним (рис. 4). Рівні сторони називаються бічними, а третя сторона — основою трикутника. На рис. 4 ∆ABC — рівнобедрений, у нього АВ = ВС, тобто АВ, ВС— бічні сторони, АС — основа. Трикутник, у якого всі сторони рівні, називають рівностороннім, або правильні (рис. 5). У рівностороннього трикутника всі кути рівні, величина кожного з них дорівнює 60°. Рис. 5
 Залежно від величини кутів розрізняють гострокутні, прямокутні й тупокутні трикутники.
Залежно від величини кутів розрізняють гострокутні, прямокутні й тупокутні трикутники.
 Гострокутним називається трикутник, у якого всі кути гострі (рис. 6).
Гострокутним називається трикутник, у якого всі кути гострі (рис. 6).
 Прямокутним називається трикутник, у якого є прямий кут (рис. 7). Сторону прямокутного трикутника, протилежну прямому куту, називають гіпотенузою, а дві інші сторони — катетами. На рис. 7 сторона АС — гіпотенуза, сторони АВ і ВС— катети.
Прямокутним називається трикутник, у якого є прямий кут (рис. 7). Сторону прямокутного трикутника, протилежну прямому куту, називають гіпотенузою, а дві інші сторони — катетами. На рис. 7 сторона АС — гіпотенуза, сторони АВ і ВС— катети.
Тупокутним називаєтеся трикутник, у якого є тупий кут (рис. 8).
Висоти, бісектриси і медіани трикутника
Висотою трикутника називають перпендикуляр, проведений із його вершини до прямої, яка має протилежну сторону. На рис. 9 відрізок BD — висота відповідно гострокутного (рис. 9, а), тупокутного (рис. 9, б) і прямокутного (рис. 9, в) трикутників.
Рис. 9 Рис. 10
 Висоти трикутника (або їх продовження) перетинаються в одній точці (рис. 10).
Висоти трикутника (або їх продовження) перетинаються в одній точці (рис. 10).  Медіаною трикутника називають відрізок, який з’єднує вершину трикутника із серединою протилежної сторони. Нарис. 11 ВМ — медіана трикутника АВС.
Медіаною трикутника називають відрізок, який з’єднує вершину трикутника із серединою протилежної сторони. Нарис. 11 ВМ — медіана трикутника АВС.
Медіани трикутника перетинаються в одній точці (рис. 12), яка називаєтеся центрам мас трикутника.
Бісектрисою трикутника називають відрізок, який з’єднує вершину кута і точку протилежної сторони й ділите кут навпіл. На рис. 13 BL — бісектриса трикутника ABC.
 Усі бісектриси трикутника перетинаються в одній точці (рис. 14). яка є центром кола вписаного в трикутник.
Усі бісектриси трикутника перетинаються в одній точці (рис. 14). яка є центром кола вписаного в трикутник.
Середня лінія трикутника.
Середньою лінією трикутника називають відрізок, який з’єднує середини двох його сторін. На рис. 15 MN— середня лінія
Середня лінія трикутника паралельна третій стороні і дорівнює її половині.
На рис. 15 MN ⊥ АС, MN = ![]() АС.
АС.
Поняття про рівність фігур
 Перетворення однієї фігури в іншу називається рухом, якщо воно зберігає відстані між точками, тобто будь-які дві точки А і В однієї фігури F переводяться в точки А1 і В1 другої фігури F1 так, що AВ = A1В1 (рис. 16).
Перетворення однієї фігури в іншу називається рухом, якщо воно зберігає відстані між точками, тобто будь-які дві точки А і В однієї фігури F переводяться в точки А1 і В1 другої фігури F1 так, що AВ = A1В1 (рис. 16).
Дві фігури F1 і F2 називаються рівними, якщо вони рухом переводяться одна в одну. Запис F = F1 означає, що фігура F дорівнює фігурі F1.
Перетворення симетрії відносно точки і відносно прямої та поворот площини навколо точки є рухами.
На рис. 17 зображено рівні трикутники ABC і А1B1С1. Рівність трикутників позначається так: ∆АВС = ∆А1В1С1.
Якщо два трикутники рівні, то елементи (тобто сторони, кути, медіани, бісектриси, висоти тощо) одного з них відповідно дорівнюють елементам другого. На рис. 24 ∠A = ∠A1, ∠B = ∠B1, ∠C = ∠C1, AB = A1B1, BC = B1C1, AC = A1C1.
На рисунку рівні відрізки позначаються рівною кількістю рисок, а рівні кути — однаковою кількістю дужок. У рівних трикутників проти рівних сторін лежать рівні куга, а проти рівних кутів — рівні сторони.
Перша ознака рівності трикутників (за двома сторонами і кутом між ними)
Якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники є рівними (рис. 18).
Друга ознака рівності трикутників (за стороною і двома прилеглими кутами)
Якщо сторона і два прилеглі до неї кути одного трикутника відповідно дорівнюють стороні і двом прилеглим до неї кутам другого трикутника, то такі трикутники — рівні (рис. 19).
Третя ознака рівності трикутників (за трьома сторонами)
Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам другого трикутника, то такі трикутники є рівними (рис. 20).
 Рис. 17
Рис. 17
 Рис. 18
Рис. 18
Рис. 19
Рис. 20
Два прямокутні трикутники рівні, якщо виконується одна з умов:
1) два катети одного трикутника відповідно дорівнюють двом катетам другого трикутника;
2) катет і гострий кут одного трикутника відповідно дорівнюють катету і гострому кугу друг ого трикутника;
3) гіпотенуза і гострий кут одного трикутника дорівнюють гіпотенузі і гострому куту другого трикутника;
4) гіпотенуза і катет одного трикутника відповідно дорівнюють гіпотенузі і катету другого трикутника.
 Властивості рівнобедреного трикутника
Властивості рівнобедреного трикутника
Рівнобедрений трикутник має такі властивості. Рис.21.
1. У рівнобедреного трикутника кути при основі рівні. На рис. 21 АВ = ВС, тобто ∆АВС — рівнобедрений, отже, ∠A = ∠C.
2. У рівнобедреного трикутника медіана, проведена до основи, є і бісектрисою, і висотою.
 3. У рівнобедреного трикутника висота, проведена до основи, є і бісектрисою, і медіаною. Рис. 22
3. У рівнобедреного трикутника висота, проведена до основи, є і бісектрисою, і медіаною. Рис. 22
4. У рівнобедреного трикутника бісектриса, проведена до основи, є і висотою, і медіаною. а рис. 22 у ∆ABC (АВ = ВС) відрізок BD є і медіаною (AD = DC), і висотою (BD ⊥ АС), і бісектрисою (∠ABD = ∠CBD).
Ознаки рівнобедреного трикутника
Якщо в трикутнику:
1) два кути рівні,
2) медіана і висота збігаються,
3) медіана і бісектриса збігаються,
4) висота і бісектриса збігаються, то він є рівнобедреним.
Тема 5. Сума кутів трикутника
Сума кутів трикутника
 Теореми про суму кутів трикутники. Сума кутів трикутника дорівнює 180°. На рис. 1 ∠А + ∠В + ∠C = а + β + γ= 180°.
Теореми про суму кутів трикутники. Сума кутів трикутника дорівнює 180°. На рис. 1 ∠А + ∠В + ∠C = а + β + γ= 180°.
Зовнішнім кутом трикутника називається кут, суміжний із кутом трикутника при цій вершині. На рис. 2 ∠BAD — зовнішній кут трикутника ABC. Рис. 1
Із теореми про суму кутів трикутника випливають такі висновки:
1. У будь-якого трикутника хоча б два кути є гострими.
2. Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних із ним.
На рис. 2 ∠DAВ - ∠ABC + ∠BCA.
Рис. 2 Рис. З
3. Зовнішній кут трикутника більший за будь-який внутрішній кут, не суміжний із ним. На рис. 2 ∠DAB > ∠B, ∠DAB > ∠C.
4. Сума гострих кутів прямокутного трикутника дорівнює 90°.
На рис. 3 ∠B + ∠C = 90°.
Тема 6. Подібність трикутників. Теорема Піфагора.
Поняття про подібність фігур
Фігура F1 називається подібною до фігури F(F1 ~ F). якщо існує відображення фігури F на фігуру F1, при якому для будь-яких двох точок А і B фігури F тa їх образів A1 і В1фігури F1, відношення відстаней АВ і А1В1 є величиною сталою (рис. 1).
Число k = ![]() називають коефіцієнтом подібності.
називають коефіцієнтом подібності.
У подібних фігур відповідні кути рівні, а відповідні відрізки пропорційні. Зокрема, у подібних трикутниках ABC і А1В1С1 (рис. 2):
∠A = A1, ∠B = ∠B1, ∠C = ∠C1;
Рис. 1
Рис. 2
![]() =
= ![]() =
= ![]() .
.
Ознаки подібності трикутників
Перша ознака подібності трикутників (за двома кутами)
Якщо два кути одного трикутника відповідно дорівнюють двом кутам другого трикутника, то такі трикутники є подібними (рис. 3).
Друга ознака подібності трикутників (за двома сторонами і кутом між нами)
Якщо дві сторони одного трикутника пропорційні двом сторонам другого трикутника і кути, утворені цими сторонами, рівні, то такі трикутники є подібними(рис.4)
![]() =
= ![]()
Рис. 3
Рис. 4
Третя ознака подібності трикутників (за трьома сторонами) Якщо три сторони одного трикутника пропорційні трьом сторонам другого трикутника, то такі трикутники є подібними (рис. 5). ![]() =
= ![]() =
= ![]()
 Рис. 5
Рис. 5
Теорема Піфагора та її наслідки
Теореми. У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів його катетів. На рис. 6 АВ2 = АС2 + ВС2, або с2 = а2 + b2.
Наслідки з теореми Піфагора
1. У прямокутному трикутнику будь-який із катетів менший за гіпотенузу.
2. Квадрат катета дорівнює різниці квадратів гіпотенузи і другого катета.
а2 = с2 - b2, b2 = с2 - а2.
![]()
Рис. 6
3. Площа квадрата, побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі площ квадратів, побудованих на катетах. На рис.7
S = S1 + S2.
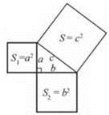 Теореми, обернена до теореми Піфагора
Теореми, обернена до теореми Піфагора
Якщо квадрат однієї сторони трикутника дорівнює сумі квадратів двох інших сторін, то цей трикутник є прямокутним.
Рис. 7
Тема 7. Поняття площі. Площа трикутника.
 Поняття про площі. Основні властивості площ
Поняття про площі. Основні властивості площ
Геометричну фігуру називають простою, якщо її можна розбити на скінченне число плоских трикутників (плоским трикутником називається скінченна частина площини, обмежена трикутником) (рис. 1). Рис. 1
Площа простої фігури — це додатна величина, числове значения якої має такі властивості:
1) рівні фігури мають рівні площі;
2) якщо фігура розбивається на частини, кожна з яких є простою фігурою, то площа всієї фігури дорівнює сумі площ її частин;
3) площа квадрата зі стороною, яка дорівнює одиниці вимірювання, дорівнює одиниці.
Площа квадрата зі стороною 1 мм, 1 см, 1 дм, 1м відповідно дорівнює 1 мм2, 1 см2, 1 дм2, 1 м2.
 Якщо фігура не є простою, її площу визначають таким чином. Дана фігура має площу S, якщо існують прості фігури, які обмежують її та містяться в ній із площами, що як завгодно мало відрізняються від площі S (рис. 2). Рис. 2
Якщо фігура не є простою, її площу визначають таким чином. Дана фігура має площу S, якщо існують прості фігури, які обмежують її та містяться в ній із площами, що як завгодно мало відрізняються від площі S (рис. 2). Рис. 2
Площа трикутника
 Площа трикутника дорівнює півдобутку його сторони (основи) на проведену до неї висоту (рис. 3):
Площа трикутника дорівнює півдобутку його сторони (основи) на проведену до неї висоту (рис. 3):
5 = ![]() ah. Рис. 3
ah. Рис. 3
 Крім того, площу трикутника можна обчислити за формулами. Наприклад, за формулою Герона: S =
Крім того, площу трикутника можна обчислити за формулами. Наприклад, за формулою Герона: S = ![]() ,
,
де а, b,с — сторони трикутника, р = ![]() — його півпериметр.
— його півпериметр.
Рис. 4
Площа прямокутного трикутника дорівнює половині добутку його катетів (рис. 4): S = ![]() аb.
аb.
Площу правильного (рівностороннього) трикутника можна обчислити за формулою: S = ![]() . де а — його сторона.
. де а — його сторона.
Площі подібних трикутників відносяться як квадрати відповідних лінійних елементів.
Тема 8. Коло і круг. Дотична до кола
Коло і круг
Геометричним місцем точок називають фігуру, що складається з усіх точок площини, які мають певну властивість.
Колам називають геометричне місце точок площини, рівновіддалених від даної точки, яка називається центрам кола (рис. 1).

Рис. 1
Відстань від точки кола до його центра називається радіусам.
Радіусом називають також будь-який відрізок, що з’єднує точку кола з його центром. На рис. 2 ОА, ОВ, ОС — радіуси кола
Рис. 2
Відрізок, який з’єднує дві точки кола, називається хордою.
Хорда що проходить через центр кола, називається діаметром кола.
На рис. 2 DF, ВС — хорди, ВС — діаметр.
Рівні хорди кола рівновіддалені від центра. Дві хорди кола які рівновіддалені від центра, мають однакову довжину.
Якщо АВ = CD (рис. 3), то ON = ОМ, і навпаки, якщо ОМ = ON, то АВ = CD. Діаметр кола, який проходить через середину хорда, відмінної від діаметра, перпендикулярний до неї.
 Рис. 3
Рис. 3
Діаметр кола, перпендикулярний до хорди, проходить через її середину.
Якщо AM = МВ (рис.4), то CD ⊥ АВ. і навпаки, якщо CD ⊥ АВ, то AM = MB.
Круг — це геометричне місце точок площини, відстань яких від даної точки, що називається центром, не перевищує даної відстані, яка називається радіусом (інакше кажучи, кругом називається скінченна частина площини, обмежена колом).
На рис. 5 О — центр круга, ОА — радіус крута.
 Рис. 4
Рис. 4
 Рис. 5
Рис. 5
Дотична до кола та її властивості
Пряму, що проходить через точку кола перпендикулярно до радіуса, проведеного до даної точки, називають дотичною до кола. При цьому дану точку кола називають точкою дотику.
Дотична до кола має з колом тільки одну спільну точку — точку дотику.
Нарис. 6 пряма АВ — дотична до кола, бо АВ ⊥ ОМ. М—точка дотику.
Дотичними колами називають два кола які мають лише одну спільну точку (у цій точці вони мають спільну дотичну). Дотик кіл називається внутрішнім дотиком, якщо центри кіл лежать по один бік від їх спільної дотичної (рис. 7).
Дотик кіл називається зовнішнім дотиком, якщо центри кіл лежать по різні боки від їх спільної дотичної (рис. 8).
Рис. 6. Рис. 7 Рис8.
Тема 9. Вписані кути.
Вимірювання вписаних кутів
Центральним кутам у колі називають кут із вершиною в його центрі, зі сторонами, утвореними двома радіусами.
На рис. 1 ∠AOB — центральний кут. Частину кола, розташовану всередині центрального кута, називають дугою кола, яка відповідає даному центральному куту.
На рис. 1 виділена дуга АВ (позначення: ОАВ) відповідає центральному куту АОВ. Також кажуть, що кут АОВ опирається на дугу АВ.
Градусною мірою дуги кола називається градусна міра відповідного центрального кута. На рис. 1 ∠AOB = ОАВ.
Вписаним кутам називають кут, вершина якого лежить на колі, а сторони перетинають його.
На рис. 2 ∠ABC — вписаний.
Дуга кола, яка лежить усередині вписаного кута, називається дугою, яка відповідає даному вписаному куту.
На рис. 2 виділена дуг а АС відповідає вписаному куту ABC (кажуть також, що кут АВС опирається на дугу АС).
 Рис. 1
Рис. 1
 Рис. 2
Рис. 2
Теорема. Вписаний кут вимірюється половиною дуги, на яку він опирається (дорівнює половині центрального кута, який опирається на цю ж дугу).
На рис. 3 ∠AВС = ![]() OAС =
OAС = ![]() ∠AОС. Із цієї теореми випливає, що:
∠AОС. Із цієї теореми випливає, що:
1. Вписані кути, які опираються на одну й ту ж дугу, рівні. На рис. 4 ∠AВ1С = ∠AВ2С = ∠AВ3С.
2. Вписаний кут, який опирається на діаметр, є прямим. На рис. 5 ∠ACB = 90°.
 Рис. З
Рис. З
 Рис. 4
Рис. 4
 Рис.5
Рис.5
Тема 10. Довжина кола і площа круга.
Довжина кола Довжина С кола обчислюється за формулою: С = 2![]() R або С =
R або С = ![]() d.
d.
де R — радіус кола, d — його діаметр (рис. 1).
Відношення довжин двох кіл дорівнює відношенню їх радіусів: ![]() =
= ![]() .
. Рис. 1
Рис. 1
Довжина дуги
Довжина дуги кола радіуса R може бути обчислена за формулою:
l = ![]() (рис. 2),
(рис. 2),
де l — довжина дуги; n° — градусна міра дуги.  Рис. 2
Рис. 2
Число ![]()
Відношення довжини кола до його діаметра не залежить від кола, тобто воно одне й те ж для будь-яких кіл (рис. 3).
Це відношення прийнято позначати буквою ![]() :
:
![]() =
= ![]() =
= ![]() :
: ![]() = 3,1415926...
= 3,1415926...  Рис. 3
Рис. 3
Площа круга і його частин
Площа круга обчислюється за формулами:
S = ![]() R2 або S =
R2 або S = ![]() ,
,
де R — радіус круга, d — його діаметр (рис. 4).
Круговим сектором називається частина круга, яка лежить усередині відповідного центрального кута (рис. 5).
Площа сектора може бути обчислена за формулою
S = ![]() (рис. 5),
(рис. 5),
де n° — градусна міра дуги сектора.
 Рис. 4
Рис. 4 Рис. 5
Рис. 5
Круговим сегментом називається спільна частина круга і півплощини (рис. 6). Якщо круг перетнути прямою, він ділиться на два кругових сегменти.
Площу кругового сегмента можна обчислити за формулою:
Sкруг сегмента = Sкруг сектора + S∆АОВ (рис. 6), причому при а < 180° беремо знак «-», а при а > 180° — знак «+». Рис. 6
Рис. 6
Площа кругового сегмента
Круговим кільцем називається частина площини, обмежена двома концентричними колами.
Площа кругового кільця дорівнює різниці площ зовнішнього і внутрішнього кругів.
S = ![]() (D2 - d2),
(D2 - d2),
де D — діаметр зовнішнього круга, d — діаметр внутрішнього круга (рис. 7). ![]() Рис. 7
Рис. 7
Тема 11. Вписані та описані трикутники.
Властивості серединного перпендикуляра до відрізка Геометричним місцем точок площини, рівновіддалених від двох даних точок, є серединний перпендикуляр до відрізка, що з’єднує ці дві точки (серединний перпендикуляр — це пряма, що проходить через середину відрізка перпендикулярно до нього) (рис. 1).
Якщо АС= СВ і l — серединний перпендикуляр до відрізка AB, то С належить l, і навпаки, якщо С належить серединному перпендикуляру l, то СА = СВ.
 Рис. 1
Рис. 1
Коло, описане навколо трикутника
Коло називають описаним навколо трикутника, якщо воно проходить через усі його вершини (рис. 2). Трикутник при цьому має назву вписаного.
Центр кола, описаного навколо трикутника, є точкою перетину серединних перпендикулярів до сторін трикутника (рис. 3).
Навколо будь-якого трикутника можна описати коло, причому тільки одне. Радіус R описаного кола можна обчислити за формулами:R = ![]() або R =
або R = ![]() ,
,
 Рис. 2
Рис. 2 Рис. 3
Рис. 3
де а, b, с — довжини сторін трикутника, р = ![]() — півпериметр трикутника, S — його площа.
— півпериметр трикутника, S — його площа.
Радіус R кола, описаного навколо рівносторонього трикутника, можна обчислити за формулою:
R = ![]() =
= ![]() ,
,
де а — довжина сторони трикутника
Радіус R кола описаного навколо прямокутного трикутника, можна обчислити за формулою:
R = ![]() =
= ![]() ,
,
де а, b — довжини катетів прямокутного трикутника, с — довжина його гіпотенузи.
Рис. 4
Рис. 5
Центр кола, описаного навколо гострокутного трикутника, міститься всередині трикутника (рис. 4); описаного навколо тупокутного трикутника — поза трикутником (рис. 5); описаного навколо прямокутного трикутника — на середині гіпотенузи (рис. 6).  Рис. 6
Рис. 6
Властивості бісектриси кута
Геометричним місцем точок площини, рівновіддалених від сторін даного кута є його бісектриса.
Якщо точка М (рис. 7) рівновіддалена від сторін кута АОВ (МА = MB, МА ⊥ ОА, MB ⊥ ОВ), то точка М лежить на бісектрисі ОС кута АОВ, і навпаки, якщо точка М лежить на бісектрисі ОС кута АОВ, то вона рівновіддалена від його сторін (тобто МА = MB, МА ⊥ ОА, MB ⊥ ОВ).
Рис. 7
Коло, вписане в трикутник
Коло називають вписаним у трикутник, якщо воно дотикається до всіх його сторін (рис. 8). Трикутник при цьому називається описаним навколо кола.
Центр кола, вписаного в трикутник, є точкою перетину його бісектрис (рис. 9). У будь-який трикутник можна вписати коло, причому тільки одне.
Радіус r вписаного в трикутник кола можна обчислити за формулами:
r = ![]() або r =
або r = ![]()
де а, b, с — довжини сторін трикутника, S — його площа, р — півпериметр,
p = ![]() .
. Рис. 8
Рис. 8
Радіус r кола вписаного в рівносторонній трикутник, можна обчислити за формулою:
r = ![]() =
= ![]() =
= ![]() ,
,
де а — довжина сторони трикутника, a R — радіус кола, описаного навколо трикутника.  Рис. 9
Рис. 9
Радіус r кола, вписаного в прямокутний трикутник, можна обчислити за формулою:
r = ![]() .
.
де а, b — довжини катетів прямокутного трикутника, с — довжина його гіпотенузи.
Тема 12. Тригонометричні функції гострого кута прямокутного трикутника
Синус, косинус, тангенс і котангенс гострого куга прямокутною трикутника
Синусом гострого кута а прямокутного трикутника називають відношення катета, протилежного куту а, до гіпотенузи (рис. 1): sin a = ![]() .
.
Косинусом гострого кута а прямокутного трикутника називають відношення катета, прилеглого до кута а, до гіпотенузи (рис. 1):
сos a = ![]() .
. Рис. 1
Рис. 1
Тангенсам гострого кута а прямокутного трикутника називають відношення катета, протилежного куту а, до катета, прилеглого до кута а (рис. 1):
tg a = ![]() .
.
Котангенсом гострого кута а прямокутного трикутника називають відношення катета, прилеглого до кута а, до катета, протилежного куту а (рис. 1): ctga = ![]() .
.
Значення синуса, косинуса, тангенса і котангенса деяких кутів подано в таблиці.
|
Кута\Функція |
0° |
30° |
45° |
60° |
90° |
|
sin a |
0 |
|
|
|
1 |
|
cos a |
1 |
|
|
|
0 |
|
tg a |
0 |
|
1 |
|
не існує |
|
ctg a |
не існує |
|
1 |
|
0 |
З означення sina, cosa, tga, ctga випливають такі правила
1. Невідомий катет дорівнює добутку гіпотенузи на синус кута, протилежного невідомому катету, або на косинус кута, прилеглого до невідомого катета (рис. 2):
а = csina = ccosβ, b= csinβ= ccosa.
 Рис. 2
Рис. 2
2. Невідомий катет дорівнює добутку другого катета на тангенс кута, протилежного невідомому катету, або на котангенс кута, прилеглого до невідомого катета (рис. 2):
а = b ∙ tga = b ∙ ctgβ, b = a ∙ tgβ = a ∙ ctga.
Основні тригонометричні тотожності
sin2a + cos2a = 1, tg a = ![]() , ctga =
, ctga = ![]() ,
,
tga ∙ ctga = 1, 1 + tg2 a = ![]() , 1 + ctg2a =
, 1 + ctg2a = ![]() , де 0° < а < 90°.
, де 0° < а < 90°.
При зростанні гострого кута синус та тангенс кута зростають, а косинус та котангенс — спадають. Дія будь-якого кута а прямокутного трикутника:
sin(90°- a)= cosa, cos(90° - a) = sina, tg(90° - a)= ctga, ctg(90°- a) = tga.
Тема 13. Розв’язування довільних трикутників.
Теореми синусів і косинусів
Теореми косинусів. Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними.
Наприклад: у ∆ABC (рис. 1)а2 = с1 + b2 -2bc cosa, b2 = а2 +с2 -2ас cos β, с2 = а2 + b2 - 2ab cosγ.
Теореми синусів. У довільному трикутнику відношення будь-якої сторони до синуса протилежного кута стале і дорівнює діаметру описаного
навколо нього кола (рис. 2):
![]() =
= ![]() =
= ![]() =2R.
=2R.  Рис. 1
Рис. 1
Варто пам’ятати, що синуси суміжних кутів рівні, а їх косинуси — протилежні числа:
sin(180° - a) = sina, cos(180° - a) = - cosa.  Рис. 2
Рис. 2
Poзв’язyвання трикутників
Розв’язуванням трикутників називається знаходження всіх його шести елементів (тобто трьох сторін і трьох кутів) за будь-якими трьома даними елементами, що визначають трикутник.
Розгляньмо три задачі на розв’язування трикутників. При цьому будемо користуватися такими позначеннями для сторін трикутника ABC: АВ = с, ВС = а, СА = b (див. рисунок 1).
Задача 1. Дано: a, b, ∠С. Знайти: с, ∠А, ∠В (розв'язування трикутника за двома сторонами і кутам між ними).
Розв’язання
За теоремою косинусів знаходимо с:
c = ![]() .
.
Користуючись теоремою косинусів, маємо:
cos ∠A = ![]() , ∠А = arcos =
, ∠А = arcos = ![]() .
.
Далі ∠В = 180° - ∠А - ∠С.
Задачи 2. Дано: а, ∠В, ∠С. Знайти: ∠А, b, с (розв'язування трикутника за стороною і двома прилеглими кутами).
Розв’язання
∠А — 180° - ∠В - ∠С. За теоремою синусів знаходимо b і с:
b = a![]() ; c = a
; c = a![]() .
.
Задача 3. Дано: а, b, с. Знайти: ∠А, ∠В, ∠С (розв'язування трикутника за трьома сторонами).
Розв’язання
Користуючись теоремою КОСИНУСІВ, знаходимо:
cos ∠A = ![]() , звідси ∠А = arcos =
, звідси ∠А = arcos = ![]() .
.
Аналогічно знаходимо АВ. Тоді АС = 180° - ∠А - ∠В.
Тема 15. Трапеції, їх види та властивості. Вписані і описані чотирикутники
Трапецій і а її властивості
Трапецією називаєтеся чотирикутник, у якого дві сторони паралельні, а дві інші сторони не паралельні.
Паралельні сторони трапеції називають основами, а непаралельні сторони — бічними. На рис. 1 чотирикутник ABCD— трапеція, оскільки AD || ВС АВ ∦ СD сторони ВС і AD — основи трапеції, АВ і CD — бічні сторони трапеції.
Висотою трапеції називають перпендикуляр, проведений із будь-якої точки однієї з основ на пряму, що містить другу основу (або відстань між основами трапеції).
 Рис. 1
Рис. 1
На рис. 2 MN — висота трапеції ABCD.
Середньою лінією трапеції називають відрізок, що сполучає середини бічних сторін трапеції.
На рис. 2KL — середня лінія.
Властивості трапеції
1. Сума кутів трапеції, прилеглих до бічної сторони, дорівнює 180°.
На рис. 1 ![]() A + ∠B = ∠C + ∠D = 180°.
A + ∠B = ∠C + ∠D = 180°.
2. Середня лінія трапеції паралельна основам і дорівнює їх півсумі.
Нарис.2KL || AD,KL || ВС, KL = ![]() .
. Рис. 2
Рис. 2
Трапецію, у якої бічні сторони рівні, називають рівнобічною (рівнобедреною) трапецією.
На рис. З зображено рівнобічну трапецію ABCD.
Властивості рівнобічної трапеції У рівнобічнім трапеції (рис. 3):
1. Кута при основі рівні: ∠A = ∠D, ∠B = ∠C.
2. Діагоналі рівні: АС = BD. ![]() Рис. 3
Рис. 3
Прямокутною називають трапецію, у якої одна з бічних сторін перпендикулярна до основ (рис. 4). Ця бічна сторона є висотою трапеції.
Якщо у рівнобічній трапеції діагоналі взаємно перпендикулярні, то її висота дорівнює середній лінії (рис. 5):
BН = . 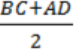
![]() Рис. 4
Рис. 4
 Рис. 5
Рис. 5
Коло можна описати лише навколо рівнобічної трапеції (рис. 6).
Висота рівнобічної трапеції, у яку можна вписати коло, є середнім геометричним між її основами (рис. 7):  Рис. 6
Рис. 6
Якщо у рівнобічну трапецію вписано коло, то її бічна сторона дорівнює середній лінії (рис. 7): AB = CD = ![]() .
. Рис. 7
Рис. 7
Властивості чотирикутників
Вписаного в коло (рис. 8) Описаного навколо кола (рис. 9)
∠A + ∠C = 180° = ∠B + ∠D а + с = b + d
ас + bd = k1k2 — теорема Птолемея
S = p ∙ r, де p = ![]()
Рис. 8
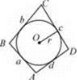
Рис. 9
Тема 16. Площа чотирикутників
Площа паралелограма, прямокутника, ромба, квадрата, трапеції
Площа прямокутника дорівнює добутку двох його суміжних сторін (рис. 1):
S = а ∙ b. ![]() Рис. 1
Рис. 1
Площа прямокутника дорівнює половині квадрата його діагоналі, помноженої на синус кута між діагоналями (рис. 2):
S = ![]() d2sin
d2sin![]() .
.![]() Рис. 2
Рис. 2
Площа квадрата дорівнює квадрату його сторони (рис. 3):
S = а2. ![]() Рис. 3
Рис. 3
Площа квадрата дорівнює половині квадрата його діагоналі (рис. 4):
S = ![]() d2.
d2. ![]() Рис. 4
Рис. 4
Площа паралелограма дорівнює добутку його сторони (основи) на висоту, проведену до неї (рис. 5): S = ah. 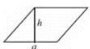 Рис. 5
Рис. 5
Площа паралелограма дорівнює добутку двох його суміжних сторін на синус кута між ними (рис. 6): S = ab sin а. ![]() Рис. 6
Рис. 6
Площа паралелограма дорівнює половині добутку його діагоналей на синус кута між ними (рис. 7): S = ![]() d1d2sin
d1d2sin![]() .
.![]() Рис. 7
Рис. 7
Площа ромба дорівнює добутку квадрата його сторони на синус кута ромба (рис. 8): S = a2 sin а. ![]() Рис. 8
Рис. 8
Площа ромба дорівнює півдобутку його діагоналей (рис. 9): S = ![]() d1d2.
d1d2.
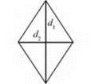 Рис. 9
Рис. 9
Площа трапеції дорівнює добутку півсуми основ на висоту (рис. 10):
S = ![]() ∙ h.
∙ h. 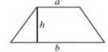 Рис. 10
Рис. 10
Площа трапеції дорівнює добутку середньої лінії на висоту (рис. 11):
S = mh. ![]() Рис. 11
Рис. 11
Якщо діагоналі рівнобічної трапеції взаємно перпендикулярні, то S = h2, де А — висота трапеції (рис. 12).  Рис. 12
Рис. 12
Тема 18. Правильні многокутники та їх властивості
Основні теоретичні відомості
Опуклий многокутник називають правильніш, якщо у нього всі сторони рівні і всі кути рівні (рис. 1).
Кожний внутрішній кут правильного n-кутника дорівнює ![]() , а зовнішній —
, а зовнішній — ![]() .
.
 Рис. 1
Рис. 1
Кожний правильний многокутник можна вписати в деяке коло і описати навколо кола Вписан і й описані кола правильного многокутника мають один і той же центр, який називають центрам правильного многокутника (рис. 2).
Радіуси r і R відповідно вписаного і описаного кіл правильного n-кутника пов’язані між собою співвідношенням r = Rcos![]() .
. Рис. 2
Рис. 2
Співвідношення між стороною an правильного n-кутника та радіусами описаного R і вписаного r кіл виражається формулами:
an = 2Rsin![]() , an = 2rtg
, an = 2rtg![]()
для правильного трикутника:
а3 = R![]() , a3 = 2
, a3 = 2![]() (рис. 4);
(рис. 4);
для правильного чотирикутника (квадрата):
а4 = R![]() , а4 = 2r (рис. 5);
, а4 = 2r (рис. 5);
 для правильного шестикутника:
для правильного шестикутника:
a6 = R, a6 = ![]() (рис 6.). Рис. 6
(рис 6.). Рис. 6
Апофемою правильного многокутника називають перпендикуляр, проведений із центра правильного многокутника до його сторони (рис. 7).
Рис. 3
Рис. 4
Рис. 5
Рис. 7
Тема 19. Декартові координати на площині
Декартові координат. Визначення декартових координат на площині
Декартова система координат на площині задається двома взаємно перпендикулярними осями (вісь ОХ — вісь абсцис, вісь ОУ — вісь ординат), які мають спільний початок О (початок координат) і однаковий масштаб осей (див. рис 1).
Кожній точці площини за певним правилом ставиться у відповідність пара чисел — абсциса та ордината (х; у). Ці числа називаються декартовими координатами точки.
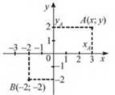 Рис. 1
Рис. 1
Правило визначення де картав их координат па площині
Через точку А проводимо пряму, паралельну осі ординат (ОУ), до перетину її з віссю абсцису точці хА. Число х, абсолютна величина якого дорівнює відстані від точки О до точки хА називається абсцисою точки А.
Через точку А проводимо пряму, паралельну осі абсцис (ОХ), до перетину її з віссю ординат у точці уА. Число у, абсолютна величина якого дорівнює відстані від точки О до точки уА, називається ординатою точки А.
Декартові координати точки записують у дужках поруч із буквеним позначенням точки А(х; у), причому першою в дужках стоїть абсциса, другою — ордината.
Початок координат О розділяє кожну вісь на дві піввісі, одна з яких вважається додатною, інша — від’ємною.
На рис. 1 точка А має координати 3 і 2, точка В — координати -2 і -2.
Будь-якій парі чисел х і у відповідає лише одна точка площини A (х; у).
Відстань між двома точками
Відстань між двома точками дорівнює квадратному кореню із суми квадратів різниці, однойменних координат.
Відстань міме двома точками на площині d = ![]() .
.
де d — відстань (рис. 2) між тoчкою А1 із координатами (х1;у1)і точкою А2 із координатами (X2; у2).
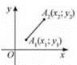 Рис. 2
Рис. 2
Координати середини відрізка
Координати середини відрізка дорівнюють півсумі відповідних координат його кінців.
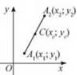 Координати середини відрізка на площині Координат (хС ∙ уС ) точки С, що є серединою відрізка, визначаються за формулами
Координати середини відрізка на площині Координат (хС ∙ уС ) точки С, що є серединою відрізка, визначаються за формулами
xC = ![]() ; yC =
; yC = ![]() .
.
де (х1;у1) і (х2;у2) — координат точок А1 і А2, що є кінцями Рис. 3
відрізка (рис. 3).
Рівняння фігури
Рівнянням фігури в декартових координатах на площині називається рівняння із двома невідомими х, у, які задовольняють координат будь-якої точки фігури, і тільки вони.
Рівняння кола
Якщо на площині задано деяку точку з координатами С (а; b), що є центром кола, а також радіус R (рис. 4), то рівняння кола має вигляд (х - a) + (у - b) = R2.
Якщо центром кола є початок координат (рис. 5), то маємо х2 +y2 = R2.
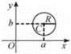 Рис. 4
Рис. 4
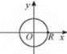 Рис. 5
Рис. 5
Рівняння прямої
Загальне повне рівняння будь-якої прямої у декартових координатах х, у має вигляд
ах + bу + с = 0, де а, b, с — деякі числа (рис. 6, а).
Якщо хоч один коефіцієнт у рівнянні прямої дорівнює нулю, рівняння називається неповним. Розташування прямої відносно осей координат залежить від коефіцієнтів а, b, с.
1. Якщо с = 0, а ≠ 0, b ≠ 0, то пряма ах + by = 0 проходить через початок координат (рис. 6, б).
2. Якщо а = 0, b ≠ 0, с ≠ 0, то пряма by + с = 0 проходите паралельно осі ОХ (рис. 6, в).
3. Якщо b = 0, а ≠ 0, с ≠ 0, то пряма ах + с = 0 проходить паралельно осі ОУ (рис. 6, г).
4. Якщо а ≠ 0, b = 0, с = 0, одержимо х = 0, що є рівнянням осі ОУ (рис. 6, д).
5. Якщо b ≠ 0, а = 0, с = 0, одержимо у = 0, що є рівнянням осі ОХ(рис, 6, е).
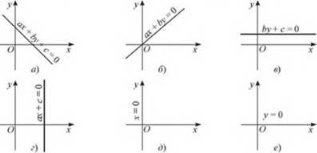 Рис. 6
Рис. 6
Якщо b * 0, то рівняння прямої можна записати у вигляді у = kх + b, де k — кутовий коефіцієнт прямої, k = tg![]() або k =
або k = ![]() (див. рис. 12)
(див. рис. 12) 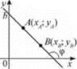 Рис. 7
Рис. 7
Умови паралельності двох прямих
Якщо прямі l та m задано відповідно рівняннями у = k1х + b1 і у = k2х + b2, то вони паралельні тоді і тільки тоді, коли k1 = k2 та b1 ≠ b2 (рис. 8).
Якщо k1 = k2 та b1 = b2, то прямі l та m збігаються. 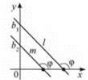 Рис. 8
Рис. 8
Умови перпендикулярності двох прямих Якщо прямі l та m задано відповідно рівняннями y = k1x + b1 і у = k2х + b2, то вони перпендикулярні тоді і тільки тоді, коли k1 ∙ k2 = -1 (рис. 9). 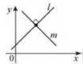 Рис. 9
Рис. 9
Перетворення фігур на площині
Симетрія (рис. 10)
|
Точки Симетрія відносно |
А (1; 1) |
А (х, у) |
|
точки О |
А1 (-1; -1) |
А1 (-х; -у) |
|
осі х |
A3 (1; -1) |
А3 (х;- у) |
|
осі у |
А2(-1; 1) |
А2 (-х; у) |
Рис. 10
Паралельне перенесення (рис. 11)
![]()
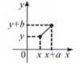 Рис. 11
Рис. 11
Гомотетія відносно точки О (рис. 12)
![]()
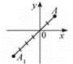 Рис. 12
Рис. 12
Поворот навколо точки О (рис. 13)
![]()
 Рис. 13
Рис. 13
Тема 20. Вектори на площині
Протилежні вектори
Вектор — напрямлений відрізок певної довжини, у якого один кінець вважається початком вектора, а інший — кінцем вектора.
Вектори позначаються двома великими латинським літерами зі стрілкою над ними або однією маленькою латинською літерою зі стрілкою над нею.
На рис. 1 зображено вектор ![]() (А — початок вектора, В — кінець вектора) та вектор
(А — початок вектора, В — кінець вектора) та вектор ![]() .
. 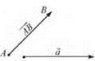 Рис. 1
Рис. 1
Координати вектора
Координати вектора ![]() що має початок у точці А і кінець у точці В, дорівнюють різниці відповідних координат точок В і А.
що має початок у точці А і кінець у точці В, дорівнюють різниці відповідних координат точок В і А.
Координати вектора на площині Якщо початком вектора є точка А(хАуА), а кінцем — точка В(xВ уВ), то ![]() (ХВ - ХА; УВ - УА) (рис. 2).
(ХВ - ХА; УВ - УА) (рис. 2). 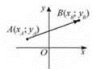 Рис. 2
Рис. 2
Довжина вектора
Довжина вектора (абсолютна величина або МОДУЛЬ) — довжина відрізка що зображує вектор. Позначення: |![]() |, |
|, |![]() |.
|.
Довжина вектора на площині
Якщо є вектор ![]() (а1; а2), то |
(а1; а2), то |![]() | =
| = ![]() , де |
, де |![]() | — модуль вектора, а1 і а2 — його координати.
| — модуль вектора, а1 і а2 — його координати.
Рівні вектори
Рівні вектори — вектори, які мають однаковий напрямок і рівні довжини.
На рис. 3 зображено рівні вектори ![]() і
і ![]() . Позначення:
. Позначення: ![]() = -
= -![]() .
.
Рівні вектори мають рівні координат. Якщо координати векторів рівні, то вектори рівні.
Рівність векторів на площині
Якщо ![]() (а1; а2) =
(а1; а2) = ![]() (b1; b2) то
(b1; b2) то ![]() Якщо
Якщо ![]() то
то ![]() (а1; а2) =
(а1; а2) = ![]() (b1; b2).
(b1; b2).
Протилежні вектори
Протилежні вектори — вектори, які мають протилежні напрямки і рівні довжини.
На рис. 4 зображено протилежні вектори ![]() і
і ![]() . Позначення:
. Позначення: ![]() = -
= -![]() .
.
Протилежні вектори мають протилежні відповідні координати. Якщо відповідні координати двох векторів протилежні, то вектори протилежні.
![]()
Рис. 3
Рис. 4
Якщо маємо ![]() (a1;a2),
(a1;a2), ![]() (b1;b2) і
(b1;b2) і ![]() = -
= -![]() , то
, то ![]()
Якщо маємо ![]() (a1;a2),
(a1;a2), ![]() (b1;b2) і
(b1;b2) і ![]() , то
, то ![]() = -
= -![]() .
.
Сума векторів
Нехай дано два вектори ![]() i
i ![]() (рис. 5).
(рис. 5).
Візьмемо довільну точку A і побудуємо вектор ![]() , що дорівнює
, що дорівнює ![]() .
.
Від точки
В відкладемо вектор ![]() , що дорівнює
, що дорівнює ![]() .
.
 Рис. 5
Рис. 5
Сумою векторів ![]() +
+ ![]() є вектор
є вектор ![]() (рис. 6), тобто вектор, що з’єднує початок першого вектора з кінцем другого (так зване правило трикутника).
(рис. 6), тобто вектор, що з’єднує початок першого вектора з кінцем другого (так зване правило трикутника).
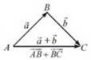 Рис. 6
Рис. 6
Для двох векторів (АО і ОС) зі спільним початком (О) їхня сума зображається діагоналлю паралелограма (ОВ), побудованого на цих векторах, до того ж початок вектора-суми збігаєтеся з початком цих векторів (рис. 7).  Рис. 7
Рис. 7
Сума векторів на площині ![]() (a1;a2) +
(a1;a2) + ![]() (b1;b2) =
(b1;b2) = ![]() (a1 + b1; a2 + b2).
(a1 + b1; a2 + b2).
Різниця векторів
Різницею векторів ![]() -
- ![]() є вектор
є вектор ![]() (рис. 8), тобто вектор, що з’єднує кінці векторів
(рис. 8), тобто вектор, що з’єднує кінці векторів ![]() i
i ![]() і напрямлений від від’ємника до зменшуваного.
і напрямлений від від’ємника до зменшуваного.
Координати різниці двох векторів дорівнюють різниці відповідних координат вектора — зменшуваного і вектора — від’ємника.
 Рис. 8
Рис. 8
Різниця векторів на площині ![]() (a1;a2)-
(a1;a2)- ![]() (b1;b2) =
(b1;b2) = ![]() (a1 – b1; a2 - b2).
(a1 – b1; a2 - b2).
Множення вектора на число
Добутком ![]()
![]() вектора
вектора ![]() на число
на число ![]() є вектор, довжина якого дорівнює |
є вектор, довжина якого дорівнює |![]() | ∙ |
| ∙ |![]() |, а напрямок — такий самий, що й у вектора
|, а напрямок — такий самий, що й у вектора ![]() якщо
якщо ![]() > 0, або протилежний напрямку вектора
> 0, або протилежний напрямку вектора ![]() , якщо
, якщо ![]() < 0 (рис. 9).
< 0 (рис. 9).
Якщо ![]() = 0 або
= 0 або ![]() =
= ![]() , то
, то ![]() =
= ![]() .
.
Координати вектора ![]()
![]() дорівнюють добутку числа), на відповідні координати вектора
дорівнюють добутку числа), на відповідні координати вектора ![]() .
.
![]() Рис. 9
Рис. 9
Множення вектора на число на площині ![]() ∙
∙ ![]() (а1; а2) =
(а1; а2) = ![]() (
(![]() а1;
а1; ![]() а2).
а2).
Колінеарні вектори
Два ненульові вектори називаються колінеарними, якщо вони лежать на одній прямій або на паралельних ПРЯМИХ.
На рис. 10 вектори ![]() ,
, ![]() ,
, ![]() — колінеарні.
— колінеарні.
Якщо вектори колінеарні, то їхні відповідні координати пропорційні. І навпаки, якщо відповідні координати двох векторів пропорційні, то ці вектори колінеарні.
![]() Рис.10
Рис.10
Колінеарність векторів на площині
Якщо є вектори ![]() (а1; а2),
(а1; а2), ![]() (b1; b2) і вони колінеарні, то
(b1; b2) і вони колінеарні, то ![]() =
= ![]() .
.
Якщо є вектори ![]() (a1;a2),
(a1;a2), ![]() (b1;b2) і
(b1;b2) і ![]() =
= ![]() , то
, то ![]() і
і ![]() — колінеарні вектори.
— колінеарні вектори.
Скалярний добуток двох векторів
Скалярним добутком двох векторів називається число, яке дорівнює сумі добутків відповідних
координат цих векторів. Позначення таке саме, як і для добутку чисел,— ![]() .
.
Скалярний добуток двох векторів на площині
Якщо є вектори ![]() (a1;a2),
(a1;a2), ![]() (b1;b2) то
(b1;b2) то ![]() ∙
∙ ![]() = a1b1 + a2b2.
= a1b1 + a2b2.
Теорема
Скалярний добуток двох векторів ![]() дорівнює добутку довжин цих векторів на косинус кута між ними (рис. 11). Отже,
дорівнює добутку довжин цих векторів на косинус кута між ними (рис. 11). Отже, ![]() =
= ![]() ∙ cos
∙ cos![]() .
.
Кут між двома векторами зі спільним початком визначається, як і звичайний кут.
Якщо є два довільні вектори ![]() і
і ![]() (рис. 12), то кутом між ними називається кут між рівними їм векторами зі спільним початком (рис. 13).
(рис. 12), то кутом між ними називається кут між рівними їм векторами зі спільним початком (рис. 13).
Кут між співнапрямленими векторами вважається таким, що дорівнює нулю.
Рис. 11
Рис. 12
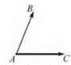
Рис. 13
Ознака перпендикулярності векторів
 Якщо вектори перпендикулярні (рис. 14), то їхній скалярний добуток дорівнює нулю.
Якщо вектори перпендикулярні (рис. 14), то їхній скалярний добуток дорівнює нулю.
І навпаки, якщо скалярний добуток відмінних від нуля векторів дорівнює нулю, то вектори перпендикулярні. Рис. 14
Алгебра. Тест до теми Натуральні числа та дії над ними
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Мотоцикліст їхав 3 год зі сталою швидкістю. Якщо він проїде ще 12 км із такою ж швидкістю, то його шлях буде дорівнювати 132 км. Із якою швидкістю їхав мотоцикліст?
|
А |
Б |
В |
Г |
Д |
|
20 км/год |
30 км/год |
40 км/год |
60 км/год |
45 км/год |
2. На подвір’ї гуляють кури, качки і гуси — разом 21 птах. Курей у 10 разів більше, ніж качок. Скільки на подвір’ї гусей?
|
А |
Б |
В |
|
Г |
|
Д |
|
1 |
3 |
7 |
|
10 |
|
12 |
|
|
|
|
|
|
||
3. Серед чисел 1113, 3040, 914, 7035, 7503 оберіть число, яке ділиться і на 3, і на 5.
|
А |
Б |
В |
Г |
Д |
|
1113 |
3040 |
914 |
7035 |
7503 |
4. Яку цифру із зазначених нижче треба поставити замість « у числі 5»62, щоб одержане число ділилося на 9?
|
А |
Б |
В |
Г |
Д |
|
0 |
2 |
9 |
3 |
5 |
5. Із поданих чисел оберіть число, яке ділиться і на 2, і на 3.
|
А |
Б |
В |
Г |
Д |
|
2894 |
406 |
2802 |
785 |
604 |
6. Найбільший спільний дільник чисел 144 і 168 дорівнює
|
А |
Б |
В |
Г |
Д |
|
12 |
24 |
34 |
1008 |
2016 |
7. Найменшим спільним кратним чисел 54,90 і 162 є число
|
А |
Б |
В |
Г |
Д |
|
270 |
180 |
810 |
1620 |
3240 |
8. Найменше спільне кратне чисел 144 і 168 дорівнює
|
А |
Б |
В |
Г |
Д |
|
24 |
288 |
1008 |
864 |
2016 |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний. на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між числовими виразами (1—4) та їхніми значеннями (А—Д).
|
1 |
78 + 23 ∙ 81 - 69 |
А |
354 |
|
2 |
78 + 23 ∙ (81 - 69) |
Б |
1212 |
|
3 |
(78 + 23) ∙ 81- 69 |
В |
1512 |
|
4 |
(78 + 23) ∙ (81 -69) |
Г |
1872 |
|
|
|
Д |
8112 |
Розв’яжіть завдання 10—12.
10. Знайдіть значення виразу (2356 + 809 - 2841) ∙ 106 : 159.
11. Знайдіть значення виразу 32087 - 87 ∙ (67 + 62524 : 308).
12. Знайдіть значення виразу ((451 - 17 ∙ 3) ∙ 3 - 200) : 500 + 46 ∙ 60.
Алгебра. Тест до теми Звичайні дроби, мішані числа та дії над ними
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Серед дробів ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() укажіть найменший.
укажіть найменший.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Серед дробів
 ,
, 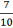 ,
, 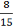 ,
, 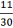 ,
,  укажіть найбільший
укажіть найбільший
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
3. Якщо швидкість човна проти течії становить 13![]() км/год, а швидкість течії — 2
км/год, а швидкість течії — 2![]() км/год, то власна швидкість човна дорівнює
км/год, то власна швидкість човна дорівнює
|
А |
Б |
В |
Г |
Д |
|
15 |
11 |
18 км/год |
15 |
16 км/год |
4. Якщо один кран заповнює басейн за 6 год, а другий — за 12 год, то за 1 год обидва крани заповнять
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
5. Сума дробів ![]() i
i ![]() дорівнює
дорівнює
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
6. Сума 3 ![]() = 4
= 4![]() дорівнює
дорівнює
|
А |
Б |
В |
Г |
Д |
|
8 |
7 |
8 |
7 |
7 |
7. Різниця 10 - 2![]() дорівнює
дорівнює
|
А |
Б |
В |
Г |
Д |
|
7 |
7 |
8 |
8 |
8 |
8. Значення виразу ![]() -
- ![]() дорівнює
дорівнює
|
А |
Б |
В |
Г |
Д |
|
1 |
|
|
|
|
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перегині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між числовими виразами (1—4) та їхніми значеннями (А—Д).
|
1 |
|
А |
- |
|
2 |
- |
Б |
|
|
3 |
|
В |
|
|
4 |
|
Г |
|
|
|
|
Д |
1 |
Розв’яжіть завдання 10—12.
10. Пшеницею засіяно 240 га, що становить ![]() усього поля. Знайдіть площу поля.
усього поля. Знайдіть площу поля.
11. У книзі 140 сторінок. Хлопчик прочитав ![]() цієї книги. Скільки сторінок прочитав хлопчик?
цієї книги. Скільки сторінок прочитав хлопчик?
12. Знайдіть значення виразу (( ![]() ) ∙
) ∙ ![]() + 6
+ 6![]() :
: ![]() ) : 1
) : 1![]() .
.
Алгебра. Тест до теми Десяткові дроби та дії над ними.
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише одна правильна. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку A.
1. Укажіть найменше серед даних чисел: 0,5005; 0,0505; 0,505; 0,055; 0,55.
|
А |
Б |
В |
Г |
Д |
|
0,5005 |
0,0505 |
0,505 |
0,055 |
0,55 |
- Знайдіть суму 3,084 + 15,62.
|
А |
Б |
В |
Г |
Д |
|
18,704 |
18,606 |
18,146 |
4,646 |
18,01 |
3. Наскільки 15,01 більше, ніж 12,3?
|
А |
Б |
В |
Г |
Д |
|
27,04 |
27,31 |
2,71 |
2,98 |
3,02 |
4. Швидкість потягу становить 84,5 км/год. Який шлях пройде потяг за 3,5 год?
|
А |
Б |
В |
Г |
Д |
|
29,575 км |
295,75 км |
295,5 км |
29575 км |
29,55 км |
5. Брат і сестра зробили покупку на 90 грн. Брат заплатив 0,3 від вартості покупки, а сестра — решту грошей. Скільки грошей заплатила сестра за покупку?
|
А |
Б |
В |
Г |
Д |
|
27 грн |
30 грн |
60 грн |
63 грн |
65 грн |
6. Швидкість слимака — м/хв. Знайдіть його швидкість у кілометрах за годину.
|
А |
Б |
В |
Г |
Д |
|
0,5 км/год |
0,05 км/год |
5 км/год |
0,005 км/год |
0,002 км/год |
7. Швидкість тіла становить 24 м/с. Знайдіть цю швидкість у кілометрах за годину.
|
А |
Б |
В |
Г |
Д |
|
1,44 км/год |
3,6 км/год |
86,4 км/год |
150 км/год |
24 000 км/год |
8. Купили 3 кг яблок по 2,5 грн за 1 кг та 4 кг груш. За груші заплат ли на 1,5 грн менше, ніж за яблука. Скільки коштує 1 кг груш?
|
А |
Б |
В |
Г |
Д |
|
1,5 грн |
2,5 грн |
3,5 грн |
4,5 грн |
5 грн |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перегині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між числовими виразами (1—1) та їхніми значеннями (А—Д).
|
1 |
0,3 + 0,5 |
А |
-0,2 |
|
2 |
0,3 - 0,5 |
Б |
0,15 |
|
3 |
0,3 ∙ 0,5 |
В |
0,5 |
|
4 |
0,3 : 0,5 |
Г |
0,6 |
|
|
|
Д |
0,8 |
Розв’яжіть завдання 10—12.
10. Автомобіль проїхав 298 км із постійною швидкістю за 4 год. Скільки кілометрів проїде автомобілі» за 5 год, рухаючись із такою ж швидкістю?
11. Власна швидкість човна 24,6 км/год, швидкість течії річки — 2,9 км/год. Скільки кілометрів пропливе човен, рухаючись 2 год за течією і 3 год проти течії?
12. Швидкість човна в стоячій воді становить 15,3 км/год а швидкість течії річки 1,5 км/год. Скільки кілометрів пропливе човен, рухаючись 2 год проти течії і 3 год за течією?
Алгебра. Тест до теми Раціональні числа та дії над ними.
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильні. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Знайдіть значення виразу ![]()
|
А |
Б |
В |
Г |
Д |
|
|
- |
|
|
1 |
2. Знайдіть значення виразу ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
- |
|
- 1 |
1 |
2 |
3. Знайдіть значення виразу ![]() – (
– (![]() +
+ ![]() ) : 2 +
) : 2 + ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
-2 |
- 1 |
0 |
1 |
2 |
4. На карті, масштаб якої 1 : 600 000, відстань між Харковом та Ізюмом дорівнює 18 см. Знайдіть цю відстань па місцевості.
|
А |
Б |
В |
Г |
Д |
|
100 км |
105 км |
108 км |
110 км |
107 км |
5. Довжина хвилинної стрілки годинника 2 см, годинникової стрілки — 1,5 см. У скільки разів швидкість кінця хвилинної стрілки більше швидкості кінця годинникової стрілки?
|
А |
Б |
В |
Г |
Д |
|
у 2 рази |
у 4 рази |
у 8 разів |
у 16 разів |
у 18 разів |
6. Швидкість пароплава відноситься до швидкості течії ріки як 36 : 5. Пароплав рухався за течією 5 год 10 хв. Скільки часу потрібно йому, щоб повернутися назад?
|
А |
Б |
В |
Г |
Д |
|
6 год |
6 год 25 хв |
6 год 30 хв |
6 год 50 хв |
6 год 55 хв |
7. Рівність ![]() =
= ![]() справедлива, якщо у дорівнює
справедлива, якщо у дорівнює
|
А |
Б |
В |
Г |
Д |
|
12 |
15 |
18 |
24 |
32 |
8. За 6 однакових стільців сплатили 267 гри. Скільки гривень треба сплатити за 5 таких самих стільців?
|
А |
Б |
В |
Г |
Д |
|
200,5 грн |
210,5 грн |
222,5 грн |
250 грн |
275,5 грн |
За 6 однакових стільців сплатили 267 гри. Скільки гривень треба сплатити за 5 таких самих стільців?
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між числовими виразами (1—4) та їхніми значеннями (А—Д).
|
1 |
28 - 4 ∙ (25 - 33) - 100 |
А |
-2592 |
|
2 |
28 - 4 ∙ (25 - 33 - 100) |
Б |
-292 |
|
3 |
(28 - 4) ∙ (25 - 33) - 100 |
В |
-40 |
|
4 |
(28 - 4) ∙ (25 - 33 - 100) |
Г |
140 |
|
|
|
Д |
460 |
Розв’яжіть завдання 10—12.
10. Знайдіть значення виразу (1![]() + 2
+ 2![]() ) ∙ (1
) ∙ (1![]() -
- ![]() ); (1
); (1![]() + 2
+ 2![]() +
+ ![]() ) +
) + ![]() .
.
11. Знайдіть значення виразу 1![]() – 3,4(12) -
– 3,4(12) - ![]() +
+ ![]() (
(![]() + 0,5 - 3
+ 0,5 - 3![]() ) +
) + ![]() .
.
12. Знайдіть значення виразу 3![]() ∙
∙ ![]() – (2,(4) ∙ 2
– (2,(4) ∙ 2![]() ) : (-
) : (-![]() ).
).
Алгебра. Тест до теми Відсотки. Задачі на відсотки.
Завдання 1—8 мають по п'ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Виразіть у відсотках число 0,125.
|
А |
Б |
В |
Г |
Д |
|
1,25% |
12,5% |
125% |
0,125% |
0,0125 % |
2. Виразіть у вигляді дробу 2,45 %.
|
А |
Б |
В |
Г |
Д |
|
2,45 |
0,245 |
0,0245 |
0,00245 |
245 |
3. Із молока одержують 10 % сиру. Скільки сиру можна одержати із 40 кг молока?
|
А |
Б |
В |
Г |
д |
|
5 кг |
4 кг |
2 кг |
1 кг |
0,4 кг |
4. Цукровий буряк містить 10 % цукру. Скільки кілограмів цукрових буряків треба переробиш, щоб одержати 4 кг цукру?
|
А |
Б |
В |
Г |
Д |
|
50 кг |
40 кг |
20 кг |
0,4 кг |
10 кг |
5. Визначте відсоток солі у розчині, якщо відомо, що в 300 г розчину міститься 15 г солі.
|
А |
Б |
В |
Г |
Д |
|
20% |
15% |
10% |
5% |
2% |
6. Вкладник поклав до банку 400 гри під 3% річних. Яким буде його вклад через 2 роки?
|
А |
Б |
В |
Г |
Д |
|
406 грн |
424,36 грн |
442,25 грн |
484,75 грн |
500 грн |
7. Вкладник поклав до банку деяку суму грошей під 3 % річних. Через рік його вклад становив 576.8 гри. Скільки гривень становив початковий внесок вкладника?
|
А |
Б |
В |
Г |
Д |
|
520 грн |
530 грн |
540 грн |
550 грн |
560 грн |
8. Ціна автомобіля спочатку зросла на 10 %, а потім знизилася на 20 %. Як і на скільки відсотків зміниться ціна автомобіля після двох переоцінок?
|
А |
Б |
В |
Г |
Д |
|
збільшиться на 10% |
зменшиться на 10% |
не зміниться |
зменшиться на 12% |
збільшиться на 12% |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність десяткових дробів (1—4) із відсотками (А—Д).
|
1 |
0,02 |
А |
2% |
|
2 |
0,05 |
Б |
5% |
|
3 |
0,2 |
В |
20% |
|
4 |
0,5 |
Г |
50% |
|
|
|
Д |
100% |
Розв’яжіть завдання 10—12.
10. За три дні продали 320 коробок цукерок. За перший день продали 40 % цієї кількості, за другий — ![]() решти. Скільки коробок цукерок продали за третій день?
решти. Скільки коробок цукерок продали за третій день?
11. Три класи посадили дерева вздовж дороги. Перший клас посадив 35 % усіх дерев, другий клас посадив ![]() остачі, а третій клас решту — 104 дерева. Скільки дерев посадили три класи разом?
остачі, а третій клас решту — 104 дерева. Скільки дерев посадили три класи разом?
12. Твердий припой для паяльних робіт — сплав, який містить 45 % срібла, 30 % міді і 25 % цинку. Скільки тонн міді слід взяти, щоб приготувати 9 т твердого припою?
Алгебра. Тест до теми Степінь з натуральним і цілим показником
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Яка з поданих рівностей правильна?
|
А |
Б |
В |
Г |
Д |
|
11-2 = |
(-3)-4 = |
(3 |
( |
|
2. Який із поданих виразів тотожно дорівнює виразу 5х-3у2?
|
А |
Б |
В |
Г |
Д |
|
|
|
- |
|
|
3. Обчисліть (-1)2n+1 ∙ (-1)6, де n - натуральне число.
|
А |
Б |
В |
Г |
Д |
|
1 |
0 |
-1 |
7 |
(-1)n |
4. Яка з рівностей є неправильною?
|
А |
Б |
В |
Г |
Д |
|
8-5 ∙ 83 = |
13-7 : 13-9 = 169 |
125 : 124= 12 |
(5-1)2 = - |
6а9 ∙ 4а13 = 24а4 |
5. Число 45 000 можна записати у стандартному вигляді
|
А |
Б |
В |
Г |
Д |
|
4,5 ∙ 103 |
0,45 ∙ 105 |
45 ∙ 103 |
4,5 ∙ 104 |
45 ∙ 10-3 |
6. Число 2,5 ∙ 10-2 можна записати у вигляді десяткового дробу
|
А |
Б |
В |
Г |
Д |
|
0,025 |
0,0025 |
0,25 |
0,00025 |
2,5 |
7. Число ![]() можна записати у вигляді степеня з основою 2
можна записати у вигляді степеня з основою 2
|
А |
Б |
В |
Г |
Д |
|
2-5 |
24 |
2-6 |
26 |
25 |
8. Вираз ![]() можна записати у вигляді добутку
можна записати у вигляді добутку
|
А |
Б |
В |
Г |
Д |
|
8Х3 |
8Х-3 |
(8х)3 |
(2х)-3 |
(8х)-3 |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний. на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. До кожного виразу (1—4) доберіть тотожно йому рівний вираз (А—Д).
|
1 |
(а5а6)2 |
А |
а10 |
|
2 |
( |
Б |
а12 |
|
3 |
(а4)2 ∙ (а2)4 |
В |
а15 |
|
4 |
|
Г |
а16 |
|
|
|
Д |
а22 |
Розв’яжіть завдання 10—12.
10. Обчисліть ![]() .
.
11. Обчисліть ![]() .
.
12. Яка остання цифра числа є закінченням виразу 145х + 131у + 146х+у, якщо х ∈ N, y ∈ N?
Алгебра. Тест до теми Одночлени та дії над ними
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Якщо а = 10, b = -10, то значення виразу 3а - 3b дорівнюватиме
|
А |
Б |
В |
Г |
Д |
|
30 |
60 |
-30 |
-60 |
0 |
2. Знайдіть значення виразу –а + 2![]() а, якщо а =
а, якщо а = ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
0 |
- |
|
1 |
|
3. Вираз (2![]() х3у) ∙ (
х3у) ∙ (![]() ху2)2 тотожно дорівнює одночлену
ху2)2 тотожно дорівнює одночлену
|
А |
Б |
В |
Г |
Д |
|
х4у5 |
2 |
|
|
х5у5 |
4. Добуток одночленів (![]() а2b3x) ∙ (
а2b3x) ∙ (![]() a3bx2) дорівнює
a3bx2) дорівнює
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
5. Рівність (3![]() m4)n ∙ 0,001=
m4)n ∙ 0,001= ![]() m12 справедлива, якщо n дорівнює
m12 справедлива, якщо n дорівнює
|
А |
Б |
В |
Г |
Д |
|
16 |
10 |
8 |
3 |
0 |
6. Формулою натурального числа, кратного 3, є
|
А |
Б |
В |
Г |
Д |
|
3 + n, n ∈ N |
3 - n, n ∈ N |
3n, n ∈ N |
|
3n - n, n ∈ N |
7. Одночлен -1000х15у21 записують у вигляді куба одночлена
|
А |
Б |
В |
Г |
Д |
|
(10х12у18)3 |
(-10х5у7)3 |
(10х5у7)3 |
(-10х12у18)3 |
(-10х5у18)3 |
8. Знайдіть змінну р із формули m = рV.
|
А |
Б |
В |
Г |
Д |
|
p = |
p = mV |
p = m - V |
p = |
p = m + V |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний. на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між заданими виразами (1—4) та степенями, що їм тотожно дорівнюють (А—Д).
|
1 |
(x2)3x |
А |
x2 |
|
2 |
(х2х3)2 |
Б |
x2 |
|
3 |
(x3 : х2)2 |
В |
x5 |
|
4 |
( |
Г |
x7 |
|
|
|
Д |
x10 |
Розв’яжіть завдання 10—12.
10. Спростіть вираз ![]() ∙
∙ ![]() та знайдіть його значення, якщо х = у = 5.
та знайдіть його значення, якщо х = у = 5.
11. Спростіть вираз (![]() )-3 ∙ (
)-3 ∙ (![]() )2 та знайдіть його значення, якщо х = у = 3.
)2 та знайдіть його значення, якщо х = у = 3.
12. При якому значенні х правильною є рівність (![]() )-5= 0?
)-5= 0?
Алгебра. Тест до теми Многочлени та дії над ними
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Купили 5 кг цукерок за ціною а грн. за 1 кг і 3 кг цукерок за ціною 6 грн за 1 кг. Запишіть у вигляді виразу вартість покупки.
|
А |
Б |
В |
Г |
Д |
|
5а + 3b |
8(а + b) |
5b + 3а |
5а - 3b |
15аb |
2. Вираз 5ах + bх + 5ay + by можна записати у вигляді добутку
|
А |
Б |
В |
Г |
Д |
|
(5ax + 6x)(5ay + by) |
(5а + x)(b + у) |
(5а + у)(х + b) |
(5а - b)(x - у) |
(5а + b)(x + у) |
3. Вираз 4x2 - 5x - (9 + 3x2 + 8x) тотожно дорівнює
|
А |
Б |
В |
Г |
Д |
|
7х2 - 3х + 9 |
х2 - 1Зх - 9 |
х2 - 13x + 9 |
7x2 + 3x + 9 |
х2 + 3х - 9 |
4. Розкрийте дужки у виразі -4(2а - 3).
|
А |
Б |
В |
Г |
Д |
|
8а - 12 |
8а + 12 |
-8а + 12 |
-8а - 12 |
4а |
5. Вираз (х - 1 )(х - 3) тотожно дорівнює
|
А |
Б |
В |
Г |
Д |
|
х2 - 2x + 3 |
x2 + 4x + 3 |
x2 - 4x - 3 |
х2 - 4х + 3 |
x2 + 4x - 3 |
6. Квадрат різниці виразів 7х і у дорівнює
|
А |
Б |
В |
Г |
Д |
|
49x2 - 7ху + у2 |
49x2 - у2 |
49x2 + 14xу + у2 |
7x2 - 4xу + у2 |
49x2 - 14xу + у2 |
7. Многочлен а3 + 64 тотожно дорівнює добутку
|
А |
Б |
В |
Г |
Д |
|
(а + 4)(а2 + 4а + 16) |
(а - 4)(а2 + 4а + 16) |
(2а - 8)(а + 8) |
(а+ 4)(а2 - 8а + 16) |
(а +4)(а2 - 4а + 16) |
8. Винесіть за дужки спільний множнику виразі 12а- 16b.
|
|
|
|
|
|
||||
|
А |
Б |
В |
Г |
Д |
||||
|
4(а - 16b) |
4(3а - 4b) |
4(а - 4b) |
4(3а + 4b) |
12(а - 4b) |
||||
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перегині відповідних рядків (цифри) і колонок (букви).
9. До кожного виразу (1—4) доберіть тотожно йому рівний вираз (А—Д).
|
1 |
(х - у)2 + (х + у)2 |
А |
2x3+ bxу2 |
|
2 |
(х + y)2 - (х - у)2 |
Б |
- 6x2у - 2y3 |
|
3 |
(х - у)3 + (х + у)3 |
В |
-4xу |
|
4 |
(Х - у)3 -(Х + у)3 |
Г |
4ху |
|
|
|
Д |
2х2 + 2y2 |
Розв'яжіть завдання 10—12.
10. Знайдіть значення виразу 0,992, використовуючи формулу скороченого множення.
11. Знайдіть значення виразу 88 ∙ 0,15 + 0,45 ∙ 88 + 12 ∙ 0,16 + 12 ∙ 0,44 найбільш раціональним способом (без калькулятора).
12. При якому значенні х: значення виразу х2 - 8х + 17 є найменшим?
Алгебра. Тест до теми Алгебраїчні дроби та дії над ними.
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. При яких значеннях змінної а вираз ![]() не має змісту?
не має змісту?
|
А |
Б |
В |
Г |
Д |
|
-2 |
2 |
-3 |
3 |
0 |
Увага! Перетворення виразів у завданнях № 2—8 виконуємо на множині всіх допустимих значень змінної (змінних), що входять до них.
2. Скоротіть дріб 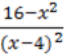 .
.
|
А |
Б |
В |
Г |
Д |
|
-1 |
|
|
|
1 |
3. Якщо ![]() = 3, то
= 3, то ![]() дорівнює
дорівнює
|
А |
Б |
В |
Г |
Д |
|
1 |
2 |
3 |
4 |
5 |
4. Спростіть вираз ![]() -
- ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
|
0 |
4 |
|
|
5. Спростіть вираз ![]() -
- ![]() -
- ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
a - 1 |
a + 1 |
6. Виконайте множення дробів ![]() ∙
∙ ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
7. Спростіть вираз ![]() :
: ![]() :
: ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
8. Виконайте ділення дробів ![]() :
: ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між раціональними виразами (1—4) та раціональними виразами (А—Д), що є тотожно рівними на всій області їх визначення.
|
1 |
|
А |
|
|
2 |
|
Б |
|
|
3 |
|
В |
a |
|
4 |
|
Г |
b |
|
|
|
Д |
-a-b |
Розв'яжіть завдання 10-—12.
10. Перший і другий крани наповнюють ванну водою за 20 хвилин, другий і третій — за 15 хвилин, а перший і третій — за 12 хвилин. За скільки хвилин наповнять таку ж ванну три крани, працюючи разом?
11. Знайдіть значення виразу (![]() ) ∙ (х2 + х + 1), якщо х = 99.
) ∙ (х2 + х + 1), якщо х = 99.
12. Знайдіть значення виразу (ух-1 - ху-1) : (2 - ху-1 - ух-1) : (ух-1 + 1), якщо х = 99, у = - 1.
Алгебра. Тест до теми Арифметичний квадратний корінь. Дійсні числа.
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Укажіть правильне твердження.
|
А |
Б |
В |
Г |
Д |
|
найменшого натурального числа не існує |
Кожне дійсне число є раціональним |
кожне раціональне число є цілим |
Кожне просте число є непарним |
кожне раціональне число є дійсним |
2. Значення якого з поданих виразів дорівнює 1![]() ?
?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
3. Яке з поданих чисел є найбільшим?
|
А |
Б |
В |
Г |
Д |
|
4,(62) |
3,(3) |
-2,75 |
-2,(63) |
4,623 |
4. Значення якого з поданих виразів дорівнює 14?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
5. Знайдіть наближене значення виразу а + b, де а = 1,0539... і b = 2,0610.... попередньо округливши а і b до тисячних.
|
А |
Б |
В |
Г |
Д |
|
3,113 |
3,114 |
3,115 |
3,116 |
3,117 |
6. Між якими цілими послідовними числами міститься число ![]() ?
?
|
А |
Б |
В |
Г |
Д |
|
5 і 6 |
6 і 7 |
7 і 8 |
8 і 9 |
9 і 10 |
7. Яке з наведених тверджень неправильне?
|
А |
Б |
В |
Г |
Д |
|
сума двох ірраціональних чисел може бути раціональним числом |
сума двох простих чисел може бути простим числом |
частка двох ірраціональних чисел може бути раціональним числом |
добуток двох ірраціональних чисел може бути раціональним числом |
добуток раціонального та ірраціонального чисел може бути раціональним числом |
8. Спростіть вираз -5у6 ![]() , якщо у < 0.
, якщо у < 0.
|
А |
Б |
В |
Г |
Д |
|
-5у7 |
-5у8 |
5у8 |
5у7 |
5у12 |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний. на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між виразами (1—4) та їхніми числовими значеннями (А—Д).
|
1 |
|
А |
2 |
|
2 |
|
Б |
4 |
|
3 |
|
В |
5 |
|
4 |
|
Г |
9 |
|
|
|
Д |
26 |
Розв’яжіть завдання 10—12.
10. Знайдіть значення виразу ![]() 2 +
2 + ![]() 2.
2.
11. Знайдіть значення виразу ![]() +
+ ![]() .
.
12. Знайдіть значення виразу ![]() ∙ (
∙ (![]() +1).
+1).
Алгебра. Тест до теми Рівняння, нерівності та їх системи.
Завдання 1—8 мають по п’яти варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Яке з поданих чисел є коренем рівняння х2 - 5х - 6 = 0?
|
А |
Б |
В |
Г |
Д |
|
-6 |
-1 |
0 |
1 |
2 |
2. Розв’язком якої з наведених нерівностей є число 1?
|
А |
Б |
В |
Г |
Д |
|
х2 - х > 0 |
3х + 2 < 0 |
- 5х + 1 > 0 |
х2- 1 >0 |
2х+ 1 >0 |
3. Укажіть пару рівносильних нерівностей.
|
А |
Б |
В |
Г |
Д |
|
3х + 2 > 0 |
3х ≤ 6 |
-2х ≥ 6 |
(х + 1)2 > 0 |
3х + 2 > 0 |
|
та 2х > -3 |
та х ≥ 2 |
та х ≥ -3 |
та х + 1 > 0 |
та 3х > -2 |
4. Коренем якого з наведених рівнянь є будь-яке число?
|
А |
Б |
В |
Г |
Д |
|
х2 = 1 |
х2 =-1 |
х2 = х2 |
х2 = 0 |
х2 = х |
5. Яка з наведених пар чисел є розв’язком рівняння ху + у= 10?
|
А |
Б |
В |
Г |
Д |
|
(-2; 10) |
(1; 10) |
(2; 4) |
(3; 2,5) |
(10; 0) |
6. Яке з рівнянь є лінійним рівнянням із двома змінними?
|
А |
Б |
В |
Г |
Д |
|
ху + 2х = 9 |
х2 - 2у = 5 |
х - 2у2 = 3 |
3х - у = 7 |
х2 + у3 = 0 |
7. Графіком якого з поданих рівнянь є пряма, паралельна осі Ох?
|
А |
Б |
В |
Г |
Д |
|
0х + 0у = 0 |
3х + 0у = 15 |
0х + 2у = 8 |
0х + 0у = 7 |
2х - 3у = 0 |
8. Укажіть правильну з наведених нерівностей.
|
А |
Б |
В |
Г |
Д |
|
|
3 ≥ |
- |
2- |
2+ |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перегині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між рівняннями (1—4) та їх коренями (А—Д).
|
1 |
5х + 8 = 3 |
А |
-2 |
|
2 |
5х - 3 = 2 |
В |
-1 |
|
3 |
3х - 5 = 1 |
В |
0 |
|
4 |
3х + 5 = 5 |
Г |
1 |
|
|
|
Д |
2 |
Розв’яжіть завдання 10—12.
10. Розв’яжіть рівняння 5х + 3 = 27 - 3х.
11. Яке найбільше ціле значення n задовольняє нерівність 7n - 13 ≤ 5n - 9?
12. Розв’яжіть рівняння |x + 2| ∙ (-х + 1) = 0. Якщо рівняння має декілька коренів, то у відповідь запишіть їхню суму.
Алгебра. Тест до теми Функції та їх основні властивості
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Задано функцію f(х) = ![]() . Знайдіть f(0): f(1).
. Знайдіть f(0): f(1).
|
А |
Б |
В |
Г |
Д |
|
-0,5 |
0 |
0,5 |
1 |
2 |
2. Знайдіть область визначення функції у = ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
(-∞; +∞) |
(-∞; 1) |
(-∞; -1) |
(-1; 1) |
[-1; 1] |
3. Знайдіть області, визначення функції у = ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
(-∞; +∞) |
(-∞; 1) |
(-∞;-1) |
(-1; 1) |
[-1; 1] |
4. Знайдіть області, визначення функції y = ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
[6; + ∞) |
[-6; + ∞) |
(-∞; 6] |
(-∞; + ∞) |
(-∞; -0] |
5. На рисунку зображено точку, через яку проходить графік функції у = f(х). Укажіть функцію у = f(х).
|
А |
Б |
В |
Г |
Д |
|
у = х + 3 |
y = x - 3 |
у = х + 2 |
у = -x + 1 |
у = х - 2 |
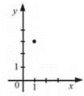
6. На рисунку зображено графік функції у = f(х), заданої на проміжку [-2; 4]. Знайдіть проміжок, на якому функція спадає.
|
А |
Б |
В |
Г |
Д |
|
[-2; 4] |
[-2; 0] |
[-2; 2] |
[0; 4] |
[2; 4] |
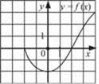
7. Функціям = f(x) визначена на всій числовій прямій і є періодичною з найменшим додатним періодом 6. На рисунку зображено графік функції на відрізку [-3; 3]. Обчисліть f(6) ∙ f(8).
|
А |
Б |
В |
Г |
Д |
|
-3 |
0 |
1 |
2 |
3 |
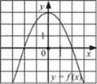
8. Функція у = f(x) — спадна, а = f(10), b = f(-10), с = f(0). Порівняйте а, b і с.
|
А |
Б |
В |
Г |
Д |
|
а > b > с |
с > b > а |
а > с > b |
b > а > с |
b > с > а |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. На рисунку зображено графік функції y = f(x). Установіть відповідність між властивостями функції (1—4) та проміжками (А—Д).
|
1 |
Область значень функції f = f(x) |
А |
[- 3; - 1) |
|
2 |
Області, визначення функції f = f(x) |
Б |
(-1; 3) |
|
3 |
Множина всіх значень х, при яких функція від’ємна |
В |
[-2; 1] |
|
4 |
Множина всіх значень х, при яких функція додатна |
Г |
(0; 2] |
|
|
|
Д |
[- 3; 3] |
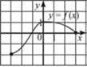
Розв’яжіть завдання 10—12.
10. Розв’яжіть графічно рівняння ![]() = x.
= x.
11. Знайдіть значення функції у = ![]() .
.
якщо значення аргументу дорівнює 1.
12. Знайдіть значення аргументу, при якому значення функції у = ![]() дорівнює 1.
дорівнює 1.
Алгебра. Тест до теми Лінійна функція, лінійні ріння, нерівності та їх системи..
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильні; на Вашу думку, відповідь і позначте її у бланку А.
1. Розв’язком якого з наведених рівнянь є будь-яке число?
|
А |
3(2X + 3) - 2(3x - 2) = 0 |
|
Б |
3(2x + 3) + 2(3x - 2) = 0 |
|
В |
3(2x - 2) - 2(2x - 3) = 0 |
|
Г |
3(2x - 2) + 2(2x - 3) = 0 |
|
Д |
3(2x + 3) - 3(2x + 3) = 0 |
2. Розв’яжіть рівняння |x + 5| = 6 та знайдіть суму його коренів.
|
А |
Б |
В |
Г |
Д |
|
-12 |
-11 |
-10 |
10 |
12 |
3. Скільки розв’язків має рівняння ||x|-5| = 1?
|
А |
Б |
В |
Г |
Д |
|
жодного |
один |
два |
три |
чотири |
4. Розв’яжіть рівняння ![]() -
- ![]() =
= ![]() -
- ![]() та укажіть, якому з наведених проміжків належить його корінь.
та укажіть, якому з наведених проміжків належить його корінь.
|
А |
Б |
В |
Г |
Д |
|
(- 6; - 3) |
(-3; 0) |
(0; 2) |
(2; 4) |
(4; 6) |
5. При якому значенні параметра а рівняння (а2 - 9)х = (а - 1 )(а + 3) не має коренів?
|
А |
Б |
В |
Г |
Д |
|
а =-3 |
а = -1 |
а = 3 |
а = 3 і а = -1 |
а = 1 і а = -3 |
6. Розв’яжіть нерівність 2(3 - х) - 3(2 + х) ≤ х.
|
А |
Б |
В |
Г |
Д |
|
[0;+∞) |
(-∞; 0] |
[-5; +∞) |
(∞;-5] |
(-1;+∞) |
7. Розв’язком якої з поданих нерівностей є множина всіх дійсних чисел?
|
А |
Б |
В |
Г |
Д |
|
0x ≤ - 6 |
0x > 6 |
0x ≤ 0 |
0x > 0 |
0x < 0 |
8. Розв’яжіть нерівність х —![]() ≤
≤ ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
|
(-∞;5] |
[5;+∞) |
[-5;+∞) |
[1;+∞) |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку; варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перегині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між нерівністю (1—4) та її розв’язком (А—Д).
|
1 |
8х + 2 < 9х - 3 |
А |
(-∞; |
|
2 |
6у + 8 ≤ 10у - 8 |
Б |
(-∞;4) |
|
3 |
3 – 11у ≥ - 3у + 6 |
В |
[4;+∞) |
|
4 |
3m – 1 ≤ 1,5m + 5 |
Г |
(5;+∞) |
|
|
|
Д |
(-∞;4] |
Розв’яжіть завдання 10—12.
10. Розв’яжіть рівняння ![]() -
- ![]() =
= ![]() .
.
11. На першому складі — 51 т вугілля, а на другому — 12 т. Скільки тонн вугілля треба перевезти з першого складу на другий, щоб на першому складі стало вугілля вдвічі більше, ніж на другому?
12. Вкладник зняв із рахунку в банку 20% усіх грошей, а через годину — 30 % залишку. Після цього на його рахунку залишилося 280 грн. Яким був початковий вклад (у грн)?
Алгебра. Тест до теми Квадратична функція, квадратні рівняння, нерівності та їх системи
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Скільки коренів має рівняння 6х2 + 13х + 10 = 0?
|
А |
Б |
В |
Г |
Д |
|
жодного |
один |
два |
три |
безліч |
2. Яке з наведених рівнянь має два різних корені?
|
А |
Б |
В |
Г |
Д |
|
х2 - 3х + 4 = 0 |
х2 - 3х + 2 = 0 |
х2 - 2x + 2 = 0 |
х2 - 2х + 1 = 0 |
х2 + 3х + 3 = 0 |
3. Добуток коренів рівняння 3x2 - 16x + 6 = 0 дорівнює
|
А |
Б |
В |
Г |
Д |
|
-16 |
2 |
-6 |
6 |
16 |
4. Розв’яжіть рівняння х2 - 10x - 24 = 0 та знайдіть різницю між більшим і меншим коренями.
|
А |
Б |
В |
Г |
Д |
|
-10 |
-14 |
0 |
14 |
10 |
5. Користуючись графіком функції у = х2 - 4х + 3, розв’яжіть нерівність х2 - 4х + 3 < 0.
|
А |
Б |
В |
Г |
Д |
|
(∞; 1) |
(3; +∞) |
(-∞; 1 ) |
(1; 3) |
(-∞; 2) |
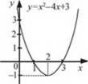
6. Укажіть пару рівносильних нерівностей.
|
А |
|
|
Б |
|
|
В |
|
|
Г |
|
|
Д |
|
7. Знайдіть область визначення функції y = ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
(∞;1) |
(∞;1] |
(1; 3) |
[1; 3] |
(—∞;+∞) |
8. Схематично зобразіть графіки рівнянь і з’ясуйте, яка із систем не має розв’язків.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між указаними геометричними перетвореннями (1—4) графіка функції у = x2 + 1 та відповідними функціями (А—Д).
|
1 |
Якщо графік функції у = x2 + 1 перенести на одиницю вправо вздовж осі ОХ, то отримаємо графік функції |
А |
у = x2 |
|
2 |
Якщо графік функції у = х2 + 1 перенести на одиницю вниз уздовж осі ОY, то отримаємо графік функції |
Б |
у = x2 + 2 |
|
3 |
Якщо графік функції у = x2 + 1 перенести на одиницю вліво вздовж осі ОХ, то отримаємо графік функції |
В |
y = (х- 1)2 + 1 |
|
4 |
Якщо графік функції у = x2 + 1 перенести на одиницю вгору уздовж осі ОY, то отримаємо графік функції |
Г |
у = (x + 1)2 + 1 |
|
|
|
Д |
y = (x + 1)2 - 1 |
Розв’яжіть завдання 10—12.
10. При якому значенні параметра к графіки функцій у = kх - 3 і у - х2 перетинаються в точці, абсциса якої дорівнює - 2?
11. Складіть зведене квадратне рівняння, корені якого дорівнюють 2 - ![]() i 2 +
i 2 + ![]() . Укажіть коефіцієнт при х.
. Укажіть коефіцієнт при х.
12. Серед коренів рівняння (x2 + х + 1 )(х2 + x + 3) = 15 укажіть найменший.
Алгебра. Тест до теми Раціональні рівняння, нерівності та їх системи
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Скільки коренів має рівняння ![]() = 0?
= 0?
|
А |
Б |
В |
Г |
Д |
|
жодного |
один |
два |
три |
безліч |
2. Розв’яжіть нерівність х2 < х.
|
А |
Б |
В |
Г |
Д |
|
(-∞; 0) |
(-∞; 1) |
(-∞; 0) |
(0; 1) |
(1; +∞) |
3. Розв’яжіть нерівність ![]() > 0.
> 0.
|
А |
Б |
В |
Г |
Д |
|
(-∞; 1) |
(1; +∞) |
(-∞;1) |
(1; 6) |
(-∞; 1 ) |
4. Розв’яжіть нерівність ![]() ≥ 0.
≥ 0.
|
А |
Б |
В |
Г |
Д |
|
(-∞; 0) |
[-2; +∞) |
(-∞;-2] |
[-2; 0) |
(-∞; -2) |
5. Розв’яжіть нерівність ![]() > 1.
> 1.
|
А |
Б |
В |
Г |
Д |
|
(-∞; 0) |
(-∞; 1) |
(-∞;-1) |
(-1; 1) |
(-1;0) |
6. Розв’яжіть нерівність ![]() ≤ 0.
≤ 0.
|
А |
Б |
В |
Г |
Д |
|
(-∞; 1) |
(-∞;5] |
(-∞; 1) |
(1; 5] |
(-∞; 1 ) |
7. Розв’яжіть нерівність ![]() ≤ 1.
≤ 1.
|
А |
Б |
В |
Г |
Д |
|
(-∞; 0) |
(∞; 5] |
(-∞; 0) |
(0; 5] |
[5; +∞) |
8. Знайдіть область визначення функції у = ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
(1; 4) |
(-∞; 1) |
(-∞; 1) |
[1; 4] |
(1; 4] |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перегині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між раціональними рівняннями (1—4) та кількістю їхніх розв’язків (А—Д).
|
1 |
|
А |
жодного |
|
2 |
|
Б |
безліч |
|
3 |
|
В |
три |
|
4 |
|
Г |
один |
|
|
|
Д |
два |
Розв’яжіть завдання 10—12.
10. Розв’яжіть систему рівнянь 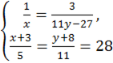 та запишіть у відповідь х0 + у0, де (х0; у0,) — розв’язок системи.
та запишіть у відповідь х0 + у0, де (х0; у0,) — розв’язок системи.
11. Розв’яжіть систему рівнянь 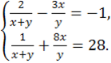 та запишіть у відповідь х0 + у0, де (х0; у0) — розв’язок системи.
та запишіть у відповідь х0 + у0, де (х0; у0) — розв’язок системи.
12. Укажіть найменше ціле число, яке є розв’язком нерівності ![]()
![]() 0.
0.
Алгебра. Тест до теми Числові послідовності. Арифметична і геометрична прогресії.
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Формулою n-го члена арифметичної прогресії 7, 9, 11, ... є
|
А |
Б |
В |
Г |
Д |
|
2n + 1 |
3n + 1 |
2n + 5 |
2n + 3 |
2n - 1 |
2. Знайдіть різницю арифметичної прогресії, якщо a1 = 7, a16 = 67.
|
А |
Б |
В |
Г |
Д |
|
-4 |
-2 |
2 |
4 |
5 |
3. Знайдіть суму перших десяти членів арифметичної прогресії, якщо а1 = 2, а2 = 5.
|
А |
Б |
В |
Г |
Д |
|
147 |
149 |
151 |
153 |
155 |
4. Знайдіть суму перших двадцяти непарних натуральних чисел.
|
А |
Б |
В |
Г |
Д |
|
410 |
400 |
220 |
210 |
200 |
5. Скільки додатних членів має арифметична прогресія 30, 26, 22,...?
|
А |
Б |
В |
Г |
Д |
|
5 |
6 |
7 |
8 |
10 |
6. Знайдіть перший від’ємний член арифметичної прогресії 102, 95, 88.......................................................
|
А |
Б |
В |
Г |
Д |
|
-3 |
-4 |
-5 |
-6 |
- 10 |
7. Знайдіть знаменник геометричної професії (bn), якщо b7 = - 4, b8 = 2.
|
А |
Б |
В |
Г |
Д |
|
-0,5 |
-2 |
-8 |
6 |
2 |
8. Дано геометричну прогресію (bn), перший член якої b1 = 32 і знаменник q = -![]() . Знайдіть b4.
. Знайдіть b4.
|
А |
Б |
В |
Г |
Д |
|
-4 |
4 |
-2 |
2 |
-1 |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між геометричною прогресією (1—4) та її знаменником (А—Д).
|
1 |
1; |
А |
-4 |
|
2 |
- |
Б |
|
|
3 |
-2; 8; -32; 128; … . |
В |
|
|
4 |
1; |
Г |
|
|
|
|
Д |
-12 |
Розв’яжіть завдання 10—12.
10. Число 96 є членом геометричної прогресії ![]() ,
, ![]() ,
, ![]() , … .
, … .
Знайдіть номер цього члена.
11. Чотири числа утворюють геометричну прогресію. Якщо з першого числа відняти 30, з другого 4, з третього 2, а з четвертого 8, то вийде арифметична прогресія. Знайдіть перший член геометричної прогресії.
12. Знайдіть суму ![]() +
+ ![]() +
+ ![]() + … +
+ … + ![]() .
.
Якщо знайдена сума — ціле число, то у відповідь запишіть це число, якщо знайдена сума — нескоротний звичайний дріб, то у відповідь запишіть суму чисельника і знаменника цього дробу.
Геометрія. Тест до теми Початкові поняття планіметрії. Геометрична фігура. Поняття про аксіоми і теореми, поняття про обернену теорему.
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильним. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Скільки всього відрізків позначено на рисунку?
|
А |
Б |
В |
Г |
Д |
|
4 |
8 |
6 |
10 |
12 |
2. Задано три точки А, В, С, причому АВ = 3 см, ВС = 4 см. АС = 5 см. Укажіть правильне твердження.
|
А |
Б |
В |
Г |
Д |
|
Точки А, В, С лежать на одній прямій. |
Точка В лежить між точками А і С. |
Точки А, В, С не лежать на одній прямій. |
Точка А лежить між точками В і С. |
Точка С лежить між точками А і В. |
3. Відрізок, довжина якого 50 см, розділений довільною точкою на два відрізки. Обчисліть відстань між серединами утворених відрізків.
|
А |
Б |
В |
Г |
Д |
|
10 см |
15 см |
30 см |
40 см |
25 см |
4. Відрізок, довжина якого 50 см, розділений трьома точками на чотири нерівні частини. Відстань між серединами крайніх частин — 30 см. Обчисліть відстань між серединами середніх частин відрізка
|
А |
Б |
В |
Г |
Д |
|
5 см |
10 см |
15 см |
20 см |
25 см |
5. Сума довжин двох відрізків дорівнює 12 см, а їх різниця — 2 см. Визначте довжину більшого відрізка.
|
А |
Б |
В |
Г |
Д |
|
3 см |
5 см |
7 см |
9 см |
10 см |
6. Відрізок довжиною а розділений натри рівні частини. Визначте, яку частину даного відрізка становить відстань між серединами першої і третьої утворених частин.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
7. Точки А, В,С лежать на одній прямій, АВ = 3 см, АС = 4 см. Якою є найменша відстань між точками В і С?
|
А |
Б |
В |
Г |
Д |
|
1 см |
3 см |
4 см |
7 см |
8 см |
8. Відрізок, довжина якого 50 см, розділений на три нерівні відрізки. Відстань між серединами крайніх відрізків дорівнює 30 см. Знайдіть довжину середнього відрізка
|
А |
В |
В |
Г |
Д |
|
5 см |
10 см |
15 см |
20 см |
25 см |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перегині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між поняттями (1—4) та їхніми значеннями (А—Д).
|
1 |
Середина відрізка |
А |
Частина прямої, яка складається з усіх точок цієї прямої, що лежать між двома даними її точками |
|
2 |
Півпряма або промінь |
Б |
Точка, що ділить даний відрізок на два рівних відрізки |
|
3 |
Доповняльні промені |
В |
Частина прямої, яка складається з усіх точок цієї прямої, що лежать по один бік від даної на ній точки |
|
4 |
Відрізок |
Г |
Будь-яка множина точок |
|
|
|
Д |
Різні півпрямі однієї й тієї самої прямої |
Розв’яжіть завдання 10—12.
10. Довжина відрізка АВ дорівнює 18 см. Точка С лежить між точками А і В. Знайдіть ВС (у см), якщо АС - ВС = 4 см.
11. Відрізок, довжина якого дорівнює 47 см, розділений на три нерівні відрізки. Відстань між серединами крайніх відрізків дорівнює 26 см. Знайдіть довжину середнього відрізка.
12. Дано шість точок, ніякі три із яких не лежать на одній прямій. Скільки всього можна провести прямих, яким належать кожні дві дані точки?
Геометрія. Тест до теми Кути та їх види
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Визначте кількість гострих кутів, зображених на рисунку.
|
А |
Б |
В |
Г |
Д |
|
3 |
5 |
6 |
7 |
8 |
2. Який кут утворюють стрілки годинника, коли показують 3 год?
|
А |
Б |
В |
Г |
Д |
|
гострий |
прямий |
тупий |
розгорнутий |
визначити неможливо |
3. Визначте величину кута, утвореного бісектрисами двох суміжних кутів.
|
А |
Б |
В |
Г |
Д |
|
30° |
90° |
120° |
180° |
135° |
4. Який кут є суміжним із кутом COD?
|
А |
Б |
В |
Г |
Д |
|
СОВ |
ВОА |
СОА |
BOD |
DOA |
5. Якщо один із суміжних кутів у 3 рази більше другого, то чому дорівнює більший кут?
|
А |
Б |
В |
Г |
Д |
|
45° |
180° |
135° |
90° |
120° |
6. Один із кутів, утворених при перетині двох прямих, удвічі менший суми трьох інших. Чому дорівнює найменший із цих кутів?
|
А |
Б |
В |
Г |
Д |
|
30° |
45° |
60° |
90° |
120° |
7. Бісектриса кута, величина якого 110°, з продовженням однієї з його сторін утворює кут. Визначте його градусну міру.
|
А |
Б |
В |
Г |
Д |
|
110° |
70° |
55° |
125° |
135° |
8. Різниця величин суміжних кутів дорівнює 20°. Визначте величину меншого кута.
|
А |
Б |
В |
Г |
Д |
|
30° |
70° |
80° |
90° |
60° |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перегині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між указаними кутами (1—4) та їх величинами (А—Д).
|
1 |
Кут між бісектрисами двох суміжних кутів |
А |
45° |
|
2 |
Кут між бісектрисами двох вертикальних кутів |
Б |
60° |
|
3 |
Кут між бісектрисою прямого кута і стороною цього кута |
В |
90° |
|
4 |
Кут між бісектрисою прямого кута і продовженням однією стороною цього кута |
Г |
135° |
|
|
|
Д |
180° |
Розв’яжіть завдання 10—12.
10. Кут між бісектрисою кута і продовженням однієї з його сторін дорівнює 135°. Знайдіть величину даного кута
11. Величина кута АВС дорівнює 140°. Промінь BD лежить між сторонами кута АВС. Знайдіть величину ∠ABD (у градусах), якщо ∠ABD: ∠DBC = 2 : 5.
12. Від прямої АВ в різних півплощинах відкладено ∠BAC = 30° і ∠BAD = 70°. Знайдіть ∠CAD.
Геометрія. Тест до теми Паралельні прямі і прямі, що перетинаються
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Укажіть правильне твердження.
|
А |
Б |
В |
Г |
Д |
|
До будь-якої прямої, можна провести лише одну пряму, перпендикулярну до даної |
Через точку поза прямої можна провести два перпендикуляри до даної прямої |
Через точку прямої можна провести лише одну пряму, перпендикулярну до даної прямої |
Через точку прямої не можна провести пряму, перпендикулярну до даної прямої |
Через точку поза прямої не можна провести прямої, яка паралельна даній прямій |
2. Розгляньте рисунок, на якому зображено дві прямі а і b, перетнуті прямою с. Як називаються кути 1 і 8?
|
А |
Б |
В |
Г |
Д |
|
внутрішні односторонні |
внутрішні різносторонні |
зовнішні односторонні |
зовнішні різносторонні |
відповідні |
3. На рисунку АВ ⊥ ВС, BD ⊥ АС. Яке із наведених тверджень правильне?
|
А |
Б |
В |
Г |
Д |
|
Відстань від точки А до прямої ВС дорівнює АС. |
Відстань від точки А до прямої BDдорівнює AD. |
Відстань від точки С до прямої АВ дорівнює АС. |
Відстань від точки В до прямої АС дорівнює ВС. |
Відстань від точки В до прямої АС дорівнює АВ. |
4. Різниця між величинами двох внутрішніх односторонніх кутів при паралельних прямих а і b та січній с дорівнює 40°. Обчисліть величину більшого з цих кутів.
|
А |
Б |
В |
Г |
Д |
|
70° |
100° |
110° |
120° |
90° |
- На рисунку паралельні прямі а і b перетнуто прямою с; ∠1 дорівнює 50°. Знайдіть величину ∠2.
|
А |
Б |
В |
Г |
Д |
|
30° |
40° |
50° |
60° |
90° |

6. На рисунку паралельні прямі а і b перетнуто прямою с; ∠1 дорівнює 50°. Знайдіть величину ∠3.
|
А |
Б |
В |
Г |
Д |
|
120° |
130° |
140° |
150° |
160° |

7. Дві прямі перетинаються і утворюють чотири кути. Різниця двох утворених кутів дорівнює 60°. Знайдіть гострий кут між прямими.
|
А |
Б |
В |
Г |
Д |
|
30° |
45° |
50° |
60° |
75° |
8. Через вершину кута 40° проведено прямі, перпендикулярні до його сторін. Обчисліть величину меншого з кутів, утворених при перетині цих перпендикулярних прямих.
|
А |
Б |
В |
Г |
Д |
|
80° |
90° |
140° |
40° |
20° |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між поняттями (1—1) та їх означеннями (А—Д).
|
1 |
Перпендикулярні прямі |
А |
Довжина перпендикуляра. проведеного з даної точки до прямої |
|
2 |
Перпендикуляр до даної прямої, проведений з даної точки |
Б |
Прямі, які перетинаються під прямим кутом |
|
3 |
Паралельні прямі |
В |
Відрізок прямої, перпендикулярної до даної прямої, який має одним із своїх кінців точку їх перетину, а другим кінцем —дану точку |
|
4 |
Відстань від точки до прямої |
Г |
Дві прямі, які перетинаються |
|
|
|
Д |
Дві прямі, які не перетинаються |
Розв'яжіть завдання 10—12.
10. Паралельні прямі а і b перетнуто прямою с. Сума двох із утворених восьми кутів дорівнює 30°. Знайдіть тупий кут між прямими а і с.
11. Паралельні прямі а і b перетнуто прямою с. Різниця двох із утворених восьми кутів дорівнює 30°. Знайдіть гострий кут між прямими а і с.
12. Паралельні прямі а і b перетнуто прямою с. Різниця двох із утворених восьми кутів дорівнює 30°. Знайдіть тупий кут між прямими а і с.
Геометрія. Тест до теми Трикутники та їх види.
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. На рисунку зображено трикутник ABC, периметр якого дорівнює 24 см, периметр трикутника ABD — 12 см, а периметр трикутника BCD — 20 см. Знайдіть BD.
|
А |
Б |
В |
Г |
Д |
|
10 см |
8 см |
4 см |
12 см |
5 см |
2. На рисунку ВС = AD, ∠1 = ∠2. Яке твердження правильне?
|
А |
Б |
В |
Г |
Д |
|
∆АВС = ∆CDA |
∆АВС ≠ ∆ADC |
АВ ≠ CD |
∠4 = ∠1 |
∠3 = ∠2 |
![]()
3. На рисунку ОА = OD, ОВ = ОС. Яке з наведених тверджень правильне?
|
А |
Б |
В |
Г |
Д |
|
∆АОВ ≠ ∆DOC |
∆ADC = ∆АСВ |
∠1 = ∠2 |
AB = CD |
AD = ВС |
![]()
4. У рівнобедреному трикутнику ABC з основою ВС проведено бісектриси BL1 і CL2 Яке з тверджень правильне?
|
А |
Б |
В |
Г |
Д |
|
CL1 = AL1 |
ВL2 = AL2 |
CL2 = BL1 |
CL1 ⊥ BL1 |
CL2 ⊥ B2 |
5. На рисунку зображено відрізки АВ і CD, що перетинаються в точці F, яка є серединою кожного з них. Яке твердження правильне?
|
А |
Б |
В |
Г |
Д |
|
∆AFC = ∆BFD |
∆AFD = ∆BFD |
∠FDB = ∠FCB |
ВС ≠ AD |
АВ = CD |
6. У трикутнику ABC ∠DAC = ∠DCA, АВ = 4 см, АС = 3 см. Периметр трикутника АВD дорівнює 9 см. Знайдіть периметр трикутника AВС.
|
А |
Б |
В |
Г |
Д |
|
10 см |
15 см |
17 см |
12 см |
10 см |
7. На рисунку АВ = АС, ∠1 = ∠2. Яке з наведених тверджень правильне?
|
А |
Б |
В |
Г |
Д |
|
∆АВО ≠ ∆ACD |
∆ABD = ∆BCD |
ВО ≠ ОС |
AD ⊥ BC |
АD = BD |
8. У рівнобедреному трикутнику АВС з основою ВС проведено висоти ВН1, і СН2. Яке з поданих тверджень правильне?
|
А |
Б |
В |
Г |
Д |
|
ВН1⊥ СН2 |
ВН1 = СН2 |
ВН1 = АН1 |
СН2 = АН2 |
ВН2 = АН2 |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перегині відповідних рядків (цифри) і колонок (букви).
9. Утворіть правильні твердження, об’єднавши їх початок (1—4) та кінець (А—Д).
|
1 |
Якщо у трикутника лише дві медіани рівні, то цей трикутник |
А |
тупокутний |
|
2 |
Якщо у трикутника одна медіана дорівнює половині сторони, до якої вона проведена, то цей трикутник |
Б |
рівнобедрений, відмінний від рівностороннього |
|
3 |
Якщо у трикутника три медіани рівні, то цей трикутник |
В |
прямокутний |
|
4 |
Якщо точка перегину висот трикутника лежить поза ним, то це трикутник |
Г |
рівносторонній |
|
|
|
Д |
гострокутний, відмінний від рівностороннього |
Розв'яжіть завдання 10—12.
10. Знайдіть основу рівнобедреного трикутника (у см). якщо його периметр дорівнює 26 см, причому бічна сторона на 4 см більша за основу.
11. Знайдіть основу рівнобедреного трикутника (у см), периметр якого дорівнює 20 см, а бічна сторона вдвічі більша основи.
12. Знайдіть бічну сторону рівнобедреного трикутника (у см), периметр якого дорівнює 18 см, а бічна сторона на 6 см більша основи.
Геометрія. Тест до теми Сума кутів трикутника
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильним. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. У трикутнику ABC проведено бісектриси ВМ і CN, які перетинаються в точці К. Знайдіть кут ВКС, якщо ∠A = 120°.
|
А |
Б |
В |
Г |
Д |
|
|
140° |
|
160° |
120° |
2. На рисунку ∠NBM= 40°, ∠LCB = 100°. Знайдіть ∠LAF.
|
А |
Б |
В |
Г |
Д |
|
100° |
110° |
120° |
130° |
140° |
3. У трикутнику ABC ∠A = 80°, ∠C = 40°. Висоти АЕ і CD перетинаються в точці К. Знайдіть ∠АКС.
|
А |
Б |
В |
Г |
Д |
|
110° |
120° |
130° |
140° |
160° |
4. Усередині трикутника ABC взято точку Отак, що ∠ADC = 140°, ∠BAD = 35°, ∠BCD = 40°. Знайдіть ∠ABC.
|
А |
Б |
В |
Г |
Д |
|
35° |
45° |
55° |
65° |
75° |
5. Кут між бісектрисою і висотою прямокутного трикутника, які проведені з вершини прямого кута, дорівнює 25°. Знайдіть більший гострий кут трикутника.
|
А |
б |
В |
Г |
Д |
|
45° |
50° |
60° |
70° |
80° |
6. Знайдіть кут між бічними сторонами рівнобедреного трикутника, якщо кут при його основі дорівнює 50°.
|
А |
Б |
В |
Г |
Д |
|
45° |
50° |
60° |
70° |
80° |
7. Бісектриси трикутника ABC. проведені з вершин А і С, перегинаються в точці D. Знайдіть ∠ADC, якщо ∠A = 70°, ∠C = 80°.
|
А |
Б |
В |
Г |
Д |
|
100° |
105° |
110° |
115° |
120° |
8. Знайдіть величину кута х, зображеного на рисунку.
|
А |
Б |
В |
Г |
Д |
|
95° |
120° |
140° |
150° |
160° |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між трикутниками (1—4) та їх кутами (А—Д).
|
1 |
Трикутник, у якого зовнішні кути пропорційні числам 3, 4, 5 |
А |
36°, 54°, 90° |
|
2 |
Трикутник, у якого кути пропорційні числам 2, 3, 5 |
Б |
20°, 40°, 120° |
|
3 |
Трикутник, у якого один із його кутів утричі менший другого і вп’ятеро менший третього |
В |
40°, 50°, 90° |
|
4 |
Трикутник, кути якого пропорційні числам 1, 2, 6 |
Г |
20°, 60°, 100° |
|
|
|
Д |
30°, 60°, 90° |
Розв’яжіть завдання 10—12.
10. У трикутнику АВС проведені висоти АЕ і CD, що перетинаються в точці О. Знайдіть кут АОС, якщо ∠B = 60°.
11. У трикутнику ABC: ∠A = 42°, ∠B = 64°. Із вершин кутів А і С проведені бісектриси трикутника, що перетинаються в точці О. Знайдіть градусну міру кута АОС.
12. У рівнобедреному трикутнику ABC (АВ — основа) ∠A = 32°. Знайдіть ∠C.
Геометрія. Тест до теми Подібність трикутників. Теорема Піфагора.
Завдання 1—8 мають по п’яте варіантів відповіді, серед яких лише один правильний. Виберіть правильну на Вашу думку, відповідь і позначте її у бланку А.
1. Сторони прямокутника дорівнюють 6 см і 8 см. Знайдіть його діагональ (у см).
|
А |
Б |
В |
Г |
Д |
|
5 см |
7 см |
10 см |
14 см |
15 см |
2. Сторони трикутника дорівнюють 10 см, 15 см і 20 см. Знайдіть найбільшу сторону подібного йому трикутника, периметр якого дорівнює 90 см.
|
А |
Б |
В |
Г |
Д |
|
20 см |
30 см |
40 см |
50 см |
60 см |
3. У трикутнику АВС (див. рисунок) ∠B = 90°, BD ⊥ АС. Яке твердження правильне?
|
А |
Б |
В |
Г |
Д |
|
∠BAD = ∠ABD |
∠АО ≠ ∠DBC |
∆ABD неподібний ∆BCD |
∆ABD ~ ∆АСВ |
∆ABD неподібний ∆АСВ |
4. У трикутнику ABC АВ = а, АС = b. MF || АС, MF = c. Знайдіть AM.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
5. Знайдіть висоту рівностороннього трикутника, якщо його сторона дорівнює а.
|
A |
Б |
В |
Г |
Д |
|
|
|
|
|
|
6. Знайдіть сторону рівностороннього трикутника, якщо його медіана дорівнює m.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
7. Сторони трикутника дорівнюють 13 см, 14 см і 15 см. Знайдіть висоту трикутника, проведену до сторони, яка дорівнює 14 см.
|
А |
Б |
В |
Г |
Д |
|
11 см |
11 |
12 см |
12 |
13 см |
8. Якщо катети прямокутного трикутника дорівнюють а і Ь, то медіана, проведена до гіпотенузи, дорівнює
|
A |
Б |
В |
Г |
Д |
|
|
|
|
|
|
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між умовами задач (1—4) та їх відповідями (А—Д).
|
1 |
Катети прямокутного трикутника дорівнюють 6 см і 8 см. Знайдіть гіпотенузу |
А |
3 см |
|
2 |
Знайдіть катет прямокутного трикутника, якщо дві інші його сторони дорівнюють 4 см і 5 см |
Б |
4 см |
|
3 |
Знайдіть висоту рівнобедреного трикутника, проведену до основи, якщо основа дорівнює 6 см, а бічна сторона — 5 см |
В |
6 см |
|
4 |
Похила, довжина якої дорівнює 10 см, має проекцію 8 см. Знайдіть довжину перпендикуляра |
Г |
8 см |
|
|
|
Д |
10 см |
Розв’яжіть завдання 10—12.
10. Основа рівнобедреного трикутника дорівнює 70 см, а проведена до неї висота — 12 см. Знайдіть периметр трикутника
11. У сонячний день довжина тіні від дерева становить 16 м. У той самий час тінь від хлопчика який має зріст 1,5 м, дорівнює 2 м (див. рисунок). Визначте висоту дерева

12. У трикутнику ABC АВ = 4 см. Точка D належить стороні ВС, причому BD = 1 см, DC = 15 см, AD = 3,5 см. Знайдіть довжину сторони АС (у см).
Геометрія. Тест до теми Поняття площі. Площа трикутника
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Знайдіть площу трикутника, зображеного на рисунку, якщо площа 1 клітинки — 1 см2.
|
А |
Б |
В |
Г |
Д |
|
5 см2 |
6 см2 |
7 см2 |
8 см2 |
9 см2 |
2. Сторони трикутника дорівнюють 9 см, 10 см, 17 см. Знайдіть його площу (у см2).
|
А |
Б |
В |
Г |
Д |
|
36 см2 |
38 см2 |
40 см2 |
42 см2 |
45 см2 |
3. Знайдіть площу трикутника, сторони якого дорівнюють 7 см; 15 см; 20 см.
|
А |
Б |
В |
Г |
Д |
|
22 см2 |
32 см2 |
42 см2 |
52 см2 |
62 см2 |
4. Знайдіть площу прямокутного трикутника, у якого гіпотенуза дорівнює 17 см, а один із катетів — 15 см.
|
А |
Б |
В |
Г |
Д |
|
255 см2 |
127,5 см2 |
136 см2 |
120 см2 |
60 см2 |
5. Точка М — середина сторони квадрата ABCD (див. рисунок). Площа зафарбованої частини дорівнює 7 см2. Знайдіть площу всього квадрата (у см2).
|
А |
В |
В |
Г |
Д |
|
14 см2 |
21 см2 |
28 см2 |
35 см2 |
42 см2 |
6. У квадраті ABCD точка Е — середина сторони CD. Знайдіть відношення заштрихованої області до площі квадрата
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
7. Знайдіть площу прямокутного трикутника (у см2), якщо радіус кола описаного навколо нього, дорівнює 5 см, а один із катетів — 6 см.
|
А |
Б |
В |
Г |
Д |
|
15 см2 |
24 см2 |
30 см2 |
48 см2 |
60 см2 |
8. Знайдіть площу прямокутного трикутника (у см2), якщо його катети дорівнюють 3 см і 4 см.
|
А |
Б |
В |
Г |
Д |
|
5 см2 |
6 см2 |
7 см2 |
8 см2 |
12 см2 |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між задачами (1—4) та їх відповідями (А—Д).
|
1 |
Знайдіть бічну сторону рівнобедреного трикутника, якщо його основа дорівнює 18, а площа трикутника — 108. |
А |
4.8 |
|
2 |
Знайдіть висоту трикутника, яка проведена до сторони, що дорівнює 6, якщо висота цього трикутника, проведена до сторони 8. дорівнює 9. |
Б |
12 |
|
3 |
Знайдіть площу рівнобедреного трикутника, якщо його основа дорівнює 16, а бічна сторона — 10. |
В |
36 |
|
4 |
Знайдіть висоту прямокутного трикутника, проведену до гіпотенузи, якщо катети трикутника дорівнюють 6 і 8. |
Г |
48 |
|
|
|
Д |
15 |
Розв'яжіть завдання 10—12.
10. Периметр прямокутного трикутника дорівнює 60 см. Висота, проведена до гіпотенузи, дорівнює 12 см. Знайдіть площу трикутника (у см2).
11. Гіпотенуза прямокутного трикутника дорівнює 13 см, а один із катетів — 5 см. Знайдіть площу цього трикутника (у см2).
12. Знайдіть площу прямокутного трикутника, якщо його висота ділить гіпотенузу на відрізки 18 см і 32 см (у см2).
Геометрія. Тест до теми Коло, круг. Дотична до кола.
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну. на Вашу думку, відповідь і позначте її у бланку А.
1. З однієї точки кола проведено дві взаємно перпендикулярні хорди, які віддалені від центра на 3 см і 5 см відповідно. Знайдіть довжину більшої хорди.
|
А |
Б |
В |
Г |
Д |
|
3 см |
5 см |
8 см |
10 см |
12 см |
2. Скільки всього кіл можна провести через дві різні точки?
|
А |
Б |
В |
Г |
Д |
|
одне |
два |
три |
жодного |
безліч |
3. Як розміщені кола з діаметрами 10 см і 6 см, якщо відстань між їх центрами дорівнює 8 см?
|
А |
Б |
В |
Г |
Д |
|
перетинаються |
мають зовнішній дотик |
не мають спільних точок |
мають внутрішній дотик |
збігаються |
4. Дано три кола з центрами О1, О2, О3 і радіусами відповідно 1 см, 3 см, 5 см, які мають зовнішній дотик. Знайдіть периметр трикутника О1О2О3 (у см).
|
А |
Б |
В |
Г |
Д |
|
9 см |
18 см |
24 см |
27 см |
36 см |
5. Радіус кола дорівнює R. Із точки, яка віддалена від центра кола на відстань 2R, проведено дотичні до кола. Знайдіть кут між дотичними (у градусах).
|
А |
Б |
В |
Г |
Д |
|
30° |
75° |
45° |
90° |
60° |
6. Скільки всього кіл можна провести через три дані точки, що не лежать, на одній прямій?
|
А |
Б |
В |
Г |
Д |
|
одне |
два |
три |
жодного |
безліч |
7. Із даної точки кола проведено діаметр і хорду, яка дорівнює радіусу. Знайдіть кут між діаметром і хордою.
|
А |
Б |
В |
Г |
Д |
|
30° |
60° |
45° |
80° |
90° |
8. Радіус кола дорівнює R. Із точки, яка віддалена від центра на відстань 2R, проведено дотичні до кола. Знайдіть довжини дотичних.
|
А |
Б |
В |
Г |
Д |
|
R |
R |
R |
2R |
|
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перегині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між інформацією щодо радіусів двох кіл і відстаней між їх центрами (1—4) та взаємним розташуванням цих кіл (рис. А—Д).
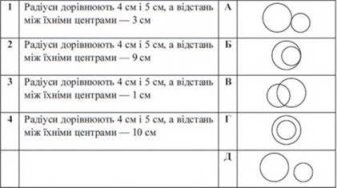
Розв'яжіть завдання 10—12.
10. АВ і АС — дотичні, В і С — точки дотику. Знайдіть ВАС (у градусах), якщо ВОС = 110°.
11. Через точки В, С, D кола з центром О проведено три дотичні АВ, АС і FK, які перетинаються в точках A, F, К. Знайдіть периметр (у см) трикутника AFK, якщо АВ + АС = 20 см.
12. Два кола з радіусами 4 см і 9 см дотикаються зовні. Знайдіть відстань між точкам и дотику спільної дотичної до даних кіл (у см).
Геометрія. Тест до теми Вписані кути.
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. На рисунку центральний кут дорівнює 120°. Знайдіть градусну міру вписаного кута, який опирається на ту саму дугу.
|
А |
Б |
В |
Г |
Д |
|
30° |
40° |
60° |
120° |
180° |
2. На рисунку ∠ACB = 80°. Знайдіть градусну міру кута АОВ.
|
А |
Б |
В |
Г |
Д |
|
80° |
90° |
100° |
120° |
160° |
3. Центральний кут на 20° більше вписаного кута, який опирається на ту ж дугу. Знайдіть градусну міру центрального кута.
|
А |
Б |
В |
Г |
Д |
|
20° |
30° |
40° |
45° |
50° |
4. Пряма а дотикається до кола в точці В. Знайдіть ∠AOB (у градусах), якщо ∠ABC = 50°.
|
А |
Б |
В |
Г |
Д |
|
100° |
101° |
102° |
103° |
104° |
5. АВ — діаметр, АС — хорда. Знайдіть ∠BOA (у градусах), якщо ∠ACO = 52°.
|
А |
Б |
В |
Г |
Д |
|
100° |
101° |
102° |
103° |
104° |
6. На рисунку ∠AFC = 30°. Знайдіть градусну міру кута DBC.
|
А |
Б |
В |
Г |
Д |
|
90° |
100° |
105° |
120° |
150° |
7. До кола з центром у точці О проведено дотичну АВ (В — точка дотику ). ВС - хорда, що утворює з радіусом кола кут 35° (див. рисунок). Знайдіть градусну міру кута ABC.
|
А |
Б |
В |
Г |
Д |
|
35° |
45° |
55° |
65° |
70° |
8. На рисунку ∠BAC = 30°. Знайдіть градусну міру кута AFC.
|
А |
Б |
В |
Г |
Д |
|
30° |
45° |
90° |
50° |
60° |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перегині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між задачами (1—4) та їх відповідями (А—Д).
|
1 |
Знайдіть центральний кут, який спирається на дуту, що становить |
А |
50° |
|
2 |
Знайдіть вписаний кут, який спирається на дугу, що становить |
Б |
75° |
|
3 |
Знайдіть центральний кут, який спирається на дугу, що становить |
В |
100° |
|
4 |
Знайдіть вписаний кут, який спирається на дугу, що становить |
Г |
140 |
|
|
|
Д |
150° |
Розв’яжіть завдання 10—12.
10. Центральний кут на 35° більший за вписаний кут, що спирається на ту саму дугу, що і центральний. Знайдіть градусну міру центрального кута.
11. Вписаний кут на 20° менший за центральний кут, який спирається на ту саму дугу, що і вписаний. Знайдіть градусну міру вписаного кута.
12. Один із гострих кутів прямокутного трикутника дорівнює 35°. Під яким кутом (у градусах) видно катет, протилежний до даного гострого кута, із центра описанного кола?
Геометрія. Тест до теми Довжина кола і площа круга.
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Знайдіть довжину кола (у см), якщо його радіус дорівнює 2 см.
|
А |
Б |
В |
Г |
Д |
|
|
4 |
4 |
2 |
2 |
2. Довжина відрізка АВ дорівнює а. На ньому позначено точки С1, С2, С3, ... Сn і побудовано півкола, які мають діаметри АС1, С1С2, С2С3 ... СnВ. Знайдіть довжину побудованої кривої з кінцями в точках А і В.
![]()
|
А |
Б |
В |
Г |
Д |
|
3 |
|
|
2 |
3 |
3. Точки А і В лежать на колі, хорда АВ не проходить через його центр. Порівняйте довжину кола С і 16![]() , якщо довжина хорди АВ дорівнює 16.
, якщо довжина хорди АВ дорівнює 16.
4. Сторона квадрата дорівнює а, із його вершин побудовано дуги кіл радіусом ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
С = 16 |
С < 16 |
С > 16 |
порівняти не можна |
С >16 |
Знайдіть площу заштрихованої фігури.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
а2 |

5. Обчисліть площу кругового кільця (у см2), якщо його внутрішній і зовнішній діаметри дорівнюють 6 см і 8 см відповідно.
|
А |
Б |
В |
Г |
Д |
|
6 |
7 |
8 |
12 |
24 |
6. Знайдіть довжину дуги кола радіуса 120 см, якщо її кутова величина дорівнює 30°.
|
А |
Б |
В |
Г |
Д |
|
5 |
10 |
15 |
20 |
24 |
7. Три рівні кола радіусом R дотикаються одне одного. Знайдіть площу заштрихованого криволінійного трикутника.
|
А |
Б |
В |
Г |
Д |
|
( |
( |
( |
( |
R2 |
8. Два рівні круга радіусом r розміщені всередині круга (див. рисунок), радіус якого більший за r, і дотикаються до нього. Знайдіть площу заштрихованої області, якщо круги меншого радіуса дотикаються один до одного в точці О — центрі великого круга
|
A |
Б |
В |
Г |
Д |
|
|
|
|
2 |
r2 |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між задачами (1 —4) та їх відповідями (А—Д).
|
1 |
Знайдіть площу круга, якщо довжина кола, що обмежує його, дорівнює 6 |
А |
4 |
|
2 |
Знайдіть площу кругового сектора радіуса 10, центральний кут якого дорівнює 36° |
Б |
3 |
|
3 |
Знайдіть довжину кола, що обмежує круг, площа якого дорівнює 9 |
В |
6 |
|
4 |
Знайдіть довжину дуги кола радіуса 3, яка становить |
Г |
9 |
|
|
|
Д |
10 |
Розв’яжіть завдання 10—12.
10. Знайдіть S площу заштрихованої фігури за рисунком (у см2). У відповідь запишіть ![]()
11. Знайдіть відношення площі круга, описаного навколо квадрата, до площі круга, вписаного в нього.

12. Знайдіть площу S кругового кільця (у см2), обмеженого двома колами з одним і тим самим центром і радіусами, що дорівнюють 4 см і 6 см. У відповідь запишіть ![]() .
.
Геометрія. Тест до теми Вписані і описані трикутники.
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Якщо коло, вписане в трикутник ABC, дотикається до його сторін у точках A1, В1, С1, то
|
А |
Б |
В |
Г |
Д |
|
2 АС1 = АС + ВС - АВ |
2АС1 = АВ + ВС - АС |
2АС= АВ +АС - ВС |
2АС1 = АВ - ВС |
2АС1 =АВ + АС + ВС |
2. Якщо коло дотикається до гіпотенузи і продовження катетів прямокутного трикутника (див. рисунок), то його діаметр дорівнює
|
А |
Б |
В |
Г |
Д |
|
гіпотенузі |
Сумі катетів |
півпериметру трикутника |
Периметру трикутника |
різниці гіпотенузи і меншого катета |
3. Знайдіть радіус кола (у см2), описаного навколо рівностороннього трикутника, якщо сторона трикутника дорівнює 2![]() см.
см.
|
А |
Б |
В |
Г |
Д |
|
1 см |
|
2 см |
3 см |
4 см |
4. Знайдіть радіус кола (у см2), описаного навколо прямокутного рівнобедреного трикутника з гіпотенузою 10 см.
|
А |
Б |
В |
Г |
Д |
|
1 см |
2 см |
3 см |
4 см |
5 см |
5. Знайдіть діаметр кола (у см2), описаного навколо трикутника зі сторонами 8 см, 15 см, 17 см.
|
А |
Б |
В |
Г |
Д |
|
8 см |
10 см |
15 см |
17 см |
19 см |
6. Знайдіть діаметр кола (у см), вписаного в трикутник, сторони якого дорівнюють 15 см, 13 см, 4 см.
|
А |
В |
В |
Г |
Д |
|
2 см |
3 см |
4 см |
6 см |
8 см |
7. Катети прямокутного трикутника дорівнюють 6 см і 8 см. Знайдіть радіус кола (у см), вписаного в трикутник.
|
А |
Б |
В |
Г |
Д |
|
1 см |
2 см |
3 см |
4 см |
5 см |
8. Бічна сторона рівнобедреного трикутника дорівнює 6 см, а висота, проведена до основи, дорівнює 4 см. Знайдіть діаметр кола, описаного навколо трикутника (у см).
|
А |
Б |
В |
Г |
Д |
|
7 см |
8 см |
9 см |
10 см |
12 см |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. У кожному реченні (1—4) доберіть закінчення (А—Д) так, щоб утворилося правильне твердження щодо властивостей трикутника.
|
1 |
Якщо в трикутнику центр описаного кола збігаєтеся з центром уписаного кола, то такий трикутник |
А |
рівнобедрений, але не рівносторонній і не тупокутний |
|
2 |
Якщо в трикутнику одна із медіан є радіусом описаного кола, то такий трикутник |
Б |
рівнобедрений, тупокутний |
|
3 |
Якщо центр уписаного кола лежить на одній із медіан, а центр описаного кола лежить на продовженні цієї медіани, то такий трикутник |
В |
довільний тупокутний |
|
4 |
Якщо в трикутнику центри описаного і вписаного кіл лежать на одній із медіан і не збігаються, то такий трикутник |
Г |
рівносторонній |
|
|
|
Д |
прямокутний |
Розв’яжіть завдання 10—12.
10. Периметр рівностороннього трикутника дорівнює 12 ![]() см. Знайдіть радіус кола (у см), вписаного в цей трикутник.
см. Знайдіть радіус кола (у см), вписаного в цей трикутник.
11. Периметр рівностороннього трикутника дорівнює 15 ![]() см. Знайдіть радіус кола (у см), описаного навколо цього трикутника.
см. Знайдіть радіус кола (у см), описаного навколо цього трикутника.
12. Гіпотенуза і катет прямокутного трикутника відносяться як 5 : 4, а другий катет дорівнює 12 см. Знайдіть радіус кола (у см), вписаного в цей трикутник.
Геометрія. Тест до теми Тригонометричні функції гострого кута прямокутного трикутника.
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Користуючись рисунком, знайдіть cos А.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
1 |
2. Катети прямокутного трикутника дорівнюють 6 см і 8 см. Знайдіть тангенс куга прилеглого до меншого катета.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
3. Катети прямокутного трикутника дорівнюють 8 см і 15 см. Знайдіть синус кута, протилежного більшому катету.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
4. Знайдіть tg 30°.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
2 |
5. Знайдіть значення виразу 2sin 60°.
|
А |
Б |
В |
Г |
Д |
|
1 |
2 |
|
|
2 |
6. У прямокутному трикутнику ABC (∠A = 90°) ВС = 4 см, ∠B = β. Знайдіть АС.
|
А |
Б |
В |
Г |
Д |
|
4sin |
4cos β |
4tg β |
|
|
7. У прямокутному трикутнику ABC (∠B = 90°) ВС= 10 см, ∠A = а. Знайдіть АВ.
|
А |
Б |
В |
Г |
Д |
|
|
|
10tga |
|
10sina |
8. У прямокутному трикутнику ABC (∠B = 90°) ВС = 2 CM, ∠C = γ. Знайдіть АС.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
2tgγ |
2cosγ |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між виразом (1—4) та його числовим значенням (А—Д).
|
1 |
sin30° + tg45° |
Ф |
1 - |
|
2 |
|
Б |
0 |
|
3 |
|
В |
1 |
|
4 |
2sin60°- tg60° |
Г |
1 |
|
|
|
Д |
|
Розв'яжіть завдання 10—12.
10. Діагональ прямокутника дорівнює 12 см і утворює зі стороною кут 30°. Знайдіть периметр прямокутника (у см). Ураховуйте, що ![]() ≈ 1,7. Відповідь округліть до цілих.
≈ 1,7. Відповідь округліть до цілих.
11. Більша діагональ ромба дорівнює 3 ![]() , а гострий кут ромба дорівнює 60°. Знайдіть сторону ромба.
, а гострий кут ромба дорівнює 60°. Знайдіть сторону ромба.
12. Катет прямокутного трикутника дорівнює 9![]() см, а прилеглий до нього кут — 60°. Знайдіть довжину (у см) бісектриси трикутника, проведеної з вершини цього кута.
см, а прилеглий до нього кут — 60°. Знайдіть довжину (у см) бісектриси трикутника, проведеної з вершини цього кута.
Геометрія. Тест до теми Розв’язування довільних трикутників
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Дві сторони трикутника дорівнюють V3 см і 1 см, а кут між ними — 30°. Знайдіть третю сторону трикутника.
|
А |
Б |
В |
Г |
Д |
|
1 см |
|
|
2 см |
3 см |
2. Виміряти відстань безпосередньо між точками А і В перешкоджає ставок. Для знаходження відстані АВ виміряли відстані від точок А і В до певної точки С та кут АСВ. Обчисліть відстань АВ. якщо були одержані такі результати вимірювань: АС = 30м, ВС = 50 м, ∠ACB = 120°.
|
А |
Б |
В |
Г |
Д |
|
90 м |
85 м |
80 м |
75 м |
70 м |
![]()
3. Сторони трикутника дорівнюють 1 см, 3 ![]() см і 5 см. Знайдіть найбільший кут трикутника
см і 5 см. Знайдіть найбільший кут трикутника
|
А |
Б |
В |
Г |
Д |
|
90° |
120° |
135° |
150° |
175° |
4. Сторони трикутника, одна з яких удвічі більша за другу, утворюють 120°, а довжина третьої сторони дорівнює 3 ![]() . Знайдіть найменшу сторону трикутника.
. Знайдіть найменшу сторону трикутника.
|
А |
Б |
В |
Г |
Д |
|
1 |
2 |
3 |
4 |
5 |
5. Сторона трикутника дорівнює 20 см, а протилежний кут — 150°. Знайдіть радіус кола, описаного навколо трикутника.
|
А |
Б |
В |
Г |
Д |
|
30 см |
25 см |
20 см |
15 см |
10 см |
6. Два кути трикутника дорівнюють 30° і 45°. Знайдіть сторону, протилежну куту 30°, якщо сторона, протилежна куту 45°, дорівнює ![]() см.
см.
|
А |
Б |
В |
Г |
Д |
|
1 см |
2 см |
3 см |
|
2 |
7. У рівнобедреному трикутнику основа дорівнює я, а кут при основі — 26- Знайдіть бісектрису, проведену до бічної сторони.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
8. Якщо кути трикутника відносяться як 1 : 2 : 3, то відношення відповідних сторін трикутника є таким
|
А |
Б |
В |
Г |
Д |
|
1 : 2 : 3 |
1 : |
1 : 2 : |
1 : |
1 : |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перегині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між виразом (1—4) та його числовим значенням (А—Д).
|
1 |
sin 135° |
А |
- |
|
2 |
cos 135° |
Б |
|
|
3 |
cos 150° |
В |
- |
|
4 |
cos 180° |
Г |
0 |
|
|
|
Д |
-1 |
Розв’яжіть завдання 10—12.
10. Дві сторони трикутника дорівнюють ![]() см і 1 см, а кут між ними становить 135°. Знайдіть третю сторону (у см).
см і 1 см, а кут між ними становить 135°. Знайдіть третю сторону (у см).
11. Сторони трикутника дорівнюють 4![]() см, 7 см, 5 см. Знайдіть кут (у градусах), який лежить проти найменшої сторони.
см, 7 см, 5 см. Знайдіть кут (у градусах), який лежить проти найменшої сторони.
12. Дві сторони трикутника дорівнюють 7 см і 11 см, а медіана, проведена до третьої сторони, дорівнює 6 см. Знайдіть третю сторону (у см).
Геометрія. Тест до теми Паралелограми, їх види та властивості
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Діагональ паралелограма утворює з двома його сторонами кути 15° і 45°. Знайдіть більший кут паралелограма (у градусах).
|
А |
Б |
В |
Г |
Д |
|
60° |
90° |
120° |
135° |
150° |
2. Знайдіть менший кут паралелограма, якщо сума двох кутів паралелограма дорівнює 120°.
|
А |
Б |
В |
Г |
Д |
|
15° |
30° |
45° |
60° |
90° |
3. Чотирикутник ABCD — паралелограм. Відомо, що АВ = 2 см, ВС = 4 см, ∆А = 60°. Знайдіть діагональ АС.
|
А |
Б |
В |
Г |
Д |
|
6 см |
2 |
2 |
10 см |
2 |
4. У коло, діаметр якого дорівнює ![]() , вписано чотирикутник ABCD. Знайдіть діагональ BD, якщо ∠BAD = 30°.
, вписано чотирикутник ABCD. Знайдіть діагональ BD, якщо ∠BAD = 30°.
|
А |
Б |
В |
Г |
Д |
|
3 |
2 |
4 |
|
2 |
5. У паралелограмі ABCD АВ = 32, AD= 14, BD = 42. Знайдіть АС (у см).
|
А |
Б |
В |
Г |
Д |
|
22 |
24 |
26 |
28 |
30 |
6. Чотирикутник ABCD — паралелограм. Точка К — середина сторони АВ. Відрізок DK перетинає діагональ АС у точці О. Знайдіть відношення довжин відрізків AО : ОС.
|
А |
Б |
В |
Г |
Д |
|
1 : 2 |
1 : 3 |
2 : 3 |
3 : 4 |
3 : 5 |
![]()
7. Знайдіть менший кут паралелограма, якщо різниця двох кутів паралелограма дорівнює 120°.
|
А |
Б |
В |
Г |
Д |
|
15° |
30° |
45° |
60° |
90° |
. У паралелограмі ABCD АС = 13, AD = 7, BD = 21. Знайдіть АВ.
|
А |
Б |
В |
Г |
Д |
|
10 |
13 |
14 |
16 |
18 |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Доберіть до кожного початку речення (1—4) його закінчення (А—Д) так, щоб утворилося правильне твердження.
|
1 |
Середини сторін довільною паралелограма є |
А |
вершинами квадрата |
|
2 |
Середини сторін довільного прямокутника є |
В |
вершинами ромба |
|
3 |
Середини сторін довільного ромба є |
В |
вершинами прямокутника |
|
4 |
Середини сторін довільного квадрата є |
Г |
вершинами паралелограма |
|
|
|
Д |
вершинами трапеції |
Розв’яжіть завдання 10—12.
10. Діагоналі паралелограма дорівнюють 17 см і 19 см, а сторони відносяться як 2:3. Знайдіть периметр паралелограма (у см).
11. Діагоналі паралелограма дорівнюють 6![]() см і 2 см, а кут між ними 45°. Знайдіть більшу сторону паралелограма (у см).
см і 2 см, а кут між ними 45°. Знайдіть більшу сторону паралелограма (у см).
12. Діагоналі ромба дорівнюють 12 см і 12![]() см. Знайдіть гострий кут ромба (у градусах).
см. Знайдіть гострий кут ромба (у градусах).
Геометрія. Тест до теми Трапеції, їх види та властивості. Вписані і описані чотирикутники
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Знайдіть середню лінію трапеції, якщо її основи відносяться як 2 : 3, а різниця основ дорівнює 10 см.
|
А |
Б |
В |
Г |
Д |
|
10 см |
15 см |
20 см |
25 см |
30 см |
2. Сума довжин двох протилежних сторін описаного навколо кола чотирикутника дорівнює 45 см. Знайдіть периметр цього чотирикутника (у см).
|
А |
Б |
В |
Г |
Д |
|
70 см |
80 см |
90 см |
100 см |
110 см |
3. Основи рівнобічної трапеції дорівнюють 18 см і 32 см. Знайдіть радіус кола, описаного в трапеції (у см).
|
А |
Б |
В |
Г |
Д |
|
10 см |
12 см |
11 см |
13 см |
15 см |
4. Середня лінія трапеції дорівнює 12 см. Знайдіть більшу основу трапеції (у см), якщо основи відносяться як 1 : 5.
|
А |
В |
В |
Г |
Д |
|
5 см |
10 см |
15 см |
20 см |
25 см |
5. Знайдіть площу круга, вписаного в рівнобедрену трапецію АВСD (АВ || CD), якщо АВ = 4, CD = 16.
|
А |
Б |
В |
Г |
Д |
|
4 |
8 |
12 |
14 |
16 |
6. У трапеції, описаній навколо кола, бічні сторони дорівнюють 5 см і 7 см. Знайдіть довжину (у см) середньої лінії трапецiї.
|
А |
В |
В |
Г |
Д |
|
4 см |
5 см |
6 см |
7 см |
8 см |
7. У рівнобічній трапеції довжини основ дорівнюють 21 см і 9 см, а висота становить 8 см. Знайдіть радіус описаного навколо трапеції кола (у см).
|
А |
Б |
В |
Г |
Д |
|
10 см |
10,625 см |
9,125 см |
9 см |
11 см |
8. Рівнобедрена трапеція MNPQ (MN || PQ) (див. рисунок) описана навколо кола. Відомо, що MN = 2, PQ = 18. Знайдіть радіус кола
|
А |
Б |
В |
Г |
Д |
|
2 |
3 |
4 |
5 |
6 |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між задачами (1 —4) та їх відповідями (А—Д).
|
1 |
Знайдіть периметр рівнобедреної трапеції, якщо гострий кут дорівнює 60, а довжини основ становлять 6 см і 5 см відповідно |
А |
8 см |
|
2 |
Одна з основ трапеції на 2 см менша ніж друга. Знайдіть меншу основу трапеції, якщо її середня лінія дорівнює 15 см |
Б |
10 см |
|
3 |
Одна з основ трапеції становить третину від другої. Знайдіть меншу основу трапеції, якщо її середня лінія дорівнює 20 см |
В |
12 см |
|
4 |
Середня лінія трапеції дорівнює 10 см, а одна з основ — 8 м. Знайдіть другу основу трапеції |
Г |
14 см |
|
|
|
Д |
12 см |
Розв’яжіть завдання 10—12.
10. У рівнобічній трапеції діагональ є бісектрисою гострого кута і ділить середню лінію трапеції на відрізки довжиною 6 см і 12 см. Обчисліть периметр трапеції, у см.
11. Основи рівнобедреної трапеції дорівнюють 3 см і 1 см, а площа трапеції дорівнює 2 см2. Знайдіть гострий кут трапеції (у градусах).
12. Більша основа трапеції дорівнює 18. Знайдіть її меншу основу, якщо відстань між серединами діагоналей дорівнює 4.
Геометрія. Тест до теми Площа чотирикутника.
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Знайдіть площу ромба з діагоналями, які дорівнюють 10 і 16.
|
А |
Б |
В |
Г |
Д |
|
60 |
40 |
100 |
160 |
80 |
2. Площа паралелограма ABCD (див. рисунок) дорівнює 18. Точка К лежить на прямій CD. Знайдіть площу трикутника АВК.
|
А |
Б |
В |
Г |
Д |
|
6 |
8 |
9 |
10 |
12 |
3. Висоти паралелограма 4 і 6 см, а кут між ними дорівнює 30°. Знайдіть площу паралелограма.
|
А |
Б |
В |
Г |
Д |
|
24 см2 |
40 см2 |
48 см2 |
72 см2 |
96 см2 |
4. У трапеції ABCD (див. рисунок) основи ВС і AD відносяться як 1: 3. Знайдіть площу трапеції, якщо площа трикутника BCD дорівнює 4 см2.
|
А |
Б |
В |
Г |
Д |
|
8 см2 |
10 см2 |
12 см2 |
16 см2 |
20 см2 |
5. Площа прямокутника ABCD, зображеного на рисунку, дорівнює 64 см2. Точки Е, F, М і L — середини сторін прямокутника. Знайдіть площу трикутника KLM.
|
А |
Б |
В |
Г |
Д |
|
8 см2 |
16 см2 |
20 см2 |
24 см2 |
32 см2 |
![]()
6. Діагоналі паралелограма дорівнюють 12 см і 10 см, а кут між ними 150°. Знайдіть площу паралелограма (у см2).
|
А |
Б |
В |
Г |
Д |
|
10 см2 |
20 см2 |
30 см2 |
40 см2 |
60 см2 |
7. Периметр ромба дорівнює 20 см, сума довжин його діагоналей дорівнює 14 см. Знайдіть площу ромба (у см2).
|
А |
Б |
В |
Г |
Д |
|
20 см2 |
24 см2 |
28 см2 |
30 см2 |
48 см2 |
8. Знайдіть площу прямокутної трапеції (у см2), в якої різниця основ дорівнює 15 см, а радіус уписаного кола дорівнює 4 см.
|
А |
Б |
В |
Г |
Д |
|
100 см2 |
120 см2 |
130 см2 |
145 см2 |
200 см2 |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку; варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Доберіть до кожного початку речення (1—4) його закінчення (А—Д) так, щоб утворилося правильне твердження.
|
1 |
Площа трапеції дорівнює |
А |
добутку двох його сусідніх сторін |
|
2 |
Площа ромба дорівнює |
Б |
півдобутку його діагоналей |
|
3 |
Площа прямокутника дорівнює |
В |
півдобутку двох його менших сторін |
|
4 |
Площа прямокутного трикутника дорівнює |
Г |
добутку середньої лінії і висоти |
|
|
|
Д |
півдобутку двох його сусідніх сторін |
Розв’яжіть завдання 10—12.
10. Із вершин В і D прямокутника ABCD до діагоналі АС проведені перпендикуляри BE та DF. Відстань між точками Е та F дорівнює б CM, а BE = 4 см. Обчисліть площу прямокутника (у см2).
11. Основи трапеції дорівнюють 11 см і 4 см, а діагоналі — 9 см і 12 см. Знайдіть площу трапеції (у см2).
12. Знайдіть площу рівнобедреної трапеції, описаної навколо кола з радіусом 5, якщо відомо, що бічна сторона трапеції дорівнює 12.
Геометрія. Тест до теми Многокутники та їх властивості
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Скільки утвориться трикутників, якщо в n-кутнику (n > 3) провести з однієї вершини всі його діагоналі?
|
А |
Б |
В |
Г |
Д |
|
n + 1 |
n |
n - 1 |
n - 2 |
n - 3 |
2. Знайдіть суму кутів дванадцятикутника.
|
А |
Б |
В |
Г |
Д |
|
1620° |
1800° |
1980° |
2160° |
2340° |
3. Скільки сторін має многокутник, якщо кожний його зовнішній кут дорівнює 12°?
|
А |
Б |
В |
Г |
Д |
|
5 |
10 |
20 |
30 |
40 |
4. Скільки сторін має многокутник, якщо сума його кутів дорівнює 1440°?
|
А |
Б |
В |
Г |
Д |
|
9 |
10 |
11 |
12 |
13 |
5. Многокутник, зображений на рисунку, складено з трьох рівних квадратів. Знайдіть площу многокутника (у см2), якщо його периметр дорівнює 24 см.
|
А |
Б |
В |
Г |
Д |
|
6 см2 |
7 см2 |
9 см2 |
12 см2 |
27 см2 |
6. Кути п’ятикутника відносяться як 3:4:6:6:8. Знайдіть найбільший кут цього п’ятикутника (у градусах).
|
А |
Б |
В |
Г |
Д |
|
60° |
80° |
100° |
120° |
160° |
7. Сума кутів опуклого многокутника вдвічі менша за суму його зовнішніх кулів, узятих по одному при кожній вершині. Знайдіть число вершин цього многокутника.
|
А |
Б |
В |
Г |
Д |
|
3 |
4 |
5 |
6 |
7 |
8. Кожний із трьох кутів опуклого многокутника дорівнює 80°, а кожний з решти кутів— 150°. Скільки вершин має цей многокутник?
|
А |
Б |
В |
Г |
Д |
|
4 |
5 |
6 |
7 |
8 |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між многокутниками (1 —4) та сумою їх внутрішніх кутів (А—Д).
|
1 |
П’ятикутник |
А |
1800° |
|
2 |
Шестикутник |
Б |
1440° |
|
3 |
Десятикутник |
В |
1080° |
|
4 |
Дванадцятикутник |
Г |
720° |
|
|
|
Д |
540° |
Розв’яжіть завдання 10—12.
10. В опуклому многокутнику 35 діагоналей. Знайдіть суму його внутрішніх кутів у градусах.
11. В опуклому многокутнику сума зовнішніх кутів у 5 разів менша від суми внутрішніх. Знайдіть кількість сторін многокутника
12. В опуклому многокутнику сума його внутрішніх кутів дорівнює 2340°. Знайдіть кількість його діагоналей.
Геометрія. Тест до теми Правильні многокутники та їх властивості.
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, па Вашу думку, відповідь і позначте її у бланку A.
1. Знайдіть внутрішній кут правильного восьмикутника (у градусах).
|
A |
Б |
В |
Г |
Д |
|
45° |
105° |
110° |
125° |
135° |
2. Знайдіть зовнішній кут правильного дванадцятикутника (у градусах).
|
А |
Б |
В |
Г |
Д |
|
30° |
45° |
60° |
90° |
120° |
3. Скільки сторін має правильний многокутник, кожний із внутрішніх кутів якого дорівнює 150°?
|
А |
Б |
В |
Г |
Д |
|
6 |
8 |
10 |
12 |
15 |
4. Скільки сторін має правильний многокутник, кожний із зовнішніх кутів якого дорівнює 36°?
|
А |
В |
В |
1 |
Д |
|
6 |
8 |
10 |
12 |
15 |
5. Скільки сторін має правильний, вписаний у коло многокутник, у якого кожний із центральних кутів кола, що спирається на сторону многокутника, дорівнює 24°?
|
А |
Б |
В |
Г |
Д |
|
6 |
8 |
10 |
12 |
15 |
6. Знайдіть величину кута між найбільшою і найменшою діагоналями правильного шести кутника, проведеними з однієї вершини (у градусах).
|
А |
Б |
В |
Г |
Д |
|
15° |
30° |
45° |
60° |
90° |
7. Знайдіть сторону правильного шестикутника, площа якого дорівнює 6![]() .
.
|
А |
Б |
В |
Г |
Д |
|
1 |
|
2 |
3 |
6 |
8. Радіус кола, описанного навколо правильного трикутника, дорівнює 12![]() . Знайдіть периметр трикутника.
. Знайдіть периметр трикутника.
|
А |
Б |
В |
Г |
Д |
|
18 |
36 |
54 |
72 |
108 |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перетині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між даними правильними многокутниками (1—4) та їх кількістю осей симетрії (А—Д).
|
1 |
Правильний трикутник |
А |
1 вісь |
|
2 |
Правильний чотирикутник |
Б |
3 осі |
|
3 |
Правильний п’ятикутник |
В |
4 осі |
|
4 |
Правильний шестикутник |
Г |
5 осей |
|
|
|
Д |
6 осей |
Розв’яжіть завдання 10—12.
10. Обчисліть площу (у см2) правильного дванадцятикутника, вписаного в коло з радіусом 4 см.
11. Радіуси вписаного і описаного кіл правильного многокутника відповідно дорівнюють 3 см і 2 ![]() см.
см.
Знайдіть периметр Р многокутника. У відповідь запишіть ![]() (у см).
(у см).
12. Радіус кола, описаного навколо правильного многокутника, проведений перпендикулярно до сторони многокутника, ділиться цією стороною навпіл. Знайдіть цей радіус (у см), якщо площа многокутника дорівнює 12 ![]() см2.
см2.
Геометрія. Тест до теми Декартові координати на площині
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Знайдіть рівняння прямої АВ, якщо А (2; 3), В (3; 2).
|
А |
Б |
В |
Г |
Д |
|
у = х + 5 |
у = х- 5 |
у = -х + 5 |
у = -х - 5 |
у = -х |
2. Знайдіть рівняння прямої AВ. якщо вона паралельна осі ОХ і проходить через точку А (3; 4).
|
А |
Б |
В |
Г |
Д |
|
у = 3 |
у = 4 |
у = 5 |
у = 6 |
у = 7 |
3. Знайдіть точку перетину прямих, заданих рівняннями х + у = 4, 3х - у = 0.
|
А |
Б |
В |
Г |
Д |
|
(- 1; - 3) |
(-1; 3) |
(1; - 3) |
(1; 3) |
(3; 1) |
4. Знайдіть рівняння прямої, яка проходить через точку А (-2; 5) і утворює з віссю ОХ кут 45°.
|
А |
Б |
В |
Г |
Д |
|
у = х + 7 |
у = -х + 7 |
у = -х + 3 |
у = х - 3 |
у = х |
5. Знайдіть рівняння прямої АВ, якщо вона паралельна осі ОУ і проходить через точку А (3; 4).
|
А |
Б |
В |
Г |
Д |
|
y = 3 |
х = 4 |
x = 5 |
у = 4 |
x = 3 |
6. Запишіть рівняння кола із центром у точці С (-2; 3), яке проходить через точку А (1; -1).
|
А |
(х - 2)2 + (у - 3)2 = 25 |
|
Б |
(Х + 2)2 + (y - 3)2 = 25 |
|
B |
(х - 2)2 + (у + 3)2 = 25 |
|
Г |
(Х + 2)2 + (у + 3)2 = 25 |
|
Д |
х2 + у2 = 25 |
7. Яка геометрична фігура задана рівнянням x2 + y2 + ax + by + c = 0, ![]() +
+ ![]() - с > 0?
- с > 0?
|
А |
Б |
В |
Г |
Д |
|
точка |
пряма |
коло |
круг |
Визначити неможливо |
8. Знайдіть периметр трикутника, утвореного при перетині осей координат прямою, яку задано рівнянням 4х + 3у = 24.
|
А |
Б |
В |
Г |
Д |
|
6 |
12 |
18 |
24 |
30 |
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку; варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перегині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між рівняннями (1—4) та їх зображенням у декартовій системі координат (А—Д).

Розв’яжіть завдання 10—12.
10. Знайдіть периметр трикутника ABC, якщо А(-1; 2), B(3; -1), С(-1; - 1).
11. Знайдіть радіус кола, заданого рівнянням х2 + у2 - 2х - 2у + 1 = 0.
12. Знайдіть площу чотирикутника ABCD, якщо А(- 1; 3), B(1; 5), С(3; 3), D( 1; 1).
Геометрія. Тест до теми Вектори на площині
Завдання 1—8 мають по п’ять варіантів відповіді, серед яких лише один правильний. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1. Серед векторів ![]() (-2; 4),
(-2; 4), ![]() (2; 2), і
(2; 2), і ![]() (0; -1) та
(0; -1) та ![]() (1; -2) знайдіть колінеарні.
(1; -2) знайдіть колінеарні.
|
А |
Б |
В |
Г |
Д |
|
d і b |
а і d |
а і с |
d і с |
с і b |
2. Знайдіть довжину вектора 3(6; у), якщо відомо, що він колінеарний вектору ![]() , де
, де ![]() (-2;0),
(-2;0), ![]() (0;1).
(0;1).
|
А |
Б |
В |
Г |
Д |
|
7 |
4 |
|
|
6 |
3. На площині дано чотири точки А (1; 2), 5(5; 1), С(3; 4), D (1; -4). Знайдіть кут між векторами ![]() і
і ![]() (у градусах).
(у градусах).
|
А |
Б |
В |
Г |
Д |
|
45° |
30° |
90° |
60° |
120° |
4. Знайдіть кут між векторами ![]() (-1; 2) та
(-1; 2) та ![]() (3; -1).
(3; -1).
|
А |
Б |
В |
Г |
Д |
|
45° |
60° |
90° |
120° |
135° |
5. Визначте величину кута (у градусах) між векторами ![]() якщо відомо, що
якщо відомо, що ![]() (4; 3) та
(4; 3) та ![]() (1; 7), при чому 0°< а < 180°.
(1; 7), при чому 0°< а < 180°.
|
А |
Б |
В |
Г |
Д |
|
30° |
45° |
60° |
90° |
135° |
6. Знайдіть скалярний добуток векторів ![]() , якщо |
, якщо |![]() |= 3, |
|= 3, |![]() |= 8, а кут між векторами дорівнює 120°.
|= 8, а кут між векторами дорівнює 120°.
|
А |
Б |
В |
Г |
Д |
|
- 12 |
-6 |
0 |
6 |
12 |
7. Знайдіть кут (у градусах) між векторами ![]() якщо
якщо ![]() = 10, |
= 10, |![]() |= 4, |
|= 4, |![]() |= 5.
|= 5.
|
А |
Б |
В |
Г |
Д |
|
0° |
30° |
45° |
60° |
90° |
8. Знайдіть координати вектора ![]() якщо А(-2; 3), 5(-8; -5).
якщо А(-2; 3), 5(-8; -5).
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
У завданні 9 до кожного з чотирьох рядків інформації, позначених цифрами, виберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицю відповідей до завдань на перегині відповідних рядків (цифри) і колонок (букви).
9. Установіть відповідність між векторами (1—4), зображеними на рисунку та їх координатами (А—Д).
|
1 |
Вектор |
А |
(3; 0) |
|
2 |
Вектор |
Б |
(-2; -2) |
|
3 |
Вектор |
В |
(2; -2) |
|
4 |
Вектор |
Г |
(2; 2) |
|
|
|
Д |
(-2; 2) |
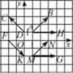
Розв’яжіть завдання 10—12.
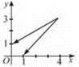 10. У квадраті ABCD сторона АВ дорівнює 1,5 см. Знайдіть скалярний добуток
10. У квадраті ABCD сторона АВ дорівнює 1,5 см. Знайдіть скалярний добуток ![]() ∙
∙ ![]() .
.
11. Обчисліть скалярний добуток векторів, зображених на рисунку.
12. Вектори ![]() утворюють кут 60°,
утворюють кут 60°, ![]() = 1
= 1
Знайдіть значення виразу (![]() )2
)2
ВІДПОВІДІ ДО ТЕМАТИЧНИХ ТЕСТІВ З АЛГЕБРИ
Тема 1. НАТУРАЛЬНІ ЧИСЛА ТА ДІЇ НАД НИМИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
В |
Г |
Г |
Д |
В |
Б |
В |
В |
1-Г ; 2-А; 3-Д; 4-Б |
216 |
8597 |
2762 |
Тема 2. ЗВИЧАЙНІ ДРОБИ, МІШАНІ ЧИСЛА ТА ДІЇ НАД НИМИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Б |
А |
А |
Д |
Г |
Г |
А |
Д |
1-Д ; 2-А; 3-Б; 4-Д |
300 |
112 |
5 |
Тема 3. ДЕСЯТКОВІ ДРОБИ ТА ДІЇ НАД НИМИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Б |
А |
В |
Б |
Г |
Г |
В |
А |
1-Д; 2-А; 3-Б; 4-Г |
372,5 |
120,1 |
78 |
Тема 4. РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ НАД НИМИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Б |
В |
в |
В |
Г |
Г |
В |
В |
1-В; 2-Д; 3-Б; 4-А |
1 |
-4 |
1 |
Тема 5. ВІДСОТКИ. ЗАДАЧІ НА ВІДСОТКИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Б |
В |
Б |
Б |
Г |
Б |
Д |
Г |
1-А; 2-Б; 3-В; 4-Г . |
108 |
400 |
2,7 |
Тема 6. СТЕПІНЬ З НАТУРАЛЬНИМ І ЦІЛИМ ПОКАЗНИКОМ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Б |
Д |
В |
Г |
Г |
А |
В |
Б |
1-Д; 2-В; 3-Г ; 4-Б |
0,0625 |
6 |
2 |
Тема 7. ОДНОЧЛЕНИ ТА ДІЇ НАД НИМИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Б |
В |
Д |
Д |
Г |
В |
Б |
Г |
1-Г; 2-Д; 3-Б; 4-А |
10 |
72 |
1,5 |
Тема 8. МНОГОЧЛЕНИ ТА ДІЇ НАД НИМИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
А |
Д |
Б |
В |
Г |
Д |
Д |
Б |
1-Д; 2-Г; 3-А; 4-Б |
0,9801 |
60 |
4 |
Тема 9. АЛГЕБРАЇЧНІ ДРОБИ ТА ДІЇ НАД НИМИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Б |
В |
В |
В |
Б |
А |
Б |
Д |
1-Б; 2-В; 3-Д; 4-А |
70 |
20 |
12 |
Тема 10. АРИФМЕТИЧНИЙ КВАДРАТНИЙ КОРІНЬ. ДІЙСНІ ЧИСЛА
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Д |
Д |
А |
В |
В |
В |
Д |
Г |
1-Г ; 2-Д; 3-В; 4-Б |
1 |
50 |
1 |
Тема 11. РІВНЯННЯ, НЕРІВНОСТІ ТА ЇХ СИСТЕМИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
В |
Д |
Д |
В |
Г |
Г |
В |
Д |
1-Б; 2-Г; 3-Д; 4-В |
3 |
2 |
- 1 |
Тема 12. ФУНКЦІЇ ТА ЇХ ОСНОВНІ ВЛАСТИВОСТІ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Б |
В |
В |
Б |
В |
Б |
Б |
Д |
1-В; 2-Д; З-A; 4-В |
2 |
3 |
2 |
Тема 13. ЛІНІЙНА ФУНКЦІЯ, ЛІНІЙНІ РІВНЯННЯ, НЕРІВНОСТІ ТА ЇХ СИСТЕМИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Д |
В |
Д |
В |
В |
А |
В |
Г |
1-Г; 2-В; З-A; 4-Д |
1 |
9 |
500 |
Тема 14. КВАДРАТИЧНА ФУНКЦІЯ, КВАДРАТНІ РІВНЯННЯ, НЕРІВНОСТІ ТА ЇХ СИСТЕМИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
А |
Б |
Б |
Г |
Г |
В |
Г |
Д |
1-В; 2-А; 3-Г; 4-В |
-3,5 |
-4 |
-2 |
Тема 15. РАЦІОНАЛЬНІ РІВНЯННЯ, НЕРІВНОСТІ ТА ЇХ СИСТЕМИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
A |
Г |
Б |
Г |
Д |
В |
В |
Д |
1-Г; 2-А; 3-Д; 4-В |
5 |
0,25 |
-3 |
Тема 16. ЧИСЛОВІ ПОСЛІДОВНОСТІ. АРИФМЕТИЧНА ТА ГЕОМЕТРИЧНА ПРОГРЕСІЇ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
В |
Г |
Д |
Б |
Г |
А |
А |
А |
1-Г; 2-Д; 3-A; 4-В |
9 |
54 |
96 |
ВІДПОВІДІ ДО ТЕМАТИЧНИХ ТЕСТІВ З ГЕОМЕТРІЇ
Тема 1. ПОЧАТКОВІ ПОНЯТТЯ ПЛАНІМЕТРІЇ. ГЕОМЕТРИЧНА ФІГУРА. ПОНЯТТЯ ПРО АКСІОМИ, ТЕОРЕМИ, ПОНЯТТЯ ПРО ОБЕРНЕНУ ТЕОРЕМУ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Г |
В |
Д |
А |
В |
Д |
А |
Б |
1-Б; 2-В; 3-Д; 4-А |
7 |
5 |
15 |
Тема 2. КУТИ ТА ЇХ ВИДИ. ВЕЛИЧИНА КУТА ТА ЇЇ ВЛАСТИВОСТІ. СУМІЖНІ І ВЕРТИКАЛЬНІ КУТИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
В |
Б |
Б |
В |
В |
В |
Г |
В |
1-В; 2-Д; 3-А; 4-Г |
90 |
40 |
100 |
Тема 3. ПАРАЛЕЛЬНІ ПРЯМІ І ПРЯМІ, ЩО ПЕРЕТИНАЮТЬСЯ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
В |
Г |
Б |
В |
В |
Б |
Г |
Г |
1-Б; 2-В; 3-Д; 4-А |
165 |
75 |
105 |
Тема 4. ТРИКУТНИКИ ТА ЇХ ВИДИ. ОЗНАКИ РІВНОСТІ ТРИКУТНИКІВ. РІВНОБЕДРЕНИЙ ТРИКУТНИК ТА ЙОГО ВЛАСТИВОСТІ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
В |
А |
Г |
В |
А |
Г |
Г |
Б |
1-Б; 2-В; 3-Г ; 4-А |
6 |
4 |
8 |
Тема 5. СУМА КУТІВ ТРИКУТНИКА
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
В |
В |
Б |
Г |
Г |
Д |
Б |
Г |
1-Д; 2-А; 3-Г; 4-Б |
120 |
122 |
116 |
Тема 6. ПОДІБНІСТЬ ТРИКУТНИКІВ. ТЕОРЕМА ПІФАГОРА
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
В |
В |
г |
Б |
Д |
г |
В |
Г |
1-Д;2-А; 3-Б; 4-В |
144 |
12 |
14 |
Тема 7. ПОНЯТТЯ ПЛОЩІ. ПЛОЩА ТРИКУТНИКА
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Г |
А |
В |
Д |
В |
В |
Б |
Б |
1-Д; 2-Б; 3-Г; 4-А |
150 |
30 |
600 |
Тема 8. КОЛО І КРУГ. ДОТИЧНА ДО КОЛА
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Г |
Д |
Б |
Б |
Д |
А |
В |
В |
1-В; 2-А; 3-Б; 4-Д |
70 |
20 |
12 |
Тема 9. ВПИСАНІ КУТИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
В |
Д |
В |
А |
Д |
Г |
А |
Д |
1-Б; 2-Г; 3-В; 4-А |
70 |
20 |
12 |
Тема 10. ДОЖИНА КОЛА І ПЛОЩА КРУГА.
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
В |
Б |
В |
Г |
Б |
Г |
А |
Б |
1-Г; 2-Д; 3-В; 4-А |
70 |
20 |
12 |
Тема 11. ВПИСАНІ І ОПИСАНІ ТРИКУТНИКИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
В |
В |
В |
Д |
Г |
Б |
Б |
В |
1-Г; 2-Д; 3-Б; 4-А |
2 |
5 |
4 |
Тема 12. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ ГОСТРОГО КУТА ПРЯМОКУТНОГО ТРИКУТНИКА
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
А |
Д |
Б |
В |
Г |
А |
Г |
В |
1-Г ; 2-В; 3-Д; 4-Б |
32 |
3 |
18 |
Тема 13. РОЗВ’ЯЗУВАННЯ ДОВІЛЬНИХ ТРИКУТНИКІВ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
А |
Д |
В |
В |
В |
Г |
А |
Г |
1-Б; 2-А; 3-В; 4-Д |
5 |
45 |
14 |
Тема 14. ПАРАЛЕЛОГРАМИ, ЇХ ВИДИ ТА ВЛАСТИВОСТІ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
В |
Г |
Б |
Г |
В |
А |
Б |
Г |
1-Г; 2-Б; 3-В; 4-А |
50 |
5 |
60 |
Тема 15. ТРАПЕЦІЇ, ЇХ ВИДИ ТА ВЛАСТИВОСТІ. ВПИСАНІ І ОПИСАНІ ЧОТИРИКУТНИКИ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Г |
В |
Б |
Г |
Д |
В |
Б |
Б |
1-В; 2-Г; 3-Б; 4-Д |
60 |
45 |
10 |
Тема 16. ПЛОЩА ЧОТИРИКУТНИКА
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Д |
В |
В |
Г |
Б |
В |
В |
А |
1-Г; 2-В; 3-А;4-В |
40 |
54 |
120 |
Тема 17. МНОГОКУТНИКИ ТА ЇХ ВЛАСТИВОСТІ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Г |
Б |
Г |
Б |
Д |
Д |
А |
Б |
1-Д; 2-Г; 3-Б; 4-А |
1440 |
12 |
90 |
Тема 18. ПРАВИЛЬНІ МНОГОКУТНИКИ ТА ЇХ ВЛАСТИВОСТІ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Д |
А |
Г |
В |
Д |
Б |
В |
Д |
1-Б; 2-В; 3-А;4-Д |
48 |
12 |
4 |
Тема 19. ДЕКАРТОВІ КООРДИНАТИ НА ПЛОЩИНІ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
В |
Б |
Г |
А |
Д |
Б |
В |
Г |
1-Д; 2-Г; 3-Б; 4-А |
12 |
1 |
8 |
Тема 20. ВЕКТОРИ НА ПЛОЩИНІ
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Відповідь |
Б |
Г |
В |
Д |
Б |
А |
Г |
Д |
1-Д; 2-Г; 3-В; 4-А |
225 |
18 |
3 |
ЗРАЗКИ ТЕСТІВ
ТЕСТ ДЛЯ ВСТУПНИХ ВИПРОБУВАНЬ З МАТЕМАТИКИ (БАЗА 9 КЛАСІВ)
|
ВАРІАНТ №1 |
|||||
|
Завдання 1-12 мають по чотири варіанти відповідей, з яких тільки одна правильна. Оберіть правильну, на Вашу думку відповідь та запишіть її. |
|||||
|
№ п/п |
Завдання |
Відповіді |
|||
|
А |
Б |
В |
Г |
||
|
1 |
Обчисліть 0,12 + 1,2 |
1,14 |
1,122 |
1,32 |
0,24 |
|
2 |
Вкажіть добуток коренів квадратного рівняння: |
-6 |
2 |
-3 |
-2 |
|
3 |
Яка з поданих функцій є лінійною |
|
|
|
|
|
4 |
Спростіть вираз |
|
|
|
|
|
5 |
Порівняйте х та у, якщо |
|
|
|
|
|
6 |
Винесіть множник з-під знака кореня |
|
|
|
|
|
7 |
Визначте кутовий коефіцієнт прямої, заданої рівнянням |
1 |
-1 |
3 |
-3 |
|
8 |
Скоротіть дріб
|
|
|
|
|
|
9 |
Яке значення не є допустиме для дробу |
5 |
3 |
5; -3 |
-3 |
|
10 |
Чому дорівнює 15% від числа 300? |
45 |
4,5 |
60 |
20 |
|
11 |
Катет, що лежить проти кута 30° дорівнює 7,5 см. Знайти гіпотенузу трикутника. |
12 |
13 |
14 |
15 |
|
12 |
Знайдіть центр і радіус R кола: |
О1(-2;1) R=9 |
О1(2;-1) R=3 |
О1(-2;1) R=3 |
О1(2;-1)R=9 |
|
Розв’яжіть завдання 13-16 та запишіть відповідь. (виконайте необхідні перетворення та запишіть короткі кроки розв’язку). |
|||||
|
13 |
Спростіть вираз |
||||
|
14 |
Знайдіть суму нескінченної геометричної прогресії 125; -25; 5; … |
||||
|
15 |
Розв’яжіть нерівність |
||||
|
16 |
Знайдіть кути паралелограма зі сторонами 3 см і 12 см, якщо його площа дорівнює 18 см2. |
||||
|
Розв’яжіть завдання з повним обґрунтуванням розв’язку, запишіть відповідь. |
|||||
|
17 |
При яких значеннях m рівняння |
||||
|
18 |
Основи рівнобічної трапеції дорівнюють 22 см і 42 см, а бічна сторона – 26 см. Обчислити радіус описаного кола навколо трапеції. |
||||
ТЕСТ ДЛЯ ВСТУПНИХ ВИПРОБУВАНЬ З МАТЕМАТИКИ (БАЗА 9 КЛАСІВ)
|
ВАРІАНТ №2 |
|||||
|
Завдання 1-12 мають по чотири варіанти відповідей, з яких тільки одна правильна. Оберіть правильну, на Вашу думку відповідь та запишіть її. |
|||||
|
№ п/п |
Завдання |
Відповіді |
|||
|
А |
Б |
В |
Г |
||
|
1 |
Між якими двома послідовними натуральними числами міститься число |
18 і 20 |
3 і 4 |
4 і 5 |
5 і 6 |
|
2 |
Яка з даних лінійних функцій є спадною |
|
|
|
|
|
3 |
Визначте число, що є дільником числа 12 |
24 |
36 |
72 |
6 |
|
4 |
Чому дорівнює сума коренів рівняння |
-5 |
-2 |
-3 |
3 |
|
5 |
Визначте який з дробів більший за |
|
|
|
|
|
6 |
Знайдіть четвертий член геометричної прогресії |
-9 |
9 |
27 |
-27 |
|
7 |
Знайдіть корінь рівняння |
|
|
2 |
|
|
8 |
Спростіть вираз |
|
|
|
|
|
9 |
Подайте добуток у вигляді многочлена |
|
|
|
|
|
10 |
Скоротіть дріб |
|
|
|
|
|
11 |
У Δ АВС, АВ = 12см, АС = 15см, ВС = 26см. Який кут найменший? |
|
|
|
Визначити неможливо |
|
12 |
Довжина кола дорівнює 6πсм. Знайдіть його радіус. |
4см |
3см |
6см |
3πсм |
|
Розв’яжіть завдання 13-16 та запишіть відповідь. (виконайте необхідні перетворення та запишіть короткі кроки розв’язку). |
|||||
|
13 |
Скоротіть дріб |
||||
|
14 |
Пряма |
||||
|
15 |
Розв’яжіть нерівність |
||||
|
16 |
Бісектриса тупого кута паралелограма ділить протилежну сторону на відрізки 8см і 7см (починаючи від вершини гострого кута). Знайдіть периметр паралелограма. |
||||
|
Розв’яжіть завдання з повним обґрунтуванням розв’язку, запишіть відповідь. |
|||||
|
17 |
Знайдіть область визначення функції |
||||
|
18 |
Сторона ромба дорівнює 25см, а його висота дорівнює 24см. Знайдіть діагоналі ромба. |
||||
ТЕСТ ДЛЯ ВСТУПНИХ ВИПРОБУВАНЬ З МАТЕМАТИКИ (БАЗА 9 КЛАСІВ)
|
ВАРІАНТ №3 |
|||||
|
Завдання 1-12 мають по чотири варіанти відповідей, з яких тільки одна правильна. Оберіть правильну, на Вашу думку відповідь та запишіть її. |
|||||
|
№ п/п |
Завдання |
Відповіді |
|||
|
А |
Б |
В |
Г |
||
|
1 |
Яке з чисел є коренем рівняння |
5 |
6 |
7 |
8 |
|
2 |
Знайдіть різницю |
|
|
|
|
|
3 |
Серед наведених чисел укажіть ірраціональне число |
|
|
|
|
|
4 |
Яка з поданих функцій є спадною |
|
|
|
|
|
5 |
Знайдіть значення виразу |
0 |
1 |
2 |
3 |
|
6 |
Розкладіть на множники многочлен |
|
|
|
|
|
7 |
Знайдіть нулі функції |
0;-5 |
-5 |
0 |
5 |
|
8 |
Скільки відсотків становить число 7 від числа 40? |
18% |
16,5% |
17% |
17,5% |
|
9 |
Скоротіть дріб |
|
|
|
|
|
10 |
Знайдіть дискримінант рівняння |
17 |
±9 |
81 |
57 |
|
11 |
Діагональ квадрата дорівнює |
6 |
8 |
12 |
36 |
|
12 |
Знайти градусну міру дуги, яка складає третину кола. |
220˚ |
270˚ |
60˚ |
120˚ |
|
Розв’яжіть завдання 13-16 та запишіть відповідь. (виконайте необхідні перетворення та запишіть короткі кроки розв’язку). |
|||||
|
13 |
Побудуйте графік функції |
||||
|
14 |
Скоротіть дріб |
||||
|
15 |
Розв’яжіть нерівність |
||||
|
16 |
Дві сторони трикутника дорівнюють |
||||
|
Розв’яжіть завдання з повним обґрунтуванням розв’язку, запишіть відповідь. |
|||||
|
17 |
Відомо, що х1 і х2 – корені рівняння |
||||
|
18 |
Знайти площу прямокутного трикутника, якщо точка дотику описаного кола ділить гіпотенузу на відрізки 10см і 13см. |
||||
ТЕСТ ДЛЯ ВСТУПНИХ ВИПРОБУВАНЬ З МАТЕМАТИКИ (БАЗА 9 КЛАСІВ)
|
ВАРІАНТ №4 |
|||||
|
Завдання 1-12 мають по чотири варіанти відповідей, з яких тільки одна правильна. Оберіть правильну, на Вашу думку відповідь та запишіть її. |
|||||
|
№ п/п |
Завдання |
Відповіді |
|||
|
А |
Б |
В |
Г |
||
|
1 |
Знайдіть корінь рівняння |
2 |
4 |
16 |
32 |
|
2 |
Вкажіть число, що є оберненим числу 5 |
-5 |
|
5 |
|
|
3 |
Чому дорівнює значення виразу: |
|
|
2 |
24 |
|
4 |
Яке з даних чисел не є натуральним? |
0 |
1 |
2 |
101 |
|
5 |
Вкажіть десяткове наближення до сотих дріб |
0,50 |
0,46 |
0,47 |
0,45 |
|
6 |
Знайдіть другий член арифметичної прогресії (аn); якщо а1 = 2,1, а різниця d = - 0,7 |
1,4 |
2,8 |
-1,4 |
-2,8 |
|
7 |
Виконайте ділення |
|
|
|
|
|
8 |
Знайдіть значення виразу |
-2 |
2 |
4 |
-4 |
|
9 |
Подайте у вигляді дробу вираз |
|
|
|
|
|
10 |
Знайдіть координати вершини параболи |
(-3;2) |
(3;2) |
(3;-2) |
(-3;-2) |
|
11 |
Чому дорівнює довжина кола з радіусом 1см? |
|
|
|
|
|
12 |
Знайти координати середини відрізка АВ, якщо А(12;-3), В(-8;1) |
(1;2) |
(-1;2) |
(2;-1) |
(2;1) |
|
Розв’яжіть завдання 13-16 та запишіть відповідь. (виконайте необхідні перетворення та запишіть короткі кроки розв’язку). |
|||||
|
13 |
Виконайте ділення |
||||
|
14 |
Знайдіть номер члена арифметичної прогресії, який дорівнює 15, якщо перший її член дорівнює -6, а різниця дорівнює 3. |
||||
|
15 |
Розв’яжіть систему рівнянь |
||||
|
16 |
У прямокутному трикутнику АВС з гіпотенузою АВ знайдіть бісектрису СД, якщо |
||||
|
Розв’яжіть завдання з повним обґрунтуванням розв’язку, запишіть відповідь. |
|||||
|
17 |
Знайдіть значення виразу |
||||
|
18 |
Сторони трикутника = дорівнюють 15см, 20см і 28см. Обчисліть довжину відрізків, на які ділить бісектриса трикутника більшу його сторону. |
||||
1


про публікацію авторської розробки
Додати розробку
