«Методика послідовності вивчення площі геометричних фігур учнями з порушенням інтелектуального розвитку»

ЧЕРНІВЕЦЬКА ОБЛАСНА РАДА

ІНСТИТУТ ПІСЛЯДИПЛОМНОЇ ПЕДАГОГІЧНОЇ ОСВІТИ

ЧЕРНІВЕЦЬКОЇ ОБЛАСТІ

 

РОЗГЛЯНУТО                                                   СХВАЛЕНО

Методичною радою комунального                    Науково-методичною радою

закладу «Чернівецька спеціальна                      Інституту післядипломної педагогічної

загальноосвітня школа-інтернат №4»               освіти Чернівецької області 

Протокол №2                                                       Протокол №______________

від 17.10.2017                                                      від ___________2017

Директор школи______І.І. Коропецький        Директор ІППОЧО _____Г.І. Білянін

 

 

 

 

 

 

 

МЕТОДИЧНИЙ ПОСІБНИК

 

«Методика послідовності вивчення площі геометричних фігур

учнями з порушенням інтелектуального розвитку»

 

 

 

Укладач: Заремба Л.Д. – вчитель математики, заступник директора з навчально-виховної роботи комунального закладу «Чернівецька спеціальна загальноосвітня школа-інтернат №4»

Рецензенти: Біляніна О.Я. – методист науково-методичного центру природничо-математичних дисциплін ІППОЧО Семчук А.Р. – доцент кафедри природничо-математичних дисциплін ІППОЧО, кандидат фізико-математичних наук Коропецький І.І. – директор комунального закладу «Чернівецька спеціальна загальноосвітня школа-інтернат №4», вчитель-методист

 

 

 

 

 

 

Чернівці – 2017

 

№з/п	Зміст	Номери сторінок
1.	Пояснювальна записка………………………………………….	2
2.	Методика послідовності вивчення площі геометричних фігур…	5
3.	Розробка системи уроків з теми:  «Вимірювання і обчислення площі геометричних фігур»……………………………………….	12
4.	Рекомендована література…………………………………………	35

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пояснювальна записка

В даному посібнику на основі проведених досліджень і аналізу літератури пропонується розробка послідовності методичних та навчально-корекційних прийомів, які варто використати при вивченні теми «Вимірювання та обчислення площі геометричних фігур», наведені розробки уроків з використанням особистісно орієнтованих методів навчання. Ми хочемо ознайомити з основними труднощами засвоєння геометричного матеріалу учнями з особливими освітніми потребами, розкрити їх причини, шляхи корекції та профілактики.

Цей матеріал допоможе готуватися до уроків вчителям математики, які працюють в спеціальних школах, школах-інтернатах для дітей з інтелектуальними порушеннями, у загальноосвітніх школах з інклюзивною формою навчання. Сподіваюся, що запропонований матеріал, насамперед, стане в нагоді молодим спеціалістам, дасть змогу планувати уроки відповідно до можливостей класу та індивідуальних особливостей і здібностей кожного учня.

Спостереження i спеціальні дослідження показують, що найбільш розповсюдженими є комбіновані уроки з геометрії (закріплення матеріалу вивченого на попередньому уроці, пояснення нового матеріалу, повторення раніше вивченого матеріалу, самостійні i практичні роботи з формування вмінь i навичок вимірювати i креслити, контроль знань, умінь i навичок).

При підготовці уроку вчитель визначає тему, чітко формулює виховну мету уроку, продумує корекційно-виховні i практичні задачі. Напередодні готує наочні посібники, дидактичний матеріал, креслярські інструменти для проведення практичних poбіт на дошці i в зошитах. Потім відбирає той геометричний матеріал, який потрібно закріпити чи повторити, а також продумує, які нові знання потрібно пояснити учням, над виробленням яких навичок потрібно працювати, які типи завдань i практичних poбіт повинні виконати учні самостійно.

На наступному етапі вчитель намічає основні етапи уроку, розподіляє види завдань i практичних робіт, продумує, які методи i прийоми він буде використовувати на кожному етапі, намічає, знання яких учнів потрібно перевірити чи які вправи дати тому чи іншому учневі, щоб подолати індивідуальні недоліки в засвоєнні геометричного матеріалу. Вчитель також продумує диференційований підхід до різних груп учнів на кожному етапі уроку, для того, щоб максимально використати можливості кожного учня, здійснити навчання в зоні найближчого розвитку. Kpiм того, він обдумує методи i прийоми контролю знань учнів на кожному eтапi (напередодні намічає, знання яких учнів оцінюватиме поурочним балом в кінці уроку, а які учні будуть оцінені за певні види діяльності на час уроку).

Запропоновані методи та прийоми роботи зумовлені завданнями спеціальної школи на сучасному етапі розвитку, змістом навчального матеріалу, віком та рівнем готовності учнів до засвоєння навчального матеріалу.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Методика послідовності вивчення площі геометричних фігур

Згідно з новою програмою учні з інтелектуальними порушеннями у 9-му класі знайомляться з таким поняттям, як площа. Вчитель пояснює, що площа – це одна з основних математичних величин. Він дає означення: площею геометричної фігури називається величина частини площини, яка знаходиться всередині цієї  фігури (рис. 1.)

 

Рисунок 1

 

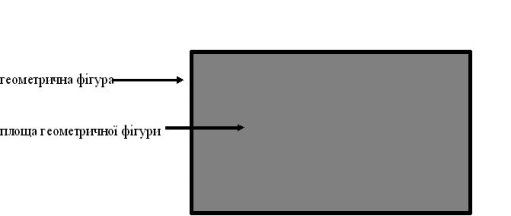
Учні спеціальної школи починають вивчати обчислення площі із прямокутника. Пояснення вчителю потрібно розпочати з накладання меншого чотирикутника на більший. Учням ставлять запитання: «Який з цих чотирикутників більший?». Після того, як школярі дадуть відповідь, вчитель підводить їх до думки, що порівнюються площі, які займають чотирикутники.

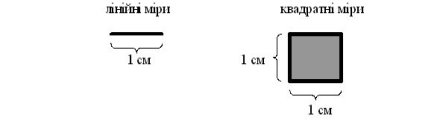
Одиницею вимірювання плоскої геометричної фігури звичайно вважають квадрат зі стороною, що дорівнює одиниці довжини (одиничний квадрат). При вимірюванні площі ставлять у відповідність до неї яке-небудь число, що дорівнює кількості одиниць вимірювання площі. Визначити площу фігури — означає з’ясувати, скільки одиничних квадратів у ній уміщується.

 Дається означення: квадрат з довжиною сторін 1см, називається квадратним сантиметром. Таким чином, щоб визначити площу прямокутника, потрібно розбити його на квадратики (1см) і порахувати суму всіх квадратиків, які лежать усередині прямокутника. Вчитель наводить приклад лінійних і квадратних мір:

 

Спочатку учні вчаться обчислювати площу прямокутників, які накреслені на папері в клітинку. Тут їм легше порахувати квадратні сантиметри і таким чином визначити площу фігури. Поступово вчитель переходить з ними на роботу з нелінованим папером. На ньому вже значно важче виконати такі обчислення. Тому для полегшення роботи він пропонує використовувати палетку — прозору пластинку з нанесеною на неї сіткою квадратиків, яка служить для обчислення площі на планах і картах, а також для обрахунку координат (див. рис. 2.). Накладаючи таку палетку на прямокутники учні швидко перераховують квадратики і визначають їх площу.

 

Рисунок 2.

 

Після цього вчитель пояснює, що обчислювати таким чином площі геометричних фігур не завжди є можливість, оскільки виникає потреба обчислити площу полів, земельних ділянок, лісових угідь тощо. У таких випадках для вирішення цієї проблеми використовують формулу. Для того, щоб пояснити її, вчитель створює проблемну ситуацію: як обчислити площу попередньої фігури, використовуючи палетку? Оскільки діти вже знайомі з даним матеріалом вони швидко вирішують це завдання, полічивши квадратні сантиметри у її середині. Якщо ми повернемось до площі фігури, яку обчислили за допомогою палетки (див. рис. 2.) можна помітити, що її площа дорівнює 28 сантиметрів квадратних. Тепер вчитель пропонує виміряти ширину і довжину даної фігури. Діти отримують відповідно 4 см і 7 см. Педагог записує дію: 7 х 4 =28. Він запитує: «Що я зробив? Правильно, я перемножив довжину прямокутника на його ширину. Скільки квадратиків ви нарахували у прямокутнику? (28). Який я отримав результат? (28). Зверніть увагу, що ми отримали один і той самий результат». Таке пояснення дозволяє вчителю підвести учнів до того, що для обчислення площі, так само, як і периметра, можна застосувати формулу. Він пояснює, що площу позначають латинською літерою S, сторони відповідно двома літерами: а — довжину, b — ширину (або висоту) фігури.

Отже, формула буде мати такий вигляд:  S_прям.=а·b. Далі педагог розповідає, що для обчислення площі потрібно помножити довжину на ширину, тобто взяти 2 величини. Отже, для позначення площі до слова «сантиметри» додається слово «квадратні» (адже ми обчислюємо площу за допомогою квадратиків) і відповідно  вводиться  позначення  «см²»  (квадратні  сантиметри).   Таким чином, запис обчислення площі даного прямокутника буде мати такий вигляд: S_прям.=4 см•7см=28см².

Для закріплення матеріалу потрібно організувати вправи з вимірювання довжин сторін і паралельно обчислення площі різних прямокутників.

Згодом учням пояснюють, що площу можна вимірювати, обчислювати і виконувати з цими числами різні дії. Для цього визначили такі одиниці —квадратний міліметр (мм²), квадратний сантиметр (см²), квадратний дециметр (дм²), квадратний метр (м²), квадратний кілометр (км²), сотка (ар), гектар (га).

Знайомити учнів з різними мірами обчислення площі зразу не потрібно, оскільки вони їх змішують між собою і потім важко диференціюють. Лише після того, як школярі усвідомлять поняття «квадратний сантиметр» вводиться поняття «квадратний дециметр» — квадрат з довжиною сторін 10 см і його позначення — 1 дм²; квадратний метр — квадрат з довжиною сторін 1 м і його позначення – 1 м²; квадратний кілометр — квадрат з довжиною сторін 1000 м — його позначення — 1 км². Для полегшення запам'ятовування можна використати таблицю, яку вивісити перед школярами:

1 мм² — це площа квадрата зі стороною 1 мм. Тобто 1 мм • 1 мм = 1 мм²

1 см² — це площа квадрата зі стороною 1 см. Тобто 1 см • 1 см = 1 см²

1 дм² — це площа квадрата зі стороною 1 дм. Тобто 1 дм • 1 дм = 1 дм²

1 м² — це площа квадрата зі стороною 1 м. Тобто 1 м • 1 м = 1 м²

1 км — це площа квадрата зі стороною 1 км. Тобто 1 км • 1 км = 1 км²

1 сотка — це площа квадрата зі стороною 10 м. Тобто 10 м • 10 м = 100 м² = 1 сотка = 1 ар

1 гектар — це площа квадрата зі стороною 100 м. Тобто 100 м • 100 м = 10000 м² = 1 га

Потрібно сказати, що не всі діти з порушенням інтелектуального розвитку здатні оволодіти даним матеріалом. Деяким з них він просто недоступний в силу об'єктивних причин, які обумовлюються наявністю у них значних інтелектуальних порушень. Але, не зважаючи на це, вчитель повинен пояснювати його основній масі учнів, адже ці знання необхідні як для оволодіння трудовою професією, так і у повсякденному житті. Тому, крім обчислення площі прямокутника, найбільш здібні школярі можуть навчитись обчислювати площі квадрата, паралелограма і трикутника.

Наведемо приклад організації роботи з учнями при вивченні цього матеріалу.

Площа квадрата обчислюється так само, як і площа прямокутника. При цьому потрібно лише звернути увагу школярів на те, що оскільки сторони квадрата рівні, то при обчисленні його площі множимо два однакові числа. Отже, для обчислення площі квадрата використовуємо формулу: S _квад = а·а.

Після цього потрібно познайомити учнів з обчисленням площі інших геометричних фігур. Спочатку вони вчаться обчислювати площу паралелограма. Для цього доцільно виготовити модель (див. рис. 4.).

Рисунок 4.

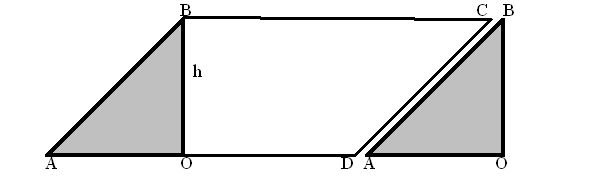
Пояснення можна проводити таким чином: «Нам дано паралелограм АВСD. Для обчислення його площі проведемо в ньому висоту ОВ. Для обчислення площі паралелограма, так само, як для обчислення площ прямокутника і квадрата використовується формула. За формулою, щоб обчислити площу паралелограма АВСD, потрібно його основу (а) помножити на висоту (h), тобто його площа обчислюється за формулою: S_{паралел.} = a·h. У даному паралелограмі висота дорівнює 3 см, основа - 5 см, отже,

S_{паралел.} = 3 см·5см = 15см².

Вчитель пропонує школярам таке пояснення: «Для перевірки правильності виконаного обчислення опустимо перпендикуляр з точки В на основу паралелограма. Оскільки ми вже знаємо, що перпендику­ляр, опущений з вершини геометричної фігури на його основу нази­вається висотою, то в даному випадку ВО - висота паралелограма. Вирізаємо нижицями дану геометричну фігуру. Тепер у неї акуратно відрізаємо ∆АВО і приставляємо його до сторони СD. Яку фігуру ми отримали? Вірно, прямокутник. Тобто, виконавши такі операції, ми з паралелограма утворили прямокутник. Для обчислення площі прямокутника використовується формула: S_{паралел.} = a·b, де а - основа, b - бічна сторона. Оскільки ми вже знаємо, що бічна сторона є його висотою.   Таким   чином,   щоб   виконати   обчислення   площі паралелограма, використовується формула: S_{паралел.} = a·h».

Щоб довести істинність такого обчислення, використовують палетку. Утворені на палетці 3 квадратики, поділені по діагоналі навпіл, можна додати до 12 цілих і знову ж таки отримати результат 15 см². Таким чином, школярам стає зрозуміло, що площа паралелограма обчислюється за даною формулою, оскільки з нього завжди можна утворити прямокутник.

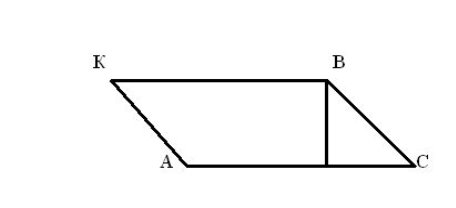
Обчислення площі трикутника є складним матеріалом для дітей з інтелектуальними порушеннями. Його можна вводити лише після того, як учні навчились безпомилково обчислювати площі прямокутника, квадрата, паралелограма. Знайомлячи з ним дітей вчитель пояснює, що для обчислення площі ∆АВС потрібно від верхньої точки (в нашому випадку В) провести паралельно  основі лінію такої ж, як основа, довжини (ВК) (див. рис. 5.). Після цього сполучити між собою точки К і А. Утворився паралелограм АКВС. Оскільки школярі знають, за якою формулою відбувається обчислення площі паралелограма (S = a·h) вони з цим завданням швидко справляються. Але на рисунку чітко видно, що ∆АКВ = ∆АВС. Отже, для того, щоб обчислити площу ∆АВС потрібно площу паралелограма АКВС поділити на 2. Після цього вчитель робить висновок: для обчислення площі трикутника використовують формулу: S_трик. = a·h:2

Рисунок 5.

Після формування в учнів знань про обчислення площі квадрата вчитель знайомить їх з величинами, які використовуються для вимірювання площ полів. Він пояснює, що для позначення площі полів квадратний метр є малою величиною, а квадратний кілометр – великою. Тому в практиці прийнято використовувати такі позначення площі, як гектар і ар.

Ар - це квадрат з довжиною сторін 10 м. Населення в своєму мовленні часто використовує інший термін – «сотка». І тому якщо кажуть, що біля садиби є 8 соток — це означає, що біля садиби є 8 арів (скорочено ар позначають однією літерою а). Тобто біля садиби є площа, яка дорівнює величині 8 квадратів з довжиною сторін 10 м.

Гектар – це квадрат з довжиною сторін 100 м. Гектарами в більшості випадків вимірюють площі полів сільськогосподарських підприємств. Наприклад, зібрати врожай 68 ц з гектара означає, що з квадрата землі, сторона якого 100 метрів, зібрали 6 тон і 8 центнерів зерна.

Вчителю спеціальної школи потрібно так організувати процес навчання наочної геометрії, щоб подолати характерні помилки (чи уникнути їх) і труднощі в оволодінні учнями геометричними знаннями, вміннями і навичками.

Ставлячи перед школярами певні завдання, вчитель повинен бути впевнений в тому чи зможуть вони їх вирішити, чи наявні в них необхідні навички та вміння. Ці знання допомагають педагогу оптимізувати навчальний процес – матеріал поділити на більші або менші навчальні одиниці, надати учням певні підказки для розв'язання поставлених проблем, організувати систему навідних запитань тощо, тобто проводити диференційований та індивідуальний підхід на уроках і в позаурочний час.

Але це лише один бік проблеми. Інший полягає в тому, що потрібно всіма наявними у розпорядженні педагога засобами розвивати пізнавальні можливості учнів; корегувати їх. При цьому можна використовувати два шляхи – надати процесу навчання навчаючого характеру і використання: спеціальних вправ, як корекційного, так і тренувального характеру. Психологічними дослідженнями (Л.С.Виготський, В.Занков, Г.С.Костюк) доведено, що лише там навчання є розвиваючим, де воно виступає, як спільна діяльність педагога і учнів. Якщо ж педагог максимальну активність бере на себе або надто спрощує процес подання нового матеріалу, мислення дитини не дістає оптимального навантаження і, отже, не розвивається повною мірою.

 

 

 

 

 

 

 

Розробка системи уроків з теми:

«Вимірювання і обчислення площі геометричних фігур».

Передмова

Урок є основною формою організації навчальної та корекційно-виховної роботи як в масовій загальноосвітній школі, так і в спеціальній школі. Проте в спеціальній школі урок має свою специфіку, зумовлену особливостями пізнавальної діяльності учнів і завданнями корекційно-виховної роботи школи, а саме:

1.  На уроках у спеціальній школі, крім загальноосвітніх та виховних завдань, однакових з масовою школою, розв'язуються інші завдання, властиві тільки спеціальному закладу освіти: відбувається компенсація й корекція вад розвитку дітей. Тільки завдяки цьому стає можливим загальний розвиток особистості дитини з порушенням інтелекту і формування в неї духовних і фізичних якостей.
2.  У зв'язку з труднощами в роботі з дітьми з порушеннями інтелекту, а також з наявністю великої нерівномірності в розвитку пізнавальних сил і здібностей кожного школяра, кількість учнів у класах спеціальної школи набагато менша, ніж у масовій. Вона не повинна перевищувати 12 осіб. При такій наповнюваності класу вчитель може приділяти максимум уваги кожному учневі, здійснювати індивідуальний підхід без серйозних порушень фронтальної організації праці.
3.  Класи у спеціальному закладі комплектують з урахуванням не тільки віку, а й ступеня розвитку інтелекту дитини. До навчання залучають дітей лише з легкими формами розумової відсталості. Через те в одному і тому класі можуть навчатися учні різного віку. Різниця у віці може становити до двох років.
4.  Враховуючи низьку продуктивність пізнавальної діяльності учнів, на кожен урок визначають значно менший обсяг матеріалу порівняно з масовою школою. Крім того, цей матеріал спеціально опрацьовують, щоб він був доступний для учнів з інтелектуальними порушеннями.
5.  Певні особливості є і в доборі форм і методів навчальної роботи: широко практикуються повторення вивченого, ігрові моменти; навчання здебільшого відбувається на практичній основі: складні системи знань подаються в розчленованому вигляді, відповідно і діяльність учнів також набуває розчленованого характеру, особливо на початкових етапах навчання.
6.  В організації учнів особливо велику роль відіграють безпосереднє керівництво і пряма допомога вчителя, а у молодших класах це зводиться до патронування кожної дії учнів.

У спеціальній школі урок включається в систему охоронно-педагогічного режиму. На ньому створюються найсприятливіші умови для захисту ослабленої нервової системи і психіки дитини від надмірних подразнень, різких змін в умовах перевтоми, появи астенічних емоцій тощо. Урок регламентований навчальною програмою і шкільним розкладом.

Тема уроку: Ознайомлення із поняттям площі.

Мета:

•      ознайомити учнів із поняттям площі;
•      формувати вміння порівнювати площі фігур, вирізаних із кольорового картону, зображених в зошитах чи на дошці, фігур, що їх оточують;
•      сприяти розвитку порівняння, аналізу у дітей;

•      корегувати недоліки просторової уяви, окоміру учнів
  Обладнання: геометричні фігури, вирізані із кольорового картону, таблиця із зображенням фігур, нелінований папір.

Епіграф до уроку:

«Я чую – і забуваю.

Я слухаю – і я запам'ятовую.

Я дію – і я розумію».

Китайська мудрість.

Хід уроку.

1. Організація учнів на урок.

Перевірити готовність учнів до уроку геометрії, зосередити увагу учнів та

налаштувати на роботу грою: «Впізнай і назви лінії на таблиці»

 

 

2. Актуалізація опорних знань учнів.

• Які лінії знаєте? (Ми знаємо прямі, криві, ламані лінії);
• Виберіть із таблиці тільки прямі лінії;
• Яка це пряма лінія? (Що не має ні початку, ні кінця);
• А відрізок - це пряма лінія? (Так, відрізок - це частина прямої, що має початок і має кінець);
• Які ще частини прямої ви бачите на таблиці? (Промені);
• Які ще лінії є на таблиці? (Криві і ламані лінії);
• Покажіть всі ламані лінії, з чого вони складаються? ((2), (13), (14) -
  ламані лінії, складаються з відрізків, які послідовно з'єднані між собою);
• Покажіть всі криві лінії. ((3), (9), (15));
• Чим відрізняється фігура за номером (7) від фігури за номером (9)?
  (Фігура (9) - крива лінія (ободок), коло, а (7) - круг - частина площини, що обмежена колом);
• Чи відрізняється фігура (4) від фігури (14)? ((4) - трикутник, частина
  площини, яка обмежена замкненою ламаною лінією із 3-х відрізків, а (14) - замкнена ламана лінія).

3. Повідомлення теми, мети уроку.

Вчитель показує на таблиці фігуру за номером (11) і повідомляє, що частину площини, яка обмежена замкненою лінією із п'яти відрізків ще називаються площею п'ятикутника. Тоді вчитель показує частину площини трикутника, прямокутника (на таблиці) і повідомляє, що сьогодні ми ознайомимось із поняттям площі.

Запишіть тему уроку в зошитах.

4. Повідомлення нового матеріалу.

Вчитель бере в руки 2 чотирикутники різної величини і просить взяти учнів такі ж чотирикутники.

- Покажіть частину площини малого і частину площини великого
чотирикутника та їх межу.

- Як порівняти ці чотирикутники? (Шляхом накладання)
Діти порівнюють чотирикутники, а вчитель повідомляє:

- В такому разі говорять, що площа малого чотирикутника менша від площі великого.

5. Первинне закріплення нового матеріалу.

•      Виберіть із  фігур, що знаходиться у вас на парті, круг та
  трикутник.
•      Покажіть частину площини круга, частину площини трикутника
  (їх межу).
•      Порівняйте площі фігур.
•      Що можна сказати про їх площу? (Площа трикутника менша від площі круга)
•      Форму якої фігури вам нагадує кришка парти?
•      Форму якої фігури нагадує вам дошка?
•      Покажіть частину площини кришки парти.
•      Покажіть частину площини дошки.

- Порівняйте площі кришки, парти і дошки.
6. Виконання практичної операції.

Робота з підручником.

•      Побудуйте в зошитах квадрат із стороною 3 см та прямокутник із
  сторонами 3 см і 5 см. Площа якої фігури більша і чому?
•      Чим скористаємось для побудови фігур? (Креслярський косинець, олівець, лінійка)
•      Для чого нам креслярський косинець? (Для побудови прямих
  кутів)
•      Що ми називаємо прямокутником? (Прямокутник - це
  паралелограм, у якого всі кути прямі)
•      Що ми називаємо квадратом? (Квадрат - це прямокутник, у якого
  всі сторони рівні)
•      Чим відрізняється квадрат від прямокутника? (У квадрата всі
  сторони рівні, а у прямокутника тільки протилежні сторони рівні)

Один учень побудову здійснює на дошці.

- Якими мірами довжини користуємось при кресленні на дошці? (Дециметрами)

• Чому? (Щоб збільшити зображення)
• У скільки разів? (У 10 разів)
  Після побудови:

•      Площа якої фігури більша? (Площа прямокутника)
•      Чому? (Прямокутник більший за квадрат)

7. Повторення, узагальнення і систематизація знань учнів.

• З чим ознайомимось сьогодні на уроці? (Із поняттям площі фігури)
• Порівняйте площу підлоги в класі і площу стелі.
• Форму якої фігури вони нагадують? (Прямокутника)

- То яка фігура займає більшу площу? (Підлога і стеля займають однакову
площу, вони рівні)

Завдання на нелінованому папері.

Побудуйте круг радіусом 3 см, та квадрат із стороною 6 см. Вирізавши їх, порівняйте площу фігур.

•      Чим скористаєтесь для побудови круга? (Циркулем,  олівцем, лінійкою)
•      Чим скористаєтесь для побудови квадрата? (Креслярським косинцем, лінійкою, олівцем)
•      Що займає більшу площу спортзал чи стадіон? (Стадіон)
•      Чому? (Стадіон більший від спортзалу)
•      Що займає меншу площу Чернівці чи Україна? Чому?

8. Домашнє завдання (кожному учневі дати завдання на виготовлення
   певної фігури з кольорового картону)
9. Підведення підсумків уроку.

• Що навчилися порівнювати на уроці? (Площу фігур)
• Як порівняти площу фігур? (Перевірити, яка фігура більша чи менша)
• Порівняйте площу обгортки зошита і площу обкладинки книги.
• Площу стенду і площу підвиконника.
• Площу, яку займає подвір'я школи і площу, яку займає наша вулиця.
• Мотивація оцінок.

Тема уроку: Поняття про площу. Палетка.

Мета:

- відтворити знання учнів про лінійні міри та геометричні фігури, як
підготовку до ознайомлення з новим матеріалом;

• дати поняття про площу, палетку;
• формувати у дітей практичні вміння і навики вимірювати площу фігур за допомогою палетки;
• корегувати недоліки просторової уяви у дітей;
• розвивати дрібну моторику пальців рук, окомір;
• збагатити геометричний словник словами площа, палетка.

Обладнання:   многокутники  різних   кольорів,   вирізані  з  кольорового картону; рівновеликі прямокутники; фігури вирізані з паперу в клітинку; палетка, поділена на малі квадрати; палетка, поділена на великі квадрати.

Хід уроку.

1. Організація учнів на урок. Нервово-психологічна підготовка учнів до уроку.

Зосередити увагу учнів, налаштувати на роботу. Перевірити наявність робочого приладдя у кожного учня.

2.   Перевірка домашнього завдання.
3.   Актуалізація опорних знань учнів.

1). Фронтальне опитування учнів (3 вимогою давати відповіді повним реченням).

• Який зараз урок? (геометрія).
• Що вивчаємо на уроках геометрії? (лінії, геометричні фігури).
• Які лінії знаєте? (Ми знаємо прямі, криві, ламані лінії).
• Яка це пряма лінія? (Що не має ні початку, ні кінця).
• Чим відрізняється пряма від відрізка? (Відрізок - це частина прямої, що має початок і має кінець).
• Чи можна виміряти пряму? Відрізок? Чому?
• Якими мірами вимірюємо відрізки? (мірами довжини).
• Назвіть міри довжини і покажіть на масштабній лінійці.

- Які геометричні фігури вивчили? (якщо відповідають «трикутники», «чотирикутники» і «прямокутники» ... – то запитати: «Як їх можна назвати одним словом?» (Многокутники)

2) Провести рукою по кришці стола і запитати: Що я показала? (частину площини кришки стола.)

Завдання дітям: покажіть в класі частину площини кришки парти, частину площини дошки (один учень показує), частину площини підвіконника... Яку фігуру вам нагадують ці предмети? (прямокутник)

3). Показати учням моделі геометричних фігур, а саме: прямокутник, квадрат, трикутник, п'ятикутник) і запитати: «Яка фігура перед вами? Що ми називаємо чотирикутником? Трикутником? (Частину площини, яка обмежена ламаною лінією із 4-х відрізків) Покажіть ці фігури на таблиці».

- Який висновок робимо? (геометричні фігури є частиною площини і належать їй).

4.  Повідомлення теми, мети уроку.

 Вчитель бере в руки моделі трикутника і чотирикутника різних кольорів і запитує:

- Яка фігура більша? Як переконатися?

Тоді накладає одну геометричну фігуру на іншу.  Трикутник повністю міститься всередині чотирикутника.

Вчитель: В такому випадку говорять, що площа чотирикутника більша від площі трикутника (показує площу)

Сьогодні ви ознайомитесь із поняттям площі геометричних фігур. Запишемо слово «площа»у словник та тему уроку: Поняття про площу.

5. Повідомлення нового матеріалу.

а) Завдання дітям (на розвиток окоміру)

- порівняйте площу кришки стола і площу дошки, площу стелі і площу підлоги.

б) Вчитель пропонує порівняти площі двох рівновеликих, але не рівних прямокутників, їх порівняння неможливе (одна фігура не міститься всередині іншої)

Тоді вчитель повертає фігури і учні бачать, що з іншої сторони прямокутники поділені на однакові квадрати.

Учні рахують квадрати і роблять висновок про рівність площ цих прямокутників.

Вчитель: площа першого прямокутника дорівнює 6 однаковим квадратам або 6 квадратним одиницям і площа другого прямокутника дорівнює 6 квадратним одиницям) скороч. = 6 кв.од.

6. Первинне закріплення нового матеріалу.

а)  Учням пропонується виміряти площі геометричних фігур, які вирізані із
паперу в клітинку. Вони перераховують число клітинок, яке вміщується в кожній
фігурі і їх кількості записують в квадратних одиницях. (на дошці і в зошиті)

б) Вчитель: «Як виміряти площу фігури, яка зображена на альбомному листку?»

Діти: «Поділити на квадрати»

Вчитель: «Які квадрати? Різні?»

Діти: «Однакові величини».

Вчитель дає можливість учням зробити це самостійно. Після не дуже вдалої спроби учнів, вчитель повідомляє, що для полегшення роботи використовують палетку (показує її) - прозору плівку, поділену на однакові квадрати. Показує, як правильно виміряти площу фігури за допомогою палетки. Тоді показує палетку, поділену на малі квадрати на більші квадрати, ще більші квадрати. Тоді діти слово «палетка» записують у словник.

7.  Виконання практичних операцій.

а)  - Що вчимося вимірювати? (Площу геометричної фігури)

- За допомогою чого ми вимірюємо площу? (За допомогою квадратів)

- Чим полегшуємо свою роботу? (Палеткою)

б) Робота з підручником.

Завдання 1. Накреслити прямокутник і виміряти його площу.

(кожен учень креслить прямокутник з різною площею)

Не у всіх дітей вийдуть цілими всі квадрати. Тоді вчитель пропонує спочатку порахувати цілі квадрати, а потім частини. Кількість частин поділити пополам (на 2) і додати отриманий результат до цілих квадратів.

Працювати з кожним учнем. Особливо з акалькуліками.

Завдання 2. Накреслити довільний чотирикутник і виміряти його площу за допомогою палетки.

Над цим завданням основна група працює самостійно. З рештою - працює вчитель.

8. Повторення, узагальнення і систематизація знань учнів.

Завдання 3. Накресліть довільний трикутник і виміряйте його площу. Викликати 1 учня до дошки. Нагадую, як правильно тримати метрову лінійку. Він креслить довільний трикутник.

- Які квадрати використовуємо для вимірювання площі? (великі) Викликаємо одного учня до дошки.

Покажи на таблиці трикутник, покажи сторони трикутника. Запитання до класу. Якими мірами вимірюємо сторони трикутника? (лінійними мірами, за допомогою відрізків)

- Якими мірами вимірюємо площу трикутника? (за допомогою квадратів).

9.  Домашнє завдання

Виготовити по 2 прямокутники із довжиною сторін 3 см і 6 см.

10. Підведення підсумків уроку.

• Над якою темою працювали? (вимірювати площу геометричних фігур)
• Як виміряти площу геометричної фігури? (порахувати кількість квадратів, які вміщуються всередині фігури)
• Яких квадратів? Різних? (однакової величини)
• Мотивація оцінок.

Тема уроку: Одиниці площі (см²) Позначення S.

Мета:

• вчити учнів вимірювати площу фігур за допомогою палетки;
• ознайомити з одиницею площі - квадратним сантиметром;
• виховувати вміння використовувати набуті знання на практиці;
• сприяти розвитку вміння аналізувати, порівнювати, розвивати окомір.

Обладнання: палетка поділена на малі квадрати, великі квадрати, ще

більші квадрати; палетка поділена на квадратні сантиметри; квадрати із сторонами 1см; відрізки довжиною 1см; таблиця геометричних фігур і ліній; прямокутники однакової величини.

Хід уроку.

1. Організація учнів на урок.

Перевірити готовність учнів до уроку геометрії. Переключити увагу учнів на себе, зацікавити учнів грою: «Порахуй кількість трикутників на малюнку, кількість чотирикутників, п'ятикутників, яких фігур більше?»

2. Актуалізація опорних знань учнів.

Фронтальне  опитування  учнів (з вимогою давати відповіді повними реченнями)

• Який зараз урок? (геометрія).
• Що вивчаємо на уроках геометрії? (лінії, геометричні фігури).
• Покажіть на таблиці лінії, які вивчили і назвіть їх.

Діти показують прямі лінії (відрізки, промені, криві лінії, ламані лінії).

- Чим відрізняється пряма від відрізка? (Відрізок - це частина прямої, що
має початок і має кінець).

- Покажіть і назвіть геометричні фігури, зображені на таблиці. (1 учень
показує. Інші виправляють, якщо є помилки).

- Покажіть сторони геометричної фігури.

- Якими мірами вимірюємо сторони геометричної фігури?  (лінійними
вимірами)

• Назвіть лінійні міри. (1мм, 1см, 1дм, 1м, 1км)
• Покажіть на масштабній лінійці відрізок довжиною 1см.
• Що навчилися вимірювати на минулому уроці? (площу геометричної
  фігури)
• За допомогою чого ми вимірювали площу? (за допомогою палетки)
• Що таке палетка? Для чого вона? (Палетка - прозора плівка, поділена на однакові квадрати. За допомогою палетки вимірюють площу геометричної фігури).
• Як виміряти площу геометричної фігури? (Порахувати кількість квадратів, які вміщуються всередині фігури).

3.  Повідомлення теми, мети уроку.

Сьогодні ми продовжимо вимірювати площу геометричних фігур, і площу будемо позначати латинською літерою S. Запис теми в зошитах. Вчитель роздає всім учням прямокутники однакової величини, які вони виготовили самостійно та палетки поділені на великі квадрати, менші, і ще менші квадрати. Запитання до дітей:

- Яку фігуру ви бачите перед собою? (Перед собою ми бачимо прямокутник)

- Що називаємо прямокутником? (Прямокутник — це чотирикутник, у якого всі кути прямі)

4.  Повідомлення нового матеріалу.

Виміряйте площу вашого прямокутника, використавши умовне позначення площі через S= …  (на дошці записати). У всіх дітей площа прямокутника вийде різною, хоч всі прямокутники однакової величини.

Запитання до дітей: «Чому так сталося?»

Діти (Тому, що вимірювали площу прямокутника квадратами різної величини).

Вчитель: «Як точно виміряти площу прямокутника?»

Для того, щоб точно виміряти площу, у світі користуються єдиними квадратними мірами. Зокрема, площу квадрата із стороною 1 см називають одним квадратним сантиметром і скорочено позначають 1 кв. см або 1 см².

 

Вчитель показує квадрати із сторонами 1 см і відрізки довжиною 1см та роздає кожному учневі.

• Чим відрізняється 1 кв. см від 1 см? (1 кв. см - квадрат, 1 см -відрізок)
• Завдання дітям: виберіть палетку, яка поділена на квадратні сантиметри і виміряйте площу вашого прямокутника.
• Як вибрати потрібну палетку? (шляхом накладання квадрата із стороною 1 см на палетку)
• Якими мірами скористаєтесь при вимірюванні? (квадратними сантиметрами)
• На дошці записати: S_ = 18 кв.см. Такий запис зрозуміють на Україні,  а S=18 см²  зрозуміють в усьому світі.

5.  Первинне закріплення нового матеріалу.

• Накресліть відрізок довжиною 1 см, накресліть 1 см², накресліть 2 см², два відрізки довжиною по 2 см.
• Про які квадратні одиниці дізналися? (про квадратні сантиметри)
• Для чого нам квадратні сантиметри? (щоб точно вимірювати площу геометричної фігури)
• Якою латинською літерою позначають площу? (площу позначають латинською літерою S.

6.  Виконання практичної операції.

• Ширина листка у блокнота дорівнює 8 см, довжина 5 см. Яку площу займає листок блокнота?
• Форму якої фігури має листок блокнота? (Форму прямокутника)
• Як нам виміряти площу даного прямокутника (накреслити його і виміряти за допомогою палетки)
• В яких мірах будемо вимірювати площу листка блокнота? (за допомогою квадратних сантиметрів)

Основна група завдання виконує самостійно.

Зі слабшою групою - працювати з кожним окремо.(Sкв.= 8см · 5см = 40 см^{2 )}

7. Повторення, узагальнення і систематизація знань учнів.

- Виміряйте площу довільного п’ятикутника. Вчитель нагадує учням, як правильно будувати п'ятикутник, (акалькулікам окреме завдання, виміряти площу моделі п'ятикутника).

8. Домашнє завдання (диференційовано).
9. Підведення підсумків уроку.

• Про що дізналися сьогодні на уроці?
• Якою латинською літерою позначають площу?
• Яку одиницю площі використовували на уроці?
• Для чого нам потрібні квадратні сантиметри?
• Як виміряти площу геометричної фігури? (порахувати квадратні сантиметри у середині геометричної фігури)
• Мотивація оцінок.

 

 

 

Тема уроку: Обчислення площі прямокутника S = а х b.

Мета:   

- навчити учнів обчислювати площу прямокутника за допомогою  формули  S= а х b, де а - довжина прямокутника, b - ширина прямокутника;

- відтворити знання дітей про обчислення периметра, як підготовку до сприймання нового матеріалу;

- виховувати вміння використовувати набуті теоретичні знання на практиці;

- сприяти розвитку аналізу, порівняння, окоміру, просторової уяви.

 Обладнання:  таблиця  з многокутниками,  великі листки нелінованого паперу, креслярські косинці.

Хід уроку.

1. Організація учнів на урок.

 Перевірити наявність робочого приладдя.

 Нервово-психологічна підготовка учнів до уроку.

 Відгадайте загадки: 

Я - невидимка. В цьому суть моя.

Хоч і одна - відома всім і звична.

Фігура я геометрична.

Коли ж багато нас до гурту залучити.

Фігури різні можна утворити.

(Точка)

Я тут. Я нині вертикальна.

Похилою буваю Я.

А можу і лягти горизонтально.

(Пряма)

Мороки завдавати не боюся

Дорослим і малим.

Частина площини я і маю три кути,

Які дорівнюють у сумі двом прямим.

(Трикутник)

У мене є чотири сторони

 Однаковісінької довжини.

Кути мої, без сумніву, прямі

І повідомити вам рад.

Що різну площу міряю підряд.

(Квадрат)

 2. Перевірка домашнього завдання.

 3. Актуалізація опорних знань учнів.

1) Завдання дітям: на таблиці показати межу вказаних многокутників.

- Як називаються замкнені лінії, які ви показали? (ламані)

- Чим є така лінія для геометричної фігури? (Межею)

- Якими мірами вимірюється межа? (Мірами довжини)

- Як обчислити довжину межі? (Виміряти довжину кожної сторони, одержані числа додати)

- Як називається отримана сума? (Периметр)

- Що називається периметром многокутника? (Периметр многокутника - це число, що дорівнює сумі довжин сторін многокутника)

- Якими мірами виражається периметр? (Лінійними)

- Назвіть лінійні міри. (1мм, 1см, Ідм, їм, 1км)

- Чи можна лінійними мірами вимірювати площу? Чому? (лінійні міри - це відрізки, вимірюють довжину відрізків, а не площу фігур.)

- Якими мірами вимірюють площу? (Площу вимірюють квадратними мірами).

- З якою квадратною одиницею ознайомилися на минулому уроці? (квадратним сантиметром)

- Накресліть в зошиті 1 см².

- Сьогодні ми продовжимо вимірювати та навчимося обчислювати площу прямокутника.

4.  Повідомлення теми, мети уроку.

- Запишемо тему уроку: «Обчислення площі прямокутника».

 Вчитель роздає учням прямокутники однакової величини і пропонує виміряти площу.

- Чим скористаєтесь для вимірювання площі прямокутника? (палеткою)

- На які квадратні одиниці поділена палетка? (на квадратні сангиметри)

- Як виміряти площу прямокутника? (Порахувати кількість квадратних сантиметрів, які вміщуються всередині прямокутника)

5.  Повідомлення нового матеріалу.

 У всіх дітей площа прямокутника дорівнюватиме 24 см. Тоді вчитель пропонує виміряти довжину і ширину даної фігури. Вони отримають відповідно 6 см і 4 см.

- Яке число ми отримаємо, якщо перемножимо 6 на 4? (24)

Тобто, для того, щоб обчислити площу прямокутника, не використовуючи палетку, досить перемножити довжину прямокутника на ширину.

- Площа нашого прямокутника 6 см х 4 см = 24 см².

- Запишіть формулу обчислення площі прямокутника.  S = а х b

де S - площа, а - довжина, b - ширина (або висота) прямокутника.

6.  Первинне закріплення нового матеріалу.
    Робота з підручником.

Завдання 1. Побудувати прямокутник із сторонами 3 см і 8 см. Обчислити площу даного прямокутника.

• В яких мірах обчислюємо площу? (В квадратних )
• В яких мірах обчислюємо периметр? (В лінійних мірах)
• Що нам потрібно для побудови прямокутника? (Креслярський косинець, лінійка, олівець)
• Що називається прямокутником? (Прямокутник - це чотирикутник, у якого всі кути прямі)
• Як обчислити площу прямокутника (периметр)? (Довжину помножити на ширину, додати довжини всіх сторін) S = 3 см х 8 см = 24 см²; Р = 3 см + 8 см + 3 см + 8 см = 22 см. З акалькуліками працювати окремо.

7.  Виконання практичної операції.

Завдання 2. Виготовити листки для альбому молодшим школярам. Обчислити площу виготовленого листка. Вчитель роздає кожному учневі листок нелінованого паперу.

- Якої форми повинні бути листки? (Прямокутної)

- Всі листки яку площу повинні мати однакову чи різну? (Всі листки в альбомі однакові)

- Довжина альбомного листка 30 см, ширина 20 см.

- Що потрібно для виготовлення листка? (Креслярський косинець, лінійка, ножиці, олівець)

Після виготовлення листка учні обчислюють площу за формулою. S = 30 см х 20 см = 600 см².

8. Домашнє завдання (диференційовано).

9. Підведення підсумків уроку.

- Над якою темою працювали на уроці? (Обчислювали площу прямокутника)

- Як обчислити площу прямокутника? (Щоб обчислити площу прямокутника, потрібно довжину помножити на ширину)

- Як обчислити периметр многокутника? (Щоб обчислити периметр многокутника, потрібно додати довжини всіх сторін многокутника)

- Обчислити площу і периметр прямокутника із сторонами 3 см і 5 см (усно)

Мотивація оцінок.

Тема уроку. Одиниці площі ( 1 мм², 1 см², 1 дм², 1 м², 1км²) Обчислення площі квадрата.

 Мета:

відтворити знання учнів про обчислення площі прямокутника та одиницю площі 1 см², як основу перед сприйманням нового матеріалу;

ознайомити учнів з одиницями площі;

формувати в учнів практичні вміння і навички;

розвивати просторову уяву, вміння порівнювати, аналізувати.

Обладнання: квадрати із сторонами 1 мм, квадрати із сторонами 1 см, квадрати із сторонами 1дм, квадрат із стороною 1 м, квадрати, зображені на міліметровому папері. Відрізки довжиною 1мм, 1дм, 1см.

 Таблиця із записами:

Один квадратний міліметр	1 кв. мм	1мм2
Один квадратний сантиметр	1 кв. см	1см2
Один квадратний дециметр	1 кв. дм	1дм2
Один квадратний метр	1 кв. м	1м2
Один квадратний кілометр	1 кв. км	1км2

 

Хід уроку.

1. Організація учнів на урок.

Перевірити готовність учнів до уроку, зосередити їх увагу.

Нервово-психологічна підготовка учнів до уроку.

Гра: впізнай квадрат на малюнку.

Що ми називаємо квадратом? (Квадрат - це прямокутник, у якого всі сторони рівні)

2. Перевірка домашнього завдання.

3.Актуалізація опорних знань учнів.

- Що ми вивчаємо на уроці геометрії?

- Які лінії ми вивчаємо?

- Яка це пряма лінія?

- Чим відрізняється пряма від відрізка?

- Якими мірами вимірюємо відрізки?

- Назвіть міри довжини.

- Що ми обчислювали на минулому уроці, використовуючи лінійні міри? (Периметр)

- Що вивчали на минулому уроці? (Обчислювали площу прямокутника)

- Як обчислити площу прямокутника?  (Щоб  обчислити площу прямокутника, потрібно довжину прямокутника помножити на ширину)

4. Повідомлення теми, мети уроку.

- Сьогодні на уроці ми продовжимо обчислювати площу і ознайомимося із одиницями площі.

- Які квадратні міри використовували для обчислення площі прямокутника? (квадратні сантиметри)

- Як обчислити площу квадрата із стороною 10 см?

- Що ми називаємо квадратом? (Квадрат - це прямокутник, у якого всі сторони рівні)

- Отже, щоб обчислити площу прямокутника, ми довжину

множимо на ширину.

5. Повідомлення нового матеріалу.

- Чи можемо ми так само обчислити і площу квадрата?

- Якщо можемо, то яка ширина нашого квадрата? (Ширина нашого
квадрата 10 см)

Sквад. = 10см х 10см = 100 см²

• 10 см - це лінійна міра? (Це 1 дм)
• Вчитель показує дітям квадрат із стороною 1 дм, роздає дітям
  квадратні дециметри і повідомляє, що площа квадрата із стороною
  1дм, називається квадратним дециметром і скорочено
  позначається 1 кв.дм або 1 дм².
• За допомогою цього квадрата
  можна обчислити площу кришки стола чи площу підвіконника,
  картини... Вчитель показує відрізок довжиною 1 дм і запитує чи є
  різниця між 1 дм і 1 дм²?
• Як ви думаєте, який квадрат нам потрібно використати, щоб
  обчислити площу класу?

Вчитель показує квадрат із стороною 1 м і повідомляє:

Площу квадрата із стороною 1 м називають квадратним метром і скорочено записують 1 кв.м. або 1 м². За допомогою площі такого квадрата обчислюють площу класу, квартири, грядки на городі.

Вчитель показує відрізок довжиною 1 м і запитує чи є різниця між 1 м і 1 м²?

- Площу квадрата із стороною 1 км називають квадратним кілометром і скорочено записують 1 км². Принести такий квадрат в клас і показати неможливо, чому? (За допомогою такого квадрата обчислюють площу міст, областей, країн, материків, тобто велику площу).

- Із квадратом площа якого 1 см² ви знайомі.

На міліметровому листі паперу вчитель показує квадрат із стороною 1 мм і повідомляє, що площа квадрата із стороною 1 мм називається квадратним міліметром і скорочено записують 1 кв.мм або 1 мм². За допомогою такого квадрата обчислюють площі маленьких фігур.

Вчитель ставить таблицю 1 перед дітьми і пропонує записати пояснення в зошити.

6. Первинне закріплення нового матеріалу.

Завдання 1. Обчислити площу квадратів, зображених на міліметровому папері.

- Якими мірами скористається для обчислення площі? (Квадратними міліметрами)

- Як обчислити площу такого квадрата? (Виміряти довжину і ширину квадрата у міліметрах і перемножити їх) Працювати з середньою і слабшою групами.

7. Виконання практичної операції.      

Завдання 2. Обчислити площу класу і периметр класу.

- Форму якої фігури має клас? (Форму прямокутника)

- Які міри використаєте для обчислення площі класу? (Квадратні метри)

- Як обчислити площу класу? (Виміряти довжину і ширину класу в метрах і перемножити їх).

- Як обчислити периметр нашого класу? (Додати довжини всіх сторін прямокутника). Виконує основна група. З рештою  працює вчитель.

8. Повторення, узагальнення і систематизація знань учнів.

Завдання 3. Робота з підручником самостійно.

- Скільки стрічки потрібно для оздоблення сторін хустинки,  якщо відомо, що хустинка квадратної форми із довжиною сторони 3 дм. Яку площу займає хустинка?

Основна група працює самостійно. З рештою – вчитель.

9. Домашнє завдання (побудувати квадрат із стороною 8 см і обчислити  площу та периметр)

10. Підведення підсумків уроку.

- Якими мірами вимірюємо периметр?

- Якими мірами вимірюємо площу?

- Назвіть одиниці площі, покажіть 1мм²  ,    1см² , 1дм² .

- Чим відрізняється 1 дм від 1дм^{2 ,}       1м від 1м²?  

- Площу якої фігури навчилися обчислювати на уроці?

Оцінювання навчальних досягнень учнів.

 

Тема уроку: Розв'язування задач на обчислення площі прямокутника, квадрата.

Мета:

- систематизувати і узагальнити знання учнів про вимірювання і 

обчислення площі прямокутника, квадрата;

- сприяти розвитку практичних умінь розв’язування задач;

- вчити виділяти суттєві ознаки фігур;

- розвивати просторову уяву учнів, дрібну моторику пальців рук, окомір.

Обладнання: таблиці мір довжини, площі, моделі геометричних фігур.

Хід уроку.

1.  Організація учнів на урок.

Зосередити увагу учнів. Перевірити наявність робочого приладдя.

Нервово-психологічна підготовка учнів до уроку.

Вчитель пропонує серед моделей многокутників спочатку вибрати чотирикутники і пояснити, як діти це зробили. Потім серед чотирикутників вибрати тільки ті, у яких протилежні сторони паралельні. Запитує учнів: «Як називають такі чотирикутники?» (Паралелограмами)

Серед паралелограмів вибрати спочатку прямокутники, а вже з прямокутників - квадрати.

2. Перевірка домашнього завдання.
3. Актуалізація опорних знань учнів.

- Що ми вивчаємо на уроці геометрії?

- Які лінії вивчаємо?

- В яких мірах вимірюємо відрізки?

- Назвіть і покажіть лінійні міри.

- Які многокутники вивчаємо на уроках геометрії?

- Що називаємо сумою довжин сторін многокутника?

- Які міри використовуємо для обчислення периметра?

- Яку ще відому для вас величину ви можете обчислити? (Площу)

- Площу яких фігур ви можете виміряти, використовуючи палетку?

- Площу яких фігур ви можете обчислити за формулою?

4. Виконання практичної операції.

Вчитель дає завдання:

- Обчисліть площу вказаного прямокутника на око. А точність обчислення перевірте шляхом вимірювання і обчислення.

- Що потрібно знати для обчислення площі прямокутника? (Довжину прямокутника і ширину)

- Як обчислити площу прямокутника?  (Щоб  обчислити площу прямокутника потрібно довжину прямокутника помножити на ширину)

- Якими одиницями площі скористаєтесь для обчислення площі? (квадратними сантиметрами)

Учні на око вимірюють площу прямокутника, вчитель записує відповідь кожного учня на дошці.

Тоді 1 учень проводить вимірювання сторін прямокутника і обчислює площу. Учня, який провів найближче обчислення площі, вчитель оцінює найвищим балом.

5. Повторення, узагальнення і систематизація знань учнів по заданій темі (вміння обчислювати площі прямокутника, квадрата)

а)  Довжина залу 12 м, а ширина на 2 м менша. Чому дорівнює площа залу?

б) Площа спортзалу  120 м²,  ширина 6  м. Чому дорівнює довжина
спортзалу?

в) Основній групі вчитель дає самостійне завдання по картках типу:
     1) Обчислити площу кожного прямокутника.

2) Знайти ширину прямокутника.

Площа	Довжина	Ширина
40 см2	8 см	?
250 м2	25м	?
600 м2	30 м	?
120 см2	20 см	?
48 см2	8 см	?
420 дм2	70 дм	?

 

Із слабшою групою вчитель працює окремо.

Робота з підручником.

Розв’яжіть задачу.

Довжина сараю 80 дм, ширина – 60 дм. Дрова займають усієї площі, на решті площі лежить цегла. Скільки квадратних дециметрів площі зайнято під цеглу?

(Учні читають умову задачі. Вчитель проводить аналіз.)

- Про що йде мова в задачі?

- Про що питає задача?

- Що говориться в задачі про цеглу?

- Що означає знайти решту?

- Як знайти решту?

- Яких даних не вистачає, щоб знайти решту?

- Як знайти усієї площі?

- Як обчислити площу сараю?

(Sсараю = 80дм х 60дм = 4800 дм²

4800 дм²: 4 х 3 = 3600 дм²   - займають дрова                                                                                            

- 4800 дм² - 3600 дм²  = 1200 дм²  площі зайнято під цеглу).

6. Домашнє завдання.

- Знайдіть довжину прямокутника, у якого площа – 560 дм², а ширина –

70 см.

7. Підведення підсумків уроку.

Оцінювання навчальних досягнень учнів.

 

Рекомендована література

1.   Демидова М.Е. Работа с геометрическим материалом в школе VIII вида // Дефектология. - 2002. - №1. - С.51-60.
2.   Липа В.О. Організаційно-методичні умови поліпшення стану корекційної роботи в спеціальній школі. Дидактичні та соціально-психологічні аспекти корекційної роботи у спеціальній школі: Наук.- метод, зб.: Вип. 4 // За ред. В.І. Бондаря, В.В. Засенка. - К.: Знання, 2002. -С. 156-159.
3.   Миронова С.П. Підготовка вчителів до корекційної роботи в системі освіти дітей з вадами інтелекту: Монографія. - Кам'янець - Подільський: Аксіома, 2007. - 205 с.

5.   Перова М.Н., Эк В.В. Изучение взаимного положения геометрических фигур на плоскости на уроках математики во вспомогательной школе// Дефектология. - 1982. - №1. - С.29-36.

6.   Перова М.Н., Эк В.В. Обучение наглядной геометрии во вспомогательной школе. - М.: Просвещение, 1983
7.   Попович С.М. Состояние знаний учащихся вспомогательной школы о существенных признаках геометрических фигур // Дефектология. - 1982. - №6. - С.33-36.
8.   Попович С.М. Шляхи вивчення геометричних фігур в допоміжній школі методичний лист / За ред. Г.М.Мерсіянової - К.: Радянська школа, 1967. -46с.
9.   Тишин П.Г. Обучение учащихся вспомогательной школы наглядной геометрии // Известия АПН РСФСР. - 1952. - Вып. 41. -С.79-164.