Множини комбінаторики

 

 

 

 

«Завдання з комбінаторики для самостійних робіт»

(з алгоритмами розв’язування задач)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пояснювальна записка

Дана підбірка завдань охоплює повний курс комбінаторики 11 класу та супроводжується достатньою кількістю детально розв’язаних задач та прикладів.

Значну кількість задач і вправ подано для самостійної роботи учнів за рівнями складності. Вони можуть слугувати для тематичних контрольних робіт, тематичного оцінювання навчальних досягнень учнів чи багатоваріантних індивідуальних завдань.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Планування розділу «Комбінаторика»

«Алгебра та початки аналізу» – 11клас

Елементи комбінаторики (8 годин)

Програмові вимоги до рівня загальноосвітньої підготовки учнів	№ уроку	Тема уроку	Мета уроку
Мають уявлення про: • множину та її елементи; • порожню множину; • способи задання множин; • підмножину поданої множини. Знають означення: • об'єднання, перерізу, різниці множин; • доповнення множини; • перестановки, розміщення та комбінації. Знають формули для обчислення числа перестановок, розміщень і комбінацій.	1	Множина та її елементи. [Числові множини. Множина комплексних чисел.] Способи задання множин	Сформувати поняття множини та її елементів, порожньої множини; ознайомити з видами множин; домогтися засвоєння способів задання множин
	2	Об'єднання та переріз множин. Віднімання та доповнення множин	Сформувати поняття об'єднання, перерізу, різниці множин, доповнення множини; сформувати вміння знаходити об'єднання, переріз, різницю множин і допов- нення множини
	3	Упорядкована множина. Перестановки	Сформувати поняття упорядкованої множини, перестановки; домогтися засвоєння формули для обчислення числа перестановок
	4	Розміщення	Сформувати поняття розміщення; домогтися засвоєння формули для обчислення числа розміщень
Вміють: •знаходити об'єднання, переріз, різницю множин, доповнення множини; •розрізняти види сполук і знаходити їх число за відповідними формулами; •розв'язувати комбінаторні задачі	5	Комбінації	Сформувати поняття комбінації; домогтися засвоєння формули для обчислення числа комбінацій та властивостей комбінацій
	6	Біном Ньютона	Домогтися засвоєння формули бінома Ньютона, властивостей бінома Ньютона; сформувати вміння знаходити п-й член розкладання бінома Ньютона
	7	Розв'язування прикладних за­дач	Сформувати вміння розрізняти види сполук; удосконалити вміння розв'язувати комбінаторні задачі, в тому числі прикладного характеру
	8	Контрольна робота	Перевірити рівень засвоєння знань із теми «Елементи комбінаторики »

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок №1.

 Множина та її елементи. [Числові множини. Множина комплексних чисел.] Способи задання множин.

Зразки розв’язування завдань

1.          Опишіть множину натуральних чисел.

Розв'язання

Одиниця є найменшим натуральним числом. Кожне наступне натуральне число на одиницю більше від попереднього. Якщо множина натуральних чисел М містить одиницю і разом з будь-яким натуральним числом п містить число п + 1, то до множини М належать усі натуральні числа, тобто М=N.

Цими властивостями описується натуральний ряд чисел. Вони є характеристичними властивостями множини натуральних чисел.

Узагалі, множина може визначатися заданням характеристичної властивості її елементів, тобто такої властивості, яку мають усі елементи цієї множини, і тільки вони.

Розв'язання

Такою властивістю є подільність кожного числа на 2, адже, за означенням, парним називають число, яке ділиться на 2, і навпаки - всяке парне число ділиться на 2. Парне число позначають 2k, k є Z. Множину парних чисел можна записати Z₂= {п,п = 2k, kєZ}.

3. Запишіть усі множини чисел, рівні множині {1; 2; 3}.
Розв'язання

Множинами, рівними до множини {1; 2; 3}, будуть: {1; 3; 2}, {2; 1; 3}, {2;3;1},{3;1;2},{3;2;1}.

4. Покажіть, що множина раціональних чисел є упорядкованою.
Розв'язання

Кажуть, що раціональне число р передує раціональному числу q, якщо р менше q (р < q). Тоді на множині раціональних чисел виконуються властивості відношення порядку: із двох раціональних чисел має місце лише одне із співвідношень; р = q, або р < q, або q <р. Для довільних трьох раціональних чисел р, q, r з того, що р < q і q < r, випливає, що р < r. Отже, множина раціональних чисел є впорядкованою.

5. Запишіть множину коренів многочлена х⁴ - 2х³ - 13х² + 14х + 24.
Розв'язання.

Даний многочлен можна записати так: х⁴ - 2х³ - 13х² + 14х + 24 = (х⁴ - х³ -

• 12х²) + (-х³ + х² + 12х) + (-2х² + 2х + 24) = х²(х² - х - 12) - х(х² - х - 12) - 2(х² - х -
• 12) = (х² - х - 12)(х² - х - 2) = (х + 3)(х + 1)(х - 2)(х - 4).

Отже, множина коренів многочлена - {-3, -1,2,4}.

Завдання для самостійного розв'язування.

Група А

1. Наведіть приклади множин з навколишнього життя, виробничої діяльності, природничих наук тощо. Для кожної з наведених множин утворіть підмножини.
2. Наведіть приклади відомих вам множин з математики (алгебри, геометрії). Для кожної множини знайдіть кілька підмножин.

3. Складіть перелік усіх символічних позначень, які трапляються у вивченій темі.
4. Знайдіть усі підмножини таких множин: а) М= {а, b, с}; б) S= {d, е,f,k};

в)Д = {1,2,3,4}; г)T={Δ,Ο,□}.

5. Знайдіть кілька підмножин множини усіх трикутників площини.
6. Нехай D - множина всіх непарних чисел. Що є характеристичною властивістю елементів цієї множини, як це можна записати? (D= {х, х= 2k+ 1, kєZ}.)

Для яких з наведених пар множин має місце одне зі співвідношень А В,

В  А, А = В: а) А= {а, b, с, d}, В= {а, с, d}; б) А = Ǿ, В = Ǿ; в) А = Ǿ, В= {а, b, с};г)А = {а, b, с},В= {b, с, а}? (а) B   А; 6)А = В; в) А    В; г)А = В.)

Група Б

8. За даною характеристичною властивістю елементів множини запишіть множину, перерахувавши її елементи: а) додатні числа, кратні 5, які розміщені в інтервалі (20; 80); б) усі цілі невід'ємні числа, менші від остачі від ділення числа 76 на 31.
9. Нехай А - множина, що складається з 8 учнів класу, які відвідують гурток з математики, а В - множина всіх учнів даного класу. Чи рівні ці множини?

 

10. Нехай N — множина натуральних чисел. Запишіть символічно підмножину М усіх натуральних чисел, кратних 3. (М= {х, х=3к, к є N}.)
11. Пряма р є серединним перпендикуляром (медіатрисою) відрізка АВ. Вкажіть характеристичну властивість множини точок прямої p.

Група В

12. Запишіть множину, елементами якої є розв'язки рівняння х³ -4х -31х+70 = 0. ({-5,2,7}.)
13. Задані множини А = {{а, b}, {с, d}, с, d} та В = {{а, b}, с). Чи пов'язані ці множини між собою? (Так, В 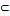    А.)
14. Нехай А= {{1, 2, 3}, {1, 3}, 1, 2}. Чи справедливо, що: а) {1, 2} 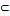   А; б) {1, 2}є А; в) {1, 3} є А; г) {1, 3}  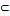 A? (а) Так; б) ні, тому що серед елементів множини А немає елемента {1, 2}; в) так; г) так.)

 

 

 

 

 

 

 

 

 

 

 

 

Урок №2. Об'єднання та переріз множин. Віднімання та доповнення множин

Зразки розв’язування завдань

 

Завдання для самостійного розв'язування.

Група А

1.     Вибравши для задоної множини А універсальну множину, вкажіть

Урок №3. Упорядкована множина. Перестановки

Зразки розв’язування завдань

Завдання для самостійного розв'язування.

 

 

 

Урок № 4-5. Розміщення. Комбінації

Зразки розв’язування завдань

 Завдання для самостійного розв'язування.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок №6. Біном Ньютона

Зразки розв’язування завдань

 

  

 

 

Завдання для самостійного розв'язування.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок №7-8. Розв'язування комбінаторних за­дач і вправ

 

Зразки розв’язування завдань

 

 

 

 

 

 

  

Завдання для самостійного розв'язування

 

 

 

Завдання для контрольної роботи

Додаток 1

Основні властивості сполук

 

 

 

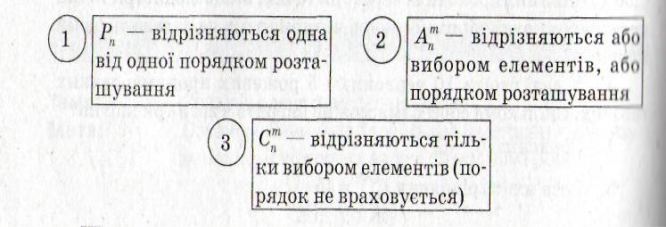
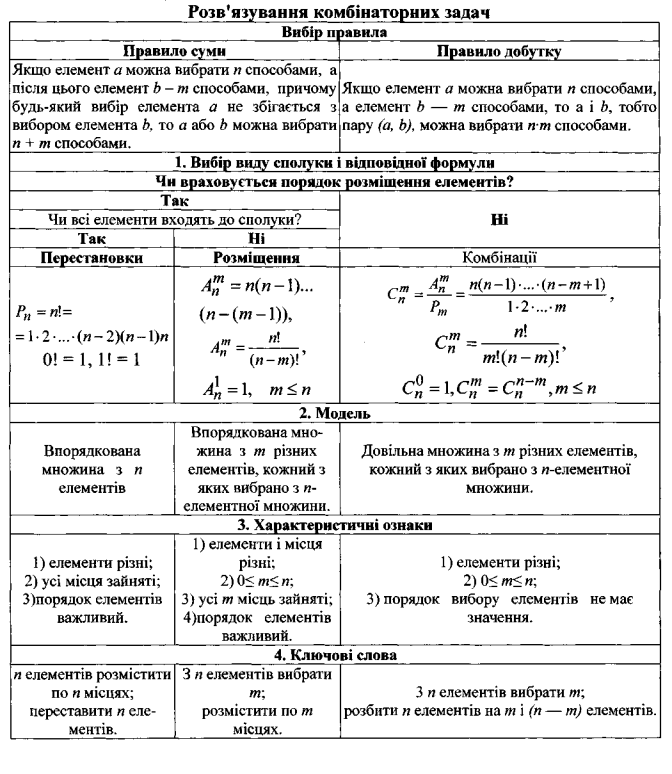
Вибір формули

 

 

 

 

 

 

 

 

 

 

Додаток 2

 

 

 

 

 

ЛІТЕРАТУРА

1.          Авраменко М. І. Уроки алгебри і початків аналізу в 10 і 11 класах: Посібник для вчителя. — К.: Рад. пік., 1989. — 320 с.
2.          Алгебра і початки аналізу: Навчальний посібник для 9-го класу середньої школи/за редакцією А. М. Колмогорова. — К.: Рад. шк., 1976. — 263 с.
3.          Бевз Г. П. Алгебра 7-9. — К.: Освіта, 1996. — 303 с.
4.          Бродський Я., Павлов О. Про викладання елементів теорії ймовірностей в школі//Математика. — №№ 23-24 (83-84), 2000.
5.          Бугір М. К. Теорія ймовірностей та математична статистика. — Тернопіль: Підручники і посібники, 1998. — 176 с.
6.          Бушмакін В. М. та ін. Комбінаторика: Навчальний посібник /Серія «Математика для інженерів», №8. — Львів: Львівська Політехніка, 2002. — 196 с.
7.          Вікторова Н. В. Початки теорії ймовірностей//Математика. — №3-7 (159-163), 2002.
8.          Війчук Т. І., Хмара Т. М. Елементи математичної статистики в середніх загальноосвітніх закладах: Посібник для вчителів та учнів класів фізико-математичного профілю. — Дрогобич: Каменяр, 2003. — 92 с.
9.          Глейзер Г. И. История математики в школе. ІХ-Х классьі: Пособие для учителей. — М.: Просвещение, 1983 — 350 с.
10.     Завало С. Т. Арифметика, алгебра і елементи аналізу. — К.: Рад. шк., 1969.—503 с.
11.     Збірник задач з математики для вступників до вузів/за ред. М. І. Сканаві. — К.: Вища школа, 1992. — 445 с.
12.     Істер О. С. Комбінаторика, біном Ньютона та теорія ймовірностей. — Харків: Гімназія, 1999. — 184 с.
13.     Кисельов А. П. Алгебра, ч. II. Підручник для середньої школи. — К.: Рад. школа, 1964. — 263 с.
14.     Ляпин С. Є., Баранова И. В., Борчугова 3. Г. Сборник задач по злемен-тарной алгебре. — М.: Просвещение, 1973. — 350 с.
15.     Павлова Л. В., Дітчук Р. Л., Коваль Г. П. Початки теорії ймовірностей. Навчально-методичний посібник. — Дрогобич: Каменяр. — 2003. — 118 с.
16.     Погорєлов О. В. Геометрія: Навчальний посібник для 6-10 класів середньої школи. — К.: Рад, школа, 1985 —271 с.
17.     Процай В. Ф., Новикова У. В. Комбінаторика і теорія ймовірностей у школі. — Харків: Каравела. — 1997. — 192 с.
18.     Скобелев Г. М. Елементи сучасної математики. — К.: Вища школа, 1971. —65 с.
19.     Шкіль М. І., Слєпкань 3.1., Дубинчук О. С. Алгебра і початки аналізу: Підручник для 11 класу загальноосвітніх навчальних закладів. — К.: Зодіак-Еко. — 2002. — 383 с.