ДЕПАРТАМЕНТ ОСВІТИ ВІННИЦЬКОЇ МІСЬКОЇ РАДИ

КУ «МІСЬКИЙ МЕТОДИЧНИЙ КАБІНЕТ»

КЗ «ЗАГАЛЬНООСВІТНЯ ШКОЛА  I-III СТУПЕНІВ №10

ВІННИЦЬКОЇ МІСЬКОЇ РАДИ»

 

 

 

 

 

 

Наочне приладдя

 при вивченні математики в школі

 

номінація «Навчально-методичний посібник»

 

 

 

Найко Володимир Антонович вчитель математики, спеціаліст 

вищої кваліфікаційної категорії, 

старший учитель тел. (098) 354 09 32

 

 

 

 

 

Вінниця 2017

 

Автор Найко Володимир Антонович, вчитель математики комунального закладу «Загальноосвітня школа I-III ступенів №10 Вінницької міської ради»

 

 

Найко В.А. Наочне приладдя при вивченні математики в школі Методичний  посібник/В. А. Найко. - Вінниця: ММК, 2017. 42 с.

 

 

Рецензенти:

Максименюк Олена Михайлівна, заступник директора з навчально – виховної роботи,спеціаліст вищої кваліфікаційної категорії , вчитель методист 

Франчук Галина Іванівна, учитель математики комунального закладу «Загальноосвітня школа I-III ступенів №10 Вінницької міської ради», спеціаліст вищої кваліфікаційної категорії, вчитель-методист 

 

 

Рекомендовано методичною радою  комунального закладу «Загальноосвітня  школа I-III ступенів №10 Вінницької міської ради»

(Протокол №  5 від  23.01.2017р.)

 

У даному посібнику розглядається специфіка використання наочного приладдя на уроках математики.

Актуальність роботи полягає в тому, що виготовлене обладнання дозволяє доступно викласти навчальний матеріал, висвітлити первинні поняття тієї чи іншої теми.

Розробка складається із двох частин. В першій частині приведено опис приладів, їх будова та специфіка використання. У другій частині розглядається характер роботи із обладнанням на уроках  при вивченні певних математичних понять . 

У роботі приведено приклад міжпредметних зв’язків: доведення математичної теореми на основі термінів та понять фізики.

ЗМІСТ

 

ВСТУП……………………………………………………………………..          4

РОЗДІЛ І. ПРИЛАДИ ДЛЯ ВИВЧЕННЯ  МАТЕМАТИЧНИХ                  

ПОНЯТЬ…………………………………………………………................          6

          1.1. Модель тригонометричного кола………………………….........        6

          1.2. Похідна……………………………………………………………       9

          1.3. Площі многокутників…….……………………………………...        13

          1.4. Функція. Властивості функції…………………………………..        16

          1.5. Метод інтервалів……………………………………………........        18

          1.6. Інтеграл…………………………………………………….……..        23

РОЗДІЛ ІІ.  ЗАСТОСУВАННЯ ПРИЛАДІВ НА УРОКАХ       МАТЕМАТИКИ ТА В ПОЗАКЛАСНІЙ РОБОТІ……………………         25

          2.1. Засідання математичного гуртка  «Властивість точки                     

                             перетину медіан трикутника»......................................................        25

           2.2. Урок «Розв’язування нерівностей методом інтервалів»………     27

          2.3. Урок «Означення тригонометричних функцій довільного               

                             кута»………………………………………………………………        31

          2.4. Урок « Площа трикутника»………..…………………………….       36

ВИСНОВОК………………………………………………………………...  41

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ……………………………….         42

ВСТУП

 

З розвитком науки, культури  й техніки значення математики зростає як в науково-практичній діяльності людства, так і в навчанні та вихованні молоді. Значення математики як науки й навчального предмета підкреслювали генії людства. «Ніякі людські дослідження на можна назвати справжньою наукою, якщо вони не пройшли через математичні доведення», - говорив Леонардо да

Вінчі. 

Виникає потреба розвинути  в учнів не тільки тверді навички використання математичних знань, але й сформувати в них уявлення про основні поняття, ідеї та методи математичної науки, максимально впливати на їх загальний розвиток. Все це спрямовує на пошук таких методик і засобів навчання, які дозволяють добитися оптимального рівня математичних знань.

 Відомо, що математика виникла й розвивалась завдяки потребам людства. Виявляється й навпаки: для розв’язання математичної  проблеми є досить ефективним прийом переведення її розв’язання в практичну «площину».  Тому важливим напрямом  вивчення математики є використання навчального обладнання вчителем як на уроках, так і в позаурочний час. Метою даної роботи є узагальнення практичного досвіду виготовлення та використання наочного приладдя на уроках математики та заняттях математичного гуртка.

На сьогодні відчувається загальне послаблення інтересу учнів до вивчення математики. Однією з причин є факт відірваності математики від життя. Сучасні тенденції розвитку шкільної математики у світі спрямовані на прикладне застосування математичних знань. Саме тому даний посібник є актуальним та своєчасним. Матеріали, що розміщені в  посібнику, дають змогу глибше зрозуміти  не лише фундаментальні поняття математики,  а й реалізацію набутих знань на практиці. Це відповідає новому Держстандарту (2011 р.) щодо ключових та предметних компетентностей учнів [1].

Ідея розробки та виготовлення навчального обладнання виникає у зв’язку з потребою викласти  те чи інше поняття більш доступно, зрозуміло, розкрити його динаміку, показати його місце у вивченні даної теми. Характерною особливістю виготовленого навчального обладнання є те, що прилади в основному висвітлюють первинні поняття тієї чи іншої теми. На цьому етапі важливим є психологічне налаштування учнів. Тому необхідно розкрити поняття в найбільш  доступній формі. Бажано показати місце, важливість, застосування того чи іншого  математичного поняття. Учні повинні відчути себе повноправними учасниками дослідницького, творчого процесу на уроці.  Наприклад, на уроці відбувається перше знайомство  із похідною, означення якої є досить абстрактним і далеким від розуміння учнями. Тому необхідно показати, що відношення  характеризує поведінку функції. За означення 

, тоді при функція зростає, функція спадає, =0 функція стала. Тобто розкрито основну «місію» похідної - дослідження функції.

Ще одним напрямком при роботі з приладами є ідея вивчення навчального матеріалу в цілому, в комплексі, у взаємозв’язку .  Це чітко видно при опрацюванні теми  «Площі фігур».   

Важливе місце при вивченні математики займають нерівності. Розв’язування нерівностей методом інтервалів посідає ключове місце, оскільки цей метод є універсальним.  Прилад, за допомогою якого вивчається метод інтервалів, дозволяє більш доступно показати тонкощі розв’язування нерівностей, зрозуміти причини та динаміку зміни знаків. Використання приладу дає змогу більш свідомо, глибоко засвоїти дану тему.

Разом з тим при використанні навчального обладнання необхідно враховувати багато різних факторів: специфіку даного класу, загальний рівень підготовки учнів тощо.

           

РОЗДІЛ І. ПРИЛАДИ ДЛЯ ВИВЧЕННЯ МАТЕМАТИЧНИХ ПОНЯТЬ

 

1.1. Модель тригонометричного кола

Ввивчення теми  «Тригонометрія» в середній школі пов’язано з певними труднощами, зокрема високим рівнем абстракції понять, складної логічної структури їх означень. Тому головною метою вчителя є застосування таких методів і засобів навчання, які б сприяли викладу матеріалу  більш доступно, образно,  динамічно та результативно, що в свою чергу дозволятиме учням легше сприймати, усвідомлювати та більш глибоко розуміти навчальний матеріал. Необхідно відмітити, що курс тригонометрії основної школи продовжує мати велику практичну направленість, що вимагає від учнів ґрунтовного оволодіння основними поняттями, умінням  виконувати різного роду перетворення виразів, дослідження функції та побудови графіків тощо. Причому, вивчення понять тригонометрії  не обмежується  рамками вивчення одного предмета. Школярі повинні мати ґрунтовні знання з названої теми, оскільки ці знання є ланкою понять у довгому ланцюгу й мають велике значення в реалізації міжпредметних зв’язків.

Будова приладу 

 

 

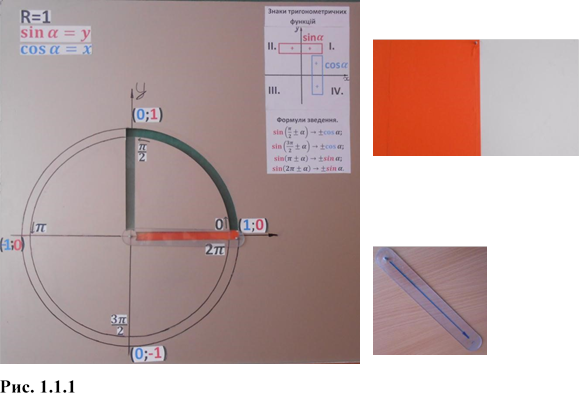
Корпус виготовлений із пластику, покритого металом. На корпусі зображена система координат та тригонометричне коло. Частина  осей координат та кола вирізані. Вирізана частина осі абсцис та ординат із тильної сторони корпусу скріплює органічне скло,  наклеєне на корпус (Рис. 1.1.1).

Радіус-вектор - органічне скло з двома отворами. Його вісь обертання - центр кола.  До іншого отвору кріпиться екран. Екран знаходиться за корпусом.

Екран виготовлено із пластику. У верхній частині екрана є отвір, яким він кріпиться до радіус–вектора, це і є вісь обертання екрана. Довжина екрана дорівнює діаметру кола  і завжди  паралельна лінії горизонту, оскільки отвір на екрані ділить довжину навпіл.  Ширина екрана дорівнює радіусу кола.

   

Застосування

8                    клас. Вивчаючи означення тригонометричних функцій гострого кута, доречно провести демонстрацію того факту, що при зростанні гострого кута синус та тангенс зростають, а косинус, котангенс спадають. Зокрема,  учні одержують досить важливі знання щодо зростання, спадання функцій як в цілому, так і в конкретному прикладі.

9                    клас. При вивченні елементів тригонометрії  в 9 класі обґрунтування того, що , . При цьому потрібно виконати нескладні побудови в 2 чт, які будуть симетричні малюнку в I чт. відносно осі ординат.

10               клас. Навчальний матеріал розділу  «Тригонометричні функції», що вивчається в курсі «Алгебра та  початки аналізу» (10 клас), є досить великим за обсягом, це вимагає додаткових наочно - демонстраційних засобів навчання.  

Тому найбільш ефективно та широко можна застосовувати можливості наочності приладу в роботі з учнями 10 класу. Насамперед учні повинні засвоїти, що синус та косинус кута - це координати відповідної точки

одиничного кола, тобто  звідки .  В подальшому  встановлюємо значення  тригонометричних   функцій,  якщо

 і т. д.  (Рис. 1.1.2 – Рис. 1.1.5).

Заслуговує уваги означення синуса та косинуса довільного кута як  відповідні проекції радіус-вектора на координатні осі. (Потрібно зауважити, при цьому, що наведені означення ідентичні).    Використовуючи такий підхід

 

Рис. 1.1.2                                                  Рис. 1.1.3

 

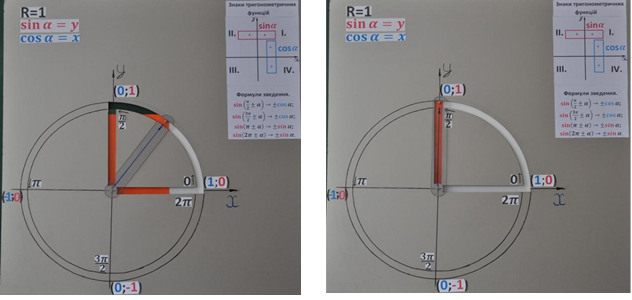
Рис. 1.1.4                                                  Рис. 1.1.5

щодо означення тригонометричних функцій, учні краще розуміють явище  монотонності функцій. Це виконуємо за допомогою приладу в I чверті. Відповідно моделюємо процес монотонності функцій в інших чвертях.  

Досить легко знаходимо, що для функцій у= та у= область значень 1 і Т=Схематично побудуємо графік функцій.

Таблиця,  яка зображена на рис. 1.1.2, дає можливість легко запам’ятати  або встановити знаки тригонометричних функцій в будь-якій чверті. Наведені приклади щодо формул зведення для функції у=показують закони зміни функції на «кофункцію» або закон коли дана функція залишається. Аналогічні принципи для  функцій у=  у=tgx, y=ctgx.

 

1.2  Похідна

Поняття похідної – фундаментальне поняття математичного аналізу, за допомогою якого досліджують явища в природничих, соціальних і економічних науках. Тому в шкільному курсі розділу алгебри та початків аналізу «Похідна та її застосування» займає значне місце. Це пов’язано із широким застосуванням цих понять як у шкільній математиці, так і у фізиці. 

При вивченні теми «Похідна» з’являються певні труднощі, пов’язані із здійсненням граничних переходів. Тому важливо надати вивченню теми більш наочний і конкретний характер.  

 

Будова приладу

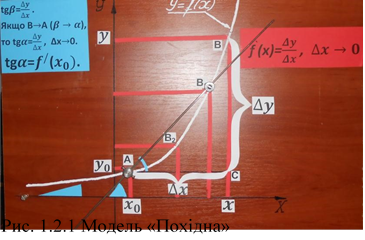 На    корпусі       зображено прямокутну систему координат та     графік         функції.          Також нанесені побудови необхідні для означення похідної. В точках В, В_1, В₂ знаходяться магніти.  Металевий стержень (січна) має вісь обертання в точці А. На

металевому стержні  є повзунок, який знаходиться (Рис. 1.2.1) в точці В_1. Його найнижче місце-в точці А, тоді металевий стержень займає положення дотичної (Рис. 1.2.5). Зліва в нижньому куті знаходиться фіксатор крайнього положення стержня.

Застосування

Означення січної, дотичної. Обговорення зв’язку між січною та дотичною. Розглянути динаміку наближення січної до дотичної в т. А (Рис.

1.2.2 – Рис. 1.2.5).

 

Миттєва швидкість

Нехай тіло рухається по траєкторії графіка функції. Визначимо миттєву швидкість руху тіла, коли швидкість змінюється як по модулю, так і за напрямом (Рис. 1.2.2 - Рис.1.2.5).

Рис. 1.2.2                                                                                    Рис. 1.2.3

                 

Рис. 1.2.4                                                   Рис. 1.2.5

а)  , якщо В     (

б)   , якщо .

в)   , якщо , і т. д.

Найближчим значення миттєвої швидкості є середня швидкість в третьому випадку. 

Отже .

Таким чином, для визначення миттєвої швидкості руху тіла в деякій точці потрібно виміряти переміщення за такий проміжок часу, за який можна вважати швидкість практично незмінною. Розглянувши поняття похідної, узагальнюючи, маємо . Оскільки прискорення характеризує швидкість зміни швидкості  а=

Означення похідної. Похідна – основне поняття диференціального

 

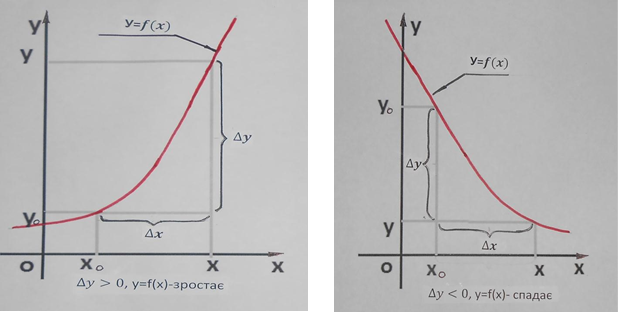
Рис. 1.2.6                                                                 Рис. 1.2.7

 

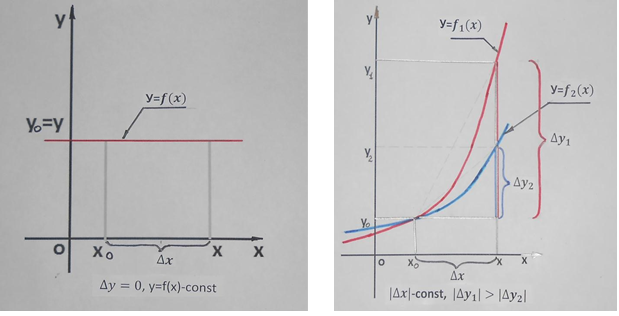
Рис. 1.2.8                                                                 Рис. 1.2.9

числення, що характеризує швидкість зміни функції та інші її властивості.

Нехай і y= y- Тоді основною характеристикою поведінки функції в точці є відношення. Наприклад. За означенням . Звідси головним фактором виступає приріст функції . Якщо 0, тоді функція зростає,  функція стала. Якщо - const і

 тоді перша функція швидше змінює своє значення, ніж інша.

За означенням, похідною функції у=в точці називають границю відношення приросту функції до приросту її аргументу, коли приріст аргументу

прямує до нуля (коли така границя існує). Тому –

Рис. 1.2.9).

Геометричний зміст похідної

Із трикутника АВС, кут С- прямий, маємо tgA , тобто tg. Якщо

т.Вт.А значить 0 тоді . Таким чином   

(Рис. 1.2.2 - Рис. 1.2.5).

Отже, похідна функції y= в точці  дорівнює тангенсу кута нахилу дотичної до графіка функції в точці  із додатнім напрямом осі абсцис.

 

Рівняння дотичної

Рівняння дотичної тісно зв’язане з її кутовим коефіцієнтом. Складемо рівняння дотичної (прямої), яка проходить через точку А із кутовим коефіцієнтом  k==). Рівняння прямої має вигляд  y=k, тобто  у=  (1)  Знайдемо значення b. ( Рис. 1.2.5 )

Оскільки дотична проходить через точку ( її координати задовольняють рівняння. Отже,  +b, звідки b =-    (2)

Із (1) і (2) маємо у=+- ;   

у-=- ;

у-=( – рівняння дотичної.

 

 

 

 

 

1.3.   Площі многокутників

Тема  «Площа» є базовою, фундаментальною і вивчається на протягом усього курсу математики, починаючи із 5-6 класів. Засвоєння ж учнями названої теми викликає певні труднощі. При цьому важливо, щоб кожен із учнів зрозумів поняття, визначення при першому знайомстві. Таким чином, виникає потреба  ефективних методів, засобів вивчення елементів геометрії. Одним із підходів ефективного вивчення площ геометричних фігур є вивчення їх в комплексі, у взаємозв’язку між ними. При цьому необхідно також враховувати, що багато учнів не сприймають навчальний матеріал, якщо викладені факти розглянуто на недостатньо обґрунтованому  рівні, який їм  доступний. 

 

Висота в тупокутному трикутнику

На відміну від гострокутного трикутника проведення висот в тупокутному трикутнику викликає в учнів певні труднощі. Тому можна запропонувати провести висоти в тупокутному трикутнику, використовуючи тягарець. В подальшому учні більш простіше оцінюють завдання проведення висот в тупокутному трикутнику (Рис. 1.3.1, Рис. 1.3.2).   

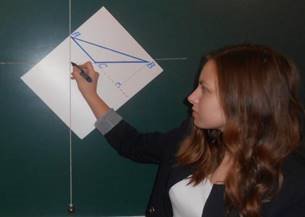
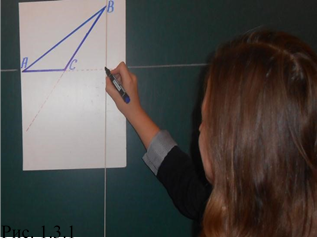Рис. 1.3.2

Площа паралелограма

Розглянемо паралелограм із стороною а та висотою h. Виконавши перетворення паралелограма в прямокутник, одержимо S_парал.=S_прмок. S_прям.=аh,де а,h- сторони прямокутника. Отже, S_парал=аh, де а-сторона паралелограма,     h- висота паралелограма, проведена до цієї сторони (Рис.1.3.3, Рис. 1.3.4).

 

Рис. 1.3.3                                                                                          Рис. 1.3.4

 

Площа трикутника

Нехай маємо паралелограм, площа якого дорівнює S=ah, де а-сторона  прямокутника, h-висота паралелограма. Діагональ паралелограма ділить його на два рівні трикутники. Отже, площа трикутника дорівнює Sah, де а-сторона трикутника, h- висота трикутника (Рис. 1.3.5, Рис 1.3.6).

 

Рис. 1.3.5                                                Рис. 1.3.6

 

Площа прямокутного трикутника

Площа прямокутника дорівнює добутку двох його сторін, тобто S=a b,   a,b- сторони прямокутника. Тоді площа прямокутного трикутника Sa b, де а,в- катети прямокутного трикутника (Рис. 1.3.7, Рис.1.3.8).

 

Рис. 1.3.7                                                   Рис. 1.3.8

Одна із умов рівності площі трикутників

Використовуючи термін «смуги», можна розглянути дещо інший підхід  до традиційного визначення площі фігур. Наприклад, щоб обчислити площу паралелограма, можна довжину будь-якої із його  паралельних сторін помножити на ширину смуги, якій належать ці сторони. Виходячи із цих міркувань, площа трикутника дорівнює половині добутку сторони трикутника  на ширину смуги двох паралельних прямих, одна із прямих якої містить сторону трикутника, друга пряма проходить через третю вершину трикутника. Таким чином, якщо основи трикутників співпадають, а їх вершини лежать на прямій, паралельній основі, то площі трикутників рівні.

 

Площа правильного шестикутника

 

                                                                                                             Рис. 1.3.11

Рис. 1.3.10

Для правильного шестикутника R=a, де R- радіус описаного кола, а- сторона правильного шестикутника. Площа правильного трикутника  дорівнює S. Тоді площа правильного шестикутника дорівнює S, тобто S(Рис. 1.3.10, Рис. 1.3.11).

1.4.  Функція. Властивості функції 

Поняття функції є одним із основних в математиці та інших науках.  Воно відіграє важливу роль у пізнанні навколишнього світу. Вивчення функціональної залежності є важливою навчальною метою для учнів, оскільки дозволяє описувати та вивчати різноманітні залежності між реальними  процесами. Тому виникає досить важлива проблема оволодіння найпростішими методами дослідження функцій. Основна мета створення приладу - формування  навичок дослідження функцій.

 

Будова приладу

Корпус приладу виготовлений із пластику. На корпусі нанесена  система координат та графік функції. Осі системи координат та графік функції вирізані, ширина прорізу 10 мм. На систему координат наклеєне  

 

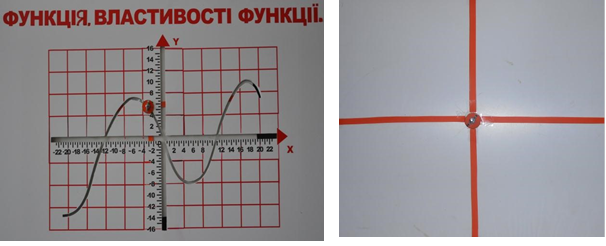
Рис. 1.4.1                                                     Рис. 1.4.2

 

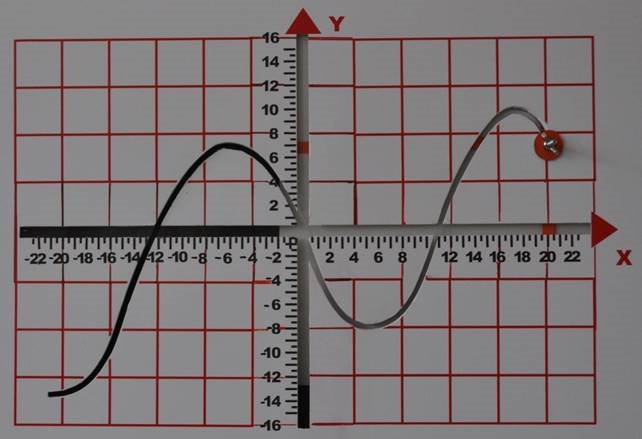
Рис. 1.4.3

 органічне скло. Графік функції прорізаний наскрізь. Екран також із пластику. В центрі екрана зроблено отвір, через який проходять два взаємно  перпендикулярних відрізки. Центр екрана за допомогою болта з’єднаний із шайбою(шайба – точка графіка). Якщо точка (шайба) переміщується відповідно  графіку функції, тоді за допомогою перпендикулярних відрізків встановлюється залежність між відповідними значеннями залежної та незалежної змінної. На задній стінці екрана у двох нижніх кутах знаходяться приклеєні стальні  пластинки, до яких при потребі кріплять магніти. Це дозволяє екрану зберігати задане горизонтальне положення (Рис.1.4.1, Рис.1.4.2). Застосування

6        клас. Вивчення поняття координатної площини. Практична робота зі встановлення координат точок. Графічна залежність між числовими множинами (Рис.1.4.3).

7        клас. Область визначення. Область значень. Практична робота.

Опрацювання визначення графіка функції за допомогою приладу (Рис. 1.4.3).

9                    клас. Повторити область визначення, область значень. Відстеження на приладі  динаміки зростання та спадання функції, проміжків знакосталості.

Знаходження нулів функції (Рис.1.4.3).

10               клас. Повторення навчального матеріалу за 9 клас. Встановлення найбільшого та найменшого значення (Рис.1.4.3).

11               клас. Геометричний зміст похідної та дотична до графіка

(демонстрація).  Визначення найменшого та найбільшого значення (Рис.1.4.3).

 

1.5 . Метод інтервалів

 

Рис. 1.5.1                                                                 Рис. 1.5.2

Метод інтервалів  - спеціальний алгоритм розв’язування нерівностей.

Алгоритм можна поділити на чотири кроки.

а) розв’язати рівняння f(x)=0. Таким чином, потрібно розв’язати рівняння

а не нерівність, що значно простіше.

б) відмітити на координатній прямій всі корені даного рівняння. Тоді

пряма поділиться на кілька інтервалів.

в) Визначити знак (плюс чи мінус) функції у=f(x) на самому правому інтервалі. Для цього достатньо підставити в f(x) будь-яке число, яке буде правіше всіх відмічених коренів.

г) Відмітити знаки на інших інтервалах, оскільки неперервна функція може змінити знак тільки в тих точках, де вона дорівнює нулю.  При цьому можна скористатися методом, вказаним вище, або скористатися закономірностями визначення знаків функції на інтервалах.

Прилад дозволяє більш доступно показати тонкощі розв’язування нерівності методом інтервалів та засвоїти вказані дії на більш високому рівні. Важливо, щоб учні зрозуміли закономірності зміни знаків, неперервної функції  при переході від одного інтервалу до іншого.

 

Будова приладу

 Корпус приладу виготовлений зі склеєних меблевих плит. В пази корпусу (Рис.1.5.2) вставляються пластини. Пластини виготовлені з органічного скла. Кожному лінійному множнику, нерівності  відповідає одна пластина, на якій нанесена числова пряма. На кожній прямій відмічено значення, при якому відповідний  лінійний множник перетворюється в нуль. Червоним кольором виділений проміжок, при всіх значеннях якого  лінійний множник додатній, синім - від’ємний (Рис. 1.5.3,  Рис 1.5.4).

Якщо нерівність складена із трьох лінійних множників, тоді найширшу смугу знаків має пластина, яка знаходиться якнайдалі від учнів. Аналогічно далі (Рис. 1.5.1, Рис. 1.5.5, Рис. 1.5.6).

Застосування. Розв’яжемо нерівність: (х – 2) (х – 3)о (Рис. 1.5.5). Розглянемо функцію    f(x)=( х – 2) (х – 3)0

                    Нулі функції: х=2 або х=3.

   1).  Якщо, то (рис. 1.5.3).

       При всіх  ,  ()  «червоний»

       При всіх  ,       () «синій»

Рис. 1.5.3

   2).   Якщо, то  (рис. 1.5.2).

         При всіх  ,   ()  «червоний»

         При всіх  ,        () «синій»

Рис. 1.5.4   

Нулі функції розбивають числову пряму на інтервали. На  кожному з інтервалів функція зберігає знак. Для даної функції  при переході  через кожен із нулів знак одного із лінійних множників зміниться на протилежний. Тому знак функції також зміниться на протилежний.  Встановимо знак функції  на кожному з інтервалів. 

Рис. 1.5.5

Отже, якщо х(х-2) (х-3) Тоді  f(x) (Рис.1.5.5).

При переході  справа наліво до іншого інтервалу зміниться знак множника 

(х(-) тоді, як (х-2)  їх добуток від’ємний. Таким чином, при умові  2  f(x).  

При умові   (х-2) () і (х-3) () їх добуток  додатній. Значить f(x), якщо   

 

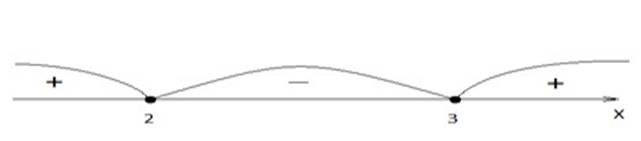
Відповідь. х

2 (Рис. 1.5.6).

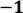
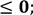Розвязати нерівність:  (х)(х+3)

Нехай f(x)=(х-1)(х 1)(х 3).

Провівши анолігічні міркування до вищезгаданих, маємо:

Рис 1.5.6

1)    х              то х-1,   х 1,   х+3 (+).      f(x)0 (+).

2)    -1х-1,   х 1,  х 3 (+).      f(x)0 (-).

3)    -3, то х-1,   х 1,  х 3 (+).       f(x)0 (+). 4)      то  х-1,    х 1,   х 3 (-)        f(x)0 (-).

Отже, х

Розвязати нерівність: (х+5)²(х+1) (рис. 1.5.7).

Нехай f(x)=(х 5)²(х 1) або f(x)=(х 5) (х 5)(х 1).   

Нулі функції  х=-5 або х=-5 або х=-1

Рис. 1.5.7

1)    х  (х 5) (+),  (х 5), (х 1)  то f(x)0(+).  

2)    -5(х 5) ( ),  (х 5), (х 1)  то f(x)0(-).  

3)    (х 5) (-),   (х 5),  (х 1)  то f(x)0(-).  

Отже, х

 

1.6 .  Інтеграл

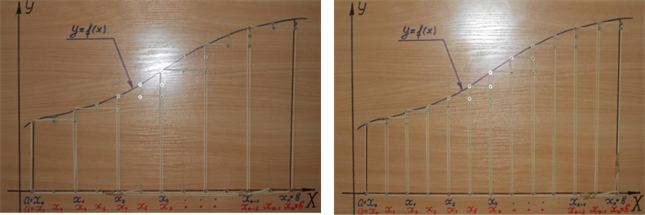
Рис. 1.6.1                                                                                      Рис. 1.6.2

Даний прилад можна застосовувати при вивченні поняття криволінійної трапеції. Особливо ефективно цей прилад можна використовувати при вивченні інтегралу, що є основою розв’язування прикладних задач з математики в школі та у вищих навчальних закладах.

 Інтегралодне із найважливіших понять математичного аналізу. Інтегральне числення, тобто інтеграл, виникло із потреб обчислення площі плоских фігур, об’єму тощо. Суть методу полягає в тому, що, наприклад, для обчислення площі плоских фігур їх розкладають на нескінченну кількість нескінченно малих. Тобто, інтеграл можна розглядати як суму нескінченного числа, нескінченно малих доданків.

Будова

 Корпус - меблева плита. На корпусі нанесено систему координат та криволінійну трапецію. Вкручена система гвинтів дозволяє розбити криволінійну трапецію на прямокутники в двох варіантах. Це виконуємо за допомогою гуми риболова. Перше розбиття виконано на Рис.1.6.1. Друге розбиття – на Рис. 1.6.2. Сума площ прямокутників другого розбиття більш точно подає площу криволінійної трапеції.

Застосування

10 клас. Інтеграл – центральне поняття інтегрального числення. При вивченні цього поняття досить вдало можна застосовувати прилад «Інтеграл», оскільки він виражає основну ідею інтегрального числення. Тобто, спрощено інтеграл можна розглядати як суму нескінченного числа нескінченно малих доданків. При знаходженні площі криволінійної трапеції розіб’ємо її на прямокутники. Перше розбиття виконано на Рис.1.6.1, друге розбиття - на Рис.1.6.2. Сума площ прямокутників другого розбиття  більш точно подає площу криволінійної трапеції. Тому в подальшому розв’язуємо проблему, як найточніше знайти площу криволінійної трапеції [7].

           

РОЗДІЛ ІІ. ЗАСТОСУВАННЯ ПРИЛАДІВ НА УРОКАХ МАТЕМАТИКИ

ТА В ПОЗАКЛАСНІЙ РОБОТІ

 

2.1 Засідання математичного гуртка. «Властивість точки перетину медіан трикутника»

Означення. Центр мас системи точок залишиться попереднім, якщо точки системи замінити однією точкою, яка розміщена в їх центрі мас і якій відповідає маса, рівна сумі  мас усіх точок системи

Задача 1. Знайти центр мас двох тягарців однакової маси.

 

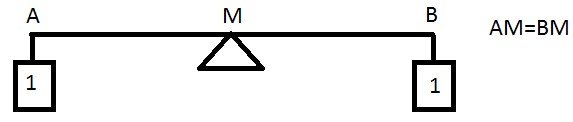
Задача 2. Знаходження центра мас важеля та двох тягарців, якщо маса одного із них в два рази більша за масу іншого. 

 

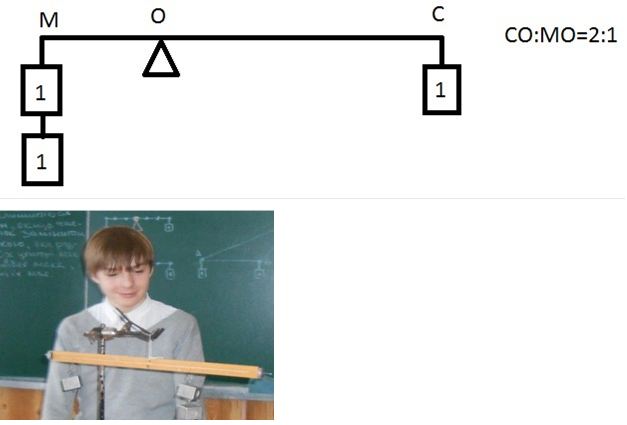
Теорема. Довести, що медіани трикутника перетинаються в одній точці  і      цією точкою діляться у відношенні 2:1, рахуючи від вершини кута.

Доведення. Нехай маємо трикутник АВС. Помістимо в точки А,В,С одиничні маси. Нехай О-центр мас цієї  системи точок.

 

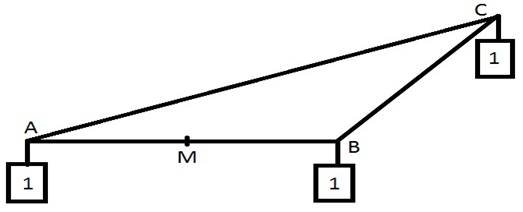
Точка М є центром мас точок А і В, СМ одна із медіан трикутника АВС.

 

 Точка О також є центром мас точки С із масою 1 та  М із масою 2, де М- центр мас точок А і В із одиничними масами. Тому точка О лежить на медіані СМ  і ділить її у відношенні СО:ОМ=2:1.Аналогічно доводимо, що інші медіани проходять через точку О і діляться нею у відношенні 2:1. 

    Обґрунтування теореми про точку  перетину медіан трикутника із застосуванням  поняття центра мас є більш близьким для учнів, причому досить чітко показано його практичне застосування. При доведенні не потрібно застосовувати велику кількість строгих математичних понять. Доступно більшій кількості учнів.   

 

 

 

2.2. Тема: Розв’язування нерівностей методом інтервалів

Мета: а) формування навиків розв'язування нерівностей методом інтервалів, зокрема, свідоме розуміння закономірностей при розв'язуванні нерівностей    вказаним           методом,     при    знаходженні         нулів,          проміжків знакосталості, причин зміни знаків при переході від одного числового інтервалу до іншого;

                б)       розвиток       пізнавального      інтересу,       формування         навичок

використовувати набуті знання та набуті вміння в нових ситуаціях;

в) формування навичок контролю та самоконтролю.

Хід уроку I. Організаційна частина.

II. Мотивація навчальної діяльності.

1). Повторення. 

Якщо  то різниця …

Якщо , то різниця …

2)  Розглянути методи розв’язування нерівностей.

а)                     б)          

 Виникає запитання як можна розв'язувати нерівності?

Скільки систем потрібно скласти?

а)     б)  і.т.д.

Тому сьогодні ми розглянемо універсальний метод розв'язування нерівностей. Використовуючи даний метод, можна розв'язувати будьяку нерівність. Хотілося б, щоб ви особливо звернули увагу на основні ідеї та специфіку методу інтервалів.

III. Розв'язування нерівностей.

1.Розв'яжемо нерівність: .

Розглянемо функцію:  

Нулі функції:  то

                                   

 

    Рис. 2.2.1

 

Рис. 2.2. 2

1). Якщо  то, (рис. 2.2.1).

 При всіх  ,  

 При всіх , то  

2). Якщо то,  (рис. 2.2.2).

При всіх , то  

При всіх , то   

Отже, для функції . Нулі     

Нулі функції розбивають числову пряму на проміжки знакосталості. На  кожному з інтервалів функція зберігає знак, причому має місце властивість чергування знаків. Знайшовши знак на крайньому зліва інтервалі, встановимо знак функції на кожному з інтервалів (рис. 2.2.3).

 

   Рис. 2.2.3

 

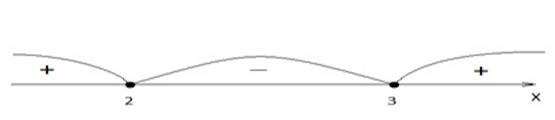
Відповідь: х

2.        Розв’язати  №284 (в)  [9]

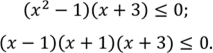
Розглянемо функцію  

Нулі функції .

 

Отже, . 

 

        Рис. 2.2.4

 

Нулі функції поділяють всю числову пряму на інтервали знакосталості, на кожному з інтервалів функція зберігає знак (рис. 2.2.4).

		3		1		1
						0
				0
		0

 

Відповідь:     

3.        Розв'язати нерівність:   

Відповідь: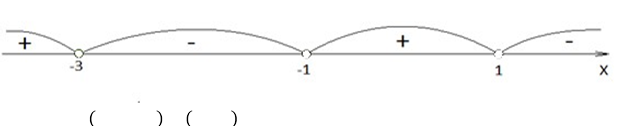                                                  

Розв'язати завдання.  №285(г), №285(в). [9]

Самостійно розв'язати. №283(а, в,є) Перевірка. [9].

. Підсумок уроку. 

Повторити алгоритм розв’язування нерівностей методом інтервалів.

 1)Знаходимо  нулі функції, яка відповідає даній нерівності.

2)  Позначаємо нулі на координатній прямій.

3)  Визначаємо знак функції, наприклад, на крайньому справа  (зліва).  4) Визначаємо знаки функції на наступних інтервалах, розставляючи їх в порядку чергування (якщо чергуються).

  5) Із усіх інтервалів вибираємо ті, які задовольняють умову.

. Домашнє завдання. 

        Ю.І.Мальований.  Опрацювати п. 5.3. Розв’язати №283 (б,г,е) №284(а,б,г).

 

2.3 Урок: «Означення синуса, косинуса, тангенса та котангенса числового аргументу»

Мета: Узагальнення і систематизація  відомих  для учнів фактів   про синус, косинус,тангенс, котангенс гострого кута та кута від 0⁰ та 180⁰. Вивчення означення синуса, косинуса, тангенса, котангенса довільного кута. Встановлення їх значень для деяких точок одиничного кола. Розвиток творчих здібностей учнів, самостійності в роботі. 

Хід уроку

Записати тему уроку. «Означення синуса,косинуса, тангенса та котангенса числового аргументу»

I. Актуалізація знань та умінь учнів

1)    Нагадати означення синуса, косинуса, тангенса та котангенса гострого кута. Значення синуса, косинуса для кутів, що дорівнюють 30⁰, 45⁰, 60⁰.

2)    Розглянемо деякі завдання на повторення.

Завдання 1. а)встановити знак абсциси та ординати кожної із позначених точок.                        б) вказати знаки проекцій радіус-векторів   та  на осі координат. Зробити висновок про координати точок кола та про проекції відповідного радіус-вектора.

 

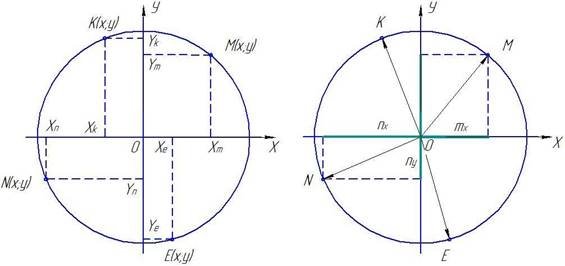
         Рис. 2.3.1, завдання 1(а).                Рис. 2.3.2 завдання 1(б). а)Відповідь:                                                    а)Відповідь:

Завдання 2. Знайдіть радіанну міру кута, який дорівнює:

1)     180⁰=рад   то  360⁰=            ;     540⁰=        ;    720⁰=          .

2)     90⁰=                    270⁰=            .    

3)     30⁰=                   150⁰=               ;    210⁰=           ;   240⁰ =         .

.4) 60⁰=                    120⁰=            ;  240=            .   

 Завдання 3. Записати числа в порядку спадання:

а) 0,5;  0;  0,01;  0,88;  1.                  Відповідь.

б) -0,5; 0; -0,01; -0,88; -1.               Відповідь.

Завдання 4. Вказати координати точок, враховуючи радіуси відповідного кола.                       а)    R=5                                                    б)    R=1

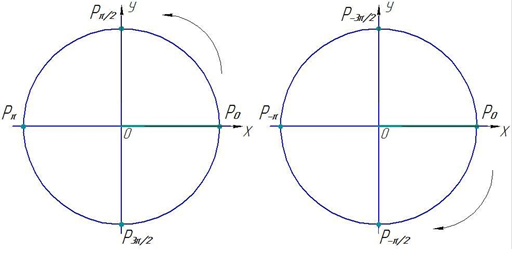
Відповідь: Р₀(    ;    )      Р_п/2(     ;    )                 Відповідь:Р₀(     ;    )   Р_-п/2(    ;    )

                   Р_п(     ;    )        Р_3п/2(    ;    )                             Р_-п(     ;    )   Р_-3п/2(     ;    )

Зауваження. Нагадати ,що кожна точка координатної площини має дві координати.

II. Вивчення нового матеріалу  (рис. 1.1.1).

Нагадати учням тему та дидактичну мету уроку.

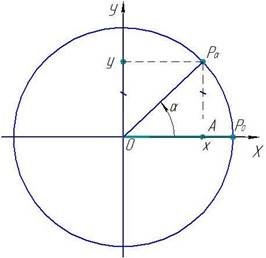Повторити  означення синуса, косинуса, тангенса та котангенса гострого кута.

Звернемося до одиничного кола. Тобто, нехай  R=1   і  Р₀(1;0), (x;y).

- прямокутний (А=90⁰).

  ;      tg;   ctg.

Якщо R=1 то   ;         ;   ctg.

Означення.  Синусом  кута повороту  називають ординату y  точки Р(х;у)  одиничного кола, яку отримано з  точки  Р₀(1;0) у результаті повороту навколо

початку координат на кут  

Означення.  Косинусом  кута повороту  називають абсцису  х точки Р(х;у)                 одиночного кола, яку отримано з  точки  Р₀(1;0) у результаті повороту навколо

початку координат на кут  

 Означення. Тангенсом кута повороту називають відношення синуса цього

кута до косинуса (

Означення. Котангенсом кута повороту   називають відношення косинуса

цього кута до синуса  

Розглянути означення синуса та косинуса за допомогою  моделі тригонометричного кола.    (Рис. 1.1.1, Рис.1.1.4 – Рис. 1.1.7) 1) Означення.

2)    Значення синуса, косинуса, тангенса та котангенса в особливих точках.

3)    Найбільше та найменше значення синуса й косинуса.

4)    Залежність синуса та косинуса від кута повороту.

 

III. Розв’язування вправ.

Завдання 5.(ЗНО 2011р). На координатному колі зображено точку 

Р(-0,8;0,6) і кут α. Визначити cosα.

 

 

А	Б	В	Г	Д
-0,8	-0,6	0,6	0,8	-√3/4

А	Б	В	Г	Д
0,5	-√3/2	-0,5	√3/2	-√3

Завдання 6. (Домашнє завдання). На одиничному колі зображено точку  Р(-0,5; -√3/2) і кут α. Визначити sinα.

 

 

 

 

 

Завдання 7. (Рис. 1.1.1)

Записати кординати відновідної точки  та  значення синуса, косинуса, тангенса та котангенса для вказаних кутів, якщо R=1.

         

                   

	α=0	α= /2	α=	α=3 /2	α=2
( x; y)	Р0(    ;    )	Рп/2(    ;    )	Рп(   ;   )	Р3п/2(    ;   )	Р2п(    ;    )
sin α
cos α
tg α
ctg α

Завдання 8.( Рис.1,1,1),  Записати кординати відновідної точки  та  значення синуса, косинуса, тангенса та котангенса для вказаних кутів, якщо R=1.

	α=0	α=- /2	α=-	α=-3  /2	α=-2
( x; y)	Р0(    ;    )	Р-п/2(    ;    )	Р-п(   ;   )	Р-3п/2(   ;  )	Р-2п(    ;    )
sin α
cos α
tg α
ctg α

IV. Підсумки уроку Повторення означення тригонометричних функцій.

Звернути увагу, що кожному куту поворту  відповідає  єдина точка одиничного кола. Отже, кожному значенню кута   відповідає єдине значення синуса, косинуса, тангенса , котангенса. Тому маємо функціональну залежність, тобто функцію. Яке найбільше та найменше значення приймає синус(косинус)?

Розглянути питання про їх зростання та спадання.  V. Домашнє завдання. 

Повторити означення синуса, косинуса, тангенса, котангенса гострого кута.

Вивчити: 

1)Означення. Синусом  кута повороту  називають ординату y  точки Р(х;у) одиничного кола, яку отримано з  точки  Р₀(1;0) у результаті повороту навколо початку координат на кут  

Означення. Косинусом кута повороту  називають абсцису х точки Р(х;у) одиничного кола, яку отримано з точки Р₀(1;0) у результаті

повороту навколо початку координат на кут  

Означення.Тангенсом кута повороту називають відношення синуса

кута до косинуса.   (

Означення. Котангенсом кута повороту   називають відношення косинуса цього кута до синуса.     (  

Заповнити таблицю.

0

Виконати завдання № 6, №8. А. Г. Мерзляк  № 513. 

 

2.4.  Урок «Площа трикутника»

Мета: а) засвоювати  учнями зміст та ідеї доведення теорем про площу трикутника і наслідків з них.

          б)  розвивати логічне мислення,  конструкторські нахили, пам’ять.

          в)  виховувати вміння і навички міркувань, самостійність, інтерес до                    предмета, впевненість у собі.

Сформувати вміння:

            ідтворювати зміст вивчених формул;              записувати формули відповідно до заданих позначень трикутників;              використовувати формули до розв'язування задач.

Прилади та матеріали: Динамічні моделі паралелограма, прямокутника та прямокутного,гострокутного, тупокутного трикутників. Хід уроку І. Організаційна частина.

ІІ. Перевірка виконання домашнього завдання

Математичний диктант

1. Знайти площу прямокутника, сторони якого  а=3 м, в=5м.

 

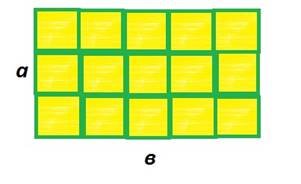
). Знайдіть площу прямокутника 𝘈𝘉𝘊𝘋, якщо 𝘈𝘉 = 9см, 𝘉𝘊 =  4 см. 

3). Знайдіть площу квадрата зі стороною а=5 см.   

 

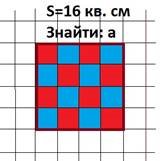
4). Знайдіть сторону квадрата, якщо його площа дорівнює  а) 16 см².    б) 10 см². 

 

 

5.                 Знайдіть площу паралелограма, якщо сторона паралелограма й проведена до неї висота відповідно дорівнюють 16 см і 9 см.

6.                 Сторони паралелограма дорівнюють 10 см і 15см. Висота, проведена до більшої сторони, 20 см. Знайти іншу сторону паралелограма. III. Актуалізація знань та умінь учнів

}      1)  Що називається висотою трикутника ? 

}      2) Скільки висот можна провести в одному трикутнику ? 

}      3) Чи існує трикутник, у якого : 

}      а) дві висоти рівні ; 

}      б) три висоти рівні ? 

}      4) Чи існує трикутник, висота якого збігається зі стороною ? 

}      5) Практична робота. За допомогою кульки з використанням сили тяжіння побудувати висоти: 

             а)  в гострокутному трикутнику (тягарець, трикутник)

             б) в тупокутному трикутнику ( Рис.1.3.1, Рис. 1.3.2)

 

IV. Вивчення нового матеріалу

Площа трикутника (Рис. 1.3.5, Рис.1.3.6).

Геометричне встановлення формули та обґрунтування формули  знаходження площі трикутника.

Теорема. Площа трикутника дорівнює половині добутку сторони на    висоту,  опущену  на цю сторону.

S_.  

 

Площа прямокутного трикутника  (Рис. 1.3.7, Рис. 1.3.8).

 

Теорема. Площа прямокутного трикутника дорівнює половині добутку його катетів.

S де а,b- катети прямокутного трикутника. 

Теорема. Площа прямокутного трикутника дорівнює половині добутку гіпотенузи на висоту, проведену до  гіпотенузи.

S, де с-гіпотенуза, h- висота прямокутного трикутника, проведена до  гіпотенузи

Властивості площі трикутника

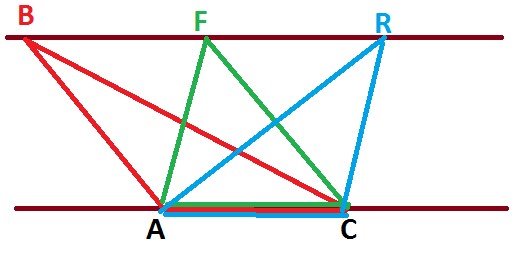
1. Враховуючи, що в трикутнику можна провести три висоти, маємо:

 

 

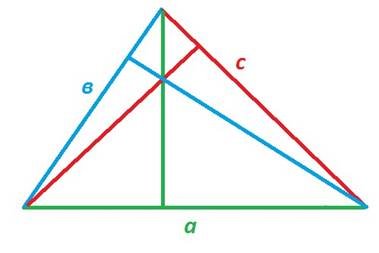
S=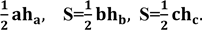

Тоді               

Використовують ,  наприклад,       і т.д.

-         Висоти трикутників обернено пропорційні довжинам сторін, до яких їх проведено.

 

 

 

2. 

 

-         Якщо трикутники мають рівні основи, а їхні вершини лежать  на прямій, яка паралельна основі, то вони мають рівні площі  (Рис. 1.3.9).

Розв’язування задач

1) Знайти площу трикутників

 

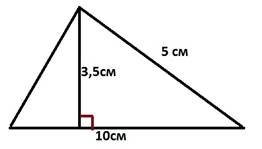
а)  

                                                                           б)

 

             

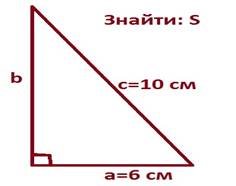
в)                                                             г)

2)  У трикутнику АВС: АС=12 см, а висота, проведена до неї, дорівнює 10 см.

Знайти висоту, проведену до сторони ВС, якщо ВС=5 см.

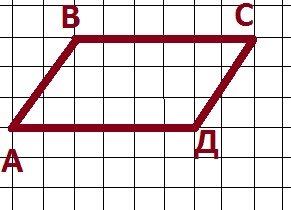
3)  У трикутнику АВС: ВС=18 см, а висота проведена до цієї сторони, -10 см. Знайти сторону АВ, якщо висота , проведена до сторони АВ, дорівнює 12 см. 4) На папері у клітинку зображено паралелограм АВСД,вершини якого збігаються з вершинами клітинок (див. рисунок). Знайдіть площу

паралелограма АВСД, якщо кожна клітинка є квадратом зі стороною завдовжки 1 см.

 

А	Б	В	Г	Д
2 9 см	2 12 см	2 12 см	2 18 см	24 м2

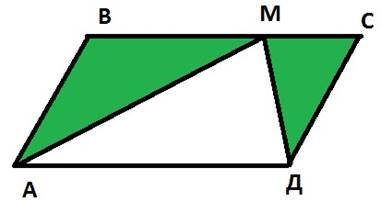
5) На рисунку зображено паралелограм АВСД, площа якого дорівнює 60 см². Точка М належить стороні ВС. Визначте площу фігури, що складається з двох зафарбованих трикутників.

 

А	Б	В	Г	Д
2 20 см	2 30 см	2 35 см	2 40 см	2 45 см

 

V. Підсумок уроку

а) площа паралелограма дорівнює  S=a, то площа трикутника …

б) площа прямокутника дорівнює S=a, то площа прямокутного трикутника … 

в) площа трикутника дорівнює S, то площа прямокутного трикутника … 

VI. Домашнє завдання

Розв’язати задачі №3, №4, №5.Г. В. Апостолова.  Опрацювати п.8, п.13. [8] ВИСНОВОК

 

Використання наочного обладнання на уроках та в позаурочний час дозволяє більш доступно та глибоко засвоїти учнями математичні поняття, краще усвідомити їх місце та значення в практичній діяльності. Підвищується інтерес учнів до уроків математики, руйнуються психологічні бар’єри, які виникають у зв’язку з труднощами при вивченні нового матеріалу.

Застосування наочності допомагає учням без зайвого напруження сприймати навчальний матеріал, надає їм впевненості у своєму розумінні математики, підвищує їх самооцінку. При цьому активізація пізнавальної діяльності дозволяє справлятися зі значним обсягом навчального матеріалу (вивчення  площі фігур).

Використання проблемного  навчання дозволяє організувати урок так, що на основі аналізу фактів, розглянутих за допомогою наочного приладдя, учні самостійно роблять висновки й узагальнення, формулюють разом із учителем певні поняття, закони, постійно перебувають в стані творчого пошуку. Цікавість  учнів до уроку підвищується тим, що вони відчувають здивування при зіставленні нового з раніше відомим (вивчення поняття інтегралу).

Опорні схеми й таблиці використовуються як елементи випереджувального  навчання. На уроці створюються ситуації переходу від виконання простих завдань, доступних кожному учневі, до складніших, які вимагають творчого застосування знань (вивчення поняття похідної). 

Наочне обладнання на уроці дозволяє учням стати учасниками наукового  та творчого пошуку, зробити перші кроки у дослідницькій діяльності.

 

СПИСОК ВИКОРИСТАНОЇ ДЖЕРЕЛ

 

1.     Державний стандарт базової і повної середньої освіти, №1392 від 23 листопада 2011р.

2.     Конфорович А.Г. Реальність і логіка математичних моделей // У світі математики. - Випуск 12. - К.: Рад. шк., 1981. - С. 58-7

3.     Стерневська Т. Математичне моделювання // Математика - 2006, №11 - С. 7-

11.

4.     Слєпкань З.І. Методика навчання математики. - К.: Зодіак ЕКО, 2000. - С. 120-124.

5.     Соколенко Л.О., Філон Л.Г., Швець В.О. Прикладні задачі природничого характеру в курсі алгебри і початків аналізу:практикум. Навчальний посібник. – Київ:НПУ імені М.П.Драгоманова, 2010. – 128с.

6.     Апостолова Г. В. Геометрія : 8 : дворівн. підруч. для загальноосвіт. навч. закл./ Г. В. Апостолова.- К. : Генеза, 2008. – 272с. 

7.     Нелін Є. П. Алгебра. 11 клас : підруч. для загальноосв. навч. закладів : академ. рівень, проф. рівень / Є. П. Нелін, О.Є. Долгова. – Х. : Гімназія, 2011. – 448 с. : іл.

8.     Мерзляк А.Г. Алгебра і початки аналізу : підруч. для 10 кл. загальноосвіт. навч. закладів : академ / А. Г. Мерзляк, Д.А. Номіровський, В.Б.

Полонський, М.С. Якір. – Х. : Гімназія, 2010 – 352с. : іл. 

9.     Мальований Ю. І., Литвиненко Г. М., Возняк Г. М. Алгебра: Підручникдля 9 класу загальноосвітніх навчальних закладів/За ред. Ю. І. Мальваного.            

–Тернопіль: Навчальна книгаБогдан, 2009. 288 с.