МОДЕЛЮВАННЯ ЗІРЧАСТИХ МНОГОГРАННИКІВ

ЗМІСТ

 

ВСТУП	4
РОЗДІЛ 1. ПОНЯТТЯ БАГАТОГРАННИКА	6
1.1. Дещо з історії	6
1.2. Правильні багатогранники	7
РОЗДІЛ 2. МОДЕЛЮВАННЯ ЗІРЧАСТИХ БАГАТОГРАННИКІВ	11
2.1. Зірчасті багатокутники	11
2.2. Моделі зірчастихбагатогранників 2.3. Тіла Кеплера-Пуансо та їх моделювання	12 15
РОЗДІЛ 3. ЗАСТОСУВАННЯ БАГАТОГРАННИКІВ	19
ВИСНОВКИ	21
Список використовуваних джерел	22
ДОДАТКИ	23

ВСТУП

 

 

"Математика володіє не лише істиною, але і вищою красою - красою вигостреної і строгої, піднесено чистої прагнучої до  справжньої досконалості, яка властива лише найбільшим зразкам мистецтва"

Бертран Рассел.

Математика - це не лише струнка система законів, теорем, завдань, але і унікальний засіб пізнання краси. Вона виражає вищу доцільність устрою світу, підтверджує універсальність математичних закономірностей, які діють однаково ефективно в кристалах і в живих організмах, в атомах і у Всесвіті, у витворах мистецтва і наукових відкриттях.     Краса допомагає з радістю сприймати навколишній світ, математика дає можливість усвідомити явища і зміцнити знання про гармонію всього світу.             

Вивчаючи математику, ми відкриваємо усе нові і нові складові краси, наближаючись до розуміння, а потім і до створення краси і гармонії.        

Робота, пропонована вашій увазі, присвячена захоплюючому розділу геометрії - теорії багатогранників, а, якщо говорити конкретніше - зірчастим багатогранникам.

Актуальність моєї роботи полягає в тому, що вчені в наші дні вивчають багатогранники і складають різні наукові гіпотези, які в майбутньому можуть привести до різних відкриттів. Ця тема актуальна, оскільки небагато людей знають правильні багатогранники, але знання цих геометричних тіл допоможе в створенні різних шедеврів (як у архітектурі, так і в живописі і багато в чому другому, тому що багатогранники мають велику сферу застосування).                           

Метою моєї роботи є розкриття таємниці моделювання зірчастих багатогранників. При написанні цієї роботи були поставлені наступні завдання:              

1.     Простежити історію розвитку багатогранників.
2.     Розширити знання про зірчасті багатогранники.
3.     Досліджувати способи виготовлення різних моделей зірчастих багатогранників.
4.     Довести, що багатогранники - складові прекрасного.

Об’єктом дослідження став зірчастий многогранник, який моделювався за допомогою різних способів.

Методи дослідження: збір фактів, зіставлення, аналіз і синтез; абстрагування, спостереження, порівняння; експериментальний метод – моделювання; вимірювання.

Чим привабливі многогранники? Вони мають багату історію, яка пов'язана з такими знаменитими ученими старовини, як Платон,   Евклід, Архімед, Кеплер.

   

   Платон             Архімед          Евклід          Кеплер

Тут не лише відкривається дивний світ геометричних тіл, що мають неповторні властивості, але і цікаві наукові гіпотези. Жодні геометричні тіла не мають такої досконалості і краси, як правильні многогранники. Людина виявляє цікавість до правильних багатокутників і многогранників упродовж усієї своєї свідомої діяльності - від дворічної дитини, що грає дерев'яними кубиками, до зрілого математика. Деякі з правильних і напівправильних тіл зустрічаються в природі у вигляді кристалів, інші - у вигляді вірусів, які можна розглянути за допомогою електронного мікроскопа.

Найбільше мене зацікавили  "Зірчасті багатогранники" - спорідненість істини і краси. Складні "кирпаті" моделі, складність у виготовленні, декоративність - саме це притягнуло мене в них і підштовхнуло на виконання дослідницької роботи спільно з моїм педагогом.

 

РОЗДІЛ І

ПОНЯТТЯ БАГАТОГРАННИКА

 

 

1.            Дещо з історії

 

"Теорія багатогранників, зокрема опуклих багатогранників, - одна з самих захоплюючих глав геометрії", - така думку Л.А. Люстерника, члена-кореспондента Академії наук СРСР, ученого, що багато зробив саме в цій області математики.

Поняття багатогранника є одним з центральних в курсі стереометрії. Багатогранники виділяються своїми цікавими властивостями, красивими формами. Теорія багатогранників має багату і древню історію, пов'язану з іменами Піфагора, Евкліда, Архімеда, Аполлонія. В той же час це сучасний розділ математики. Глибокі результати в ній отримані радянськими математиками Б.Н. Делоне, А.Д. Александровим, А.В. Погореловим. Теорія багатогранників має велике значення як для теоретичних досліджень по геометрії, так і для практичних застосувань в інших розділах математики, наприклад алгебрі, теорії чисел, в природознавстві.

Багатогранниками зазвичай називаються тіла, поверхні яких складаються з кінцевого числа багатокутників, званими гранями багатогранника. Сторони і вершини цих багатокутників називаються відповідно ребрами і вершинами багатогранника. Діагоналлю багатогранника називається відрізок прямої, що сполучає дві вершини, що не лежать в одній грані. Діагональною площиною багатогранника називається площина, що проходить через три вершини багатогранника, що не лежать в одній грані.

Поняття опуклості - одне з найважливіших понять математики. Воно з'явилося відносно нещодавно. Основи теорії опуклих багатогранників були закладені у кінці XIX ст. німецькими ученими Г. Брунном, Г. Мінковським і розвинені в XX столітті радянськими ученими Б.Н. Делоне, А.Д. Александровим, А.В. Погореловим.

Багатогранник називається опуклим, якщо він є опуклою фігурою, тобто разом з будь-якими двома своїми точками містить і відрізок, що сполучає їх. Опуклий багатогранник називають правильним, якщо усі його грані є правильними багатокутниками з одним і тим же числом сторін і в кожній вершині багатогранника сходиться одне і те ж число ребер.

 

1.2 Правильні багатогранники

 

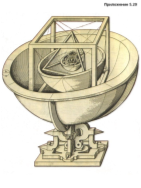
Рис.1.1. "Космічний кубок"

 

Ще за часів древніх греків був встановлений вражаючий факт - існує всього п'ять правильних опуклих багатогранників різної форми. Уперше досліджені піфагорійцями, ці п'ять правильних багатокутників були згодом детально описані Платоном і стали називатися в математиці платоновими тілами.

И. Кеплер побудував на основі правильних багатогранників модель Сонячної системи. Така модель Сонячної системи дістала назву "Космічного кубку" Кеплера Рис.1.1.

Існування тільки п'яти правильних багатогранників представлялося вченим фундаментальним фактом, який повинен мати пряме відношення до будови матерії у Всесвіті. Піфагорійці вважали багатогранники божественними. Згідно з їх переконаннями, атоми основних елементів повинні мати форму різних платонових тіл: атоми вогню - форму тетраедра, землі - форму куба, повітря - форму октаедра, води - форму ікосаедра. Старогрецький вчений Платон зв'язав з цими тілами форми атомів основних стихій природи. (Стихіями натурфілософії називали речовини, з яких, шляхом згущування і розрідження, охолодження і нагрівання утворюються усі тіла.) Піфагорійці вважали, що вогонь складається з найдрібніших (а тому невидимих) часток, що мають форму тетраедра. Їх переконання грунтувалися на тому, що, оскільки серед опуклих правильних тіл тетраедр має найменше число граней і найбільш "гострі" багатогранні кути при вершинах, то він має найбільшу проникаючу здатність. Правильний тетраедр є простим з п'яти Платонових тіл, він має раціональну конструкцію: високу міцність при малій вазі. Найбільш нерухомою із стихій – землі піфагорійці ставили у відповідність найстійкіший багатогранник - куб.

За допомогою простих і складних атомів Платон спробував навіть відбити взаємини між стихіями: 1 вода = 2 повітря + 1 вогонь Рис. 1.2.

Це "рівняння" потрібно розуміти так: в елементі води - ікосаедрі - 20 граней, утворених рівносторонніми трикутниками, які складені шістьма прямокутними трикутниками. Платон представляв атоми як плоскі тіла - прямокутні трикутники двох видів: одні рівнобедрені, інші з катетом, рівним половині гіпотенузи.

 

/ вогонь	/ тетраедр
/ вода	/ ікосаедр
/ повітря	/ октаедр
/ земля	/ гексаедр
/ всесвіт	/ додекаедр

Рис. 1.2.

П'ять правильних тіл вивчали Театет, Платон, Евклід, Гипсикл, Папп. Також надзвичайно високий був інтерес до правильних багатогранників в кругах художників, скульпторів, архітекторів. Ними займалися Леонардо да Вінчі, Альберт Дюрер.

Отже, існує всього п'ять правильних багатогранників.

Простим серед багатогранників є тетраедр (чотиригранник - від грецького "тетра", тобто чотири). Його чотири грані - рівносторонні трикутники. Чотири - це найменше число граней, що відділяють частину тривимірного простору. Проте, тетраедр має багато властивостей, характерних для однорідних багатогранників. Усі його грані суть правильні багатокутники, причому кожна відділяється ребром в точності від однієї грані. Усі багатогранні кути тетраедра також рівні між собою.

Куб, або гексаедр (шестигранник - від грецького "гекса", тобто шість) - самий загальновідомий і широко використовуваний багатогранник. Усі шість його граней - квадрати, що сходяться по два уздовж кожного ребра і по три в кожній вершині.

Октаедр (восьмигранник - від грецького "окта", тобто вісім), складений з восьми правильних трикутників, його протилежні грані лежать в паралельних площинах. Йоганн Кеплер (1571-1630) у своєму етюді "Про сніжинку" висловив таке зауваження: "Серед правильних тіл найперше, початок і батько інших - куб, а його, якщо дозволено так би мовити, дружина - октаедр, бо у октаедра стільки кутів, скільки у куба граней".

Ікосаедр (двадцятигранник - від грецького "ікос", тобто двадцять), складений з двадцяти правильних трикутників. Ікосаедр - одне з п'яти тіл, по простоті що йде за тетраедром і октаедром. Їх об'єднує та обставина, що гранями кожного являються рівносторонні трикутники.

І загадковий додекаедр (дванадцятигранник - від грецького "додека", тобто дванадцять), складений з дванадцяти правильних п'ятикутників. У відомому сенсі додекаедр представляє найбільшу привабливість серед тіл, змагаючисьсь з ікосаедром, який майже йому не поступається (а можливо, в чомусь і перевершує).

 

 

 

 

РОЗДІЛ ІІ

МОДЕЛЮВАННЯ ЗІРЧАСТИХ БАГАТОГРАННИКІВ

 

 

2.1. Зірчасті багатокутники

 

Термін «зірчастий» має спільний корінь зі словом «зірка», і це вказує на його походження. Існують зірчасті багатокутники і зірчасті багатогранники. Щоб розібратися в суті справи, звернемося до креслень і моделей.

Почнемо з найпростішого багатокутника - рівностороннього трикутника. Подивимося, що станеться, якщо ми продовжимо всі три його сторони. Легко помітити, що цими прямими не буде обмежена ніяка нова частина площини: продовження сторін будуть розходитися. Аналогічна картина постане перед нами і в тому випадку, якщо ми спробуємо продовжити боки квадрата. Побудовані прямі будуть попарно паралельні і не перетнуться, скільки б їх не продовжували. Тим самим вони не додадуть ніяких нових обмежених частин площині в середині квадрата. Однак в разі п'ятикутника картина змінюється. Продовження сторін п'ятикутника перетинаються у зовнішній по відношенню до п'ятикутника частині площини, додаючи до п'ятикутника нові частини. В результаті виходить добре відома нам п'ятикутна зірка, яку називають пентаграма. Пентаграма була відома в глибокій старовині, що випливає хоча б з того, що піфагорійці вважали її символом здоров'я. Продовження сторін шестикутника призводить до появи шестикутної зірки, або гексаграми (останню можна розглядати не як єдиний багатокутник, а як з'єднання двох рівносторонніх трикутників).

Аналогічно правильний восьмикутник (Октагон) приводить нас до восьмикутної зірки - октаграмма, правильний десятикутник (декагон) - до десятикутної зірки, або декаграмма. Рис. 2.1  Пентаграмму, октаграмму і декаграмму можна розглядати як нероздільні єдині багатокутники відповідно з 5, 8 і 10 сторонами, оскільки існує безперервний обхід їх вершин на всі боки навколо центрів. При цьому в разі пентаграми, наприклад, здійснюючи повний обхід в порядку, визначеному номерами 0-5, ми робимо два оберти навколо центру пентаграми, тоді як під час обходу п'ятикутника ми робимо лише один оберт. У разі ж октаграми і декаграми виходить по три оберти навколо центру. Зауважимо, що внутрішні точки перетину ми не розглядаємо як вершини зірки. Вказана вище обставина враховується в символічних позначеннях зірчастих многокутників. У нашому випадку пентаграма, октаграма і декаграма позначаються відповідно через 5/2, 8/3 і 10/3. Ці зірки можуть приймати, крім того, і інші обриси, але в подальшому ми будемо говорити лише про описані вище форми.

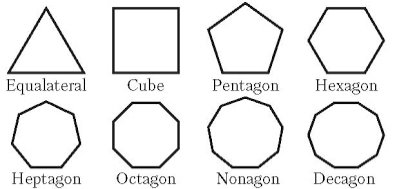
Рис. 2.1

 

2.2. Моделі зірчастих багатогранників

 

Якщо тепер звернутися до аналогічного процесу в тривимірному просторі, то природно знову почати з найпростішого багатогранника - тетраедра. Зрозуміло, тут нам потрібно продовжити не ребра, а грані багатогранника. Однак чотири площини - продовження граней тетраедра - обмежують лише ту частину тривимірного простору, яка збігається з вихідним тілом. Шість площин куба попарно паралельні і взаємно перпендикулярні, подібно сторонам двовимірного аналога куба - квадрата. Тому і в тривимірному випадку до кубу не додається жодних нових частин. Але вже випадок октаедра дає цікаві результати. Вісім площин - продовження граней октаедра - відокремлюють від простору нові частини, так би мовити, «відсіки», зовнішні по відношенню до октаедра. Ви виявите, що ці частини є ні чим іншим, як малі тетраєдри, грані яких збігаються з гранями октаедра. Якщо ви тепер подумки приєднаєте ці частини до октаедру таким чином, щоб їх спільні з октаедром грані зникли, залишивши середину нового тіла порожнистим, перед вашим поглядом виникне неопуклий багатогранник.

Однак з таким же успіхом ви можете уявити собі цей багатогранник і у вигляді безлічі пересічних трикутних граней, вершини яких співпадають з вершинами малих тетраедрів. Ці трикутні грані мають властивість, зазначеним у опуклих багатогранників, а саме: кожне ребро цих трикутників належить в точності двом таким граням. Зрозуміло, ці ребра перетинаються, але внутрішні точки перетину цих відрізків не слід розглядати в якості вершин багатогранника, подібно до того як ми поступали в разі плоских зірчастих багатогранників. Адже і там кожна сторона, наприклад пентаграма, перетиналася двома іншими, але точки їх перетину не розглядаються як ті, що ділять сторону. Подібним же чином в зірчастому октаедрі ми знаходимо лише вісім граней, і тільки кінці ребер вважаємо вершинами багатогранника.

Втім, подальше ретельне вивчення наводить нас на думку про те, що цей багатогранник насправді є не єдине тіло, але з'єднання двох пересічних тетраедрів, центри яких співпадають з центром вихідного октаедра, причому ця точка є центром симетрії всього тіла. Цей багатогранник відкрив Кеплер в 1619 році і дав йому ім'я stella octangula1. Рис.2.2

Ще одна особливість цього тіла полягає в тому, що вісім його вершин лежать в вершинах деякого куба, а ребра є діагоналями граней цього куба.

Продовжувати далі грані октаедру не має сенсу, бо вони не відокремлять більш ніякої частини простору, не створять нових «відсіків». Тому октаедр має лише о д н у зірчасту форму.

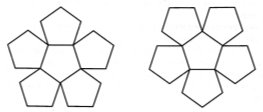
Якщо ж звернутися до додекаедрів, продовживши його межі як і в разі октаедра, можна виявити, що це призведе до утворення трьох різних типів відсіків. Поблизу самого додекаедру є 12 п'ятикутних пірамід. Ці піраміди перетворюють додекаедр в малий зірчастий додекаедр. За ними слідують 30 клиноподібних відсіків, що перетворюють малий зірчастий додекаедр в великий додекаедр. Нарешті 20 трикутних біпірамід2 перетворюють великий додекаедр в великий зірчастий додекаедр, який, мабуть, точніше було б назвати зірчастим великим додекаедром. Це завершальна Зірчаста форма Додекаедра, який має три такі форми: дві з них були відкриті Кеплером (1619), третя - Пуансо (1809).

Рис. 2.3

Тепер вас, можливо, зацікавить ту обставину, що на відміну від октаедра кожна з зірчастих форм додекаедру не є з'єднанням Платонових тіл, але утворює новий багатогранник. Насправді ці багатогранники правильні, оскільки два з них мають гранями по 12 пересічних пентаграм, а межі третього - 12 пересічних п'ятикутників (Пентагону).  Коші (1811) довів, що ці три багатогранника, відкриті раніше, насправді не що інше, як зірчасті форми додекаедра. Він також встановив, що разом з великим ікосаедра - зірчастої формою ікосаедра - вони є єдино можливими правильними зірчастими тілами. Так, до п'яти правильним тіл, відомим ще древнім вченим, математики ближчою до нас епохи додали чотири зірчастих багатогранника, гранями яких можуть бути правильні або зірчасті багатокутники. Як і раніше грані з'єднуються попарно в ребрах, але до цього вони перетинаються з іншими гранями. При цьому внутрішні лінії перетину не зважають ребрами. Всі ці властивості чітко простежуються на моделях зірчастих тіл.

Перед побудовою цих моделей цікаво ознайомитися з пристроєм трафаретів, які задають якусь одну лицьову зірчасті грань. Решта межі мають аналогічну будову. Трафаретом для октаедра служитиме рівносторонній трикутник, з якого слід вирізати трикутник з вершинами в серединах сторін. Цей внутрішній трикутник є межею вихідного октаедра, поза яким розташована stella octangula. Трафаретом для додекаедру служить зірчастий багатокутник без вирізаного зірчастого багатокутника. Нумерація показує, які частини утворюють зовнішні по відношенню до граней шматки. За допомогою таких трафаретів можна зробити заготовки, необхідні для виготовлення моделей.

 

2.3 Тіла Кеплера_Пуансо та їх моделювання

 

Зірчастий Додекаедр. Великий зірчастий додекаедр належить до сімейства тіл Кеплера-Пуансо, тобто правильних неопуклих багатогранників. Грані великого зірчастого Додекаедра - пентаграми, як і у малого зірчастого додекаедра, у кожної вершини з'єднуються три грані. Вершини великого зірчастого Додекаедра збігаються з вершинами описаного додекаедру.

Великий зірчастий додекаедр був вперше описаний Кеплером в 1619г. Це остання Зірчаста форма правильного додекаедра.

Моделювання малого і великого зірчастого додекаедра (Додаток 1)

Для виготовлення моделі багатогранника з щільного паперу, картону або іншого матеріалу досить виготовити його розгортку і потім склеїти відповідні ребра. Для зручності склеювання розгортку багатогранника виготовляють з клапанами, по яких і виробляється склеювання.

Модель малого зірчастого додекаедра дуже просто виготовити з моделі правильного додекаедра. Досить виготовити 12 правильних п'ятикутних пірамід з ребрами основ, рівними ребру правильного додекаедра, і наклеїти їх на усі грані правильного додекаедра.

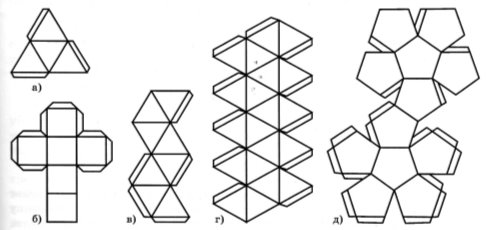
Рис. 2.2.

Таким чином, спочатку треба виготовити модель правильного додекаедра. Її можна склеїти з розгортки. Рис. 2.2. д) Після того, як модель правильного додекаедра готова, будується модель відповідної правильної піраміди, розгортка якої показана на малюнку.

Необхідно виготовити 12 таких пірамід по числу граней правильного додекаедра і наклеїти їх на його грані. Модель малого зірчастого багатогранника готова.

Виготовлення різних моделей багатогранників з розгорток описав англійський математик М. Веннинджер в книзі "Моделі багатогранників". Наведемо декілька прикладів.

Великий ікосаедр. З описаних досі багатогранників, мабуть, найкрасивішим і декоративним є великий ікосаедр - останній з чотирьох правильних зірчастих багатогранників Кеплера - Пуансо. Його вершини представляють собою центри правильних п'ятикутних зірок, які виступають з тіла багатогранника. Це властивість ріднить великий ікосаедр з великим додекаедром і виділяє ці два тіла з усієї безлічі однорідних багатогранників. Багато однорідних багатогранників мають зірчасті грані, але подібної будови вершин ви більше не зустрінете.

Зробити модель великого ікосаедра неважко. Заготівля для неї дуже проста, і, якщо слідувати запропонованому методу побудови, модель виявиться дуже міцною і жорсткою, хоча і пустою усередині. П'ятикольорове розфарбування займе більше часу, але на це варто піти. Справа приведена парна таблиця розмальовки, відповідно до якої склеюються показані на малюнку частини моделі. (Додаток 2)

Кожна частина складається з п'яти пар заготовок, з'єднаних в своєрідне віяло. Його слід перегнути на манер гармошки так, щоб вниз опустилися внутрішні ребра кожної пари, а сусідні ребра різних пар піднялися. Склеївши вільні ребра, ви отримаєте вершину частини моделі. Після цього малі трикутник підклеюються на свої місця, так що утворюється п'ятикутна западина, з якої і виростає верхня частина.

Вам буде потрібно всього 12 таких частин; одна половина з них пофарбована відповідно до таблиці, а інша половина має енантіоморфну розмальовку. Ці частини з'єднуються тепер в звичайному ікосаедральном порядку, причому енантіоморфні  частини, природно, діаметрально протилежні. З'єднання сусідних частин виконуйте послідовно, склеюючи ребра один за одним. Рекомендую для цієї мети скористатися зажимами, бо двогранні кути між краями основ сусідніх частин дуже малі. Навіть останню частину варто приєднувати за допомогою затискачів. Перед склеюванням останнього ребра за допомогою пінцета видаліть затиски з сусідніх ребер, після чого капніть клей в щілину і розподіліть його по поверхні. Не засмучуйтеся, якщо в кутах п'ятикутних ребер виявляться невеликі щілини або отвори. Коли модель буде закінчена, додайте сюди пінцетом по краплині клею і трохи стисніть краю, поки клей не підсохне. Тим самим ви позбудетеся від щілин і ще більше зміцните модель. Правильно виконана модель великого икосаедра дивно красива.

Моделювання великого ікосаедра (Додаток 2)

Моделі зірчастих багатогранників дуже декоративні, проте їх виготовлення вимагає багато часу і терпіння.

Існує інший, швидший спосіб виготовлення моделей багатогранників з так званого геометричного конструктора, що складається з багатокутників, зроблених з щільного матеріалу з клапанами, що відгинаються, і гумових колечок - основної кріпильної деталі конструктора.

 

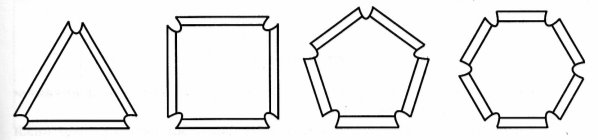
Усі багатокутники повинні мати рівні сторони. Бажано мати багатокутники декількох кольорів. Підбираючи відповідним чином багатокутники як грані багатогранника і скріплюючи їх гумовими колечками, можна отримувати моделі різних багатогранників. Для того, щоб колечка краще трималися і не заважали один одному, куточки багатокутників в конструкторі можна трохи обрізувати, як показано на малюнку.

Для того, щоб клапани добре відгиналися, потрібно по периметру багатокутника провести по лінійці, скажімо, кінцем ножиць. Оскільки потрібно буде виготовити декілька десятків граней кожного типу (найбільше трикутних, потім чотирикутних і п'ятикутних і менше всього шестикутних), то спочатку треба зробити як можна точніше шаблони граней, а потім просто обводити ці шаблони олівцем.

З такого конструктора легко збираються правильні і напівправильні багатогранники.

Можна скористатися іншим, дуже цікавим і незвичайним способом виготовлення правильного додекаедра, який полягає в наступному. Розгортку правильного додекаедра необхідно розділити на дві зірки і накласти їх одна на одну так, щоб вийшла десятикутна зірка. Цю зірку слід обв'язати гумкою, обходячи нею кути по черзі згори і знизу і притискуючи модель вільною рукою до столу. Опустивши руку, бачимо що зірка, що розкрилася, перетворюється на просторову модель правильного додекаедра.

РОЗДІЛ ІІІ

ЗАСТОСУВАННЯ  МНОГОГРАННИКІВ

 

 

"Правильні многогранники мають красиві форми. Вони є дивним символом симетрії, що привертав увагу видатних  мислителів. Цим і пояснюється інтерес людини до многогранників".     

Математика, зокрема геометрія, є могутній інструмент пізнання природи, створення техніки і перетворення світу. Різні геометричні форми (особливо прадавні багатогранники) знаходять своє віддзеркалення  практично в усіх галузях знань: в архітектурі, мистецтві і так далі                                       

Багатогранники в мистецтві. Леонардо да Вінчі (1452 -1519), наприклад, захоплювався теорією многогранників і часто зображував їх на своїх полотнах. Він  проілюстрував правильними і напівправильними многогранниками книгу Ченця Луки Пачоли "Про божественну пропорцію". (Додаток 3 Рис. 3.1)  Знаменитий художник, Альбрехт Дюрер (1471- 1528),  що захоплювався геометрією, у відомій гравюрі ''Меланхолія ''  на передньому плані зображував додекаедр. (Додаток 3 Рис. 3.2)

Сальвадор Далі на картині "Таємна вечеря" (1904-1989) зображував Ісуса Христа зі своїми учнями на тлі величезного прозорого додекаедра. Рис. 3.3

Голландський художник Мориц Корнилис Ешер (Додаток 3 Рис.3.4) створив унікальні і чарівні роботи, в яких використані або показані широкий круг математичних ідей.  Правильні геометричні тіла - багатогранники - мали особливу чарівність для Ешера. У його багатьох роботах багатогранники є головною фігурою і в ще більшій кількості робіт вони зустрічаються як допоміжні елементи. Витончений приклад зірчастого додекаедра можна знайти в його роботі "Порядок і хаос". Рис. 3. 5. В даному випадку зірчастий багатогранник - символ математичної краси і порядку- поміщений всередину скляної сфери. Аскетична краса цієї конструкції контрастує з безладно розкиданим по столу сміттям.                                            

Найцікавіша робота Ешера -  гравюра "Зірки", на якій можна побачити тіла, отримані об'єднанням тетраедрів, кубів і октаедрів. (Додаток 3.Рис. 3.6) Якби Ешер зображував в цій роботі лише різні варіанти багатогранників, ми ніколи б не дізналися про неї. Але він з якоїсь причини помістив всередину центральної фігури хамелеонів, щоб утруднити нам сприйняття усієї фігури.

Магнус Веннинджер (1919р.н.) батько Магнус, чернець - бенедиктинець із США. Він викладає математику у церковній школі, видає книги, бере участь у виставках і захоплюється створенням багатогранників складних форм з паперу. (Додаток 3, Рис. 3.7)                           

Правильні многогранники - найвигідніші фігури. І природа цим широко користується. Багато властивостей кристалів, які вивчаються  на уроках фізики і хімії, пояснюються їх геометричною будовою. Тому властивості багатогранників  використовуються і в кристалографії. Бджоли будували шестикутні стільники задовго до появи людини, а в історії цивілізації створення багатогранних тіл (подібних до пірамід) разом з іншими видами пластичних мистецтв йде углиб віків.                      

 Багато форм зірчастих багатогранників підказує сама природа. Сніжинки - це зірчасті багатогранники.              

Зірчасті многогранники дуже декоративні, що дозволяє широко застосовувати їх в ювелірній промисловості при виготовленні всіляких прикрас.  

Форми многогранників знаходять широке застосування в конструюванні складних і красивих багатогранних поверхонь, які використовуються в реальних архітектурних проектах. (Додаток 4, рис.3.8)

Застосовуються вони і в архітектурі. На малюнку зображена оригінальна конструкція, виконана В.Н.Гамаюновим і покладена в основу проекту адміністративної будівлі в одному з італійських міст. (Додаток 4, рис.3.9)

 Отже, багатогранники відкрили нам спроби учених наблизитися до таємниці світової гармонії і показали чарівну привабливість геометрії.

ВИСНОВКИ

 

 

Багатогранники - цікаві тіла геометрії, що мають різноманітні властивості. За зовнішньою ознакою мають відмінності, але вони об'єднані в одну групу, і об'єднує їх велика наука - геометрія. «Земні зірки» складні за своїми особливостями і властивостями, але саме складність і загадковість цих тіл і привертає різних людей вивчати їх.

 Що їх тягло? Може можливість хоч на крок наблизитися до розуміння простору, розгадки таємниці Всесвіту ... Так чи інакше, але багатогранники красуються на полотнах художників і з їх допомогою в нудну архітектуру наших міст вриваються небачені космічні форми, ними милуються, їх вивчають, конструюють, використовують.

 Математична бездоганність ліній ані трохи не обмежує творчість, фантазію людей: згадати хоча б роль цього поняття в філософських системах Давньої Греції та Риму, єгипетські піраміди, перетворення площини і простору в «неможливих» картинах М.К. Ешера.

Моделювання багатогранників сприяє розвитку просторових уявлень, конструкторських раціоналізаторських здібностей. У своїй роботі я висвітлив історію багатогранників, їх види, а також застосування. В ході дослідження розкрив таємниці моделювання багатогранників, навчився сам виготовляти різні моделі. Вважаю свою роботу цікавою, корисною і змістовною. Думаю, що всі завдання, поставлені для досягнення мети, виконані. Я отримав величезне задоволення від виконаної мною роботи, а також нову і цікаву для себе інформацію.

Моя робота може бути використана на уроках геометрії, на різних конкурсах і як ілюстративний матеріал, може допомогти розширити знання дітей по темі Багатогранники. Цією роботою хотілося б розширити Ваші уявлення про світ багатогранників і довести, що многогранники - складові прекрасного