Навчальний посібник "Математика 6 клас" 2 семестр
Посібник розроблений згідно Комбінованої системи М.П. Гузика і може бути використаний як додатковий матеріал для учнів на уроки. Він складається з п'яти тем. Кожна тема має таку структуру:
- перший урок – урок розбору блоку навчальної інформації;
- наступні уроки – уроки фронтального опрацювання матеріалу,
- між уроками фронтального опрацювання містяться завдання по підготовці до уроків індивідуального опрацювання матеріалу;
- в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен продемонструє свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.
Любий шестикласнику!
 Ти продовжуєш вивчати одну з найдавніших і найважливіших наук – математику. В оволодінні навчальним матеріалом курсу тобі допоможе цей посібник. Він складається з п’яти блоків, кожен з яких містить уроки розбору матеріалу блоку, уроки фронтального опрацювання матеріалу, уроки внутрішньопредметного узагальнення. Також посібник містить завдання по підготовці до індивідуального опрацювання матеріалу, які позначені значком .
Ти продовжуєш вивчати одну з найдавніших і найважливіших наук – математику. В оволодінні навчальним матеріалом курсу тобі допоможе цей посібник. Він складається з п’яти блоків, кожен з яких містить уроки розбору матеріалу блоку, уроки фронтального опрацювання матеріалу, уроки внутрішньопредметного узагальнення. Також посібник містить завдання по підготовці до індивідуального опрацювання матеріалу, які позначені значком .
Будь уважний, активний і наполегливий, не лінуйся і таким чином принесеш радість собі, своїм батькам і Творцю.
Нехай Бог посилає мудрості у вивченні математики!!!
Тема №6. Раціональні числа
Урок №1

Раціональні числа
«Хто з дитячих років займається математикою,
той виховує наполегливість і завзятість у досягненні мети»
О. Маркушевич, математик
Питання
- Цілі числа. Раціональні числа.
- Модуль числа.
- Порівняння раціональних чисел.
Література
Істер О.С. Математика: підручник для 6 класу, Київ: «Генеза», 2014. – §§ 33 – 37, стор. 160 – 185
|
|
1. Цілі числа. Раціональні числа |
||
|
1.1 |
Числа зі знаком «–», називають від’ємними числами. |
|
|
|
1.2 |
Числа зі знаком «+», називають додатними числами. (Знак «+» у запису додатних чисел, як правило, не пишуть). |
|
|
|
1.3 |
Число 0 не є ані додатним, ані від’ємним. |
||
|
1.4 |
Пряму з вибраними на ній початком відліку, одиничним відрізком і вказаним додатним напрямом називають координатною прямою. |
|
|
|
1.5 |
Число, якому відповідає певна точка на координатній прямій, називають координатою цієї точки. |
|
|
|
1.6 |
Числа, що відрізняються одне від одного лише знаками, називають протилежними числами. |
2 і –2; –10 і 10 |
|
|
1.7 |
Натуральні числа, протилежні їм числа і число 0 називають цілими числами |
5; –78; 25; – 56 |
|
|
1.8 |
Цілі числа та дробові числа (додатні і від’ємні) називають раціональними числами. |
1; 125; –34; – 0,25; |
|
|
|
2. Модуль числа |
||
|
2.9 |
Модулем числа називають відстань від початку відліку до точки, що зображує це число на координатній прямій.
Позначення: |
|
|
|
2.10 |
Модулем додатного числа і числа 0 є саме це число, а модулем від’ємного числа – протилежне йому число. |
|
|
|
2.11 |
Властивості модуля:
|
||
|
3. Порівняння раціональних чисел |
|||
|
3.12 |
З двох чисел меншим є те, яке на координатній прямій розміщено лівіше, а більшим – те, яке на координатній прямій розміщено правіше. |
|
|
|
3.13 |
Будь-яке від’ємне число менше за нуль і менше за будь-яке додатне число. |
|
|
|
3.14 |
З двох від’ємних чисел більшим є те, модуль якого менший, і меншим є те, модуль якого більший. |
|
|
Урок №2
«Що може бути шкідливіше за людину, котра володіє
знанням найскладніших наук, але не має доброго серця?»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Додатні і від’ємні числа. Число нуль
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
Обчисливши приклади в будиночках звіряток та скориставшись дешифратором, з'ясуй девіз уроку.






![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Дешифратор:
Дешифратор:
|
5 |
закони |
|
4,8 |
формує |
|
25 |
мовою |
|
0,75 |
математики |
|
1,5 |
природа |
|
3/4 |
свої. |
Завдання 2.
2.1. Повтори тези 1.1 – 1.3 блоку № 6.
2.2. Дай відповіді на питання:
1) Які числа називаються додатними?
2) Яким є число 0?
3) Які числа називаються від’ємними? Наведи приклад.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
 Завдання 3.
Завдання 3.

Завдання 4.
Виконай вправи, стор. 163 – 164 підручника: 849, 851, 854.
Урок №3
«Цифри не керують світом, але
вони показують, як управляється світ»
І. Гете
Фронтальне опрацювання матеріалу
Координатна пряма
І. Робота над засвоєнням понять термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.5 блоку № 6.
- Дай відповіді на питання:
- Які числа називаються додатними, а які від’ємними? Наведи по три приклади кожного виду чисел.
- Яку пряму називають координатною?
- Як на координатній прямій позначають додатний напрям?
- Яку координату має початок координат?
- Що називають координатою точки?
- Як на координатній прямій розміщені додатні і від’ємні числа?
- Які числа на координатній прямій відповідають точкам А, В, С, D?
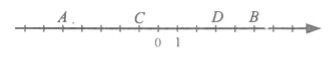
- Назвіть координати точок, в яких знаходяться певні звірята

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Виконай вправи, стор. 167 підручника: 860, 862, 864
Завдання 3.
Виконай самостійно вправу 865, стор.167 підручника.
Завдання 4.
Виконай письмово вправи, стор. 168 підручника: 870, 872, 875.
Урок №4
«Усе, що робиш, треба робити добре»
Ф.Бекон
Фронтальне опрацювання матеріалу
Протилежні числа. Цілі числа. Раціональні числа
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 1.10 блоку №6.
- Дайте відповіді на питання:
- Які числа називаються від’ємними, а які додатними?
- Які числа називаються протилежними?
- Дайте визначення координатної прямої.
- Які числа називаються цілими? Наведіть приклади.
- Які числа називаються раціональними?
- Складіть схему раціональних чисел.
- Які з перелічених ознак є суттєвими для поняття «координатна пряма»:
- На прямій позначено початок відліку.
- На прямій позначено одиничний відрізок.
- На прямій позначено напрям.
- Пряма розташована горизонтально.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
- Накресліть координатну пряму. Позначте на ній точку К (-3). Позначте на цій прямій точку, віддалену від точки К:
- у додатному напрямі на 5 одиниць;
- у від’ємному напрямі на 2 одиниці;
- на 4 одиниці.
- Позначте на координатній прямій точки з координатами 4; 1,5; - 3 та точки, координати яких протилежні цим числам.
- Напишіть усі цілі числа, розташовані на координатній прямій між числами: 1) -5,8 і 2,2; 2) -178,4 та -171.
-
Виберіть серед чисел 8;0;-10;-12;
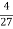 ; 5,4; -612;-3,1;2,91; -1001;
; 5,4; -612;-3,1;2,91; -1001;  ; 256:
; 256:
- Натуральні;
- Цілі;
- Додатні;
- Недодатні;
- Цілі від’ємні;
- Дробові невід’ємні.
- Записати 3 додатних і 4 від’ємних дробів із знаменником 9.
- Довжина одиничного відрізка координатної прямої дорівнює 2см. Чому дорівнює відстань між точками: 1) А(3) і В(7); 2) С(-5) і D(-2); 3) М(-3) і К(7)?
- Заповніть порожні клітинки в таблиці і позначте на координатній прямій точки, що мають своїми координатами числа таблиці:
|
x |
3 |
|
5 |
|
0 |
|
-6 |
|
–x |
|
4 |
|
-2 |
|
-1 |
|
- Виконайте вправу 897 ст. 172.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
- Накресліть координатну пряму і позначте на ній точки, що відповідають числам: 3; –2; 0; -6; 3,5; 1,5; -2,5.
- Записати 5 додатних і 4 від’ємних дробів із знаменником 13.
- Довжина одиничного відрізка координатної прямої дорівнює 2см. Чому дорівнює відстань між точками: 1) А(3) і В(7); 2) С(-2) і D(-8); 3) М(-5) і К(4)?
-
Вибрати серед чисел
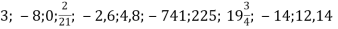
- цілі;
- невід’ємні;
- раціональні.
Урок №6
Математику вже тому вивчати потрібно,
що вона розум до ладу приводить
М. Ломоносов
Фронтальне опрацювання матеріалу
Модуль числа
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 2.12 блоку №6.
- Дайте відповіді на питання:
- Що називають раціональними числами?
- Які числа називаються цілими?
- Дайте визначення протилежних чисел.
-
 Що називають координатною прямою?
Що називають координатною прямою?
- Які числа називаються додатними, а які від’ємними?
- Що називають модулем числа?
-
Які властивості модуля вам відомі?
- На урок до нас завітав клоун Гоша. Допоможіть йому знайти карточки з числами, модулі яких рівні.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Виконайте вправи зі стор. 175 – 176:
918, 922, 924, 929, 930.
Урок №7
Хто шукає любов — провину ховає,
хто ж про неї повторює, розганяє друзів
Приповісті Соломонові 17:9
Фронтальне опрацювання матеріалу
Модуль числа
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 2.12 блоку №6.
- Дайте відповіді на питання:
- Що називають модулем числа?
- Як позначають модуль числа?
- Як знайти модуль додатного числа або 0?
- Як знайти модуль від’ємного числа?
- Чи може модуль деякого числа бути від’ємним?
- Якими є модулі двох протилежних чисел?
- Які числа називаються раціональними?
- Які числа називаються протилежними?
- Що називають координатною прямою?
Завдання 2.
Виконати усно вправи запропоновані вчителем.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Як може кішка зайти в підвал з одною головою, а вийти з двома?
Завдання 4.
Виконайте письмово вправи:
4.1. Обчисліть: ![]() .
.
4.2. Розташуйте числа 2,7; 4; -7,2; 0,9; - 2,3 у порядку зростання їх модулів.
Уроки №8, 9
Найвище призначення математики – знаходити
порядок у хаосі, який нас оточує.
Н. Вінтер (американський математик)
Фронтальне опрацювання матеріалу
Порівняння раціональних чисел
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези блоку №6.
- Дайте відповіді на питання:
- Які числа називаються раціональними?
- Які числа називаються від’ємними?
- Що називають координатною прямою?
- Дайте означення модулю числа.
- Які властивості модуля вам відомі?
- Як порівняти два числа за допомогою координатної прямої?
- Як порівняти додатні і від'ємні числа?
- Як порівняти від'ємні числа з 0?
- Яке з двох від'ємних чисел більше?
Завдання 2.
Назвіть, яке число більше:
1) -2 і 4;
2) -3 і -1;
3) 7 і -9;
4) -10 і 0;
5) -4 і -5.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
3.1. Розташуйте в порядку спадання числа:
![]()
![]()
![]()
3.2. Сполучити числа на малюнку попарно стрілками так, щоб кожна стрілка була спрямована від більшого числа до меншого.
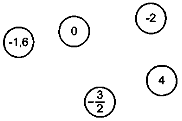
3.3. Які цифри можна записати замість *, щоб утворилася правильна нерівність:
![]()
3.4. Обчислити![]()
Завдання 4.
Виконайте вправи зі ст. 180 – 181:
956 (1, 3, 5, 7), 958, 960, 962.
Завдання 5.
Позначте на координатній прямій числа, модуль яких дорівнює 4; 8; 2,5; 0; 2.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
Виберіть серед чисел
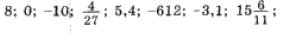
![]() 1) натуральні; 2) цілі; 3) додатні;
1) натуральні; 2) цілі; 3) додатні;
4) недодатні; 5) цілі від’ємні; 6) дробові невід’ємні.
-
Знайдіть модуль кожного з чисел:
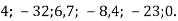
- Напишіть усі цілі числа, розташовані на координатній прямій між числами:
![]()
- Знайти значення виразу:
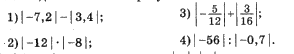
- Позначте на координатній прямій числа, модуль яких дорівнює 3; 5; 3,5; 5; 0.
-
Розташуйте числа у
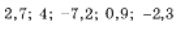 порядку спадання їх модулів.
порядку спадання їх модулів.
Урок №11
«Істинно чесний той, хто завжди
запитує себе, чи досить він чесний»
Сократ
Внутрішньопредметне узагальнення матеріалу
Раціональні числа
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 6.
- Дай письмово відповідь на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Письмово виконай вправи:
-
Записати числа, протилежні до чисел: 81; -74;
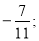 8,5.
8,5.
-
Порівняти числа: 1) -87 і 50; 2) 0 і -29; 3) -160 і -130; 4) -7,6 і – 6,7; 5)
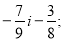 6)
6) 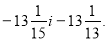
-
Обчислити значення виразу: 1)
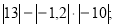 2)
2) 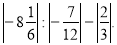
-
Яку цифру можна поставити замість зірочки, щоб утворилась правильна нерівність (розглянути всі можливі випадки):
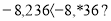
-
Розв’язати рівняння: 1)
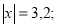 2)
2) 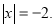
-
Знайти модулі чисел 78; -47; 684; 5,9;
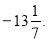
-
Записати числа -893; -1000;
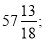 -62; 48,5 у порядку зростання їх модулів.
-62; 48,5 у порядку зростання їх модулів.
- Записати числа у порядку зростання: 109; -98; 89; -70,5; -15.
- Позначити на координатній прямій числа, модулі яких дорівнюють 3,5; 5; 8.
- Накреслити координатну пряму, взявши за одиничний відрізок 1см, і позначити на ній точки: 1) М (-3,5); 2) К (6,5); 3) N (4); 4) Р (-4).
Тема №7. Додавання і віднімання раціональних чисел
Урок №1

Додавання і віднімання раціональних чисел
«Де це можливо, рахуйте»
Френсіс Гальтон — англійський дослідник,
географ, антрополог, психолог і статистик
Питання
- Додавання раціональних чисел.
- Властивості додавання.
- Віднімання раціональних чисел.
- Розкриття дужок.
Література
Істер О.С. Математика: підручник для 6 класу, Київ: «Генеза», 2014. – §§38 – 42, стор. 185 – 210.
|
|
1. Додавання раціональних чисел |
|||
|
1.1
|
Щоб додати два від’ємних числа, достатньо додати їх модулі і перед отриманим числом записати знак «–». |
|
||
|
1.2 |
Сума двох протилежних чисел дорівнює нулю. |
|
||
|
1.3
|
Щоб додати два числа з різними знаками, достатньо від більшого модуля доданків відняти менший модуль і записати перед знайденим числом знак того доданка, модуль якого більший. |
|
||
|
|
2. Властивості додавання |
|||
|
2.4
|
Переставна властивість
Для будь-яких раціональних чисел
|
|
||
|
2.5
|
Сполучна властивість
Для будь-яких раціональних чисел
|
|
||
|
2.6
|
Для будь-якого раціонального числа
|
|
||
|
2.7 |
Якщо потрібно додати декілька чисел, серед яких є додатні і від’ємні, то можна спочатку додати окремо від’ємні числа, потім додатні і знайти суму чисел з різними знаками. |
|
||
|
|
3. Віднімання раціональних чисел |
|||
|
3.8
|
Щоб від одного числа відняти друге, достатньо до зменшуваного додати число, протилежне від’ємнику: |
|
||
|
4. Розкриття дужок |
||||
|
4.9 |
Щоб розкрити дужки, перед якими стоїть знак «+», треба не писати дужок і знак «+», що стоїть перед ними та записати всі доданки зі своїми знаками. |
|
||
|
4.10 |
Щоб розкрити дужки, перед якими стоїть знак «–», треба не писати дужки і знак «–», що стоїть перед ними, та записати всі доданки з протилежними знаками. |
|
||
Алгоритм додавання (віднімання) раціональних чисел

|
|
|
Однакові |
|
Різні |
|
|
||
|
Став той же знак |
|
Став знак, який стоїть перед більшим числом |
|
|
||
|
Додати |
|
Відняти |
Уроки №2,3
«Якщо людина живе тільки для себе,
єдине, чого вона заслуговує – презирства»
Цицерон, давньоримський політичний діяч
Фронтальне опрацювання матеріалу
Додавання від’ємних чисел
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.2 блоку № 7.
- Дай відповіді на питання:
- Які числа називаються від’ємними?
- Як додати два від’ємних числа?
- Чи можна при додаванні від’ємних чисел отримати нуль?
- Чи можна при додаванні від’ємних чисел отримати додатне число?
- Чи можна при додаванні від’ємних чисел отримати від’ємне число?
Завдання 2.
Гра «Вірю – не вірю»
Відповідь «вірю» – підніми праву руку, відповідь «не вірю» – руки не піднімай.
- Два числа, що відрізняються один від одного тільки знаками, називаються протилежними числами.
- Для кожного числа є два протилежних йому числа.
- Сума протилежних чисел дорівнює нулю.
- Модуль числа 0 дорівнює нулю.
- Модуль числа може бути від’ємним.
- Протилежні числа мають різні модулі.
- З двох від’ємних чисел менше те, модуль якого більший.
- Нуль менше будь-якого від’ємного числа.
- Нуль менше будь-якого додатного числа.
- Якщо до будь-якого числа додати нуль, то число не зміниться.
Завдання 3.
Усно виконай вправу 992, стор. 185 підручника.
 ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 4.
Виконай письмово вправи, стор. 186 підручника: 993 (1, 3, 7); 996 (1, 4).
Завдання 5.
Виконай письмово вправи, стор. 187 підручника: 1000; 1002 (2, 3, 4).
Завдання 6.
Виконай письмово вправи, стор. 187 - 188 підручника: 1006 (1, 5); 1008; 1010.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 7.
Виконай письмово вправи, стор. 188 підручника: 1011; 1014; 1017; 1018; 1019.
Уроки №4,5
«Якщо ти змудрів – то для себе змудрів»
Книга приповістей Соломонових 9:12
Фронтальне опрацювання матеріалу
Додавання двох чисел з різними знаками
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.3 блоку № 7.
- Дай відповіді на питання:
- Які числа називаються раціональними?
- Які числа називаються додатними, а які від’ємними?
- Що називають модулем числа?
- Як додати від’ємні числа?
- Як додати числа з різними знаками?
- Чому дорівнює сума протилежних чисел?
Завдання 2.
Усно виконай вправи, стор. 190 підручника: 1020, 1021, 1022.
Завдання 3.
Виконай завдання «Ланцюжок обчислень», запропоновані вчителем.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 4.
- Розглянь приклад 2, стор. 190 підручника.
- Користуючись розглянутим прикладом, виконай вправу 1023, стор. 190 підручника.
Завдання 5.
- Розглянь приклад 3, стор. 190 підручника.
- Користуючись розглянутим прикладом, виконай вправу 1026, стор. 191 підручника.
Завдання 6.
- Письмово виконай вправи, стор. 191 – 192 підручника: 1028; 1031; 1033; 1037 (самостійно).
- Усно виконай вправу 1030, стор. 191 підручника.
- Письмово виконай вправи, стор. 192 – 193 підручника: 1041; 1043 (1; 3; 5; 7; 9; 11); 1043 (2; 4; 6; 8; 10; 12 – самостійно)
Завдання 7.
Письмово виконай вправи, стор. 193 підручника: 1045 (1); 1045 (2 – самостійно); 1050.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 8.
Письмово виконай вправи, стор. 194 підручника: 1052; 1053; 1056.
Урок №6
«Слухай ради й картання приймай,
щоб мудрим ти став при своєму кінці»
Приповісті Соломонові 19:20
Фронтальне опрацювання матеріалу
Властивості додавання раціональних чисел
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1. – 2.7 блоку №7.
- Дай відповіді на питання:
- Які числа називаються раціональними?
- Як додати два від’ємних числа?
- Як додати два числа з різними знаками?
- Що є сумою протилежних чисел?
- Сформулюй переставну і сполучну властивість додавання.
- Чому дорівнює сума будь-якого числа з нулем?
- Як додавати числа, якщо серед них є декілька додатних і декілька від’ємних?
Завдання 2.
Усно виконай дії в таблицях:
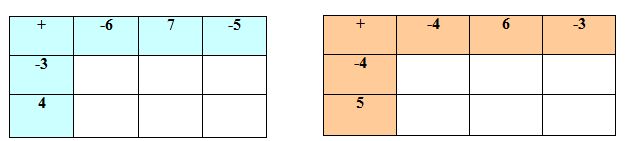
 ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
- Задача від Незнайка: Знайди суму всіх чисел від –499 до 501?
- Обчисли значення виразу за даним порадком дій:

- Склади числовий вираз та обчисли його значення:
1) до суми чисел –18,83 і 11,4 додати суму чисел –12,3 і 19,73.
2) до суми чисел –15,27 і 12,1 додати суму чисел 19,97 і -16,8.
- Виконай додавання, обираючи зручний порядок обчислень:
![]()
2) ![]()
3) ![]()
-
Спрости вираз
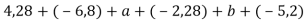 і знайди його значення при
і знайди його значення при 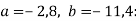
- Знайди суму всіх чисел від –4 до 5.
- Виконай додавання:
1) ![]()
2) ![]() ;
;
3) ![]() .
.
4) ![]()
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
- Знайди значення суми:
1) ![]() ;
;
2) ![]() ;
;
3) ![]()
4) ![]() .
.
- Виконай додавання:
1) ![]()
2) ![]()
3) ![]() ;
;
4) ![]() ;
;
5) ![]()
6) ![]()
7)![]() .
.
- Виконай обчислення, обираючи зручний порядок обчислення:
-
Спрости вираз
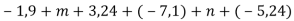 і знайди його значення при
і знайди його значення при
![]()
- Знайди суму всіх чисел від – 5 до 4.
-
Склади числовий вираз і обчисли його значення: до суми чисел
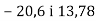
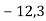
Урок №8
«Золоті яблука на срібнім тарелі це слово,
проказане часу свого»
Книга Приповістей Соломонових 25:11
Фронтальне опрацювання матеріалу
Віднімання раціональних чисел
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.8 блоку № 7.
- Дай відповіді на питання:
1. Чи завжди можливо виконати дію додавання?
2. Чи завжди можливо виконати дію віднімання?
3. Що означає відняти від одного числа інше?
4. Як називають компоненти дії віднімання?
5. Опиши алгоритм віднімання раціональних чисел.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Письмово виконай вправи, стор. 200 – 201 підручника: 1089, 1092, 1094.
Завдання 3. Пошук незнайомця
|
3.1.Визначення кольору шапки |
|
|
Обчисли:
|
Розшифровка: 54614 – коричневий 10457 - білий 74690 – жовтий 54138 - сірий 50901 - оранжевий 38195 – чорний 19046 – зелений 56349 – червоний |
|
3.2. Визначення кольору пальта |
|
|
Обчисли:
|
Розшифровка: 54614– коричневий 10457 - білий 74690 – жовтий 77438 - сірий 50901 - оранжевий 38195 – чорний 19046 – зелений 56349 – червоний |
|
3.3. Визначення віку героя портрета |
|
|
Щоб обчислити, скільки років герою, необхідно знайти суму чисел, які є коренями рівнянь:
1) |
|
|
3.4. Визначення імені героя |
|
|
Відповіді до прикладів указують номер букви в алфавіті, який додається:
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
А |
Б |
В |
Г |
Д |
Е |
Є |
Ж |
З |
И |
І |
Ї |
Й |
К |
Л |
М |
Н |
|
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
|
О |
П |
Р |
С |
Т |
У |
Ф |
Х |
Ц |
Ч |
Ш |
Щ |
Ю |
Я |
Ь |
Урок №9
«Слухайтесь ваших наставників та коріться їм…»
Послання апостола Павла до євреїв 13:17
Фронтальне опрацювання матеріалу
Віднімання раціональних чисел
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.8 блоку № 7.
- Встанови відповідність:
- Щоб додати два від’ємних числа, достатньо…
- Від’ємними називаються числа…
- Додатними називаються числа..
- Сума протилежних чисел дорівнює…
- Від перестановки доданків…
- Щоб додати два числа з протилежними знаками, треба…
- Сума будь-якого числа з нулем дорівнює…
- Щоб знайти різницю двох чисел, можна…
- Щоб до числа додати суму двох чисел…
А) нулю.
Б) тому самому числу.
В) до зменшуваного додати число, протилежне від’ємнику.
Г) сума не змінюється.
Д) знайти різницю їх модулів і перед результатом поставити знак числа з більшим модулем.
Е) додати їх модулі і перед отриманим числом поставити знак мінус.
Є) зі знаком мінус.
Ж) всі натуральні та дробові.
З) можна до суми першого і другого чисел додати третє число.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Усно виконай вправу 1091, стор. 201 підручника.
Завдання 3.
Письмово виконай вправи, стор. 202 підручника: 1103 (2; 4; 6); 1106; 1108.
Завдання 4.
Письмово виконай вправи, стор. 203 – 204: 1111; 1114 (2, 4); 1120.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 5.
Письмово виконай вправи, стор. 204: 1122 (1, 3, 5, 6) – скористайся наведеним зразком; 1125.
Уроки №10,11
«Математику не можна вивчати,
спостерігаючи як це робить сусід»
Айвен Нівен, американський математик
Фронтальне опрацювання матеріалу
Розкриття дужок
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези блоку № 7.
- Дай відповідь на питання:
- Які числа називаються раціональними?
- Як додати два від’ємних числа?
- Як відняти два раціональних числа?
- Як додати два числа різними знаками?
- Як додати числа, якщо серед них декілька додатних і декілька від’ємних?
- Як розкрити дужки, перед якими стоїть знак «+»?
- Яке число є сумою двох протилежних чисел?
- Які числа називаються протилежними?
- Як розкрити дужки, перед якими стоїть знак «-»?
Завдання 2.
Усно виконай вправу 1130, стор. 206 підручника.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконай письмово вправи, стор. 206 – 207 підручника: 1132, 1134 (1, 3, 5), 1138 (2, 4, 6), 1141, 1142.
Завдання 4.
Виконай самостійно вправи.
Розкрити дужки:
1 варіант
- - (5 – х) – 6у =
- а +( в – с) =
- - (25 + а )– 4в =
- - в – (5 – 6а) =
- - 8 + (х – 4у) =
- - а –( в + с) =
- - (5 – а) + 54в =
- -(в + 9) – 3а =
2 варіант
- - (z + ху) – 6у =
- - ( а + в) – с =
- 21 – (а – 66в) =
- - с – (49 + 3а) =
- - (9 – а) – 5в =
- (- а + в) – с=
- - (85 – а) – 404в =
- в – (10 + а) =
Завдання 5.
Виконай вправи, стор. 207 – 208 підручника: 1144 (1, 3, 5); 1148 (2, 4); 1146.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 6.
Виконай вправи, стор. 208 – 209 підручника: 1151; 1153.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
- Знайди різницю:
-
Знайди значення виразу:
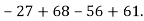
-
Розв’яжи рівняння:
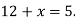
- Спрости вираз:
- Розкрий дужки і спрости вираз:
Урок №13
«Більше думай і тоді вирішуй»
Григорій Сковорода
Внутрішньопредметне узагальнення матеріалу
Додавання і віднімання раціональних чисел
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 7.
- Письмово дай відповідь на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
- Знайди помилку в обчисленнях:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Розв’яжи рівняння
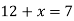
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Знайди значення виразу
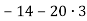
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Завдання 3.
Письмово виконай вправи:
-
Виконай додавання: 1)
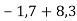
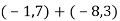 .
.
-
Розв’яжи рівняння: 1)
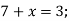
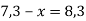
-
Бензин замерзає за температури
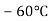
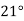
- Між Тернополем і Рівним є міста Кременець і Дубно. Відстань від Тернополя до Рівного дорівнює 158 км, від Кременця до Рівного – 80 км, від Кременця до Дубно – 39 км. Знайди відстань від Тернополя до Дубно.
-
Точка замерзання ртуті дорівнює
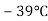
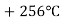
-
Розв’яжи рівняння, спочатку спростивши вираз у його лівій частині:
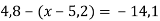 .
.
Тема №8. Множення і ділення раціональних чисел
Урок №1

Множення і ділення раціональних чисел
«Хто зневажає досягнення математики, той
завдає шкоди всій науці, бо той, хто не знає математики,
не може вивчати інші точні науки й не може пізнати світ»
Роджер Бекон, англійський філософ
Питання
- Множення раціональних чисел.
- Властивості множення. Коефіцієнт буквеного виразу.
- Подібні доданки та їх зведення
- Ділення раціональних чисел.
Література
Істер О.С. Математика: підручник для 6 класу, Київ: «Ґенеза», 2014, §§ 43 – 47, ст. 210 – 235.
|
1. Множення раціональних чисел |
||
|
1.1. |
Щоб помножити два числа з різними знаками, треба помножити їх модулі і перед отриманим добутком поставити знак “–“. |
|
|
1.2. |
Щоб помножити два від’ємних числа, треба помножити їх модулі. |
|
|
1.3. |
|
|
|
2. Властивості множення. Коефіцієнт буквеного виразу |
||
|
2.4. |
Переставна властивість множення
Для будь-яких раціональних чисел a і b виконується рівність: |
|
|
2.5 |
Сполучна властивість множення
Для будь-яких раціональних чисел a, b і с виконується рівність: |
|
|
2.6. |
Якщо вираз є добутком числа і однієї або кількох букв, то це число називають числовим коефіцієнтом (або просто коефіцієнтом). |
|
|
2.7. |
Розподільна властивість множення
Для будь-яких раціональних чисел |
|
|
2.8. |
Заміну виразу |
|
|
2.9. |
Заміну виразу
|
|
|
3. Подібні доданки та їх зведення |
||
|
3.10. |
Доданки, що мають спільну буквену частину, називають подібними доданками. |
|
|
3.11. |
Щоб звести подібні доданки, треба додати їх коефіцієнти і отриманий результат помножити на спільну буквену частину. |
|
|
4. Ділення раціональних чисел |
||
|
4.12. |
Щоб поділити два числа з різними знаками, треба модуль діленого поділити на модуль дільника і перед отриманим числом поставити знак «–». |
|
|
4.13. |
Щоб поділити два від’ємних числа, треба модуль діленого поділити на модуль дільника. |
|
|
4.14. |
Властивості ділення:
|
|
Схема визначення знака добутку раціональних чисел
![]()
![]()
![]()
![]()
Уроки №2,3
«Успіх означає вміння терпіти одну
поразку за іншою, не втрачаючи волі до перемоги»
Ві́нстон Че́рчилль, державний діяч Великої Британії
Фронтальне опрацювання матеріалу
Множення раціональних чисел
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.3 блоку № 8.
- Дай відповідь на питання:
- Як помножити два числа з різними знаками?
- Як помножити два від’ємних числа?
- Чому дорівнює добуток чисел, якщо хоча б один із множників дорівнює нулю?
Завдання 2.
Спираючись на тези блоку, усно виконай вправи, стор.212 підручника: 1157, 1158.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконай вправи, стор. 212 – 214 підручника: 1159, 1167 (1, 3, 5, 7), 1170, 1172, 1181.
Завдання 4.
Самостійно виконай вправу 1161, стор. 212 підручника.
Завдання 5.
Виконай вправу 1185, стор. 214 підручника.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 6.
- Усно виконай вправу:
Дано числа ![]()
- Модулі цих чисел.
- Яке із чисел більше?
- Два цілих числа, розташованих між ними.
- Два числа, які менше даних чисел.
- Два числа, які більше даних чисел.
- Суму даних чисел.
- Різницю даних чисел.
-
Добуток даних чисел.
- Письмово виконай вправи, стор. 215 підручника: 1187, 1189.
Урок №4
«У житті людини головне – Праця»
Василь Сухомлинський,
український педагог
Фронтальне опрацювання матеріалу
Переставна і сполучна властивості множення. Коефіцієнт буквеного виразу
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 2.6 блоку № 8.
- Усно дай відповіді на питання:
- Як помножити два числа з різними знаками?
- Як помножити два від’ємних числа?
- Коли добуток дорівнює нулю?
- Сформулюй переставну властивість множення.
- Сформулюй сполучну властивість множення.
- Що називають коефіцієнтом?
-
Як називається число
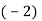 у виразі
у виразі 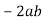
Завдання 2.
Усно виконай вправи:
2.1. Обчисли:
-
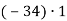 ;
;
-
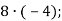
-
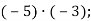
-

-
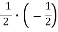
-
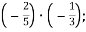
-
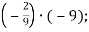
-
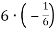
2.2. Не виконуючи множення, знайди знак добутку:
-
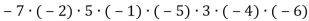 ;
;
-
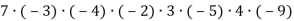 .
.
2.3. Назви коефіцієнт виразу:
![]() .
.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконай вправи, стор. 218 – 219 підручника: 1200; 1203; 1206; 1209.
Завдання 4.
Письмово виконай вправи, стор. 219 підручника: 1211 (2; 4); 1213 (1; 3).
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 5.
Виконай вправи:
-
(усно) Чому дорівнює добуток усіх цілих чисел від
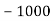
- Письмово виконай вправу 1217, стор. 220.
-
Розв'яжи рівняння: 1)
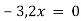
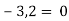
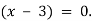
Урок №5
«Дурень той, хто кидає справу на півдорозі і
дивиться, роззявивши рот, з боку, що з усього цього вийде»
Фрідріх Шиллер, німецький поет
Фронтальне опрацювання матеріалу
Розподільна властивість множення
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.9 блоку № 8.
- Усно дай відповіді на питання:
- Які числа називаються раціональними?
- Як помножити два від’ємних числа?
- Як помножити два числа з різними знаками?
- Сформулюй переставну і сполучну властивості множення.
- Сформулюй розподільну властивість множення.
- Що називають розкриттям дужок?
- Що називають винесенням спільного множника за дужки?
Завдання 2.
Виконай усно вправи, стор. 222 підручника: 1221, 1222.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконай письмово вправи, стор. 222 – 224 підручника: 1228 (2, 4, 6, 8); 1230 (1, 3, 5, 7); 1235 (1, 3, 5), 1236 (2, 4).
Завдання 4.
Виконай письмово вправи, стор. 224 - 225 підручника: 1240; 1242 (2, 4, 6); 1244.
Уроки №6,7
«Люди бувають нерозумними,
нелогічними та егоїстичними — і все ж люби їх!»
Мати Тереза
Фронтальне опрацювання матеріалу
Подібні доданки та їх зведення
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.11 блоку № 8.
- Усно дай відповіді на питання:
- Як помножити два від’ємних числа?
- Як помножити два числа з різними знаками?
- Сформулюй переставну і сполучну властивості множення.
- Сформулюй розподільну властивість множення.
- Що називають розкриттям дужок?
- Що називають винесенням спільного множника за дужки?
- Що називають подібними доданками?
- Як звести подібні доданки?
Завдання 2.
Виконай усно вправу 1248, стор. 226 підручника.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
- Розглянь приклади 2, 3, стор. 226 підручника.
- Користуючись розглянутими прикладами, виконай письмово вправи, стор. 226 – 227 підручника: 1251 (1, 3, 5, 7); 1254 (2, 4); 1257; 1262.
Завдання 4.
Виконай письмово вправи, стор. 227 – 228 підручника: 1264; 1266 (1,3); 1268.
Завдання 5.
- Розглянь приклад 4, стор. 226 підручника.
- Письмово виконай вправи, стор. 228 підручника: 1270; 1272; 1274.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 6.
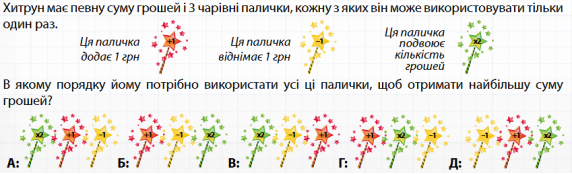

 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
- Знайди добуток:
-
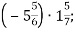
-
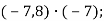
-
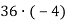
-
Обчисли зручним способом:
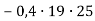
-
Зведи подібні доданки:
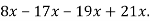
-
Виконай дії:
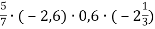 .
.
-
Спрости вираз:
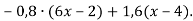
-
Виконай дії:
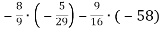 .
.
-
Знайди значення виразу
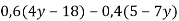 при
при 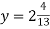 ;
;
Уроки №9,10
«Хто землю свою обробляє, той насититься хлібом,
а хто за марнотним женеться, насититься вбогістю»
Книга приповістей Соломонових 28:19
Фронтальне опрацювання матеріалу
Ділення раціональних чисел
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори блок № 8.
- Усно дай відповідь на питання:
- Як поділити два числа з різними знаками?
- Як поділити два від’ємних числа?
- Сформулюй властивості ділення.
- Як помножити два числа з різними знаками?
- Які вирази називаються подібними?
- Що називають коефіцієнтом?
- Як звести подібні доданки?
- Що називають розкриттям дужок?
- Сформулюй властивості множення раціональних чисел.
- Що називають винесенням спільного множника за дужки?
- Усно розв’яжи вправи 1285, 1287, 1288, стор 231 підручника.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
- (Усно) Встанови відповідність між виразами та їх значеннями:

- Знайди значення виразу:
- Знайди значення виразу:
-
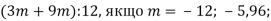
-
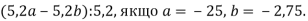
- Знайди значення виразу:
Завдання 3.
Письмово розв’яжи вправи, стор. 232 – 233 підручника: 1294 (1, 3, 5, 7), 1298, 1300 (2, 4, 6).
Завдання 4.
Письмово розв’яжи вправу 1304, стор. 233 підручника.
Завдання 5.
Письмово розв’яжи вправи, стор. 234 підручника: 1309, 1311 (1, 3), 1313, 1315; 1317; 1319.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
- Виконай дії:
-
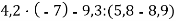 ;
;
-
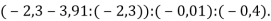
- Від добутку чисел 1,325 і –4 відніми частку чисел 70,28 і 14.
-
Розв’яжи рівняння і знайди значення виразу
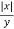 :
:
![]() ;
;
Урок №12
«Хто зневажає досягнення математики, той
завдає шкоди всій науці, бо той, хто не знає математики,
не може вивчати інші точні науки й не може пізнати світ»
Роджер Бекон, англійський філософ
Внутрішньопредметне узагальнення матеріалу
Множення і ділення раціональних чисел
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 8.
- Письмово дай відповідь на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
- Знайди помилку в обчисленнях:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Обчисли
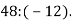
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
Розв’яжи рівняння:
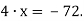
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Завдання 3.
Письмово виконай вправи:
-
Знайди добуток: 1)
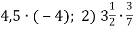 .
.
-
Виконай дії:
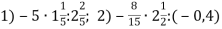 .
.
-
Виконай дії:
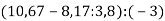 .
.
-
Знайди добуток коренів рівнянь
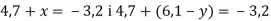 .
.
-
Спрости вираз
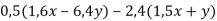 і обчисли його значення, якщо
і обчисли його значення, якщо 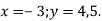
Тема №9. Рівняння
Урок №1

Рівняння
«Не знаючи від’ємних чисел,
неможливо знайти корені всіх рівнянь»
А.Г. Мерзляк
Питання
- Рівняння.
- Властивості рівнянь
- Розв’язування задач за допомогою рівнянь
Література
Істер О.С. Математика: підручник для 6 класу, Київ: «Генеза», 2014, §§ 48 – 50, стор. 235 – 255.
|
||||||||||
|
1.1 |
Рівність, яка містить змінну, називається рівнянням. |
|
||||||||
|
1.2 |
Розв’язок рівняння (корінь) – це значення змінної при якому рівняння перетворюється у правильну рівність. |
|
||||||||
|
||||||||||
|
2.3 |
Корені рівняння не зміняться, якщо його обидві частини помножити або поділити на одне й те ж саме відмінне від нуля число. |
|
||||||||
|
2.4 |
Корені рівняння не зміняться, якщо деякий доданок перенести з однієї частини рівняння в іншу, змінивши при цьому його знак на протилежний. |
|
||||||||
|
2.5 |
Загальна схема розв’язування рівнянь:
|
Розв’язати рівняння: 4(x – 3) – 12x = 3(2 – x) + 7; 4x – 12 – 12x = 6 – 3x + 7; –8x – 12 = 13 – 3x; –8x + 3x = 13 + 12; –5x = 25; x = 25 : (–5); x = –5. |
||||||||
|
||||||||||
|
3.6 |
План розв’язування задач за допомогою рівнянь:
|
|||||||||
|
На двох полицях було порівну книжок. Після того як з першої полиці взяли 8 книжок, а з другої – 24 книжки, то на першій полиці залишилось у 3 рази більше книжок, ніж на другій. Скільки книжок було на кожній полиці спочатку?
Відповідь: 32 книги. |
||||||||||
Уроки №2 – 4
«І я бачив – нема чоловікові кращого,
як ділам своїм радіти, бо це доля його!»
Книга Еклезіястова 3: 22
Фронтальне опрацювання матеріалу
Розв’язування рівнянь. Основні властивості рівнянь
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.5 блоку №9.
- Усно дай відповідь на питання:
- Що називають рівнянням?
- Що називають коренем рівняння?
- Сформулюй основні властивості рівнянь.
- За якою схемою розв’язують рівняння?
Завдання 2.
Виконай усно вправи, стор. 238 підручника: 1324; 1326; 1327.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконай вправи стор. 238 – 240 підручника: 1328, 1330, 1332, 1334 (1, 3, 5), 1335; 1338 (2, 4, 6), 1341 (1, 3, 5).
Завдання 4.
Виконай письмово вправи стор. 240 підручника: 1345 (1,3), 1347 (2, 3); 1348 (2; 4).
Завдання 5.
-
Розв’яжи рівняння:
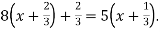
-
Розв’яжи рівняння:
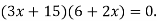
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 6.
Виконай письмово вправи стор. 241 підручника: 1352 (1); 1354; 1355.
Уроки №5 – 7
«Кожен розумний за мудрістю
робить, а безумний глупоту показує»
Книга приповістей Соломонових 13:16
Фронтальне опрацювання матеріалу
Розв’язування задач за допомогою рівнянь
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори блок № 9.
- Дай відповіді на запитання:
- Що називають рівнянням?
- Що називають коренем рівняння?
- Сформулюй основні властивості рівняння.
- Коли добуток кількох множників дорівнює нулю?
Завдання 2.
- Розглянь приклади розв’язування тестових задач 1, 2, стор. 242 – 243 підручника.
- Усно дай відповідь на питання:
- За яким планом розв’язують задачі за допомогою рівнянь?
- За чим перевіряють правильність розв’язання задачі?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Усно склади рівняння до задачі:
- Сума двох чисел дорівнює 48. Одне з них у 3 рази більше за друге. Знайди ці числа.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Різниця двох чисел дорівнює 26. Одне з них у 2 рази менше, ніж друге. Знайди ці числа.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Син у 3 рази молодший від батька. Скільки років батькові, якщо він старший за сина на 24 роки?
|
А |
Б |
В |
Г |
|
|
|
|
|
- Автомобіль до першої зупинки пройшов шлях у 6 разів довший ніж до другої. Який шлях він долав до першої і до другої зупинки, якщо до першої він пройшов шлях на 45 км більший, ніж до другої?
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 4.
Письмово виконай вправи, стор. 244 – 246 підручника: 1372, 1376, 1386.
Завдання 5.
- Розглянь приклад розв’язування вправи 1390, стор. 246 підручника.
- Користуючись розглянутим прикладом, письмово виконай вправи, стор. 246 – 247 підручника: 1392, 1395, 1400.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 6.
Письмово розв’яжи задачі:
- У ливарному цеху розрахували, що якщо з чавуну, який є, вилити 150 деталей, то залишиться 600 кг чавуну, а якщо вилити 134 таких самих деталі, то залишиться 1496 кг чавуну. Чому дорівнює маса однієї деталі? Скільки чавуну є в цеху?
- Бабуся підрахувала, що в неї не вистачає 4 цукерки, щоб дати кожному онукові по 3 цукерки, а якщо вона дасть кожному по 2 цукерки, то залишиться 3 цукерки. Скільки онуків у бабусі? Скільки було у бабусі цукерок?
Завдання 7.

 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
Розв’яжи рівняння:
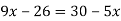
-
Розв’яжи рівняння:
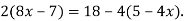
- Периметр прямокутника дорівнює 11,2 дм, а одна з його сторін на 2,4 дм більша за сусідню. Знайди сторони прямокутника.
- У Сашка в колекції було в 4 рази більше солдатиків, ніж у Юрка. Коли Сашко подарував Юркові 18 солдатиків, то в обох хлопчиків солдатиків стало порівну. Скільки солдатиків було в кожного хлопчика спочатку?
Уроки №9 – 11
«Не бійся й не лякайся, бо з тобою
Господь, Бог твій, у всьому, де ти будеш ходити»
Книга Ісуса Навина 1:9
Фронтальне опрацювання матеріалу
Розв’язування вправ на всі дії з раціональними числами
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори блоки № 7 – 9.
- Дай відповіді на питання:
- Які числа називаються раціональними?
- Як додати два числа з різними знаками?
- Як додати два від’ємних числа?
- Як знайти різницю двох раціональних чисел?
- Як помножити два від’ємних числа?
- Як помножити два числа різними знаками?
- Сформулюй правило ділення двох від’ємних чисел.
- Як поділити два числа з різними знаками?
- Сформулюй правила розкриття дужок.
- Що називають рівнянням?
- Що називають коренем рівняння?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Усно виконай вправи, стор. 250 підручника: 1414; 1415; 1418; 1419.
Завдання 3.
Письмово виконай вправи, стор. 250 – 251 підручника: 1461(1; 3; 5; 7); 1420 (2; 4; 6; 8); 1426; 1427.
Завдання 4.
- Письмово виконай вправи, стор. 252 – 254 підручника: 1433 (1; 3; 5); 1440 (2); 1446; 1450.
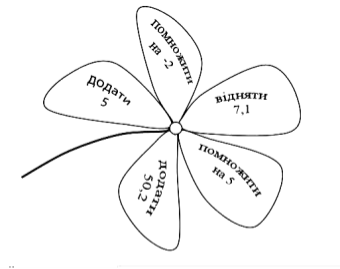
- Самостійно відшукайте число, заховане у пелюстках квітки. Для цього виконайте дії з раціональними числами. Почніть виконання з числа:
І варіант – 3,05,
ІІ варіант – 4,03.
- Одного року в англійському графстві Кемберленд знялася буря, сильний вітер виривав дерева з корінням, утворюючи воронки. У одній із таких воронок жителі виявили якусь чорну речовину. Назва цієї речовини зашифрована діями з раціональними числами. Розв’яжіть дані приклади, результати їх замініть буквами, використовуючи шифр «числовий вираз – буква». Складіть слово і прочитайте його.
![]()
![]()
![]()
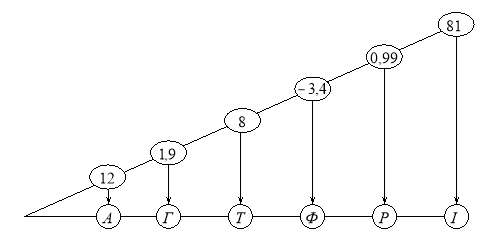
![]()
![]()
![]()
Шматочками графіту чабани стали мітити овець, купці робили надписи на ящиках. Дізнайтеся, в якому році трапилося почута подія. Для цього розв’яжіть приклад, відповідь якого – рік події.
![]()
Отже, графіт був знайдений у 1565 році. Перші олівці мали недолік – вони бруднили пальці і швидко ламалися. Шматочки графіту стали обмотувати тасьмою чи тканиною, а для міцності змішували з сіркою, сурмою, смолою. Пізніше стали додавати глину і все поміщали в піч. Сучасний олівець з’явився в кінці XVІІІ століття. Зараз будь – який малюнок спочатку виконується олівцями з графітовими стержнями.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 5.
 5.1. Гілки смородини витримують температуру до - 5˚С, а після загартування вони можуть витримувати температуру, на 58˚С нижчу. Яку температуру можуть витримати гілки смородини після загартування?
5.1. Гілки смородини витримують температуру до - 5˚С, а після загартування вони можуть витримувати температуру, на 58˚С нижчу. Яку температуру можуть витримати гілки смородини після загартування?
5.2. Під час перебування космонавта у відкритому космосі температура з сонячного боку його скафандра становила +140˚С, а з тіньового - -130˚С. Яка різниця температур між сонячною і тіньовою боками скафандра?
5.3. Коли мороз сягає - 40˚С, температура тіла песця - +38˚С, а білої куріпки - +43˚С. На скільки температура тіла песця і куріпки вищі від температури повітря?
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
Виконай дії:
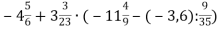 .
.
-
Обчисли:
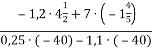 .
.
-
Спрости вираз
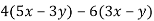 і обчисли його значення при
і обчисли його значення при 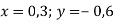
Урок №13
«Хто зневажає досягнення математики, той
завдає шкоди всій науці, бо той, хто не знає математики,
не може вивчати інші точні науки й не може пізнати світ»
Роджер Бекон, англійський філософ
Внутрішньопредметне узагальнення матеріалу
Рівняння
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 9.
- Письмово дай відповідь на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
- Якщо в рівнянні 5x + 8 = 7 доданок 8 перенести в праву частину, то одержимо рівняння ...
|
А |
Б |
В |
Г |
|
5x = 7 + 8 |
5x = 7 · 8 |
5x = –7 · 8 |
5x = 7 – 8 |
- Яке з наведених чисел є коренем рівняння –5x = 20?
|
А |
Б |
В |
Г |
|
|
4 |
–4 |
|
- Одне з чисел на 7,8 більше, ніж друге. Якщо менше з чисел позначити через x, то більше з чисел буде дорівнювати ...
|
А |
Б |
В |
Г |
|
7,8x |
x + 7,8 |
x – 7,8 |
7,8 – x |
Завдання 3.
Письмово виконай вправи:
- У двох бригадах працює 84 чоловіки, причому у першій — на 14 чоловік більше, ніж у другій. Скільки чоловік у кожній бригаді?
- На першій ділянці було у 4 рази більше кущів малини, ніж на другій. Якщо з першої ділянки пересадити на другу 30 кущів, то на обох ділянках кущів стане порівну. Скільки кущів малини було на кожній ділянці спочатку?
- У першій бригаді було в 5 раз більше робітників, ніж у другій. Після того, як з першої бригади перевели 4 чоловіки у другу, у першій стало людей у два рази більше, ніж у другій. Скільки робітників було у кожній бригаді спочатку?
- Розв’яжи рівняння: 1) –7x = 42; 2) 10x – 8 = 0.
- Розв’яжи рівняння: 4(x – 1,5) + 4 = x – 5.
-
Розв’яжи рівняння:
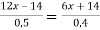 .
.
Тема №10. Паралельні і перендикулярні прямі. Координатна площина
Урок №1

Паралельні і перпендикулярні прямі. Координатна площина
«Хто ума набуває, кохає той душу свою,
а хто розум стереже, той знаходить добро»
Книга приповістей Соломонових 19:8
Питання
- Перпендикулярні і паралельні прямі.
- Координатна площина.
Література
Істер О. С. Математика: Підручник для 6 класу. – Київ: Генеза, 2014 рік, §§ 51 - 54, стор. 255 – 284
|
||
|
1.1 |
Дві прямі, що мають одну спільну точку називають прямими, що перетинаються. Їх спільну точку називають точкою перетину. |
|
|
1.2 |
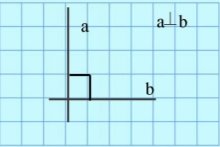
Прямі, що перетинаються під прямим кутом, називаються перпендикулярними прямими. |
|
|
1.3 |
Відрізки (або промені), що лежать на перпендикулярних прямих, називаються перпендикулярними відрізками (або променями).
|
|
|
1.4. |
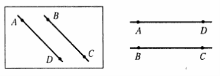
Дві прямі на площині, які не перетинаються, називають паралельними. |
|
|
1.5. |
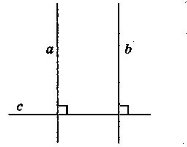
Якщо дві прямі, які лежать в одній площині, перпендикулярні до третьої, то вони паралельні.
|
|
|
1.6 |
Відрізки (або промені), що лежать на паралельних прямих, називаються паралельними відрізками (або променями). |
|
|
||
|
2.7 |
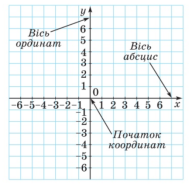
Дві перпендикулярні координатні прямі, проведені так, що їх початки відліку збігаються, називаються осями координат.
|
|
|
2.8 |
Точка перетину осей координат називається початком координат. |
|
|
2.9 |
Горизонтальну вісь називають віссю абсцис і позначають буквою |
|
|
2.10 |
Вертикальну вісь називають віссю ординат і позначають буквою |
|
|
2.11 |
Вісь абсцис і вісь ординат утворюють прямокутну систему координат. |
|
|
2.12 |
Площину, на якій задано прямокутну систему координат, називають координатною площиною. |
|
|
2.13 |
Координатні осі розбивають площину на чотири частини, які називають координатними чвертями. |
|
|
2.14 |
Записуючи координати точки, абсцису завжди ставлять на перше місце, а ординату – на друге. |
А (4; – 5) 4 – абсциса (координата х); – 5 – ордината (координата у). |
|
2.15 |
Початок координат має координати (0;0). |
|
Урок №2
«Кожна людина народжується для якогось діла»
Е. Хемінгуей
Фронтальне опрацювання матеріалу
Перпендикулярні прямі
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.3 блоку № 10.
- Дай відповіді на питання:
- Коли кажуть, що прямі перетинаються?
- Які прямі називаються перпендикулярними?
-
За допомогою яких інструментів можна побудувати перпендикулярні прямі?
- Наведи з довкілля приклади перпендикулярних прямих.
Завдання 2.
Виконай усно вправи, стор. 257 підручника: 1463; 1464.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконай вправи, стор. 258 – 259 підручника: 1465, 1467, 1470, 1471, 1473, 1474.
Урок №3
«Урок, який я засвоїв і якому
слідую все життя, полягав у тому,
що треба намагатися, і намагатися,
і знову намагатися - але ніколи не здаватися!»
Річард Бренсон,британський підприємець-міліардер
Фронтальне опрацювання матеріалу
Паралельні прямі
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.6 блоку № 10.
- Дай відповіді на питання:
- Коли кажуть, що прямі перетинаються?
- Які прямі називаються перпендикулярними?
- Які відрізки або промені називаються перпендикулярними?
- Які прямі називаються паралельними?
- Сформулюй властивість двох прямих, перпендикулярних до третьої прямої.
- Які відрізки або промені називаються паралельними?
Завдання 2.
Виконай усно вправи, стор. 261 підручника: 1479; 1480.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
- Розглянь приклад на стор. 260 підручника.
- Користуючись розглянутим прикладом, письмово виконай вправу 1482, стор. 261 підручника.
Завдання 4.
Письмово виконай вправи, стор. 261 – 262 підручника: 1484; 1486; 1488.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 5.

Уроки №4,5
«І ввесь людський рід Він з одного
створив, щоб замешкати всю поверхню землі,
і призначив окреслені доби й границі замешкання їх»
Дії святих апостолів 17:26
Фронтальне опрацювання матеріалу
Координатна площина
І. Робота над засвоєнням понять, означень, правил
Завдання 1.
- Повтори блок № 10.
- Усно дай відповідь на питання:
- Які прямі називаються перпендикулярними?
- Які прямі називаються паралельними?
- Що називають осями координат?
- Що називають початком координат?
- Як називають і позначають координатні осі?
- Що таке прямокутна система координат?
- Що називається координатною площиною?
- Як називаються частини площини, на які її розбивають координатні осі?
- Як записують координати точки?
- Які координати має початок координат?
Завдання 2.
Усно виконай вправу:
Зображено пари координатних прямих, які перетинаються. Які із цих пар не утворять координатну площину? Чому?
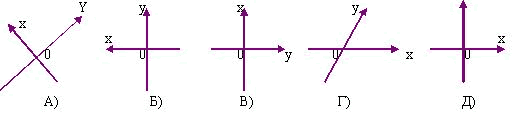
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконай вправи, стор.266 підручника: 1498, 1502, 1503, 1507, 1509.
Завдання 4.
Усно виконай вправи:
- Встав пропущені слова у тексті:
- Точка К (-7; 3) лежить у … координатній чверті, а точка М (5; -2) – у… чверті.
-
Відстань від точки А (-3; -6) до осі абсцис дорівнює ..., а до осі ординат - ....
- Заповни таблицю, спіймавши потрібних метеликів, та згадай прізвище великого французького математика:
|
(-3;8) |
(4;-5) |
(-9;-3) |
(5;6) |
(-3;-10) |
(10;10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Завдання 5.
Письмово виконай вправи, стор.269 підручника: 1518, 1520, 1524.
Завдання 6.
Письмово виконай вправи, стор.271 підручника: 1531, 1532.
Урок №6
«усе Він прегарним зробив свого часу»
Книга Еклезіаста 3:11
Фронтальне опрацювання матеріалу
Координатна площина
І. Робота над засвоєнням понять, означень, правил
Завдання 1.
- Повтори блок № 10.
- Усно дай відповідь на питання:
- Які прямі називаються перпендикулярними?
- Які прямі називаються паралельними?
- Що називають осями координат?
- Що називають початком координат?
- Як називають і позначають координатні осі?
- Що таке прямокутна система координат?
- Що називається координатною площиною?
- Як називаються частини площини, на які її розбивають координатні осі?
- Як записують координати точки?
- Які координати має початок координат?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
Письмово виконай вправу:
Ваше завдання прослідкувати за ходом жучка. Він повзе по листочку в напрямках, що вказують стрілки, починаючи з точки, обведеної колом. Знайди координати відмічених точок і запиши їх.
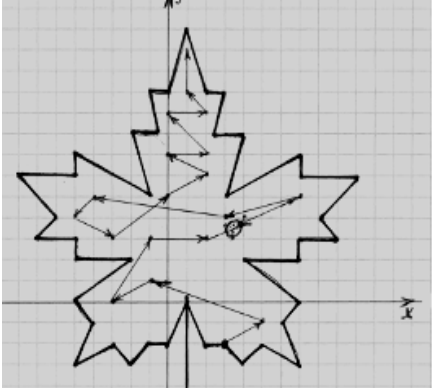
ІІІ. Відпрацювання умінь та навичок розв’язування нестандартних вправ
Завдання 3.
Побудуй малюнки на координатній площині за запропонованими точками (презентація вчителя).
Уроки №7,8
«…ліпша бо мудрість за перли»
Книга приповістей Соломонових 8:11
Фронтальне опрацювання матеріалу
Приклади графіків залежностей між величинами
І. Робота над засвоєнням понять, визначень, правил
Завдання 1.
- Повторити блок № 10.
- Усно дати відповідь на питання:
- Як називаються дві перпендикулярні координатні прямі, які перетинаються в початку відліку?
- Як називають площину, на якій задано систему координат?
- Як називають і позначають координатні прямі?
- Як записують координати точки?
- Де знаходяться точки, абсциси яких дорівнюють нулю?
- Де знаходяться точки, ординати яких дорівнюють нулю?
- Які координати має початок координат?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
Письмово виконай вправи, стор. 275 підручника: 1539, 1541.
Завдання 3.
Усно виконай вправи, стор. 276 підручника: 1543; 1547.
Завдання 4.
Побудуй графік зміни температури протягом доби за такими даними:
1)
|
t, год |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
|
t° C |
4 |
1 |
– 1 |
– 3 |
– 1 |
5 |
6 |
5 |
5 |
4 |
3 |
2 |
1 |
2)
|
t, год |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
|
t° C |
2 |
1 |
0 |
– 2 |
0 |
2 |
3 |
4 |
3 |
2 |
2 |
1 |
0 |
Завдання 5.
Письмово виконай вправи, стор. 278 підручника: 1550, 1552.
 Готуємось до індивідуального опрацювання
Готуємось до індивідуального опрацювання
-
На координатній площині познач точки:
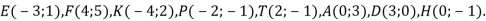
-
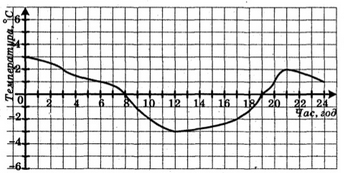 На рисунку зображено графік зміни температури повітря протягом доби. Користуючись цим графіком, установи:
На рисунку зображено графік зміни температури повітря протягом доби. Користуючись цим графіком, установи:
- якою була температура повітря о 3 год., о 17 год., о 24 год.?
-
о котрій годині температура повітря була
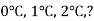
- якою була найнижча температура і о котрій годині?
-
Задано три вершини прямокутника ABCD:
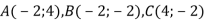 .
.
- Накресли цей прямокутник.
- Визнач і запиши координати четвертої вершини.
- Побудувавши на координатній площині дані точки, з’єднай їх, щоб утворився малюнок:
1) (2; – 3), (2; – 2), (4; – 2), (4; – 1), (3; 1), (2; 1), (1; 2), (0; 0), (- 3; 2), (- 4; 5), (0; 8), (2; 7), (6; 7), (8; 8), (10; 6), (10; 2), (7; 0), (6; 2), (6; – 2), (5; – 3), (2; – 3).
2) (4; – 3), (4; – 5), (3; – 9), (0; – 8), (1; – 5), (1; – 4), (0; – 4), (0; – 9), (- 3; – 9), (- 3; – 3),
(- 7; – 3), (- 7; – 7), (- 8; – 7), (- 8; – 8), (- 11; – 8), (- 10; – 4), (- 11; – 1), (- 14; – 3), (- 12; – 1), (- 11;2), (- 8;4), (- 4;5).
3) Очі: (2; 4), (6; 4).
Урок №10
«…усе Він прегарним зробив свого часу»
Книга Еклезіаста 3:11
Внутрішньопредметне узагальнення матеріалу
Паралельні і перпендикулярні прямі. Координатна площина
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 10.
- Письмово дай відповідь на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
 Усно виконай вправи:
Усно виконай вправи:
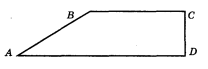
- Паралельними є відрізки (мал.1):
|
А |
Б |
В |
Г |
|
BC i CD |
BC i AD |
AD i AB |
BC i BA |
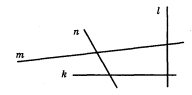
- Вкажи перпендикулярні прямі (мал.2):
|
А |
Б |
В |
Г |
|
|
|
|
|
-
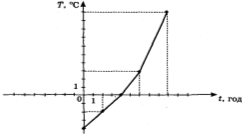 Користуючись графіком, знайди: 1) температуру повітря, якщо час дорівнює 2 год. 2) час доби, якщо температура повітря дорівнює
Користуючись графіком, знайди: 1) температуру повітря, якщо час дорівнює 2 год. 2) час доби, якщо температура повітря дорівнює 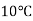
|
|
А |
Б |
В |
Г |
|
1) |
|
|
|
|
|
2) |
|
|
|
|
Завдання 3.
Письмово виконай вправи:
- Накресли тупий кут АВС. Познач між сторонами кута точку D і проведи через цю точку пряму: 1) паралельну стороні ВС; 2) перпендикулярну до сторони ВА.
- Назви 4 точки на координатній площині, в яких: 1) абсциса і ордината протилежні числа; 2) ордината у 2 рази більша від абсциси.
-
Побудуй пряму
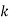
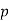
- Побудуй точки на координатній площині і отримай малюнок:
(2;5), (8;5), (9;6), (9;3), (8;1), (6;2), (7;1), (1;1), (1;0), (10;-1), (13;0), (14;3), (14;1), (13;-1), (10;-2), (10;-3), (12;-5), (11;-8), (9;-8), (10;-6), (8;-5), (8;-7), (7;-8), (5;-8), (6;-7), (6;-5), (3;-5), (3;-8), (1;-8), (0;-5), (-1;-7), (-3;-8), (-3;3), (-4;3), (-4;-3), (-5;-4), (-7;-4), (-7;4), (-6;6), (-4;6), (-4;8), (-2;9), (0;9), (2;7), (2;5)
Тема №11. Повторення матеріалу, вивченого протягом року
Уроки №1, 2
«…ліпша бо мудрість за перли»
Книга приповістей Соломонових 8:11
Внутрішньопредметне узагальнення матеріалу за рік
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блоки № 1 – 10.
- Усно дай відповідь на питання:
- Що називають відношенням?
- Що називають пропорцією?
- Сформулювати основну властивість пропорції.
- Що таке відсоток?
- Як знайти відсотки від числа?
- Як знайти число за його відсотками?
- Які числа називаються додатними, від’ємними, раціональними?
- Сформулювати правила додавання раціональних чисел.
- Як знайти різницю двох чисел?
- Сформулювати правила множення раціональних чисел.
- Сформулювати правила ділення раціональних чисел.
- Які вирази називаються подібними?
- Як звести подібні доданки?
- Що називають рівнянням?
- Що називають коренем рівняння?
- Сформулювати властивості рівнянь.
- Що називається осями координат, початком координат?
- Як називають і позначають координатні осі?
- Що називають системою координат?
- Що називають координатною площиною?
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
-
Обчисли:
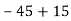
|
А |
Б |
В |
Г |
|
– 60 |
– 30 |
30 |
60 |
-
Зведи подібні доданки:
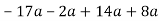
|
А |
Б |
В |
Г |
|
|
|
|
|
- В саду 80 дерев, з них 40 % – яблуні. Скільки яблунь в саду?
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 3.
Письмово виконай вправи:
-
Порівняти числа: 1) -87 і 50; 2) 0 і -29; 3) -160 і -130; 4) -7,6 і – 6,7; 5)
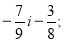 6)
6) 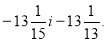
-
Обчислити значення виразу: 1)
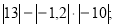 2)
2) 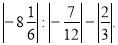
-
Записати всі цілі розв’язки нерівності
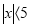 .
.
-
Розв’яжи рівняння:
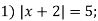 2)
2) 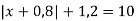 .
.
-
Виконай дії:
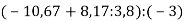 .
.
-
Знайди добуток коренів рівнянь
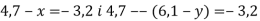 .
.
- На трьох полицях 170 книг. На третій полиці в 2 рази більше книжок, ніж на другій, а на другій — на 10 книжок менше, ніж на першій. Скільки книжок на кожній полиці?
-
Розв’язати рівняння
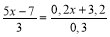 .
.
Завдання 4.
-
Розв’яжи рівняння:
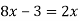
-
Знайди значення виразу:
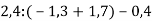
-
Знайди невідомий член пропорції:
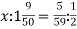 .
.
- Розв’яжи за допомогою рівняння.
В одному ящику було в 2 рази більше помідор, ніж в другому. Після того як з першого ящика пересипали у другий 4 кг помідор, у першому залишилось в 5 разів менше помідор, ніж стало у другому. Скільки помідор було в кожному ящику спочатку?
-
Учень прочитав книгу за три дні. Першого дня він прочитав
 книги, другого – 30% книги, а третього – решту 27 сторінок. Скільки сторінок в цій книзі?
книги, другого – 30% книги, а третього – решту 27 сторінок. Скільки сторінок в цій книзі?
- Побудувати малюнок на координатній площині:
- (-6;-1), (-5;-4), (-2;-6), (-1;-4), (0;-5), (1;-5), (3;-7), (2;-8), (0;-8), (0;-9), (3;-9), (4;-8), (4;-4), (5;-6), (8;-4), (8;0), (6;2), (4;1), (0;1), (-2;2), (-6;-1), (-10;-2), (-13;-4), (-14;-7), (-16;-9),(-13;-7), (-12;-10), (-13;-14),(-10;-14), (-10;-13), (-9;-13), (-10;-9), (-5;-9), (-5;-15), (-2;-15),(-2;-13). (-2;-10), (-1;-10), (-1;-11), (-2;-13), (0;-15), (2;-11), (2;-9);
- (- 9; 6), (- 5; 9), (- 5; 10), (- 4; 10), (- 4; 4), (- 3; 4), (0; 7), (2; 4), (4; 7), (7; 4), (9; 3), (9; 1), (8; - 1), (8; 1), (7; 1), (7; - 7), (6; - 7), (6; - 2), (4; - 1), (- 5; - 1), (- 5; - 7),(- 6; - 7), (- 6; 5), (- 7;5), (- 8; 4), (- 9; 4), (- 9; 6).
![]()


про публікацію авторської розробки
Додати розробку