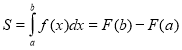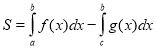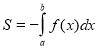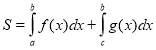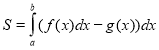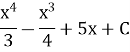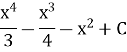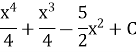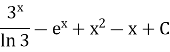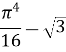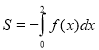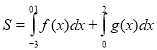Навчально-методичний матеріал для самостійної роботи студентівза темою "Площа криволінійної трапеції, площа фігури."
1
Міністерство освіти і науки України
Білгород-Дністровський державний аграрний технікум
МАТЕМАТИКА
Розділ «Інтеграл та його застосування»
Навчально-методичні матеріали для самостійної роботи студентів
за темою «Площа криволінійної трапеції, площа фігури»
Номінація: інноватика в організації самостійної роботи
2017
Укладач - Купцова Оксана Володимирівна, викладач математики, спеціаліст першої категорії
Рецензент – Донцова Тетяна Петрівна, викладач математики, спеціаліст вищої категорії
Даний навчально-методичний матеріал містить різноманітні види завдань для самостійної роботи студентів з розділу «Інтеграл та його застосування» за темою «Площа криволінійної трапеції. Площа фігури». Самостійні роботи № 1, № 2 та № 3 можна застосовувати з метою перевірки знань, закріплення умінь та навичок обчислення первісних та інтегралів, а також з метою повторювання пройденого матеріалу перед вивченням теми «Площа криволінійної трапеції. Площа фігури». Самостійні роботи № 4, № 5 та № 6 складені з метою навчання, тренування та закріплення знань, умінь та навичок обчислювати площі криволінійних трапецій та різноманітних фігур,застосовувати формулу Ньютона - Лейбніца.
Розглянуто і схвалено на засіданні методичної ради
Протокол № 8 від 13.04.2017
Зміст
Індивідуальні завдання за темою «Інтеграл та його застосування»
Вступ.
Сучасні вчені-педагоги вже багато років розробляють нові програми, підручники, які направлені на вдосконалення учбового процесу та розвиток мислення студентів та учнів шкіл.
Проблема формувань умінь самостійної роботи є актуальною для викладачів усіх предметів, у тому числі, і для викладачів математики. Для її розв’язку потрібно застосовувати різноманітні види самостійної роботи, форми організації і контролю самостійної роботи студентів, забезпечити самостійну роботу студента достатньою кількістю методичних матеріалів.
Самостійна навчальна діяльність – це організована викладачем діяльність студентів, направлена на виконання учбового завдання у спеціально відведений час. Її метою є формування та розвиток навичок та умінь, закріплення, систематизація знань, поглиблення та розширення вже отриманих знань.
Самостійна робота студента формує необхідний об’єм та рівень знань, навичок і умінь для розв’язання задач, виробляє психологічну установку на систематичне поповнення своїх знань, умінь орієнтуватися в потоці наукової інформації.
Основний недолік традиційної системи навчання складається у тому, що викладачі реалізують лише одну функцію знань – інформаційну, але забувають про не менш значиму розвиваючу функцію. Вона передбачає вчити студентів мислити, шукати і знаходити відповіді на запитання, добувати нові знання.
Увага до проблеми розвитку самостійності студентів поясняється тим, що вона відіграє вагому роль не тільки в справі освіти, але і в підготовці студентів до їх майбутньої трудової діяльності. Вона необхідна для будь-якої людини незалежно від того, в якої сфері вона буде працювати після закінчення учбового закладу.
1. Основні теоретичні відомості за темою «Визначений інтеграл. Площа криволінійної трапеції. Площа фігури».
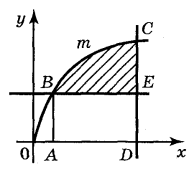
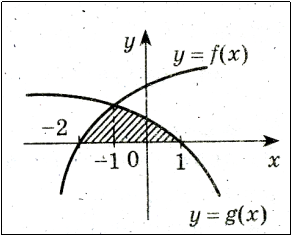
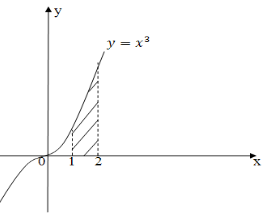
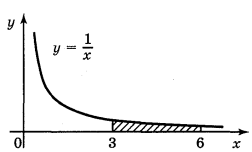
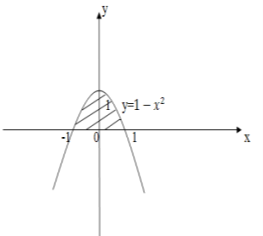
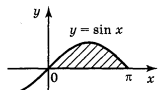
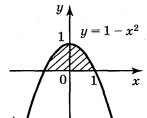
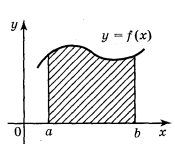 Криволінійною трапецією називається фігура, обмежена графіком неперервної функції у = f(x), яка не змінює знак на відрізку [а; b], прямимиx = а, х = b і відрізком [а; b] ( див. рисунок)
Криволінійною трапецією називається фігура, обмежена графіком неперервної функції у = f(x), яка не змінює знак на відрізку [а; b], прямимиx = а, х = b і відрізком [а; b] ( див. рисунок)
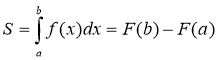
Ця формула називається формулою Ньютона - Лейбніца. Вона правильна для будь-якої неперервної на відрізку [а; b] функції f(x), пов'язує поняття інтеграла й первісної для даної функції, є правилом обчислення інтегралів.
Для зручності запис різниціF(b) - F(a) прийнято скорочено позначати![]() . При такому позначенні формула Ньютона – Лейбніца набирає вигляду:
. При такому позначенні формула Ньютона – Лейбніца набирає вигляду:
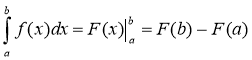
Із властивостей первісної і формули Ньютона - Лейбніца випливають основні властивості інтеграла.
- Інтеграл суми (різниці) функцій дорівнює сумі (різниці) інтегралів :
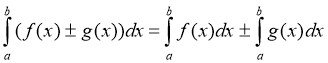 .
.
2) Постійний множник можна виносити за знак інтеграла:
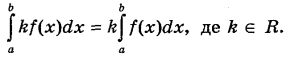
3) Якщо с є [а; b], то
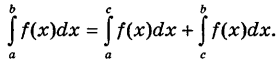
4)
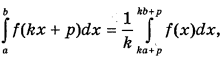 де ρ є R, k
де ρ є R, k
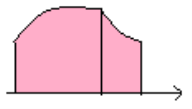
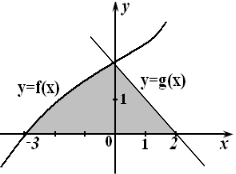
Обчислення площ плоских фігур.
|
|
Площа криволінійної трапеції
|
|
|
Обчислення площ
|
|
|
|
|
|
|
|
|
|
2. Самостійна робота №1.
Пояснювальна записка.
Самостійна робота №1 має в своєму складі 6 варіантів одного рівня складності, що дає змогу поставити студентів однієї групи в рівні умови.
В складі кожного варіанта всього 12 завдань з яких 7 тестових завдань. Це завдання початкового і середнього рівнів складності на обчислення нескладних, у своєї більшості табличних первісних та визначених інтегралів. Одне завдання на встановлення відповідності функції та її первісної. Останні 4 завдання достатнього та високого рівня, які потребують більш глибоких знань, умінь та навичок обчислення інтегралів, застосування формули Ньютона - Лейбніца.
Метою даної роботи є перевірка знань, закріплення умінь та навичок обчислення первісних та інтегралів, а також повторювання пройденого матеріалу перед вивченням теми «Площа криволінійної трапеції. Площа фігури».
Орієнтовний час виконання самостійної роботи 20-25 хвилин.
Варіанти завдань
Варіант 1.
1. Яка з функцій є первісною для функції ![]() ? (0,5 бали)
? (0,5 бали)
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
2. Яка з функцій є такою, що ![]() ?(0,5 бали)
?(0,5 бали)
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
3. Укажіть для функції ![]() первісну, графік якої проходить через точку М(0;1)? (0,5 бали)
первісну, графік якої проходить через точку М(0;1)? (0,5 бали)
а) ![]() ; в)
; в) ![]() ;
;
б)![]() ; г)
; г) ![]() .
.
4. Обчисліть інтеграл  .(1 бал)
.(1 бал)
а) 1; в) -1;
б) 0; г) -2.
5. Обчисліть інтеграл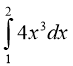 .(1 бал)
.(1 бал)
а) 4; б) 16; в) 8; г) 15.
6. Одна з первісних функції у = 2х має вигляд: (0,5 бали)
а) 2х2 б) ![]() в)
в) ![]() г) х2
г) х2
7. Загальний вигляд первісних для у = cosx : (0,5 бали)
а) cos х + С![]() б) sinx в) – соs х + С г) sіn х + С
б) sinx в) – соs х + С г) sіn х + С
8. Обчислити визначений інтеграл: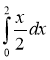 ; (1 бал)
; (1 бал)
9. Поставити у відповідність функцію та її первісну:
- f(х) = х2 а) 0,5 cos2х ( 0,5 бали)
-
f(х) = - sin2х б)
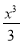 ( 0,5 бали)
( 0,5 бали)
- f(х) = 2х5 в) 3 sinх( 0,5 бали)
-
f(х) = 3cos х г)
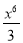 ( 0,5 бали)
( 0,5 бали)
10.Обчислити невизначений інтеграл: (1,5 бали)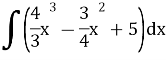
11.Обчислити визначений інтеграл: (1,5бали)
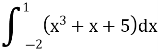
12.Обчислити визначений інтеграл: (1,5бали)
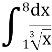
Варіант 2.
1. Яка з функцій є первісною для функції ![]() ? (0,5 бали)
? (0,5 бали)
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
2. Яка з функцій є такою, що ![]() 1? (0,5 бали)
1? (0,5 бали)
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
3. Укажіть для функції ![]() первісну, графік якої проходить через точку М(0;-1)? (0,5 бали)
первісну, графік якої проходить через точку М(0;-1)? (0,5 бали)
а) ![]() ; в)
; в) ![]() ;
;
б)![]() ; г)
; г) ![]() .
.
4. Обчисліть інтеграл 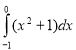 . (1 бал)
. (1 бал)
а) ![]() ; в) 1;
; в) 1;
б)![]() ; г) -3.
; г) -3.
5.Обчисліть інтеграл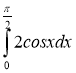 . (1 бал)
. (1 бал)
а) 1; б) 4; в) 0; г) 2.
6. Одна з первісних функції f(х) = - 2sinх має вигляд : (0,5 бали)
а) 2cos х ![]() б) sinx в) – 2соs х г) - sіn х
б) sinx в) – 2соs х г) - sіn х
7. Загальний вигляд первісних для у = ах : (0,5 бали)
а) ах +С б) ах в) ![]() +C г) ахlna+C
+C г) ахlna+C![]()
8.Обчислити визначений інтеграл: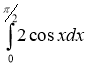 (0,5 бали)
(0,5 бали)
9. Поставити у відповідність функцію та її первісну:
- f(х) = х3 а) -0,25 cos4х (0,5 бали)
-
f(х) = sin4х б)
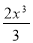 (0,5 бали)
(0,5 бали)
- f(х) = 2х2 в) -2sinх (0,5 бали)
-
f(х) = -2cos х г)
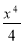 (0,5 бали)
(0,5 бали)
10.Обчислити невизначений інтеграл: (1,5бали)
![]()
11.Обчислити визначений інтеграл: (1,5бали)
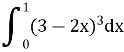
12.Обчислити визначений інтеграл: (2 бали)
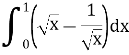
Варіант 3.
1. Яка з функцій є первісною для функції ![]() ? (0,5 бали)
? (0,5 бали)
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
2. Яка з функцій є такою, що![]() ? (0,5 бали)
? (0,5 бали)
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
3. Укажіть для функціїf(х) = х2 первісну, графік якої проходить через точку М(-1;3)? (0,5 бали)
а) ![]() ; в)
; в) ![]() ;
;
б)![]() ; г)
; г) ![]() .
.
4. Обчислити інтеграл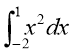 (1 бал)
(1 бал)
а) -3 б) 2 в) -2 г) 3
5.Обчисліть інтеграл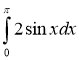 .(1 бал)
.(1 бал)
а) 1; б) 4; в) 0; г) -2.
6. Одна з первісних функції у = 3х2 має вигляд (0,5 бали)
а) ![]() б) х3 в)
б) х3 в) ![]() г)
г)![]()
7. Загальний вигляд первісних для у=xα:![]() (0,5 бали)
(0,5 бали)
а) αхα-1+C а) ![]() в)
в) ![]() +C г)
+C г)![]() +C, α≠-1
+C, α≠-1
8.Обчислити визначений інтеграл:![]()
![]() (0,5 бали)
(0,5 бали)
9. Поставити у відповідність функцію та її первісну:
1. f(х) = х+4 а) -3cosх(0,5 бали)
2. f(х) = 2cos2х б) ![]() +4х (0,5 бали)
+4х (0,5 бали)
3. f(х) = х5 в)sin2х (0,5 бали)
4. f(х) = 3sin х г) ![]() (0,5 бали)
(0,5 бали)
10.Обчислити невизначений інтеграл: (1,5 бали)
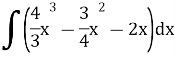
11.Обчислити визначений інтеграл: (1,5 бали)
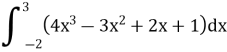
12.Обчислити визначений інтеграл: (2 бали)
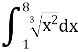
Варіант 4.
1. Яка з функцій є первісною для функції ![]() ? (0,5 бали)
? (0,5 бали)
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
2. Яка з функцій є такою, що![]() ? (0,5 бали)
? (0,5 бали)
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
3. Укажіть для функції f(х) = sin х первісну, графік якої проходить через точку М(π;-1)? (0,5 бали)
а) ![]() ; в)
; в) ![]() ;
;
б)![]() ; г)
; г) ![]() .
.
4. Обчислити інтеграл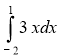 (1 бал)
(1 бал)
а) ![]() б) 4 в)
б) 4 в) ![]() г) -4
г) -4
5.Обчисліть інтеграл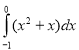 . (1 бал)
. (1 бал)
а) ![]() ; б) 1; в)
; б) 1; в)![]() ; г) -3.
; г) -3.
6. Одна з первісних функції у = х має вигляд: (0,5 бали)
а) 2х2 б) ![]() в)
в) ![]() г) х2
г) х2
7. Загальний вигляд первісних для у = е![]() є: (0,5 бали)
є: (0,5 бали)
а) е![]() б)
б) ![]() + С в)
+ С в) ![]() + С г) е
+ С г) е![]() + С
+ С
8. Обчислити визначений інтеграл:![]() ; (0,5 бали)
; (0,5 бали)
9. Поставити у відповідність функцію та її первісну:
1. f(х) = -sin2х а) 0,5 cos2х (0,5 бали)
2. f(х) = 2х5 б) ![]() (0,5 бали)
(0,5 бали)
3. f(х) = х2 в)3 sinх (0,5 бали)
4.f(х) = 3cos х г) ![]() (0,5 бали)
(0,5 бали)
10.Обчислити невизначений інтеграл: (1,5 бали)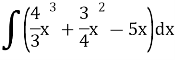
11.Обчислити визначений інтеграл: (1,5бали)
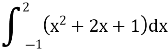
12.Обчислити визначений інтеграл: (2 бали)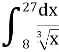
Варіант 5.
1. Яка з функцій є первісною для функції ![]() ? (0,5 бали)
? (0,5 бали)
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
2. Яка з функцій є такою, що![]() ? (0,5 бали)
? (0,5 бали)
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
3. Укажіть для функції f(x)=![]() первісну, графік якої проходить через точку М(0;-6)? (0,5 бали)
первісну, графік якої проходить через точку М(0;-6)? (0,5 бали)
а)F(x)=![]() ; в) F(x)=
; в) F(x)=![]() ;
;
б) F(x)=![]() ; г).F(x)=x+1.
; г).F(x)=x+1.
4. Обчисліть інтеграл 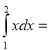 (1 бал)
(1 бал)
а) 1 б) 1![]() в) 3 г) – 1
в) 3 г) – 1
5. Обчисліть інтеграл 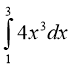 . (1 бал)
. (1 бал)
а) 80; б) 16; в) 8; г) 15.
6. Одна з первісних функціїу = х2має вигляд: (0,5 бали)
а) ![]() б) х3 в)
б) х3 в) ![]() г)
г)![]()
7. Загальний вигляд первісних для у = cosx :![]() (0,5 бали)
(0,5 бали)
а) sinx б) cosx+C в) sinx+C г) - sinx+C![]()
8.Обчислити визначений інтеграл:; 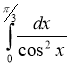 . (0,5 бали)
. (0,5 бали)
9. Поставити у відповідність функцію та її первісну:
1. f(х) = х2 а) ![]() (0,5 бали)
(0,5 бали)
2. f(х) = -sin2х б)![]() (0,5 бали)
(0,5 бали)
3. f(х) = 2х5 в)3 sinх (0,5 бали)
4. f(х) = 3cos х г) 0,5 cos2х (0,5 бали)
10.Обчислити невизначений інтеграл: (1,5 бали)
![]()
11.Обчислити визначений інтеграл: (1,5бали)
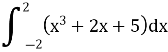
12.Обчислити визначений інтеграл: (2 бали)
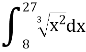
Варінт 6.
1. Яка з функцій є первісною для функції ![]() ? (0,5 бали)
? (0,5 бали)
а) ![]() ; б)
; б) ![]() ;
;![]()
в) ![]() ; г)
; г) ![]() .
.
2. Яка з функцій є такою, що![]() ? (0,5 бали)
? (0,5 бали)
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
3. Укажіть для функції ![]() первісну, графік якої проходить через точку М(0;1)? (0,5 бали)
первісну, графік якої проходить через точку М(0;1)? (0,5 бали)
а) ![]() ; в) F(x)= sinx-2
; в) F(x)= sinx-2
б)![]() ; г). ) F(x)= sinx+1
; г). ) F(x)= sinx+1
4. Обчисліть інтеграл 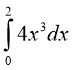 . (1 бал)
. (1 бал)
а) 4; в) 16;
б) 8; г) -4.
5.Обчисліть інтеграл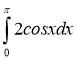 . (1 бал)
. (1 бал)
а) 1; б) 4; в) 0; г) -2.
6. Одна з первісних функції y =![]() має вигляд: (0,5 бали)
має вигляд: (0,5 бали)
а) y = ![]() г)
г) ![]() .
.
7. Загальний вигляд первісних для у = ![]() : (0,5 бали)
: (0,5 бали)
а) lnx +C б) ![]() + C в) ln
+ C в) ln![]() + С г)
+ С г) ![]() + C
+ C
8.Обчислити визначений інтеграл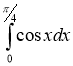 :(0,5 бали)
:(0,5 бали)
9. Поставити у відповідність функцію та її первісну:
- f(х) = sin4х а) -0,25 cos4х (0,5 бали)
-
f(х) = х3 б)
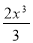 (0,5 бали)
(0,5 бали)
- f(х) = 2х2 в) -2sinх (0,5 бали)
-
f(х) = -2cos х г)
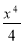 (0,5 бали)
(0,5 бали)
10. Обчислити невизначений інтеграл: (1,5 бали)
![]()
11.Обчислити визначений інтеграл: (1,5 бали)
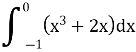
12. Обчислити визначений інтеграл:(2 бали)
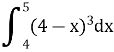
Ключі відповідей
Варіант 1.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
г |
б |
в |
б |
г |
г |
г |
1 |
|
9 |
10 |
11 |
12 |
||||
|
1б, 2а, 3г,4в |
|
9 |
4,5 |
||||
Варіант 2.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
а |
г |
г |
а |
г |
а |
в |
2 |
|
9 |
10 |
11 |
12 |
||||
|
1г, 2а, 3б, 4в |
- |
10 |
- |
||||
Варіант 3
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
в |
а |
г |
г |
б |
б |
г |
0,5 |
|
9 |
10 |
11 |
12 |
||||
|
1б, 2в, 3г, 4а |
|
36 |
18,6 |
||||
Варіант 4
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
в |
а |
а |
в |
в |
б |
г |
2 |
|
9 |
10 |
11 |
12 |
||||
|
1а, 2г, 3б, 4в |
|
9 |
7,5 |
||||
Варіант 5
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
в |
в |
в |
б |
а |
г |
в |
|
|
9 |
10 |
11 |
12 |
||||
|
1б, 2г, 3а, 4в |
|
20 |
130,8 |
||||
Варіант 6
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
в |
а |
б |
в |
в |
а |
в |
|
|
9 |
10 |
11 |
12 |
||||
|
1а,2г, 3б, 4в |
|
-1 |
- |
||||
3. Самостійна робота №2.
Пояснювальна записка.
Самостійна робота №2 має в своєму складі 6 варіантів одного рівня складності, що дає змогу поставити студентів однієї групи в рівні умови.
В складі кожного варіанта є всього 3 завдання : перше завдання достатнього рівня на обчислення первісної, графік якої проходить через дану точку,друге та третє завдання на застосування правил обчислення первісних та невизначених інтегралів достатнього та високого рівня.
Метою даної роботи є перевірка знань, закріплення умінь та навичок обчислення первісних та інтегралів, а також повторювання пройденого матеріалу перед вивченням теми «Площа криволінійної трапеції. Площа фігури».
Орієнтовний час виконання самостійної роботи 20 хвилин.
Варіанти завдань
Варіант 1
1. Для функції f(x) = х4 знайдіть первісну, графік якої проходить через точку А(-1; 0). (4 бали)
2. Знайдіть загальний вигляд первісних для функцій: (4 бали)
a) f(x)=(7 – 3х)5; б) f(x) = 2х5 - 5х2
3. Знайдіть невизначені інтеграли: (4 бали)
a) 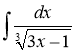 ; б)
; б) 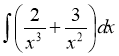 .
.
Варіант 2
1. Для функції f(x) =![]() знайдіть первісну, графік якої проходить через точку А(0; 1). (4 бали)
знайдіть первісну, графік якої проходить через точку А(0; 1). (4 бали)
2. Знайдіть загальний вигляд первісних для функцій: (4 бали)
a)f(x)= ![]() +
+![]() б)f(x) = е2х-1.
б)f(x) = е2х-1.
3. Знайдіть невизначені інтеграли: (4 бали)
a) ![]() ; б)
; б) ![]() .
.
Варіант 3
1. Для функції f(x) = sin x знайдіть первісну, графік якої проходить через точку А(π; 2). (4 бали)
2. Знайдіть загальний вигляд первісних для функцій: (4 бали)
a) f(x)=![]() -
-![]() . б) f(x)=
. б) f(x)=![]() +10x
+10x
3. Знайдіть невизначені інтеграли: (4 бали)
a)![]() ; б)
; б) 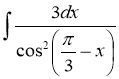 .
.
Варіант 4
1. Для функції f(x) =![]() знайдіть первісну, графік якої проходить через точку А
знайдіть первісну, графік якої проходить через точку А![]() . (4 бали)
. (4 бали)
2. Знайдіть загальний вигляд первісних для функцій: (4 бали)
a) f(x) =103х-1 - 2cos 6x б) f(x)=2ex +3cosx
3. Знайдіть невизначені інтеграли: (4 бали)
a) 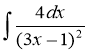 ; б)
; б) 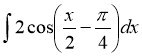 .
.
Варіант 5
1. Для функції f(x) = 3х2знайдіть первісну, графік якої проходить через точку А(0; 1). (4 бали)
2. Знайдіть загальний вигляд первісних для функцій: (4 бали)
a) f(x) = cos 2x + sin3х; б) f(x) =![]() .
.
3. Знайдіть невизначені інтеграли: (4 бали)
a) ![]() ; б)
; б) ![]() .
.
Варіант 6
1. Для функції f(x) = 4х3знайдіть первісну, графік якої проходить через точку А(0; 1). (4 бали)
2. Знайдіть загальний вигляд первісних для функцій: (4 бали)
a) f(x) =![]() ; б) f(x) =
; б) f(x) =![]() .
.
3. Знайдіть невизначені інтеграли: (4 бали)
a) ![]() ; б)
; б) ![]() .
.
Ключі відповідей
Варіант 1
|
1 |
2 а |
2б |
3а |
3б |
|
|
|
|
|
|
Варіант 2
|
1 |
2 а |
2б |
3а |
3б |
|
|
|
|
|
|
Варіант 3
|
1 |
2 а |
2б |
3а |
3б |
|
F(x)= -cosx+1 |
3tgx+5ctgx+C |
|
3 |
-3tg( |
Варіант 4
|
1 |
2 а |
2б |
3а |
3б |
|
F(x)=tgx-2 |
|
2 |
- |
4sin( |
Варіант 5
|
1 |
2 а |
2б |
3а |
3б |
|
F(x)= |
|
- |
|
tg(3x-1)+C |
Варіант 6
|
1 |
2 а |
2б |
3а |
3б |
|
F(x)= |
|
|
|
sin( |
4. Самостійна робота №3.
Пояснювальна записка.
Самостійна робота №3 має в своєму складі 6 варіантів одного рівня складності, що дає змогу поставити студентів однієї групи в рівні умови.
В складі кожного варіанта є 6 завдань на застосування правил обчислення інтегралів та на застосування формули Ньютона -Лейбніца. Усі завдання достатнього рівня складності. Особлива увага приділяється умінню застосовувати формулу інтеграла для степеневої функції.
Метою даної роботи є тренування, закріплення умінь та навичок обчислення інтегралів, а також повторювання пройденого матеріалу перед вивченням теми «Площа криволінійної трапеції. Площа фігури».
Орієнтовний час виконання самостійної роботи 20-25 хвилин.
Варіанти завдань
Варіант 1
Обчислити інтеграли:
1) 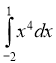 ; (2 бали) 2)
; (2 бали) 2) 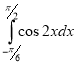 ; (2 бали)
; (2 бали)
3) ![]() ; (2 бали) 4)
; (2 бали) 4) 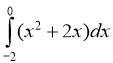 ; (2 бали)
; (2 бали)
5)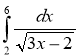 ; (2 бали) 6)
; (2 бали) 6) 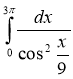 (2 бали)
(2 бали)
Варіант 2
Обчислити інтеграли:
1)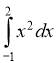 ; (2 бали) 2)
; (2 бали) 2) 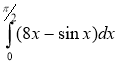 (2 бали)
(2 бали)
3) 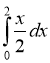 ; (2 бали) 4)
; (2 бали) 4)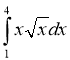 ; (2 бали)
; (2 бали)
5)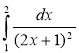 ; (2 бали) 6)
; (2 бали) 6) 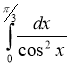 .(2 бали)
.(2 бали)
Варіант 3
Обчислити інтеграли:
1) 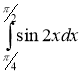 ; (2 бали) 2)
; (2 бали) 2) ![]() ; (2 бали)
; (2 бали)
3) 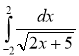 ; (2 бали) 4)
; (2 бали) 4) 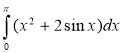 ; (2 бали)
; (2 бали)
5)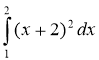 (2 бали) 6)
(2 бали) 6)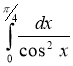 ; (2 бали)
; (2 бали)
Варіант 4
Обчислити інтеграли:
1) 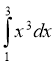 ; (2 бали) 2)
; (2 бали) 2) 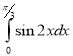 ; (2 бали)
; (2 бали)
3) ![]() ; (2 бали) 4)
; (2 бали) 4) 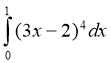 ; (2 бали)
; (2 бали)
5)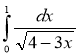 ; (2 бали) 6)
; (2 бали) 6)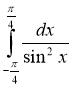 .(2 бали)
.(2 бали)
Варіант 5
Обчислити інтеграли:
1) 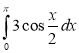 ; (2 бали) 2)
; (2 бали) 2) 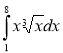 ; (2 бали)
; (2 бали)
3) ![]() ; (2 бали) 4)
; (2 бали) 4) 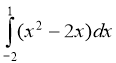 ; (2 бали)
; (2 бали)
5)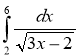 ; (2 бали) 6)
; (2 бали) 6) 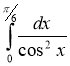 .(2 бали)
.(2 бали)
Варіант 6
Обчислити інтеграли:
1) 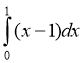 ; (2 бали) 2)
; (2 бали) 2) 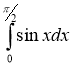 ; (2 бали)
; (2 бали)
3) ![]() ; (2 бали) 4)
; (2 бали) 4) 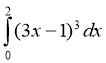 ; (2 бали)
; (2 бали)
5)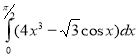 ; (2 бали) 6)
; (2 бали) 6) 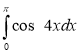 ; (2 бали)
; (2 бали)
Ключі відповідей
Варіант 1.
|
1 |
2 |
3 |
4 |
5 |
6 |
|
6,6 |
|
|
-1 |
1 |
|
Варіант 2.
|
1 |
2 |
3 |
4 |
5 |
6 |
|
3 |
Π-1 |
1 |
12,4 |
|
|
Варіант3.
|
1 |
2 |
3 |
4 |
5 |
6 |
|
- |
0,9 |
2 |
|
12 |
1 |
Варіант 4.
|
1 |
2 |
3 |
4 |
5 |
6 |
|
20 |
|
|
2,2 |
|
-2 |
Варіант 5.
|
1 |
2 |
3 |
4 |
5 |
6 |
|
6 |
54 |
6 |
|
|
|
Варіант 6.
|
1 |
2 |
3 |
4 |
5 |
6 |
|
- |
1 |
-2 |
52 |
|
0 |
5. Самостійна робота №4.
Пояснювальна записка.
Самостійна робота №4 має в своєму складі 6 варіантів одного рівня складності, що дає змогу поставити студентів однієї групи в рівні умови.
В складі кожного варіанта є всього 4 завдання : перше завдання початкового рівня на повторення загального вигляду первісних, друге – на уміння записувати формулу для обчислення площі фігури, третє та четверте завдання достатнього та високого рівня тому, що потребують вміння обчислювати площі плоских фігур, обмежених графіками функцій за допомогою визначеного інтегралу.
Метою даної роботи є навчання, тренування , закріплення умінь та навичок обчислення площ криволінійних трапецій та фігур.
Орієнтовний час виконання самостійної роботи 30 хвилин.
Варіанти завдань.
Варіант 1.
1. Вставте пропущені вирази: (2 бали)
|
х7 |
|
? |
|
cos х |
|
|
? |
ex + C |
? |
? |
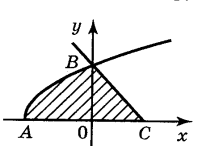
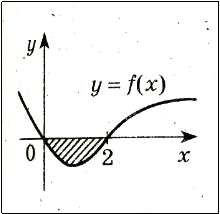
2. Запишіть формулу для обчислення площі фігури, зображеної на рисунку:(2 бали)
3. Обчисліть площу фігури (за допомогою рисунка)(2 бали)
4. Обчисліть (спочатку побудувавши рисунок) площу фігури, обмеженої лініями:
а) у = 1 -х, у = 3 - 2х - х2 (3 бали)
![]() у = х3, у =х. (3 бали)
у = х3, у =х. (3 бали)
Варіант 2.
1. Вставте пропущені вирази:(2 бали)
|
х7 |
|
ex |
|
cos х |
|
?
|
? |
ex + C |
? |
? |
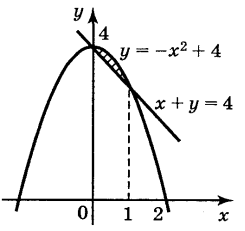
2. Запишіть формулу для обчислення площі фігури, зображеної на рисунку:(2 бали)
3. Обчисліть площу фігури (за допомогою рисунка)
(2 бали)
4. Обчисліть (спочатку побудувавши рисунок) площу фігури, обмеженої лініями:
а) у =x2 + 1, у =x + 3 (3 бали)
б) ![]() ,
,![]() (3 бали)
(3 бали)
Вріант 3.
1. Вставте пропущені вирази: (2 бали)
|
х |
|
cos х |
|
? |
|
?
|
?
|
sinx+ C |
? |
ex + C |
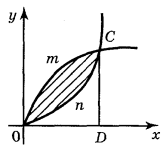
2. Запишіть формулу для обчислення площі фігури, зображеної на рисунку: (2 бали)
3. Обчисліть площу фігури (за допомогою малюнка) (2 бали)
4. Обчисліть (спочатку побудувавши рисунок) площу фігури, обмеженої лініями:
а) у = 4 - х2, у =x + 2, у = 0 (3 бали)
б) у =x2 - 2х + 3, у = 5 – х (3 бали)
Вріант 4.
1. Вставте пропущені вирази: (2 бали)
|
|
? |
? |
|
? |
|
? |
|
ex + C |
tgx+C |
sinx+ C |
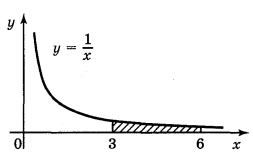
2. Запишіть формулу для обчислення площі фігури, зображеної на рисунку: (2 бали)
3. Обчисліть площу фігури (за допомогою малюнка) (2 бали)
4. Обчисліть (спочатку побудувавши рисунок) площу фігури, обмеженої лініями:
а) у = 3х2, у = 1,5х + 4,5, у =0 (3 бали)
б) у = х3, у = ![]() . (3 бали)
. (3 бали)
Варіант 5.
1. Вставте пропущені вирази:(2 бали)
|
|
|
? |
? |
sin х |
|
? |
? |
|
-ctgx+C? |
-cosx+ C |
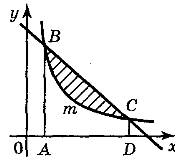
2. Запишіть формулу для обчислення площі фігури, зображеної на рисунку:(2 бали)
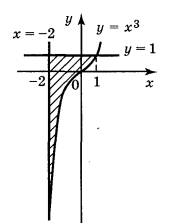
3.Обчисліть площу фігури (за допомогою рисунка)
(2 бали)
4. Обчисліть (спочатку побудувавши рисунок) площу фігури, обмеженої лініями:
а) у =x2 + 1, у = 3-х (3 бали)
б) у = ![]() , у = 2 - х2, х = 1, у = 0 (3 бали)
, у = 2 - х2, х = 1, у = 0 (3 бали)
Варіант 6.
1. Вставте пропущені вирази:(2 бали)
|
|
? |
sin х |
|
? |
|
ln |
|
? |
? |
ex + C |
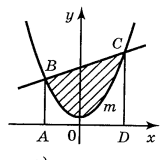
2. Запишіть формулу для обчислення площі фігури, зображеної на рисунку:(2 бали)
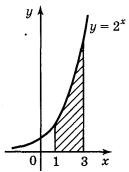
3. Обчисліть площу фігури (за допомогою рисунка)
(2 бали)
4. Обчисліть (спочатку побудувавши рисунок) площу фігури, обмеженої лініями:
а) у = ![]() , у = х (3 бали)
, у = х (3 бали)
б) у = х3, у =2х - х2, у = 0; (3 бали)
![]()
Ключі відповідей.
Варіант 1.
|
2 |
3 |
4а |
4б |
|
S = SABO + SOBC |
|
4,5 |
|
Варіант 2.
|
2 |
3 |
4а |
4б |
|
S=SFBmCD – SFBCD |
|
4,5 |
|
Варіант 3.
|
2 |
3 |
4а |
4б |
|
S =SОmCD– SOnCD |
ln2 |
6 |
4,5 |
Варіант 4.
|
2 |
3 |
4а |
4б |
|
S = SАВСD – SАВED |
ln2 |
4 |
|
Варіант 5.
|
2 |
3 |
4а |
4б |
|
S = SABCD – SABmCD |
6 |
4,5 |
2 |
Варіант 6.
|
2 |
3 |
4а |
4б |
|
S = SABCD– SABmCD |
|
|
|
6. Самостійна робота №5.
Пояснювальна записка.
Самостійна робота № 5 має в своєму складі 6 варіантів одного рівня складності, що дає змогу поставити студентів однієї групи в рівні умови.
В складі кожного варіанта є 7 завдань : перші3 завдання початкового рівня на повторення загального вигляду первісних, обчислення нескладних невизначених та визначених інтегралів,одне завдання на уміння записувати формулу для обчислення площі фігури, всі інші завдання достатнього та високого рівня тому, що потребують вміння обчислювати площі плоских фігур, обмежених графіками функцій за допомогою визначеного інтегралу.
Метою даної роботи є навчання, тренування , закріплення умінь та навичок обчислення площ криволінійних трапецій та фігур.
Орієнтовний час виконання самостійної роботи 30 хвилин.
Варіанти завдань.
Варіант 1.
1. Загальний вигляд первісної для функції ![]() є:(1 бал)
є:(1 бал)
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
2. Знайдіть невизначений![]() (1 бал)
(1 бал)
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
3. Обчисліть інтеграл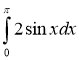 .(1 бал)
.(1 бал)
 а) 1; б) 4; в) 0; г) -2.
а) 1; б) 4; в) 0; г) -2.
4. Обчисліть інтеграл
(2 бали)
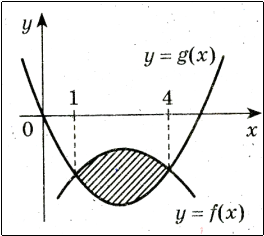
5. Запишіть формулу для обчислення площі фігури, зображеної на рисунку:(2 бали)
6. Обчисліть площу фігури (за допомогою рисунка)
(2 бали)
7. Обчисліть площу фігури, обмеженої лініями:(3 бали)
![]() .
.
Варіант 2.
1. Загальний вигляд первісної для функції![]() є: (1 бал)
є: (1 бал)
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
2. Знайдіть невизначений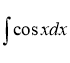 : (1 бал)
: (1 бал)
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
3. Обчисліть інтеграл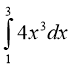 . (1 бал)
. (1 бал)
 а) 80; б) 16; в) 8; г) 15.
а) 80; б) 16; в) 8; г) 15.
4. Обчисліть інтеграл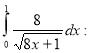 (2 бали)
(2 бали)
5. Запишіть формулу для обчислення площі фігури, зображеної на рисунку:(2 бали)
6.Обчисліть площу фігури (за допомогою рисунка)
(2 бали)
7. Обчисліть площу фігури, обмеженої лініями:(3 бали)
![]() .
.
Варіант 3
1. Загальний вигляд первісних для у = ах: (1 бал)
а) ах +С б) ах в) ![]() +C г) ахlna+C
+C г) ахlna+C![]()
2. Знайдіть невизначений![]() (1 бал)
(1 бал)
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
3.Обчисліть інтеграл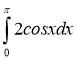 . (1 бал)
. (1 бал)
 а) 1; б) 4; в) 0; г) -2.
а) 1; б) 4; в) 0; г) -2.
4. Обчисліть інтеграл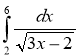 ; (2 бали)
; (2 бали)
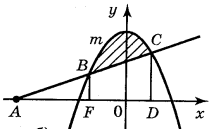
5. Запишіть формулу для обчислення площі фігури, зображеної на рисунку: (2 бали)
 6.Обчисліть площу фігури (за допомогою рисунка)
6.Обчисліть площу фігури (за допомогою рисунка)
(2 бали)
.
7. Обчисліть площу фігури, обмеженої лініями: (3 бали)
![]() .
.
Вріант 4.
Загальний вигляд первісних для у = cosx :![]() (1 бал)
(1 бал)
а) sinx б) cosx+C в) sinx+C г) - sinx+C![]()
2. Знайдіть невизначений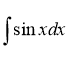 :(1 бал)
:(1 бал)
а) ![]() б) -
б) -![]() в)
в) ![]() г)
г) ![]()
3. Обчисліть інтеграл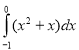 . (1 бал)
. (1 бал)
 а)
а) ![]() ; б) 1; в)
; б) 1; в)![]() ; г) -3.
; г) -3.
4. Обчисліть інтеграл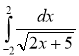 ; (2 бали)
; (2 бали)
5. Запишіть формулу для обчислення площі фігури, зображеної на рисунку: (2 бали)
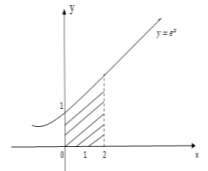
6. Обчисліть площу фігури (за допомогою рисунка) (2 бали)
7. Обчисліть площу фігури, обмеженої лініями: (3 бали)
![]() .
.
Варіант 5.
1. Загальний вигляд первісних для у = е![]() є: (1 бал)
є: (1 бал)
а) е![]() б)
б) ![]() + С в)
+ С в) ![]() + С г) е
+ С г) е![]() + С
+ С
2. Знайдіть невизначений![]() :(1 бал)
:(1 бал)
а) ln![]() +C; б) х + С ; в) е
+C; б) х + С ; в) е![]() + С ; г)
+ С ; г) ![]() + С.
+ С.
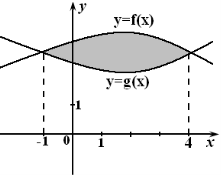
3. Обчисліть інтеграл![]() (1 бал)
(1 бал)
а) 8; б) 4; в) 3; г) 2.
 4. Обчисліть інтеграл
4. Обчисліть інтеграл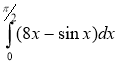 (2 бали)
(2 бали)
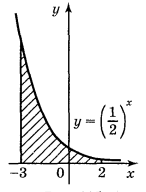
5. Запишіть формулу для обчислення площі фігури, зображеної на рисунку: (2 бали)
6. Обчисліть площу фігури (за допомогою рисунка)
(2 бали)
7. Обчисліть площу фігури, обмеженої лініями: (3 бали)
![]() .
.
Варіант 6.
1. Загальний вигляд первісних для у = ![]() : (1 бал)
: (1 бал)
а) lnx +C б) ![]() + C в) ln
+ C в) ln![]() + С г)
+ С г) ![]() + C
+ C
2. Знайдіть невизначений![]() :(1 бал)
:(1 бал)
а) ln![]() +C; б) х + С ; в) е
+C; б) х + С ; в) е![]() + С ; г)
+ С ; г) ![]() + С.
+ С.
 3. Обчисліть інтеграл
3. Обчисліть інтеграл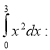 (1 бал)
(1 бал)
а) 9; б) 3; в) 27; г) 6.
4. Обчисліть інтеграл 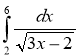 ; (2 бали)
; (2 бали)
5. Запишіть формулу для обчислення площі фігури, зображеної на рисунку: (2 бали)
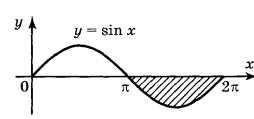 6. Обчисліть площу фігури (за допомогою рисунка)
6. Обчисліть площу фігури (за допомогою рисунка)
(2 бали)
7. Обчисліть площу фігури, обмеженої лініями: (3 бали)
у = х2; у = 2х2 - 1
Ключі відповідей
Варіант 1.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
б |
в |
б |
2 |
|
2 |
21 |
Варіант 2.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
б |
г |
а |
4 |
|
3,75 |
21 |
Варіант 3.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
в
|
в
|
в
|
1
|
|
ln2 |
8 |
Варіант 4.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
в |
б |
|
2
|
|
|
2 |
Варіант 5.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
г |
а |
а
|
|
|
|
|
Варіант 6.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
в |
б |
а |
|
|
2 |
|
7. Самостійна робота №6.
Пояснювальна записка.
Самостійна робота № 6 має в своєму складі 6 варіантів одного рівня складності, що дає змогу поставити студентів однієї групи в рівні умови.
В складі кожного варіанта є всього два завдання на обчислення площі фігур за готовими малюнками, інші завдання достатнього та високого рівня потребують вміння обчислювати площі плоских фігур, обмежених графіками функцій за допомогою визначеного інтегралу.
Метою даної роботи є навчання, тренування , закріплення умінь та навичок обчислення площ криволінійних трапецій та фігур.
Орієнтовний час виконання самостійної роботи 25-30 хвилин.
Варіанти завдань
Варіант 1.
1. Обчисліть площу фігур, зображених на малюнках : ( 6 балів)
а) б) в)
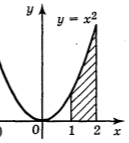
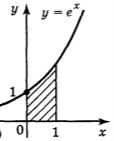
2. Обчисліть площу фігури, обмеженої лініями:
а) y=x2-2x+4, y=x+4 ( 3 бали)
б) y=x2-10x+24, y=2x-8 ( 3 бали)
Варіант 2.
1. Обчисліть площу фігур, зображених на малюнках :( 6 балів)
а) б) в)
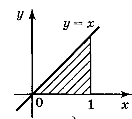
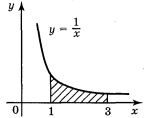
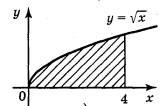
2. Обчисліть площу фігури, обмеженої лініями:
а) y=-x2+10x-20, y=3x-14 ( 3 бали)
б) y=-x2+8x-11, y=2x-11 ( 3 бали)
Варіант 3.
1. Обчисліть площу фігур, зображених на малюнках :( 6 балів)

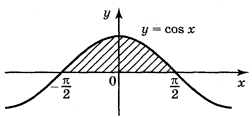
 а) б) в)
а) б) в)
2. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-2x, y=x+4 ( 3 бали)
б) y=x2+6x-4, y=-x-4 ( 3 бали)
Варіант 4.
1. Обчисліть площу фігур, зображених на малюнках :( 6 балів)
а) б) в)
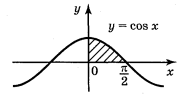
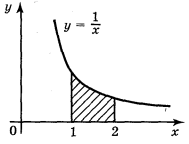
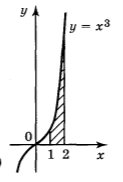
2. Обчисліть площу фігури, обмеженої лініями:
а) y=x2-2x+4, y=x+8 ( 3 бали)
б) y=-x2+8x-13, y=2x-13 ( 3 бали)
Варіант 5.
1. Обчисліть площу фігур, зображених на малюнках :( 6 балів)
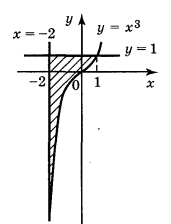
а) б) в)
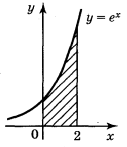
2. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-10x+28, y=2x-4 ( 3 бали)
б) y=x2-2x+2, y=x+2 ( 3 бали)
Варіант 6.
1. Обчисліть площу фігур, зображених на малюнках :( 6 балів)
а) б) в) 
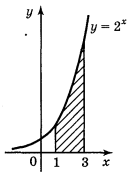

2. 2.
2. Обчисліть площу фігури, обмеженої лініями:
а) y=-x2+10x-22, y=3x-16 ( 3 бали)
б) y=-x2+6x-6, y=-x-6 ( 3 бали)
Ключі відповідей
Варіант 1.
|
1а |
1б |
1в |
2а |
2б |
|
2 |
е-1 |
|
4.5 |
|
Варіант 2.
|
1а |
1б |
1в |
2а |
2б |
|
|
|
ln3 |
|
36 |
Варіант 3.
|
1а |
2б |
1в |
2а |
2б |
|
ln2 |
|
2 |
|
|
Варіант 4.
|
1а |
1б |
1в |
2а |
2б |
|
|
1 |
ln2 |
|
36 |
Варіант 5.
|
1а |
1б |
1в |
2а |
2б |
|
|
|
|
|
4,5 |
Варіант 6.
|
1а |
1б |
1в |
2а |
2б |
|
|
|
2 |
|
|
Індивідуальні завдання за темою «Інтеграл та його застосування»
Пояснювальна записка
Дана збірка індивідуальних завдань для самостійної роботи по темі «Інтеграл та його застосування» має в своєму складі 30 варіантів одного рівня складності, що дає змогу поставити студентів однієї групи в рівні умови.
Але в самому складі кожного варіанта індивідуального завдання є завдання початкового і середнього і високого рівнів на майже всі основі типи вправ і задач і на застосування основних методів і шляхів їх розв’язання.
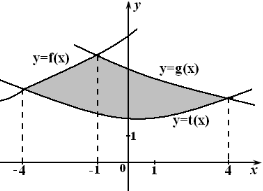
Завдання № 1а, № 1б на знаходження визначеного інтеграла, а також завдання № 2 на знаходження площі криволінійної трапеції – це завдання достатнього рівня складності.
Завдання № 3 а, б– завдання високого рівня, тому що потребують, вміння обчислювати площі плоских фігур, обмежених графіками функцій за допомогою визначеного інтегралу.
При виконанні індивідуального завдання по темі «Інтеграл та його застосування» студент таким чином має можливість закріпити знання і відпрацювати вміння і навички по застосуванню різноманітних форм і методів розв’язування вправ і задач даної теми.
Критерії оцінювання
Кожний варіант індивідуального завдання для самостійної роботи студентів по темі «Інтеграл та його застосування» містить в своєму складі 4 завдання різного рівня складності.
Завдання № 4 на знаходження первісної, графік якої проходить через точку – це завдання середнього рівня складності, яке максимально оцінюється 2 балами.
Завдання № 1а, № 1б на знаходження визначеного інтеграла оцінюються кожне по 1 балу, а завдання достатнього рівня № 2 на знаходження площі криволінійної трапеції – максимально двома балами.
Завдання високого рівня № 3 а, б, які потребують вміння обчислювати площі плоских фігур, обмежених лініями оцінюються максимально по 3 бала кожне.
Таким чином, при правильному розв’язанні студент може отримати:
2∙1+2+2∙3+2=2+2+7+1=12 б.
Варіанти завдань
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 1
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
у =3 x2 +2x, y=0, x=0, x=5
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2+2x+1, y=x+3
б) y=-x2+6x-8, y=-x-8
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=7x6-8x-10 A (-1; 3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 2
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=6 x2 +2x, y=0, x=0, x=4
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-2x+3, y=x+7
б) y=-x2+6x-7, y=-x-7
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=7x6-6x-4 A (-1; 10)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 3
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=9 x2 +2x, y=0, x=0, x=3
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-10x+28, y=2x-4
б) y=-x2+8x-13, y=2x-13
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=7x6-4x-5x4 A (2; 3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 4
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=18 x2 +2x, y=0, x=0, x=2
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-2x+5, y=x+9
б) y=-x2-2x+3, y=x+3
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=7x6-2x-8x2 A (2; 11)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 5
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=12 x2 +2x, y=0, x=0, x=3
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-2x, y=x+4
б) y=x2+6x-4, y=-x-4
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=12x5-14x-16x2 A (1; 3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 6
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=15x2+2x, y=0, x=0, x=2
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-2x-1, y=x+3
б) y=x2-10x+23, y=2x-9
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=12x5-12x3-4 A (-1; 3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 7
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=3 x2 -2x, y=0, x=0, x=5
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-2x+6, y=x+6
б) y=x2-2x-2, y=x+2
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=12x5-15x2-10x A (2; 3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 8
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=6 x2 -2x, y=0, x=0, x=4
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-2x, y=x
б) y=x2-2x-3, y=x+1
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=12x5-8x-6x2 A (2; -1)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 9
- Обчисліть інтеграл:
а)![]() б)
б) 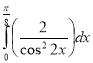
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=9 x2 -2x, y=0, x=0, x=3
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-2x-4, y=x
б) y=x2-10x+20, y=2x-12
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=12x5-6x+10x +4 A (-2; 3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 10
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=12 x2 -2x, y=0, x=0, x=2
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x210x+19, y=2x-13
б) y=x2-2x-2, y=x-2
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=12x5-9![]() -20x4 A (2;- 3)
-20x4 A (2;- 3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 11
- Обчисліть інтеграл:
а)![]() б)
б)![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=15 x2 -2x, y=0, x=0, x=1
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-4x+5, y=x+5
б) y=2x2-12x+17, y=-2x+9
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=12x5-6x2-2x A (2;- 3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 12
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=18 x2 -2x, y=0, x=0, x=1
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-4x+6, y=x+6
б) y=-x2+2x, y=-x-10
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=6x5-7x6+8x A (2; -3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 13
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=3 x2 +44x, y=0, x=0, x=2
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2+4x+7, y=x+7
б) y=x2-8x+17, y=2x-4
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=6x5-12x3-5x4 A (2; -1)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 14
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=6 x2 +4x, y=0, x=0, x=2
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-4x+6, y=x+2
б) y=x2-6x+10, y=x+4
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=6x5-10x4-6 A (2; -4)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 15
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=9x2 +4x, y=0, x=0, x=2
3. Обчисліть площу фігури, обмеженої лініями:
а) y = -x2+2x-11, y=3x-11
б) y=x2-4x+7, y=x+3
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=6x5-15x4+4x A (2;- 3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 16
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=12 x2 +4x, y=0, x=0, x=2
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-6x+12, y=x+6
б) y=x2-8x+20, y=2x-1
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=6x5-16x3-4x A (2; 3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 17
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=3 x2 -4x, y=0, x=0, x=3
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-8x+15, y=2x-6
б) y=x2-4x+9, y=x+5
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=6x5-21x2-2x A (2; -3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 18
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=6x2 -4x, y=0, x=0, x=4
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-6x+14, y=x+8
б) y=2x2-12x+19, y=-2x+11
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=30x4-18x2-6x A (2; -5)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 19
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=39x2 -4x, y=0, x=0, x=1
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-6x+8, y=x+2
б) y=-x2+2x+7, y=-x-3
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=25x4-24x3-6x A (2;- 3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 20
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=9x2 +4x, y=0, x=0, x=2
3. Обчисліть площу фігури, обмеженої лініями:
а) y = -x2+2x-11, y=3x-11
б) y=x2-4x+7, y=x+3
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=7x6-6x-4 A (-1; 10)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 21
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=15 x2 -4x, y=0, x=0, x=2
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-4x, y=x-4
б) y=x2-6x+6, y=x
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=20x4-16x3-12x A (2; -5)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 22
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=18x2 -4x, y=0, x=0, x=1
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-4x-1, y=x-5
б) y=x2-6x+5, y=x-1
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=15x4-27x2-4x A (2; -9)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 23
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=3 x2 +6x, y=0, x=0, x=1
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-6x+4, y=x-2
б) y=x2-8x+9, y=2x-12
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=10x4-24x3-21x2 A (2; -1)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 24
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=3 x2 +8x, y=0, x=0, x=2
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-6x+10, y=2x-2
б) y=x2-4x+10, y=x
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=10x4-16x3-15x2 A (2; -3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 25
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=6 x2 -6x, y=0, x=0, x=3
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-4x+3, y=x+3
б) y=2x2-4x+1, y=-2x+10
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=5x4-8x-10x-6x2 A (2; 10)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 26
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=6 x2 -8x, y=0, x=0, x=2
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-4x+2, y=x+2
б) y=-x2+4x+1, y=-x-5
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=28x3-6x2-10x A (2; -3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 27
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=9 x2 -6x, y=0, x=0, x=3
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-4x+1, y=x+1
б) y=x2-6x+13, y=2x+1
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=24x3-10x-4x A (2;- 3)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 28
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=9 x2 -8x, y=0, x=0, x=2
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-6x+7, y=x-3
б) y=x2-4x+2, y=x
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=20x3+2x-7x6 A (2; -5)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 29
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=12 x2 -6x, y=0, x=0, x=3
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-6x+6, y=x-4
б) y=x2-4x-1, y=x-1
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=35x4-4x3-18x A (2; -9)
Індивідуальне завдання «Інтеграл та його застосування»
з дисципліни «Математика»
Варіант № 30
- Обчисліть інтеграл:
а)![]() б)
б) ![]()
2. Обчисліть площу криволінійної трапеції, обмеженої лініями:
y=12 x2 -8x, y=0, x=0, x=3
3. Обчисліть площу фігури, обмеженої лініями:
а) y = x2-4+1, y=x-2
б) y=-x2+4x+5, y=-x-1
4. Для заданої функції y(x) знайдіть первісну, графік якої проходить
через задану т. А:
y=7x6-12x3-4x A (2; -8)
Висновки
Самостійну роботу студентів в залежності від свого призначення можна розбити на декілька видів: навчаючі, тренувальні, закріплюючі, повторюючи, розвиваючі, контрольні.
Я працювала над розробкою різноманітних видів самостійної роботи за темою «Площа криволінійної трапеції. Площа фігури» із розділу «Інтеграл та його застосування». Були застосовані тестові завдання з одиночним вибором та на встановлення відповідності, завдання на заповнення таблиці відповідності функції та її первісної. Завдання на обчислення площ криволінійних трапеції та площ фігур різноманітні, від простих, в яких вже є малюнок, до більш складних, що потребують глибоких знань ,умінь і навичок в побудові графіків функцій, обчисленні границь інтегрування, застосуванні формули Ньютона – Лейбніца і т.д.
Завдання для самостійної роботи супроводжуються пояснювальними записками, критеріями оцінювання та ключами відповідей.
При складанні завдань для самостійної роботи перш за все я намагалась враховувати, що степінь складності завдань повинен відповідати учбовим можливостям студентів.
Я вважаю, що дана методична розробка може бути корисна для викладачів математики навчальних закладів І-ІІ рівня акредитації та загальноосвітніх шкіл.
Бібліографія
- Бевз Г.П. Алгебра і початки аналізу (підручник для шкіл, ліцеїв, гімназій гуманітарного напряму), 10-11 кл. – К.: ТОВ «Бліц», 2005
- Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу (підручник) , 10-11 кл. – К.: Зодіак – ЕКО, 2002.
- Афанасьєва О.М. , Бродський Я.С. та інш. Дидактичні матеріали з математики: Навч. Посібник,-К., „Вища школа”, 2001р.
- Яковлев Г.Н. Математика для техникумов І ч.Алгебра и начала анализа. Учебник.-М.:Наука 1987.
- Роєва Т. Г., Хроленко Н. Ф. Алгебра та початки аналізу у таблицях за новою програмою 10-11 клас: Навч. Посібник.- Х,: Країна мрій,2002
- Богданова Л.Г., Кінащук Н.Л. Зовнішнє оцінювання. Математика. 11 кл. X.: Гімназія, 2007
- Бродський Я.С., Павлов О.Л. Математика. Тести для самостійної роботи та контролю знань, 10-11 кл. - Тернопіль: Навчальна книга - Богдан, 2003
- Захарійченко О.В., Школьний Ю.В. Тестові завдання з математики. - К.: Генеза, 2007
- Прокопенко Н.С., Мерзляк А.Г., Полонський В.Б., Якір М.С. Математика. Збірник завдань для тематичного оцінювання знань, 10,11 кл. - К.: КІМО, 2001
- Роєва Т.Г., Адруг Л.М. Алгебра і початки аналізу. Завдання для тематичного оцінювання^ 10, 11 кл. - К.: Країна мрій, 2007
Додаток 1


про публікацію авторської розробки
Додати розробку