Навчально-методичний збірник на допомогу вчителям "Формування компетентності через розвиток творчих здібностей учнів"

 

 

 

 

 

 

 

 

 

Іваницька Арета Михайлівна

Пелих Яромира Володимирівна

 

 

 

 

 

Навчально-методичний збірник

на допомогу вчителям

 

Формування компетентності

через розвиток творчих

здібностей учнів

 

 

 

 

 

 

 

 

 

 

 

Зміст   

Вступ...................................................................................................... 4

Розділ 1. Формування ключових компетентностей учнів……... 6

1.1. Ключові компетентності в українській школі…………...…7

1.2. Ключові компетентності випускника школи……..………..8

1.3. Навчальні досягнення учнів  за компетентнісним                 підходом………………………………………………………9

1.4. Взаємозв'язок ключових і предметних компетнтностей…..9

Розділ 2. Розвиток творчих здібностей учнів................................10

2.1. Основні компоненти формування творчих здібностей у підлітків...................................................................................11

Розділ3. Факультативне навчання математики..........................13

3.1. Методи навчання на факультативних заняттях…………..15

3.2. Матеріали на допомогу вчителю в підготовці                    факультативних занять з математики……………………..16

Розділ 4. Математичні гуртки……………………………..………25

4.1. Матеріали на допомогу вчителю в підготовці                      математичних гуртків…………………………….………...27

Розділ 5. Позакласна робота з математики. Характеристика   напрямків   позакласної роботи з математики……...…42

Висновки. ............................................................................................48

Бібліографія.........................................................................................49

 

 

 

 

 

 

Вступ

Реалізуючи основну мету курсу математики в середній школі, необхідно водночас створювати умови для розвитку кожної особистостіз урахуванням її нахилів та природних обдарувань. Застосування варіативного компоненту навчального плану загальноосвітньої школи відкриває для цього достатньо можливостей. Розширення кола факультативівта курсів за вибором дозволяє ознайомити учнів із деякими загальнимиматематичними ідеями, показати застосування математики у практичнійдіяльності.

Методологічною основою розвитку інноваційної особистості школяра є  створення креативної системи освіти на основі компетентнісного підхіду до навчання та виховання, тобто розвиток його ключових компетентностей, оволодіння якими допоможе учневі критично мислити, здобувати й аналізувати інформацію, розв’язувати конфлікти, дозволить вирішити різні проблеми в професійному, соціальному, повсякденному житті та багато іншого, що забезпечує людині гармонійну взаємодію з високотехнологізованим суспільством, яке, до того ж, швидко розвивається.

На жаль, поняття компетентності у психолого-педагогічній літературі визначено неоднозначно і в багатьох випадках вживається на інтуїтивному рівні. Питання компетентності особистості висвітлювали такі вчені, як В.О. Кальней, В.Ландшеєр, Дж. Равен, С.Є. Шишов, М.А. Чошанов та інші.

Міжнародним департаментом стандартів для навчання та освіти поняття компетентності визначається як спроможність кваліфіковано здійснювати діяльність, виконувати завдання або роботу. При цьому поняття компетентність містить набір знань, навичок та відношень, що дають змогу особистості ефективно здійснювати діяльність або виконувати певні функції, що сприяють досягненню певних стандартів у галузі професії або виді діяльності.

В умовах реформування системи освіти, відтворення і зміцнення інтелектуального потенціалу нації, виходу вітчизняної науки і техніки, економіки і виробництва на світовий рівень, інтеграції в світову систему освіти, переходу до ринкових відносин і конкуренції будь-якої продукції, в тому числі й інтелектуальної, особливо актуальним стає забезпечення належного рівня математичної підготовки підростаючого покоління.

Математика має широкі можливості для інтелектуального розвитку особистості, в першу чергу, розвитку логічного мислення, просторових уявлень  і  уяви,  алгоритмічної  культури,  формування  вміння встановлювати причинно-наслідкові зв'язки, обґрунтовувати твердження, моделювати ситуації та ін. Математика є засобом вивчення фізики, хімії, інформатики   та   обчислювальної  техніки,   астрономії,   біології, загально технічних і спеціальних дисциплін, мовою техніки, а розвинене логічне мислення сприяє засвоєнню гуманітарних предметів. Математичне моделювання широко використовується для розв'язування задач різних галузей науки, економіки, виробництва. Практичні вміння і навички з математики необхідні для майбутньої трудової діяльності школярів.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розділ 1.

Формування ключових компетентностей учнів

 

Від нас, від нашого вміння,від нашої майстерності,від нашого мистецтва та мудрості залежить життя,здоров’я, розум, характер,воля, інтелектуальне обличчя,місце та роль у житті,щастя підростаючого покоління.

В.О. Сухомлинський

 

Компетентність походить від латинського competens (competentic), що в перекладі означаєколо питань, у яких людина добре обізнана, має знання та досвід. Людина, компетентна в певній сфері діяльності, має відповідні знання та здібності, що дозволяють їй ефективно діяти в цій сфері, авторитетно судити про те, що в ній відбувається..

Компетентність – інтегрована здатність особистості, яка набута у процесі навчання і дозволяє їй судити про що-небудь, висловлювати авторитетну, переконливу думку. Вона охоплює:  знання, уміння, навички, досвід, цінності та ставлення, які можуть цілісно реалізуватися на практиці, тому компетентність не може бути зведена лише до фактичних знань.

Компетентний – значить знаючий, обізнаний у певній галузі; що має право за своїми знаннями і повноваженнями робити або вирішувати що-небудь, судити про щось.

До ключових компетентностей учнів, формування яких покладається на школу, належать: пізнавальні компетентності, особистісні компетентності, самоосвітні компетентності, соціальні компетентності, здоров’я особистості, творчі компетентності.

Радою Європи запропоновано формувати в учнів середньої школи сім груп ключових компетентностей:

• грамотність (читання, письмо, арифметика)
• загальні навички (комунікація, уміння навчатися, лідерство);
• особистісні компетентності (вмотивованість, цікавість, креативність, чесність, наполегливість тощо);
• інформаційно-комунікаційні компетентності;
• володіння іноземними мовами;
• компетентності з науки і технологій, які передбачають володіння науковою грамотністю;
• соціальні компетентності як інструмент підтримання стосунків для економічної і соціальної інтеграції в багатонаціональному та багатокультурному суспільстві;

1.1. Ключові компетентності в українській школі

• уміння вчитися (навчальна);
• громадянська;
• загальнокультурна;
• компетентність з інформаційних  та комунікаційних технологій;
• соціальна;
• підприємницька;
• здоров’язбережувальна.

Для того, щоб навчати дітей творчості у вирішенні різних пізнавальних завдань,і в перспективі – до уміння вибудувати успішне життя, вчителю теж треба змінювати свій підхід до навчання.

Вирішенню питання формування творчих компетентностей учнів сприяє застосування інноваційних технологій навчання, до яких належать такі найбільш поширені: особистісно орієнтоване навчання та виховання, рівнева диференціація навчання, проектне навчання, проблемне навчання, інтерактивні технології, технологія формування творчої особистості, технологія навчання як дослідження, технологія гуманізації педагогічної діяльності, розвиток критичного мислення, теорія ігрових технологій та ін..

Одним з кращих прикладів формування та розвитку життєвих компетентностей учнів є проектна методика яка сприяє розвитку ініціативи самостійності організаторських здібностей, стимулює процес саморозвитку, самореалізації учнів. Під час використання проектної технології формуютьсякомпетентності яких потребує життя.

•            Соціальні:навички роботи в групі
•            Інформаційні:уміння самостійно здобувати інформацію
•            Комунікативні:вдосконалення спілкування в групі
•            Компетентності саморозвитку та самоосвіти

 

1.2. Ключові компетентності випускника школи

Пізнавальна компетентність:

•            навчальні досягнення;
•            інтелектуальні знання;
•            уміння навчатися та оперувати знаннями.

Особистісна компетентність:

•            розвиток індивідуальних здібностей і талантів;
•            обізнаність у власних сильних і слабких сторонах;
•            здатність до рефлексії;
•            динамічні знання.

Самоосвітня компетентність:

• здатність до самонавчання, розробка власних прийомів самоосвіти;
•  відповідальність за рівень власної самоосвітньої діяльності;
•  гнучкість застосування знань, умінь, навичок в умовах швидких змін;
• постійний самоаналіз, самоконтроль за власною діяльністю.

Соціальна компетентність:

• вміння співпрацювати, робота в команді, комунікативні навички;
• здатність приймати свої рішення і прагнення до розуміння власних потреб;
• соціальне єднання, вміння визначити особисті ролі в суспільстві;
• ціннісні орієнтації;
• розвиток особистісних якостей, саморегуляція;
• культура міжособистісних відносин.

Здоров’я особистості:

•            соматичне здоров’я;
•            клінічне здоров’я;
•            фізичне здоров’я;
•            психічне здоров’я;
•            рівень валеологічних знань.

 

 

 

 

 

1.3. Навчальні досягнення учнів  за компетентнісним підходом

 

Знання	Я знаю (уявлення, факти, відомості, ознаки, поняття)
Діяльність	Я знаю, як це зробити… я вмію…, я можу… я роблю…
Творчість	Я створюю, я придумую… я змінюю… я знаходжу… я доповнюю…
Ставлення	Я прагну до… я хочу досягти… я ціную… я схвалюю… я заперечую… я думаю інакше…

 

1.4. Взаємозв'язок ключових і предметних компетнтностей

 

 

 

 

 

 

 

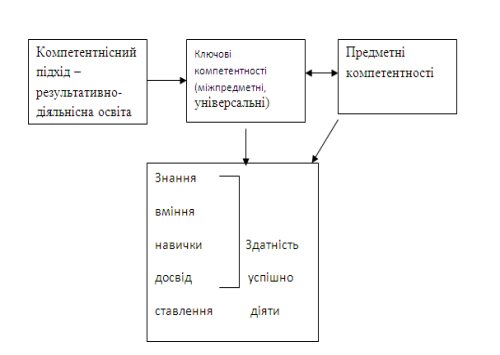
Розділ 2

Розвиток творчих здібностей учнів

" Якщо твої плани розраховані на рік ­­– сій хліб, якщо на десятиріччя – посади дерево,

якщо на віки – навчай дітей"

Давня мудрість

 

Школа є тією лабораторією, де навчають і виховують, відкривають можливості кожної дитини, допомагають їй розвивати власні здібності й потреби. Кожна дитина по-своєму неповторна. Вона приходить уцей світ, щоб творити своє життя, самореалізуватися: хтось здібний до музики, образотворчого мистецтва, художньої праці, хтось до математики, хтось пише вірші, оповідання. Скільки дітей - стільки й здібностей, які залежать від психолого-педагогічних особливостей людини, соціального оточення, сімї та школи.

Творчість - важливий компонент розвитку здібностей дитини. Це розумова й практична діяльність, результатом якої є створення оригінальних, неповторних цінностей, виявлення нових фактів, властивостей, закономірностей, а також методів дослідження і перетворення матеріального світу або духовної культури.

Пояснюючи свою позицію з питань творчості, відомий психолог Л. Виготський зазначив, що "Творчою ми називаємо таку діяльність, яка створює щось нове, однаково, чи буде це створене діяльність будь-якою річчю зовнішнього світі або побудовою розуму або почуття, яке живе та виявляється тільки в самій людині."

Творчі здібності особистості - це синтез її властивостей і рис характеру, які характеризують сутність їх відповідності вимог певного виду навчально-творчої діяльності і які обумовлюють рівень результативності цієї діяльності. Творчі здібності самі по собі не гарантують творчих здобутків. Для їх досягнення необхідний "двигун", який запустив би в роботу механізм мислення, тобто необхідні бажання і воля, потрібна "мотиваційна основа".

Розвиток творчих здібностей у підлітковому віці визначається взаємодією низки чинників:

• внутрішніх, до яких належать: вікові й індивідуально-психологічні особливості особистості (самооцінка, рівень тривожності, агресивність, спрямованість особистості, акцентуація характеру, властивості ВНД, тощо), статеві відмінності, стилі (стратегії) організації розумової діяльності;
• зовнішніх, що представлені чинниками мікросередовища: характером і системою сімейного виховання, впливом школи і спілкування з однорлітками.

Досвід багатьох вітчизняних та закордонних педагогів свідчить про вірогідність успішного формування в учнів якостей творчої особистості. Для цього учням варто надавати максимум можливостей для випробування себе в творчості, причому починати треба з найпростіших завдань.

Навчання творчості має відбуватися в першу чергу і в основному на програмному навчальному матеріалі, а в разі потреби й на спеіцально побудованій системі завдань. Засвоюючи досвід творчої діяльності, характерні для неї процедури, учні набувають здібності видозмінювати ті стереотипи мислення, яким вони вже навчилися, вчаться відмовлятися від стереотипів, конструювати нові підходи до обдумання раніше засвоєного або нового змісту.

2.1. Основні компоненти формування творчих здібностей у підлітків

1.                     Інтелектуально-логічні здібності
2.                     Інтелектуально-еврестичні здібності
3.                     Здібності до фантазії

Інтелектуально-логічні здібності учня виявляють у:

• Вмінні аналізувати (правильність, повнота, глибина).
• Здібності виділяти істотне спільне і відволікатися від несуттєвого (абстрагування, логічність, правильність, глибина суджень і висновків, вміння описувати явища, процеси, логічно звязано, повно і правильно викладати думки).
• Здібності формулювати правильне означення обєкта, встановлювати родову ознаку і видову відміну (стислість, правильність сформульованого означення).

Інтелектуально-еврестичні здібності особистості включають:

• Здібності генерувати ідеї, висувати гіпотези, що характеризує інтелектуально-еврестичні властивості особистості в умовах обмеженої інформації
• Здібності прогнозувати розвязання творчих задач, інтелектуально вбачати і висувати оригінальні підходи, стратегії, методи їх розвязання. (кількість ідейгіпотез, що висуваються особистістю за одиницю часу, їх оригінальність, новизна, ефективність для розвязання творчої задачі).

Здібності до фантазії - це найбільш яскраве виявлення творчої уяви, створення інколи неправдоподібних, парадоксальних образів і понять. критерієм оцінки є яскравість і оригінальність образів, новизна, значушчість фантазії, виявляється при розвязуванні творчих задач.

Критичність мислення - здібність правильно оцінити процес і результат власної творчої діяльності та діяльності інших, уміння знаходити власні помилки, їх причини і причини невдач. Криитерієм оцінки є обєктивність суджень, а також ефективність виявлення причин своїх помилок і невдач.

Сисетма творчих завдань повинна бути орієнтована на формування знань і умінь учнів, одночасно розглядатися і як сукупність творчих завдань, і як єдине ціле. Системоутворюючим фактором обєднання творчих завдань виступає мета сучасної школи, повязана із творчою спрямованістю освіти.

Творчі здібності вчені аналізують як психологічні особливості дитини, які сприяють оволодінню цією діяльністю. Важливо визначитися, які вміння потрібно сформувати в дітей, щоб вони відчували свободу своїх дій у творчості, мали можливість проявити творчість, успішно здійснювати цю діяльність. Природа щедро наділила кожну здорову дитину можливостями розвивати, і потрібно лише знайти, як реалізувати ці можливості, і тоді кожен здоровий малюк зможе піднятися на найбільші висоти творчої діяльності.

Творчість - доля всіх в тому чи іншому ступені, вона ж є норамвльним та постійним супутником дитячого розвитку.

 

 

 

 

 

 

 

 

 

Розділ3

Факультативне навчання математики

Факультативне навчання математики має на меті поглиблювати знання учнів, здобуті при вивченні основного курсу, а також розвивати їх логічне мислення, допитливість і кмітливість.

Його основна мета полягає в тому, щоб, враховуючи інтереси і нахили учнів, розширити і поглибити вивчення програмного матеріалу; ознайомити учнів з деякими загальними математичними ідеями і методами; розвивати математичні здібності учнів прищеплювати учням зацікавленість та смак до самостійних занять з математики; виховувати і розвивати ініціативу та творчість, показати застосування математики на практиці.

У педагогічній науці досить ґрунтовно розкрито істотні ознаки факультативів, що відрізняють їх від звичайних занять: нові форми спілкування учителя й учнів; високий мотиваційний рівень формування юної особистості; необов'язковість оцінювання знань; робота з групами учнів, які мають непогану підготовку і цікавляться математикою.

Часто факультативні заняття проводять за таким планом:

1. Знайомство з матеріалом (доповідає вчитель чи хтось з учнів). 
2. Самостійна робота учнів із завданнями теоретичного та практичного характеру (завдання даються всім однакові).
3. Колективне обговорення розв'язків задач, порівняння способів розв'язків, узагальнення пошуку нових шляхів, перенесення засвоєних прийомів та.методів на інший учбовий матеріал програмного чи факультативного курсу з математики або суміжних предметів.
4. Розв'язування задач підвищеної складності.

Активізують роботу факультативів учнівські конференції, конкурси по розв'язуванню задач "Хто більше...", а в молодших та середніх класах конкурси на самостійне складання кращої задачі за якоюсь темою. Цікавляться учні і колективним обговоренням розв'язків олімпіадних задач.

В залежності від можливостей учнів, їх інтересів та потреб, а також вікових особливостей  факультативні курси різняться за характером та змістом.

Так у VІІ-ІХ кл. доцільно вивчати окремі розділи з математики, не пов'язані між собою, а також питання цікавого характеру, не

обов'язково пов'язані з основним курсом.

Тому для цих класів програми факультативів пропонують такі розділи: "Історія математики", "Математична мозаїка" або програма "Поглиблення основного курсу".

У Х-ХІ кл. поглиблення основного курсу носить систематичний характер і виконує функції підготовки до продовження освіти. Тому програма спрямована на підготовку учнів до іспитів у вузах.

При цьому вчителю дозволено працювати за будь-якою з указаних програм, змінювати зміст факультативних занять, міняти порядок вивчення тем або скласти програму самостійно, але треба пам'ятати, що зміст факультативу повинен поглиблювати та доповнювати основний курс.

І, як на звичайних уроках, на факультативних заняттях треба не лише дбати про знання і навички учнів, а й про виховання наукового світогляду, культури поведінки, мислення, та культури спілкування.

Факультативи допомагають розв’язувати завдання удосконалення змісту і методів навчання. Ці заняття сприяють професійній орієнтації учнів у галузі математики та її застосувань, полегшуючи тим самим вибір спеціальності і подальше удосконалення в ній.

Різниця в діяльності факультативних груп і математичних класів повязана з тим, що факультативи не вимагають перебудови системи навчання математики. Вони працюють на базі загального курсу математики.

Факультативні заняття проводяться 1-2 рази щотижня. В групи для цих занять об'єднують учнів паралельних класів. Заняття проводяться згідно з програмами і навчальними посібниками,запропонованими Міністерством освіти і науки України або програмами, складеним вчителем, які пройшли відповідне затвердження.

Не можна механічно переносити методи, прийоми, організаційні форми і засоби навчання математики в звичайних класах на факультативне навчання. Враховуючи, що учні на факультативних заняттях мають більші можливості у просуванні в навчанні і стійку цікавість до математики, тут мають переважати методи проблемного навчання (проблемний виклад, евристичні бесіди, дослідницький метод). Більше часу потрібно присвятити самостійній роботі. Окремі вчителі ділять виконання завдання дослідницького характеру на кілька етапів. Спочатку учні вивчають потрібну літературу, а потім шукають алгоритм розвязування задачі або проблеми. На заняттях учні звітують про результати своїх пошуків.

Ефективною є лекційно-практична система навчання, в якій належне місце відводиться семінарам. На семінарах учні роблять повідомлення про цікаві застосування математичних методів, способи розвязування нестандартних задач, наводять історичні довідки тощо.

3.1. Методи навчання на факультативних заняттях

При виборі методів і прийомів навчання на факультативних заняттях необхідно врахувати зміст факультативного курсу, рівень розвитку і підготовленості учнів, їх інтерес до тих чи інших розділів програми. Одна з найголовніших вимог до методів полягає в активізації мислення учнів, розвитку самостійності в різних формах її прояву.

Частину матеріалу можна викласти лекційно, особливо при його синтезі і узагальненні. Мета вчителя – показати, як здійснювати подібну організацію матеріалу: деякі подробиці доведень можна опустити, із означень навести тільки найголовніші, але конкретні методи розв'язування задач викласти в такому вигляді, щоб можна було чітко простежити хід розв'язання. Такі лекції корисно проводити з матеріалу, в якому приділяється велика увага відпрацюванню навичок.

Інший тип лекцій використовується, коли метою є не систематизація навичок, а загальний розвиток школярів, наприклад у відношенні розуміння прикладного значення математики. Тут важливо виділити не методи розв'язування окремих типів задач, а ідеї, які є основою для них, або ж самі методи, але в узагальненій формі. У таких лекціях велике місце займають історія, приклади з сучасного життя і виробництва.

Під час проведення лекції можливі бесіди з учнями, постановка задач,  обговорення питань, які виникають у процесі розповіді.

Корисна форма роботи – підготовка учнями рефератів. Виконання таких завдань важливо перш за все у відношенні розвитку навичок самоосвіти, задоволення індивідуальних інтересів учнів. Одночасно індивідуальне завдання повинно мати цінність для всіх учасників факультативної групи. Слід прагнути до того, що підготовлені доповіді заслуховувалися і обговорювалися. До підготовки доповіді можна залучати декількох учнів, які завчасно її вивчили. Вони можуть виконувати роль асистента або опонента доповідача.

Факультативні заняття повинні бути цікавими, захоплюючими для школярів. Добре відомо, що цікавий виклад допомагає розкрити зміст складних наукових понять і проблем. Цікавість допоможе школярам освоїти факультативний курс, ідеї і методи математичної науки, які містяться в ньому, логіку і прийоми творчої діяльності. У цьому відношенні мета вчителя – домогтися розуміння учнями того, що вони підготовлені до роботи над складними проблемами, однак для цього необхідні зацікавленість предметом, працьовитість, оволодіння навичками організації своєї роботи.

3.2. Матеріали на допомогу вчителю в підготовці факультативних занять з математики

При розв'язуванні кожної задачі необхідно вчити учнів думати: узагальнювати, аналізувати, розглядати різні варіанти, складати свої задачі – не тільки аналогічні даним, але ті,які випливають із правил, формул, теорем, властивостей, розглянутих функцій... Набагато корисніше розглядати декілька способів розв'язування однієї (не найпростішої) задачі, ніж швидко розв'язати три чи чотири подібних.

Необхідно систематично озброювати учнів методами проведення доведень (або розв'язування задач на доведення). Доведення від "супротивного", шляхом перебору варіантів і т.д. є великим засобом активізації пізнавальної діяльності не тільки учня, а й дорослого і можуть використовуватися не тільки при навчанні. Для розвитку творчих здібностей учнівможна виділити такі основні  напрями:

1. Лекції, метою яких  є вивчення теми цілим блоком, економлячи час для подальшої творчої роботи.
2. Розв'язування задач, на яких реалізується вивчена теорія.
3. Консультації, на яких питання задають учні, а вчитель відповідає на них.
4. Заліки, метою яких є організація індивідуальної роботи, поступова підготовка до розв'язання складніших задач.

Навчання математиці – це перш за все вміння розв'язувати задачі. Не потрібно розв'язувати багато задач. Багато з них повторюють одна одну, відрізняючись лише числовими значеннями, чи змістом, позначенням або іншими не суттєвими деталями, тоді як їх математична суть однакова. Відомий французьким математик Анрі Пуанкаре (1854-1912) стверджував, що "математика – це мистецтво називати різні речі одним іменем", наприклад, розглянемо три "різні" задачі, математична суть і розв'язування яких одинакові.

1. Майстер може виконати деяку роботу за 20 днів, а учень – за 30 днів. За скільки днів вони виконають цю роботу працюючи разом?
2. Кран з холодною водою наповнює порожній бак за 20 хв., а кран з гарячою – за 30 хв. За який час наповнять порожній бак обидва крани, якщо їх відкрити одночасно?
3. З пункту А в пункт В вирушив потяг, який проходить весь шлях за 20 хв. Одночасно з пункту В в пункт А рухається інший потяг, який проходить цей шлях за 30 хв. Через який час вони зустрінуться?

Розв'язується кожна із цих задач однаково.

1.                     1/20 + 1/30 = 1/12
2.                     1:1/12 = 12

Доцільно перейти до розв'язування нестандартних задач.

1. Який із двох дробів більший

2. Навколо трикутника описано коло. На колі позначені середини дуг, що є вершинами цього трикутника. Після цього трикутник витерли, а коло і середини дуг залишили. Відновити трикутник.
3. В місті п будинків, сума віків яких Т. Від чого місто більше  помолодшає: від того, що знесуть старий будинок, чи від того, що побудують новий? Терміном будівництва або розвалу будинку нехтувати.

Нехай a,b,c..., l можливі прості дільники натурального числа N, причому в розкладі числа N на прості множники число а входить р разів, число b –q разів, ..., а число l –r разів. Знайти кількість можливих дільників N.

4. В трикутнику АВС знайти точку О, для якої добуток довжин перпендикулярів, опущених з точки О на сторони трикутника, набуває найбільшого значення.

5. Як із  квадрата отримати розгортку тетраедра, зробивши тільки один прямолінійний розріз?

Ці задачі сприяють розвитку логічного мислення учнів і ви-

робляють вміння знаходити незвичайні методи розв'язування.

6. Показати, що існують такі ірраціональні числа А і В, що число – А^В раціональне.

Спрощення виразів, які містять радикали

Розглянемо кілька вправ, при розв'язуванні яких можна використати теорему Вієта (пряму і обернену), які дають можливість активізувати знання, пов'язані із властивостями коренів квадратного рівняння.

1. Довести, що

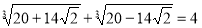
Розв'язання:

Доданки в лівій частині рівняння позначимо nim. Легко порахувати, що nm. Таким чином, якщо рівність правильна, то за теоремою, оберненою до теореми Вієтаnim мають бути коренями квадратного рівняння х² - 4х + 2 = 0, тобто , . Тепер неважко (але обов'язково!) переконатися в тому, що обидві рівності правильні. Потім, додавши їх почленно, отримаємо потрібна твердження.

В наступній задачі поруч з методом, який використаний в задачі 1, пропонується попереднім прикиданням встановити можливий результат. При виконанні вправ, вміння використовувати наближені обчислення, є особливо цінні, так як вони характерні для інженерного, прикладного мислення.

2. Спростити вираз

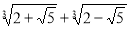
Розв'язання

Обчислимо  наближене значення цього виразу. Воно дорівнює 1. Міркуючи так, як в попередньому завданні, доведемо, що значення цього виразу дорівнює 1. Для цього позначимо , а легко помітити, що nm = -1. Тоді за теоремою, оберненою до теореми Вієта, n і m є коренями рівняння х²-х-1=0. Звідси, і . Перевіримо ці рівності. Піднесемо обидві їх частини до кубу. Додавши ці рівності почленно, отримаємо 1. Отже, наше припущення правильне.

Ці завдання можна розв'язати і іншими способами, наприклад, поданням підкореневих виразів у вигляді куба двочлена.

3. Довести, що .

Розв'язання:

Попробуємо подати число 5√2 + 7, як куб деякої квадратної ірраціональності. 5√2 + 7 = 2√2 + 3√2 + 7 = (√2)³ + 3√2 + 3 (√2)² + 1 =(1 + √2)³. Звідси . АналогічноВіднявши почленно ці дві рівності, отримаємо шукане твердження.

Спрощення виразів, які містять радикали, суттєво полегшують розв'язування рівнянь. Причому такі спрощення інколи можна проводити за допомогою підбору. При розв'язуванні рівнянь цей метод є повністю законним, якщо після отримання коренів ми строго доведемо, що інших коренів нема.

4. Розв'язати рівняння.

Припустимо, що множники, які містять радикали, рівні. Якщо це так, то отримаємо систему 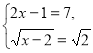. Розв'язавши її, отримаємо х = 4. Легко перевірити, що число 4 є коренем даного рівняння. Тепер покажемо, що інших коренів дане рівняння не має.

Дійсно, при х>4 справедлива система нерівностей 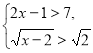. Тоді . Якщо 2≤х<4, то справедлива система нерівностей 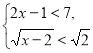тобто . Отже, дане рівняння має єдиний корінь х = 4.

Таким чином, нестроге припущення помагає швидко отримати точну відповідь. Цей підхід розвиває інтуїцію учнів, сприяє до пошуку нестандартних розв'язувань.

5. Розв'язати рівняння .

Розв'язання

Попередній метод в даному випадку не підходить, оскільки система

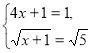не має розв'язку. Попробуємо використати ту ж ідею, але з деякими модифікаціями. Запишемо дане рівняння у вигляді і позначимо 4 х через t. Отримаємо . Припустимо, що множники, які містять радикали, рівні. Тоді рівні і інші множники, тобто, 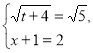. Звідси    t = 1, x = 0,25. Покажемо, що рівняння не має інших коренів. При              х > 0,25  t> 1, тоді . При -1 ≤ х < 0,25 t< 1, тоді . Зауважимо, що при піднесенні обох частин рівняння до квадрату, ми отримаємо рівняння, розв'язання якого виходить за рамки шкільної програми.

Методи розв'язування деяких систем рівнянь

В шкільному курсі "Алгебри і початків аналізу" системи рівняньрозв'язуються тільки способом підстановки чи додавання. Але при розв'язуванні багатьох систем рівнянь можна використовувати і інші способи. Розглянемо один  із них на прикладі трьох завдань.

1. Розв'язати систему рівнянь .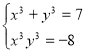

Розв'язання

З умови видно, що х³ у³ є коренями деякого зведеного квадратного рівняння відносно змінної р, р² - 7р - 8 = 0. За теоремою Вієта, коренями цього рівняння є р = 8 і р = - 1. Звідси, х³ = 8, у³ = - 1, або х³ = -1, у³ = 8. Розв'язком даної системи є (2; - 1), (- 1; 2).

2. Розв'язати систему рівнянь .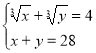

Розв'язання

Обидві частини рівняння піднесемо до куба і після перетворень отримаємо:

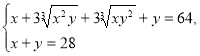
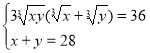
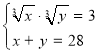
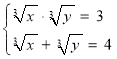
Дальше розв'язуємо аналогічно до розв'язання попереднього завдання. Відповідь (1;27),(27;1).

3. Розв'язати систему рівнянь 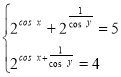.Дану систему запишемо інакше. Відносно змінної zотримаємо рівняння z² -5z + 4 = 0, корені якого 4 або 1. Звідси 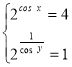або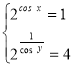. Перша система немає розв'язку, а розв'язок другої є розв'язком даної системи.

Відповідь: , де k, l € Z.

Текстові задачі з практичним змістом

Розв'язання цих задач зводяться до кубічних рівнянь і до знаходження екстремумів функцій двох або трьох аргументів, які розв'язуються без застосування загального способу шукання екстремуму функції n-аргументів.

Розглянемо дві задачі, які зводяться до розв'язування кубічного рівняння.

1. У вертикально поставлену посудину, яка є у формі правильної чотирикутної призми, площа основи якої 4 дм² , налили води до рівня 3/4 дм. У воду занурили  куб. Знайти довжину ребра куба, якщо відомо, що він ліг своєю нижньою гранню на дно посудини і при цьому рівень води в посудині зрівнявся з верхньою гранню куба.

Розв'язання:

Нехай х дм - довжина ребра куба, тоді х³ дм³ - його об'єм. Об'єм води в посудині становить 3/4 * 4 = 3 дм³. Після того як у воду занурили куб, об'єм всієї місткості посудини дорівнює 4х дм³, тобто отримаємо рівняння х³ + 3 = 4х, або х³ - х - 3х + 3 = 0.                  (х - 1)(х² +х-3)=0. Тоді х₁ = 1,

Задачу задовольняють тільки х₁ і х₂.

2. Катер і пароплав відплили одночасно від пристані А в розміщену нижче вздовж течії пристань В, розпочали рейс між А і  В. За один робочий день катер 5 разів пройшов від А до В і від В до А, а пароплав за той самий день здійснив 9 таких рейсів. Знайти тривалість робочого дня, якщо відомо, що перша зустріч катера з пароплавом відбулася через 1/3 год. після початку руху, коли катер пройшов 5/6 відстані від А до В.

Розв'язання:

Швидкість катера за течією річки 5/6⃒АВ⃒:1/3=5/2⃒АВ⃒ (км/год.). Відстань 5⃒АВ⃒ км він пройшов за течією за 2 год. Нехай проти течії на ту ж відстань катеру потрібно х год. Тоді його швидкість проти течії - 5⃒АВ⃒/х км/год., а тривалість робочого дня х + 2 год. Позначимо швидкість пароплава за течією і проти течії відповідно через у і z км/год. Оскільки різниця швидкостей катера за течією і проти течії дорівнює різниці швидкостей пароплава (кожна з цих різниць рівна подвоєній швидкості течії), то y - z = 5/2⃒АВ⃒ - 5/х⃒АВ⃒. За  1/3 год. пароплав пройшов шлях ⃒АВ⃒ за течією і шлях ⃒АВ⃒/6 проти течії. Звідси Робочий день пароплава продовжувався (год.), а такий самий робочий день катера склав (х + 2) год. Тому . Якщо ⃒АВ⃒=1, то 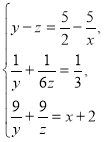Після перетворення отримаємох³+2х²–6х–32=0, (х+2)(х–4)(х+4)=0. Звідси х₁=4, х₂=–4, х₃=–2.Очевидно, що умову задачі задовольняє лише х₁, тому робочий день катера та пароплава 6 год.

Рівняння, які містять змінну під знаком модуля

На відміну від підручників, в яких показано використання формули відстані між двома точками координатної прямої, на факультативних заняттях корисно ознайомити учнів  з розв’язування більш складних рівнянь цього виду. Розглянемо декілька прикладів.

1. ⃒х+5⃒+⃒х-8⃒=16

Розв’язання:

На координатній прямій треба знайти точки, сума відстаней яких від точок х=-5 і х=8 дорівнює 16. Позначивши через у відстань, на якій знаходиться шукана точка зліва від точки х=-5, отримаємо допоміжне рівняння у+(у+13)=16 або у=1,5, тобто х₁=-6,5. На відрізку [-5;8] точок, які задовольняють рівняння нема. Справа від точки х=8, на відстані 1,5 знаходиться друга точка, яка задовольняє рівняння х₂=9,5. Відповідь -6,5; 9,5.

Використовуючи координатну пряму можна показати, що рівняння виду  ⃒х-а⃒+⃒х-в⃒=с, де с ≥0, при ⃒а-в⃒<с має два корені, причому вони не належать проміжку [а;в]. При ⃒а-в⃒=с рівняння має безліч коренів, причому розв’язком є проміжок [а;в]. При  ⃒а-в⃒>с рівняння коренів немає.

2. ⃒х+4⃒-⃒х-2⃒=5

Розв’язання:

На координатній прямі треба знайти точки, різниця відстаней яких до точок х=-4 і х=2 дорівнює 5. Оскільки відстань між точками х=-4 і х=2 дорівнює 6, то шукана точка належить проміжку [-4;2]. Позначивши через у відстань від шуканої точки до точки х = - 4, отримаємо у-(6-у)=5, або у = 5,5, тобто х = 1,5. Відповідь 1,5.

Порівнюючи відстані між точками числової прямої, легко показати, що рівняння виду ⃒х-а⃒-⃒х-в⃒=с, має один розвязок при  ⃒а-в⃒>⃒с⃒, тоді шукана точка належать проміжку [а;в]. При ⃒а-в⃒=⃒с⃒ рівняння має безліч коренів. При  ⃒а-в⃒<⃒с⃒ рівняння коренів немає.

У випадку, коли коефіцієнти при х відмінні від 1,їх можна винести за знак модуля, а потім розв’язувати рівняння відомим способом.

3. ⃒10-2х⃒-⃒8х-24⃒=0

Розв’язання:

Запишемо рівняння так: 2⃒х-5⃒-8⃒х-3⃒=0,або ⃒х-5⃒=4⃒х-3⃒. На координатній прямій треба знайти точки, відстані яких від точки х=3 були в 4 рази менші, ніж від х=5.

1. Нехай шукана точка не належить проміжку [3;5], а знаходиться зліва від точки х=3 на відстані у, тоді маєм рівняння: 4у=у+2, звідси у=2/3, тобто х=7/3.
2. Нехай шукана точка належить проміжку  [3;5] на відстані р від точки 3, тоді маємо рівняння 4р=2-р, звідси р=2/5, тобто х=17/5. Поза проміжком [3;5] справа від х=5 рівняння коренів немає.

Відповідь 7/3,17/5.

Складати допоміжні рівняння при розв’язуванні рівнянь, які містять змінну під знаком модуля не важко. Але важливо, щоб учні вміли перед розв’язуванням цих рівнянь знаходити проміжки, в яких є корені, і визначити скільки коренів має рівняння.

4. 

Розв’язання:

Запишемо рівняння у вигляді: ⃒х-1⃒+⃒х+2⃒=3. Оскільки            ⃒-2-1⃒=3, то розв’язком рівняння є весь проміжок [-2;1].

Відповідь [-2;1]

5. 

Розв’язання:

⃒х+3⃒=2⃒х+1⃒. Це рівняння має два корені х₁= –5/3, х₂=1.           Відповідь -5/3, 1

 

 

 

 

 

 

 

 

 

 

 

Розділ 4

Математичні гуртки

Математичні гуртки є основною формою позакласної роботи з математики. Заняття в гуртку доповнюють роботу на уроках і дають можливість задовольнити інтереси та запити учнів, які виходять за межі навчальної програми. Робота гуртків будується на основі знань, що їх набувають учні в процесі навчання, і тому її зміст включає:

• поглиблене вивчення найбільш цікавих питань навчального курсу;
• ознайомлення з діяльністю видатних історичних постатей, вчених, діячів культури;
• ознайомлення з новітніми досягненнями науки та техніки;
• проведення вечорів, присвячених ювілеям вчених та наукових відкриттів;
• організацію технічного моделювання;
• проведення дослідницької роботи учнями;
• організацію зустрічей з дослідниками, діячами науки та культури тощо.

У гуртках учні розширюють і поглиблюють набуті знання з математики, навчаються працювати над математичними проблемами, читати математичну літературу. Це сприяє підвищенню їх математичної культури, розширенню математичного кругозору і дальшому посиленню інтересу до математики.

 В діяльності математичних гуртків можна виділити два напрямки:

1. Формування і розвиток початкової цікавості до математики та розвиток математичного мислення;
2. Поглиблення і розширення знань з математики і теж розвиток математичного мислення.

Перший напрямок є провідним для гуртків учнів 5-7 класів, другий для гуртків учнів класів починаючи з восьмого, хоч елементи обох напрямків наявні в кожному з класів.

Ініціатором і організатором гурткової роботи з математики повинен бути вчитель. Він складає план роботи гуртка, виявляє учнів, які цікавляться математикою, і готує їх до участі в роботі гуртка, працює над посиленням їх інтересу до цього предмета.

На перше заняття вчитель запрошує всіх бажаючих, і після цього учень повинен вирішити питання про його участь в роботі гуртка; на цьому ж занятті проводиться вхідна бесіда, на якій керівник гуртка знайомить учнів зі змістом і планом роботи гуртка.

Перше заняття гуртка повинно бути типовим. Учні повинні зрозуміти, що такими ж будуть і наступні заняття. Заняття гуртка може бути побудовано за наступним планом:

Робота гуртка проходить ефективніше, якщо він об’єднує відносно стабільний склад учнів. Гуртківці залучаються до участі в шкільних вечорах, до  проведення  тижнів  математики,  до  випуску стінних газеттощо.

Заняття в гуртках (особливо учнів  5-7 класів) мають бути якомога жвавішими, з елементами гри, змагань, мають захоплювати учнів. Окремі завдання і запитання бажано добирати так, щоб труднощі, які виникають в процесі їх розв'язання, спонукали учнів до розгляду певних питань теорії і нових способів діяльності.

У роботі математичного гуртка велике значення має цікавість матеріалу і систематичність його викладу. Цікавість підвищує інтерес до предмету і сприяє розумінню важливої ідеї: математика оточує нас, вона є скрізь.

З огляду на це у зміст роботи гуртків варто включати ребуси, математичні фокуси і загадки, турніри й естафети, інсценівки, вікторини, математичні софізми, цікаві факти з історії розвитку математики і біографії видатних математиків тощо.

 

 

 

 

4.1. Матеріали на допомогу вчителю в           підготовці математичних гуртків

Крилаті вислови про математику

16.Арифметика - наче вхідна брама до всіх інших наук, бо без її пізнання ніхто не може зробити жодного кроку вперед до храму науки. (Феофан Прокопович)

17.Математику вже навіть задля того треба вивчати, що вона розум до ладу приводить. (М. В. Ломоносов)

18.Неспростовність - ім’я твоє, математика. (І. В. Куайн)

19.У математиці немає авторитетів. Єдиний аргумент істинності - доведення. (К. Урбанік)

20.Строгість у математиці означає насамперед добросовісність і ясність. (Ліпман Берс)

21.Адже незнайдеться нікого, хто б не захоплювався геометричними або оптичними чудесами. (Феофан Прокопович)

22. Математика приводить в порядок невпорядковане, викорчовує безглуздість, фільтрує брудне і дає ясність. (Жан Фабр)

23.У величезному саду геометрії кожний може підібрати собі букет за смаком. (Давид Гільберт)

24.Математика цікава тоді, коли живить нашу винахідливість і здатність міркувати. (Д. Пойа)

25.Хіба ти не помітив, що здібний до математики має успіх у всіх науках про природу? (Платон)

26.Математика настільки серйозний предмет, що не треба пропускати можливості зробити його цікавішим. (Блез Паскаль)

27.Рівняння та нерівності - золотий ключ, що відкриває всі математичні сезами. (С. Коваль)

28.Будь - яка наука тільки тоді досягає досконалості, коли вона користується математикоє. (К. Маркс)

29.У житті немає нічого кращого, як вивчати і викладати математику. (С. Д. Пуассон)

30.Математика вчить мислити й разом з тим вселяє віру в безмежні сили людського розуму. (В. О. Сухомлинський)

31.Жодне людське дослідження не може називатись істинною наукою, якщо воно не пройшло через математичні доведення. (Леонардо да Вінчі)

Задачі-жарти, задачі для кмітливих.

1. Казка

В Аравії помирав один старий. Все своє майно, 17 верблюдів, він заповідав синам, причому старший мав одержати половину, середній - третину, а найменший -дев'яту частину. Після смерті батька сини не знали, що робити, бо 17 не ділилося без остачі ні на 2, ні на 3, ні на 9.

Довго сперечалися брати, аж тут під'їхав до них на верблюді мудрець. Довідався про суперечку і дав братам мудру пораду, яка й допомогла розділити майно так, як заповідав батько. Що то була за порада?(Мудрець віддав братам свого верблюда. Верблюдів стало 18. Тоді їх поділили відповідно до батькового заповіту. Старший одержав 9, середній 6, молодший -2 В сумі дістали 17. А мудрець забрав свого верблюда й поїхав далі.)

2. П'ять хлібин

Один чоловік щодня купував п'ять хлібин. Приятель запитав його, що він з ними робить,

- Одну сам їм, двома борг сплачую, а дві в борг даю. Здивувався приятель і попрохав пояснити, що це значить.

(Який же ти нетямущий !! Одну сам їм, двома борг сплачую батькам за те, що вони мене годували, а дві дітям у борг  даю - потім вони мене годуватимуть.)

3. Скільки овець?

Жили собі два пастухи. У кожного по кілька овець. Перший пастух сказав другому:

- Давай мені одну вівцю і тоді в мене буде в два рази більше, ніж у тебе.

-Ні, - каже другий - давай ти мені одну вівцю, тоді в нас буде порівну. Скільки було овець у кожного?    (5 і 7).

4. Кому важче?

Кінь і осел, кожний окремо, везли мішки. Осел і каже:

- Ой, мені важко! А кінь йому:

- Ледарю, ти ще й скаржишся! Мені важче, ніж тобі. Якби я взяв у тебе один мішок, у мене стало б удвоє більше, ніж у тебе, а якби ти взяв у мене мішок, у нас було б порівну. Скільки мішків віз кінь і скільки осел? (5 і 7).

5.Переправа

Загін солдатів ішов до річки. Містка через річку не було, лише двоє хлопчаків плавали на човні. Однак човен був такий малий, що в ньому міг поміститися тільки один солдат. Як можна переправити через річку весь загін?

(Хлопчики поїхали до протилежного берега. Один з них лишився там, а другий повернувся до солдатів. Тепер мав змогу переправитись один солдат. Хлопчик, який залишився на протилежному березі, знову перегнав човен до загону. Потім обидва хлопчики переправилися на протилежний берег. Один з них залишився там, а другий переправив човен до загону і т. д.)

6. Цікаве число

Дівчинка записала на аркуші паперу число 666 і запитала подругу, чи зможе вона збільшити це число в півтора раза і відразу показати відповідь, нічого не записуючи. Подруга зразу здогадалася, як їй діяти. А чи здогадався ти? (Треба повернути аркуш паперу на 180°, матимемо число 999)

30.Череда

У пастуха, який вів 70 биків, запитали: "Яку частину биків своєї численної череди ти ведеш?" Він відповів: "Я веду дві третини від третини худоби". Скільки биків було у всій череді? (позначимо кількість худоби в череді через х, тоді за умовою задачі матимемо рівність: 2/3*(1/3*х)=70, звідки – 315 биків)

31.(З Бахшалійського рукопису)

З чотирьох жертводавців другий дав вдвічі більше, ніж перший, третій – втроє більше, ніж другий, четвертий – вчетверо більше, ніж третій, а всі разом дали 132 мішки золота. Скільки мішків золота дав перший?

(Нехай перший дав х, тоді другий – 2х, третій – 3(2х), четвертий – 4(3(2х)), отже х+2х+3(2х)+4(3(2х))=132. Відповідь:перший дав 4)

32.Яка вартість барана?

Кілька чоловік разом купують барана. Якщо кожний внесе по 5 монет, то не вистачить до вартості барана 45. Якщо кожний внесе по 7, то не вистачить 3. Скільки людей і яка вартість барана? (Нехай кількість людей – х, а вартість барана – y. Тоді y-5x=45;y-7x=3;відповідь:21 чоловік, а баран коштує 150)

33.Біля річки

Два чоловіки підійшли до річки. Біля берега стояв човен, в який міг поміститись тільки один чоловік. Все ж таки обидва туристи без будь-якої допомоги переправились на цьому човні через річку і продовжили свій шлях. Як вони це зробили? (двоє підійшли до різних берегів річки. Тому спочатку переправився один, а потім інший)

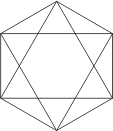34.Мозаїка з трикутників

Порахуйте, скільки трикутників у фігурі, яка зображена на малюнку: (32)

35. Один п'ятикласник про себе писав таке: "пальців у мене двадцять п'ять на одній руці, стільки ж на другій, на обох ногах 10." Як це так? (забув поставити дві крапки після двадцяти).

36.Яке натуральне число співпадає з кількістю букв в його найменуванні? (наприклад, три=3)

37. Як провести одну лінію в довільному трикутнику, щоб розбити його на чотири фігури? (вписати коло в трикутник) 38.Порада мудреця

Одного разу батько сказав своїм синам: «Осідлайте своїх коней, та їдьте з одного міста в інше. Чий кінь прийде до фінішу останнім, той одержить нагороду.» Сини сіли на коней і ледве плетуться. Назустріч мудрець, запитує в чому справа, чому вони так повільно їдуть. Ті розповідають. Він їм сказав усього два слова, й не пройшло хвилини, як вони вже скакали до фінішу щосили. Що він їм сказав?       (Поміняйтеся кіньми)

39. У підвалі

Є підвал, у якому знаходяться 3 лампочки. Вимикачі від цих лампочок перебувають поза підвалом так, що навіть при відкритих дверях у підвал, не видно чи горять лампочки. Як, увійшовши всього 1 раз у підвал, визначити, який з 3-х вимикачів, якій лампочці відповідає? (Включити дві будь-які лампочки, почекати якийсь час і виключити одну. Потім, зайшовши в підвал, побачимо одну лампочку, яка буде горіти. Торкнувшись двох інших, визначимо лампочку, що горіла. Вона буде теплою, а та, що не горіла - холодною. Отже, можна зіставити всі вимикачі.)

40. 9 монет

Є 9 монет. Є одні ваги. Терези звичайні, лабораторні (чашкові). Одна з 9 монет є легшою, ніж всі інші. Як визначити яка монета є легшою? Монети на вагах можна зважити лише 2 рази.

( Розділимо 9 монет по 3 монети в купці. Дві з 3-х купок покладемо на різні сторони терезів. Якщо терези не переважили в одну зі сторін, то виходить, що вага монеток є рівною й отже легка монета залишилася в незваженій 3-їй купці. З 3-мя монетами, що залишилися, вчиняємо так само. Зважуємо дві монети. Якщо їхня вага виявилася рівною, то легкою буде незважена монета.)

41.Із гнізда вилетіло 3-и ластівки? Яка ймовірніть того, що через 15 секунд вони будуть в одній площині? (100% - адже 3 точки завжди знаходяться в одній площині.)

 - Я завжди їду в п'ятому вагоні від хвоста потягу, — сказав Віталій.

- А я — у п'ятому від голови, — заявив Сергій. Скільки вагонів було в потязі?(9 вагонів)

63. Торговець купив деякий товар за 7 гривень, продав його за 8гривень, потім знову купив його за 9 гривень і знову продав за 10 гривень. Який прибуток він отримав? (2 гривні).

 

 

 

Прислів'я і загадки,

в яких зустрічаються числа

 

•     У березні сім погод надворі.
•     Влітку один тиждень рік годує.
•     Восени день блисне, а три кисне.
•     За одного вченого десять невчених дають.
•     Два хитрих мудрого не переважать.
•     Чи пан, чи пропав — двічі не вмирати.
•     Краще раз побачити, як тричі почути.
•     Ідеш на день - бери хліба на три дні.
•     Кінь на чотирьох і то спотикається.
•     Одна збрехала, друга не розібрала, а третя по-своєму переказала.
•     Сім п'ятниць на тиждень.
•     В роботі «ох», а їсть за трьох.
•     Де три, там і четвертому місце знайдеться.
•     І один у полі воїн.
•     Сім раз відмір, а раз відріж.
•     У семи няньок - дитя без нагляду.

 

1. Чотири грає, два танцює, один сидить і все чує. (Колеса, коні, візник)

2. Шість ніг, дві голови, четверо очей, один хвіст. (Вершник на коні)

3. В одної матері чотири дочки, а в кожної дочки не більше не менше,як п’ятнадцять дітей. (Година, чверть години, хвилина)

4. П’ятдесят два орли, а тільки одне яйце знесли. (Тижні, рік)

5. П’ять волів одним ралом оруть. (Пальці, перо, письмо)

6. П’ять, п’ятнадцять,

Без двох двадцять,

Семеро, троє

Ще й малих двоє.(П’ятдесят)

7. П’ять, п’ятнадцять,

Без двох двадцять,

Сорок, чотири,

Три і п’ятнадцять.(сто)

8.Сто кіп собак, скільки в них лап?(Двадцять чотири тисячі).

Вірші про математику

Якщо хочеш досягнути

У житті своїм вершин,

М а те ма т и ку  з б а г ну ти

Мусиш тонко, до глибин.

Калькулятор і комп’ютер,-

Хто сьогодні їх не зна?

Та  за  пояс їх запхнути

Може світла голова.

Якщо хочеш бізнесменом

 Після школи, друже,  стать,

 Аксіоми й теореми

Мусиш добре пам’ятать.

Якщо лікарем ти станеш,

То,  колего,  тут  затям

Коли десь  помилишся -

Хтось  поплатиться життям.

 Не кажу  про космонавтів,

Вчителів і моряків.

Та коли чогось не знав,

Час це вивчитинастав.

Не махай  на  все рукою,

Не лінуйся,  а учись

Бо чого навчишся  в школі,

Знадобиться ще  колись!

                       В  Математиці-країні

І сувора, й солов’їна

Математика-країна,

Праця тут іде завзята.

Вмій лиш спритно рахувати

Вмій ділити, віднімати,

Множить швидко й додавати.

Вмій кмітливо все збагнути.

Першим в відповіді бути!

Ледарів у нас немає,

Хто руки не піднімає?

Вирушаймо в путь-

Нас цікаві справи ждуть.

Цифри можна прочитати

І про все на свій знати:

скільки коксу домнам треба

Й про політ космічний в небо.

Скільки зір дрібних, як просо,

і веснянок є на носі.

Все умій ти пов'язати,

Про складне й просте сказати.

Наш девіз - все гарно знати,

ВМІТИ добре рахувати.

Виростаймо ж - і у путь.

Хай знання із нами йдуть.

Ну а потім, в результаті,

Все, як слід, підсумувати.

Й розділити на усіх,

І багатство, й щедрий сміх.

       Ода цифрам

Яскравим сонцем, щедро вмиті

Знаменні цифри історичні.

Вони, немов розквітлі віти,

Ласкаво дивляться в обличчя.

Хто каже — цифри безсловесні?

Вони ідуть назустріч веснам.

В далекій тундрі і аулі

Ми їхню мову всюди чуєм.

Звучать вони, як пісня слави,

Як велич нашої держави.

В них мрія серця ожива,

У них дерзань палкі слова.

То тріпочуть, як листочки,

То шикуються в рядочки.

Вони в перебігу гудків,

В роботі річок і полів.

Дарма, що цифри без прикрас,

Вони — змагання наше й сила

У необхідний, скрутний час,

До щастя зоряного крила.

Вірш-жарт про степені числа 2

Слон  живе у нас вквартирі —

Поверх 2, під'їзд - 4.

Звик він часто харчуватись:

Вранці в 8, вдень - в16.

На сніданок неодмінно –

32 обремки сіна.

Це водоюслід запити —

64 літри.

На обід даємо рису,

Огірків 128,

Помідори також їсть —

250 і 6.

З'їсть млинців 512

Це якшо не постаратись,

А як  зробиш на кефірі – 1024.

НУЛЬ 

                                             (С.Маршак)

Ось круглий нуль, або нічого.

Послухай казочку про нього.

Веселий нуль прошепотів

Сусідці-одиниці:

— З тобою поруч я б хотів постояти, сестрице!

Та одиниця каже: «Ні, ти — нуль, число нікчемне.

Не стій зі мною, бо мені це зовсім неприємно!»

А нуль на це: «Я знаю сам, що в світі значу мало...

Та якби поруч стати нам, десятка б з тебе стала!

Поглянь на себе — ти ж у нас мала та худорлява.

Нехай не кажуть, що нулі такі нікчемні та малі:

Із двійки — двадцять зробим ми,

Із трійки — зробим тридцять,

З четвірки — сорок, а з семи — аж сімдесят, дивіться!»

Отож, хоч нуль -ніщо й ніхто, та два нулі на місці

Із одиниці зроблять сто,

А з двійки — цілих двісті!

МАТЕМАТИКА

Ти визнана давно главою всіх наук –

Потрібна нам ти скрізь, завжди і всюди.

Без математики ми нині, як без рук.

З тобою з казки дійсність творять люди.

 Освоївши тебе – рвемося у політ.

 Створили вже розумні ми машини,

 Штурмуємо космічний світ

 І різних фактів визнаєм причини.

З тобою ми невпинно ростемо,

З тобою – підкоряємо природу.

Твої досягнення ми віддамо

На благо рідного народу.

 Сьогодні ви прийшли в цей зал

 Подумати, помріять, відпочити.

 Побачити гру і бал

 І розумом своїм все охопити.

Згадаєм нині формулу Герона,

Яку ти вже не раз писав,

Згадаєм також і Ньютона,

Біном якого пізнавав.

 Хай в пам’яті воскресне Архімед,

 Що за творіння славлений велике,

 Відомий всім згадається Вієт,

 Що формулу рівнянь зумів відкрити.

Відомий обдарований Декарт –

Творець координатної системи.

І Лобачевский всіх учених брат,

Та скульптор геометрії – Копернік.

 І нині славний Чебишов-титан,

 Софія Ковалевська – наша прима.

 Могутній їм даровано талант,

 Їх розум – непохитна брила.

 

Думок великих та ідей творці,

Що рід людський виношував століття,

Крізь бурі перейшовши дні важкі

Переживуть тепер тисячоліття.

 Запам’ятай, що Гаусс всім сказав:

     “Є математика царицею наук”.

 І недаремно він заповідав

 Творити в вогнищі робіт і мук.

Безмежна роль її у відкритті законів,

У створенні машин – повітряних, земних.

І було б важко нині без Ньютонів,

Що дала нам історія до наших днів.

 Нехай не станеш Піфагором ти,

 Яким у мріях вирости бажаєш.

 Та будеш ти людиною завжди

      І Україну вславиш добрими ділами.

МАТЕМАТИЧНІ ЧАСТІВКИ

Ми веселі дві подружки,                       

Із баяном-братиком                             

Заспіваємо частівки                            

Вам  про математику.

Та невже ми заспіваєм                         

Вам про математику?  

     

Знають Ігор, Коля й Вася,                    

Що в них з алгебри у класі                    

Іспит наближається.                                                          

А в щоденнику й журналі

Двійки прибавляються.

Та невже ото насправді

Двійки прибавляються?

 

Отака в усіх нас доля,   

 Іспити — страждання:

Не дозволять нам списати

3 алгебри завдання.

Та невже не зможем справді

Списати завдання?

 

Розв'язав Петрусь задачу,

Тільки мінуса не бачив,

От і сталось, що лимон

Важить майже 8 тонн.

 Та невже ото лимон

Важшпь справді 8 тонн?

 

На контрольній ловив гав,

Одиницю упіймав,

 Підглядав в усі книжки —

Переплутав сторінки.

Та невже ото таки

Переплутав сторінки?

 

Біля дошки він стояв

 І придумав чудо:

 В теоремі прирівняв

 До квадрата куба.

 Та невже ото квадрата

Прирівняв  до куба?

 

Хто задач не полюбляє,

 Тим така і дяка:

 Весь рік двійки заробляє

Й вийде лобуряка.

Та невже ото подяка:

 Двійки в лобуряки?

 

 

 

 

 

 

 

 

 

Розділ 5

Позакласна робота з математики

Характеристика   напрямків   позакласної роботи з математики.

Виходячи з того,  що позакласна робота повинна бути диференційована, спрямована на задоволення інтересів і запитів учнів, а учні мають різні здібності та інтереси, тому треба розрізняти три напрямки позакласної роботи з математики:

1.                     робота з учнями, які не досягли обов'язкового рівня у вивченні програмного матеріалу (додаткові позакласні заняття);
2.                     робота з учнями, які бажають підвищити свій рівень навчальних досягнень з певної теми;
3.                     робота з учнями, що виявили до вивчення математики підвищений інтерес та здібності (це позакласна робота у традиційному розумінні). 

1) Говорячи про перший напрямок, відзначимо, що цей вид позакласної роботи з математики у теперішній час має місце в кожній школі. Разом з тим підвищення ефективності навчання математики на уроках повинно з часом привести до зниження значення додаткової роботи з відстаючими. Але зараз ця робота вимагає від учителя математики багато зусиль та уваги.

Головна мета її – своєчасна ліквідація (та попередження) прогалин у знаннях, уміннях і навичках учнів з курсу математики.

Роботу з такими учнями найкраще проводити індивідуально, бо прогалини в знаннях учнів різні. Проте можна вказати теми, які важко засвоюються багатьма. За такими темами варто проводити групову роботу.

Завдання для цих учнів повинні бути посильними для них, по можливості, мати практичний характер, викликати інтерес, містити підказки, зразки розв'язань, малюнки.

Досвід роботи показує, що для розуміння і відтворення розв'язання, учневі треба розв'язати по 2-3 майже однакових задач. Працюючи з учнями, треба пам'ятати, що будь-який бал, що набрала дитина, має розглядатись як позитивний результат.

2) Зупинимося на другому напрямку позакласної роботи.

Це новий напрямок у додатковій роботі з учнями і не дуже розроблений у методичній літературі, бо приходять підвищити свій рівень навчальних досягнень і учні, які мають 5, 7, 8, 9 балів.

Я думаю, що в цьому випадку треба:

а) передивитись з учнем його тематичну залікову роботу;

б) перевірити роботу над помилками, зроблену учнем;

в) відповісти на запитання, які з'явилися в учня у процесі виконання тематичної роботи та роботи над помилками до неї;

г) дати можливість учневі порозв'язувати відповідні завдання з "Дидактичних матеріалів" та тестів;

д) провести тематичну роботу та виставити відповідну кількість зароблених балів.

3)Роздивимось третій напрямок: робота з учнями, що виявили до вивчення математики підвищений інтерес та здібності.

За формами організації ця позакласна робота з математики теж поділяється на масову, групову та індивідуальну. Кожна з них має свої переваги і недоліки. Масова робота дає змогу залучати до неї великий колектив учнів. У такому масовому вияві творчості легко організувати змагання, проте важко забезпечити глибоке проникнення всіма учасниками в суть розглядуваних математичних залежностей, проконтролювати діяльність кожного учасника. Зрозуміло, що важко й підтримувати тривалий час продуктивну роботу великого учнівського колективу.

Більш результативною є робота з невеликою групою, як правило, тих самих учнів, наприклад, членів математичного гуртка. Індивідуальна робота проводиться тут відповідно до інтересів учнів.

У проведенні позакласної роботи з математики треба враховувати вікові особливості учнів. Таку V-VІ класах доцільно розглядати цікаві питання теоретико-числового і геометричного матеріалу. Проте слід пам’ятати, що розвага – не самоціль, а тільки один з дидактичних прийомів, який стимулює пізнавальну активність учнів. Розважальний матеріал збуджує увагу, викликає певні позитивні емоції та ситуаційний, епізодичний інтерес. Завдання учителя - перетворити цей інтересу стійкий, активний.

Використовуючи розважальний матеріал, треба звертати увагу учнів не на зовнішні факти, а на суть питання, будити думку, розвивати допитливість.

 

 

Традиційними і найбільш поширеними формами позакласної роботи з математики є:

•                    математичні гуртки;
•                    математичні вечори, КВК;
•                    математичні вікторини;
•                    математичні турніри;
•                    математичні естафети;
•                    математичні стінгазети;
•                    математичні олімпіади;
•                    позакласне читання з математики;
•                    математичні екскурсії.

Ці форми роботи опрацьовані в кожній школі, але зараз, щоб активізувати позакласну роботу, вчителі шукають і знаходять нові форми позакласної роботи з математики:

•                    конкурс "Нумо, математико";
•                    гра "Математичний бій";
•                    математична вікторина "Що, де, чому?";
•                    математичний хокей;
•                    математичний цирк;
•                    подорож з математикою;
•                    математичний ярмарок;
•                    "Брейн - ринг";
•                    гра "Поле чудес";
•                    гра "Щасливий випадок";
•                    гра "О, щасливчик!", тощо.

Математичні твори

Ця форма позакласної роботи може бути проведена як з членами гуртка, так із кожним учнем класу. Вчитель пропонує ряд тем і закріплює одну з них за кожним учнем. Краще коли він дає всім різні теми. В окремих випадках можна допустити і їх повторення. Учням, залежно від змісту теми, він пропонує написати твір протягом півріччя.

Вчитель повинен старанно підготувати список літератури до кожного з творів і допомагати учневі скласти його план. У деяких випадках учень підбирає літературу і складає план самостійно. На найбільшу увагу в творі заслуговують самостійно складені і розв'язані задачі, доведені теореми та ін.

Переглядаючи і оцінюючи математичні твори, вчитель може запропонувати учню розширити власну роботу, взявши участь у конкурсі робіт серед учнів членів МАН України.

Математичні вікторини

Математичну   вікторину   здебільшого   проводять   на   математичних вечорах і рідко практикують як самостійний захід у позакласній роботі. У   вікторині   можуть   приймати   участь   усі,   хто   бажає.    Пропонують здебільшого 6-12 запитань і задач. Вікторину, залежно від числа учасників, можна проводити по-різному.

Перший варіант. Кожне запитання або задачу зачитує вчитель чи учень, який проводить вікторину. На обдумування відповіді дається декілька хвилин. Відповідає той, хто перший підніме руку. Якщо відповідь неповна, то можна дати можливість висловитись ще одному учаснику вікторини. За повну відповідь присуджують два бали, за неповну, але задовільну - один бал.

Переможцями вважаються ті учасники вікторини (2-4 учня), які набрали найбільшу кількість балів. Окремі задачі і запитання лише зачитують, умови інших задач можуть бути записані на дошці. Так можна проводити вікторину, коли в неї беруть участь порівняно небагато (50-60) учнів.

Другий варіант. Якщо у вікторині бере участь багато (100-200) учнів, то її проводять так.

Тексти всіх запитань і задач набирають на комп'ютері і роздруковують на окремих аркушах, які роздають учням. Крім того кожному учасникові видають аркуш чистого паперу, на якому він записує відповідь та коротке пояснення до кожного запитання і задачі, а також своє прізвище, ім'я, клас. Цей аркуш він здає жюрі вікторини. Через певний час після початку вікторини (наприклад, через 30 хв) приймання аркушів від учасників вікторини припиняються. Жюрі перевіряє розв'язання і виявляє переможців. До жюрі вікторини входять звичайно 5- 7 членів гуртка. З гуртківців вибирають також ведучого вікторини.

Переможцям видають нагороди (найчастіше книги з математики).

Бажано, щоб запропоновані на вікторині задачі і запитання були хоча б частково розібрані. Не можна перетворювати вікторину на олімпіаду. Олімпіада є набагато відповідальнішою формою змагань. Тривалість вікторини — не більше як 25-40 хв.

Задачі для вікторини повинні бути невеликими, доступними для усного розв'язування. Крім задач, у вікторину можна включити також різні запитання з математики або з історії математики.

У вікторину включають також задачі-жарти. Її можна присвятити повністю якій-небудь одній темі, наприклад, прийомам раціональних обчислень, арифметичним задачам на міркування та інше, але найкраще пропонувати комбіновані запитання.

Математична олімпіада

Шкільна математична олімпіада є важливою формою позакласної роботи, її завдання — підвищити інтерес учнів до вивчення математики, поглибити їх теоретичну підготовку, вплинути на розвиток їх творчих здібностей, виявити юних аматорів математики, щоб залучити їх у подальшому до наукової роботи.

Разом з тим математичні олімпіади мають і виховне значення. Вони привчають учнів до організованості, зміцнюють волю до перемоги, виробляють самостійність і чіткість мислення.

На олімпіаді дають розв'язати задачі і приклади в обсязі програми з математики відповідного класу. Проте умови задач і їх зміст нестандартні. Щоб розібратися в них, учасникам треба вміти мислити, мати добре розвинуту геометричну уяву, знати найраціональніші перетворення іт.д.

У число задач до олімпіади можна включити одну таку, яку могла б розв'язати більшість учасників. Надміру складне завдання може породити в учня невіру в свої сили і відбити бажання займатися математикою. Але водночас доцільно давати й складніші задачі, щоб з усієї маси учасників виділити найбільш підготовлених. Найкраще пропонувати 3-5 задач різної складності нестандартного змісту. Кожну запропоновану задачу оцінюють певною кількістю балів. Звичайно, оцінюючи роботу, слід брати до уваги якість її оформлення, оригінальність і раціональність розв'язання.

Математичні  вечори

Математичний вечір — одна з масових форм позакласної роботи, яка сприяє поліпшенню якості знань учнів з математики, вихованню в них інтересу і любові до цього предмету. Він є своєрідною формою звіту про роботу гуртків перед усім колективом школи.

За рік можна провести 1-2 математичні вечори. Підготовка і проведення цього заходу потребує великої роботи вчителів математики і членів математичного гуртка. Вчитель розподіляє завдання між гуртківцями, Учні працюють над завданнями, одержують відповідні поради від вчителя. Якість підготовки до вечора перевіряється на засіданні гуртка. Про день проведення вечора повідомляють у красиво оформленому оголошенні, в якому подають і його програму.

Вечір може вести вчитель. Він оголошує про черговий виступ і дає коротке пояснення до нього. Але краще, якщо ведучими будуть учні. Вони можуть не тільки оголошувати про виступ, але і самі виконувати деякі завдання.

Майже завжди вечір складається з двох відділень, між ними влаштовується перерва на 10-20 хвилин. Під час перерви, а також на початку вечора школярі можуть ознайомитися з експонатами та плакатами.

На математичному вечорі нерідко використовуються математичні фокуси. Більшість таких фокусів пов'язано з "відгадуванням" чисел. Математичною  основою такого фокуса є деяка алгебраїчна тотожність. Кожен раз, розглядаючи математичний фокус, необхідно довести до учнів математичну сутність фокуса. Без цього освітня цінність фокуса незначна. Краще всього, якщо учні самі знайдуть тотожність на якій грунтується фокус. В основному розгадування подібного роду фокусів пропонують учням 7-8 класів.

Математичні тижні

Тижні математики дають змогу залучити до позакласної роботи багатьох учнів усіх класів, розкрити їхні потенційні здібності, підвищити рівень математичної культури, розвити пізнавальний інтерес учнів, розширити їх кругозір, показати роль математики в науково-технічному прогресі і в розвитку інтелектуального потенціалу країни. Ця форма роботи насичена конкретними заходами, і тому успішне проведення “Тижня математики” вимагає серйозної і тривалої підготовки.

 

 

 

Висновки.

 

Сучасна педагогічна практика закономірно ставить питання зміцнення взаємозв'язку факультативних занять з класними та позаурочною роботою, подання учням допомоги у свідомому виборі факультативних курсів.

Дуже бажано, щоб зусилля вчителів, спрямовані на позакласну роботу, відбивалися на наслідках навчання математики. Важливо забезпечити таку взаємодію між класними, факультативними та позакласними заняттями в школі, щоб весь навчально-виховний процес був єдиним цілим, коли класні та позакласні заняття, зберігаючи свої специфічні особливості, цілеспрямовано впливали один на одного, сприяючи підвищенню спільної ефективності навчання, виховання та розвиток школяра.

Навчання математики в школі треба будувати так, щоб воно було для учня серією маленьких відкриттів. По будь-якому розділу з математики можна скласти завдання, виконання котрих дійсно би містило елементи творчості.

Знання ж учнів будуть міцними, якщо вони здобуті не тільки однією пам'яттю, не завчені механічно, а з'явилися внаслідок власних міркувань, та закріпилися у їх власній творчій діяльності з навчальним матеріалом.

Учні повинні розв'язувати задачі з конкурсних збірників, готуватися до шкільних олімпіад, читати науково-популярну літературу. Самостійна робота учня носить пошуково-дослідницький характер і потребує творчих зусиль: учні самостійно розв'язують задачі, сформульовані ними або подані вчителем.

Найбільш глибоко та повно система навчальної роботи по розвитку самостійності і творчої активності школярів реалізується при вивченні факультативних курсів з математики.

 

Бібліографія

 

1.  М.П.Гузик, М.І.Жалдак, В.М.Монахов, М.І.Шкіль, Т.Б.Волобуєва.  «Розв’язання творчих завдань»

2. Д.А.Балл, Т.Гергей, А.М.Довіяло, І.П.Підласий, С.Смірнов «Впровадження розвивальних творчих ігор»

3. Ю.К. Бабанський, X.І.Лійметс, І.Унт, Є.С.Рабунський, І. М.Чере- дов, О.О.Кірсанов, С.І.Подмазін. «Індивідуальний підхід у навчанні»

4. Ю.К.Бабанський, Д.В.Вількєєв, М.О.Данілов, І.Я.Лернер, М.Махмутов «Проблемний підхід»

5. С.Г.Шаповаленко, І.І.Тихонов «Самостійна робота творчого характеру»

6. Л. П.Пресман, Е.Е.Соловйова, М.М.Шахмаєв «Впровадження технічних засобів навчання»

7. Богданов М. «Цікава математика» //Позакласний час. №3.

8. Боровикова В. «Аукціон знань» //Математика №42.