Задачи з параметрами – перше знайомство

 Задачи  з параметрами – перше знайомство

Рівняння з параметрами трапляються кожного року серед завдань зовнішнього незалежного оцінювання з математики. Але  оскільки шкільна програма не передбачає набуття стійких навичок розв’язання таких рівнянь учнями, то вчителю необхідно поступово все ж таки вводити такі завдання.

    Вміння розв′язувати задачи з параметрами дає змогу оцінити знання учнів основних розділів шкільної математики, рівня математичного та логічного мислення.

  Перше знайомство з параметрами треба починати з 5 , 6 класу. Основне, що потрібно при першому «знайомстві» з параметром, - це пояснити обережне, навіть делікатне поводження до фіксованого, але невідомого числа. Тому перше «знайомство» необхідно робити з задачами, де заміна параметра числом  робить задачу банальною. Це треба поступово починати з 5 класу.

Рівняння з параметром - це по суті, короткий запис сімейства рівнянь. Рівняння цього сімейства виходять з даного рівняння при різних конкретних значеннях параметра а.

5 клас.  Автори підручників пропонують вправи , які сприяють підготовці учнів до розуміння  задач з параметрами.

Наприклад.

1. При яких натуральних значеннях а є правильною нерівність 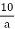> а. ліва частина якої неправильний дріб?

Розв′язання.   Дріб , отже а ≤ 10, тобто 1,2,3,…,10. Треба розглянути кожен з випадків. Якщо а = 1, то > 1, 10 > 1нерівність вірна. 

                               Якщо а = 2, то > 2, тобто 5 > 2, нерівність вірна.

                              Якщо а = 3, то > 3, тобто > нерівність вірна.

                               Якщо а = 4, то > 4, тобто > нерівність невірна.

                               Якщо а = 5, то > 5, тобто 2 >  5, нерівність невірна.        

                                Якщо а = 6, то > 6, тобто > нерівність невірна.

                                 Якщо а = 7, то > 7, тобто > нерівність невірна.

                              Якщо а = 8, то > 8, тобто > нерівність невірна.

                              Якщо а = 9, то > 9, тобто > нерівність невірна.

 Якщо а = 10, то > 1, нерівність невірна.

Відповідь. а =1,2,3.

2. Яке число треба підставити замість а, щоб коренем рівняння (х + а) – 7 = 42 було число 22.

Розв′язання. х = 22, тоді (22 + а) – 7 = 42, а = 42 + 7 – 22 = 27. Перевірка (22 + 27) – 7 = 42.

Відповідь: якщо а = 27, то корінь рівняння х = 22.

  В 6 класі дальше продовжуємо розвʼязувати  завдання рівнянь з параметром. Автори підручників «Математика»  6 клас допомагають вчителям спланувати системне вивчення цього матеріалу. Ці вправи носять дослідницький характер, вимагають від учнів високого рівня знань.

Наприклад. 1) Порівняйте b і 4b.

Розв′язання.   Якщо b < 0, то b > 4b,

                         якщо b > 0, то b < 4b,

                         якщо b = 0, то b = 4b.

2) Розв′язати рівняння ах = 1.

На перший погляд відповідь - х = . Але якщо а = 0, рівняння не має розв′язків. Тому

відповідь треба записати так: якщо а = 0, то рішень немає; якщо а

  В 7 класі розпочинається вивчення курсу алгебри і тут вже даються «справжні» рівняння з параметром. Системне знайомство з параметром починається в 7 класі коли вивчають лінійне рівняння ах = в. Схема розв'язання лінійного рівняння виду ах = b.

                                                       Якщо

                                                 а 0       а = 0

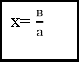
                                                                                                   якщо

                1 корінь                                    в 0    в = 0

Розглянемо приклади простих типових рівняння з параметром.

1. (а – 3)∙х = 5.

Відповідь: якщо а ;

                   якщо а = 3, то рішень немає.

2. ах – 2х = 3(х + 1).

ах – 2х = 3х + 3, ах – 2х – 3х = 3,  ах – 5х = 3, (а – 5)х = 3,

Якщо а = 5, то 0∙х = 3, рішень немає;

якщо а .

= 0.  Область визначення  дробі х + 3. Дріб дорівнює нулю, коли х – а = 0. Тому х = 0.

Відповідь: якщо а ;

                  якщо а = - 3, то рішень немає.

= 0.    Область визначення  дробі х + а. х = 3,

якщо х

Відповідь: якщо а ;

                  якщо а = - 3, то рішень немає.

= 0. Область визначення  дробі а – 3 , х – а = 0, якщо а .

Відповідь: якщо а 3, то х = а;

                  якщо а = 3, то  рішень немає.

Після цих рівнянь можна розглянути більш складне.

6. 2а(а- 2) х = а – 2.

Нехай область змінення параметра а є -, тоді маємо сімейство рівнянь:

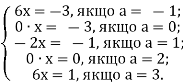
       А, якщо а – будь-яке число? Ясно, що виписати кожне рівняння з нескінченного сімейства рівнянь неможливо. Проте кожне рівняння сімейства має бути вирішено. Зробити це можна, якщо, наприклад, за деякою ознакою розбити безліч всіх значень параметра на підмножини і вирішити потім задане рівняння на кожному з цих підмножин. Для розбиття значень параметра скористаємося тими значеннями, при яких або при переході через які відбуваються якісні зміни рівняння.

     В цьому рівнянні це – значення параметра при якому коефіцієнт при х дорівнює 0. Такими є значення а = 0 та а = 2. Якщо а = 0 та а = 2, то неможливо ділення кожної частини рівняння на коефіцієнт при х. В той же час, якщо а то ділення можливе.

Тому розглянемо розв′язування рівняння, якщо 1) а = 0; 2) а = 2; 3)

1. Якщо а = 0, рівняння має вигляд 0∙х = - 2, рівняння коренів не має.
2. Якщо а = - 2, рівняння має вигляд 0∙х = 0, коренем буде будь – яке число.
3. Якщо а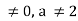, тоді х = 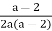, звідки х = .

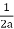Відповідь: якщо а = 0, то коренів немає;

                 якщо а = 2, то х – будь-яке число;

                  якщо то х = .

7. ( – 1)∙х = а +1.

При розв′язуванні цього рівняння достатньо розглянути такі випадки:

1) а = 1, тоді    0∙х = 2, коренів немає;

2) а = - 1, 0∙х = 0, х – будь-яке число;

3) - 1, а 1, х = .

Відповідь: якщо а = - 1, то х – будь-яке число;

                    якщо а = 1, то коренів немає;

                     якщо - 1, а 1, х = .

    Важливим етапом рішення завдань з параметром є запис відповіді. Особливо це відноситься до тих задача, де рішення як би «відкується» залежно від значень параметра. У подібних випадках запис відповіді - це збір раніше отриманих результатів. І тут дуже важливо не забути відбити у відповіді всі етапи рішення. Так в останньому прикладі запис відповіді практично повторює рішення. Проте, його необхідно привести.

   Часто зміст математичної задачі с параметрами не виходить за межі шкільної програми, але учні не готові розв′язувати такі задачі без попередньої підготовки. Досвід підказує, що починати знайомство з параметрами  треба як раніше, і частіше повертатися до таких задач протягом усіх років навчання.

Література

1.  Горнштейм П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. – К.: РИА «Текст»; МП»ОКЛ», 1992.–290с.
2. Доманська І.П., Зеліско Г.В., Стахів Л.Л. Рівняння з параметрами: Методичні рекомендації.- Львів: Видавн. центр ЛДУ ім. І. Франка, 2005.
3.   Крамор С.В. К78 Задачі з параметрами і методи їх розв’язання. — Тернопіль: Навчальна книга – Богдан, 2011. — 416 с.                                                                                                 4. Кушнир И.А. Шедеври школьной математики. т.1, т.2. –  К.: «Астарта», 1995.–510с.

      5. Сержук С.В. Рівняння з параметрами // Математика в школах України, № 17-18,   2004.

6. Мерзляк А. Г., Полонський В. Б., Якір М. С. Математика 5,6 клас, Алгебра 7 клас