Найпростіші перетворення графіків функцій

Тема. Найпростіші перетворення графіків функцій

 

Мета:

•  навчальна: удосконалювати навички перетворення графіків функцій та побудови графіків функцій з використанням перетворень графіків; за поданою формулою визначати графік функції та його назву; сформувати  навички побудови графіків функцій, використовуючи програму GRAN1;
• розвивальна: Інформаційно-комунікаційна компетентність

• впровадження інформаційно - комп’ютерних технологій навчання;
• залучення учнів до роботи з різними джерелами інформації;
• розвивати навички роботи учнів на комп’ютері.

• виховна: Соціальна компетентність

• використання групових, парних форм організації навчальної діяльності;
• упровадження технологій і методів навчання, що сприяють формуванню правильної оцінки і самооцінки, умінь застосовувати власний досвід, адаптуватися до змін.

                Громадянська компетентність

• вчити учнів аргументовано доводити власну точку зору.

Наскрізна лінія «Громадянська відповідальність»:

виховувати увагу, активність, естетичний смак, почуття єдності та відповідальності за спільну справу.

Обладнання: мультимедійний проектор; презентація; картки самоконтролю, завдання для гри «Математичне доміно»; шаблони графіків функцій; опорний конспект.

Очікувані результати: учні повинні знати правила перетворень графіків функцій: f(x)→f(x)+a, f(x)→f(x+a), f(x)→kf(x), f(x)→ - f(x), ; уміти будувати графіки функцій, застосовуючи відповідні перетворення.

 

Тип уроку: узагальнення знань і вмінь.

 

Хід уроку

І.Організаційний етап

     -  Вітаю рада новій зустрічі з вами.   Ідучі до вас на урок , згадала одну притчу про філософа Сократа.

      - Одного дня Сократ, оточений учнями, піднімався до храму. Назустріч їм спускався пекар з різною здобою. “Сократ, а чи пишаєшся ти своїми учнями? – запитав пекар. Так. – відповів Сократ. Послухай, варто лише мені задобрити їх здобою, як вони покинуть тебе і підуть зі мною”. На що  мудрець відповів: “Згоден, але ти гукаєш їх вниз, в теплу смачну  долину, а я веду їх вгору, до непереборних, чистих вершин”.

Ось і ми повинні піднятися на сходинки вгору, “долаючи” завдання, які будуть розглянуті на сьогоднішньому уроці,

Зараз ми знаходимося на першій сходинці, але я впевнена, що разом ми зможемо здолати будь-які вершини.  Хочу вам нагадати, що знання  формуюься у нашій уяві тож пропоную вам вправу АК

 

ІІ. Актуалізація опорних знань

І. Інтерактивна вправа «Асоціативний кущ» https://learningapps.org/watch?v=ppk40chon20

     -  Які поняття асоціюються у вас з терміном  «Функція», а які з темою «Нерівність» (Аргумент, значення функції, область визначення, область значень, способи задання функції: словесний, аналітичний, графічний, табличний; нулі функції, проміжки зростання і спадання функції; числові нерівності; система нерівностей; розв’язок нерівності; числовий проміжок).

 

ІІ. Робота в парах. Гра «Математичне доміно»

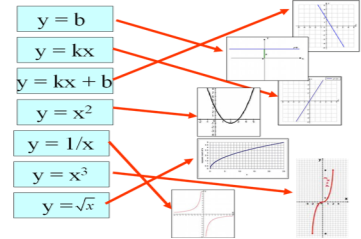
  Учням на парти роздаються «доміношки» - картки із функціями, їх назвами і графіками.  Суть гри полягає в тому, щоб виконуючи це завдання вам потрібно скласти відповідність функція        назва        графік та прочитати закодоване слово. Працювати ви будете в групах, допомагаючи один одному.

 

1. Встановіть відповідність

 

 

 

 

 

 

 

 

 

 

 

 

 

Правильна відповідь «Уміння» .

Усе у світі рухається, усе змінюється, нічого не стоїть на місці. Повертається навколо своєї вісі Земна куля, і день змінює ніч, Земля обертається  навколо Сонця, Сонце разом зі всіма своїми планетами вічно прямує у космічні далі. Рослини, дерева ростуть по своїх траєкторіях.

• Здається, до чого тут  функції, і графіки? Саме функція є тим засобом математичної мови, який дозволяє описувати процеси руху, зміни  неповторної краси, що належать природі. Починаючи із XVІІ ст. функція є одним із основних математичних питань. Це поняття і донині відіграє значну роль у розумінні реального світу.

- Отож, сьогодні на уроці ми спробуємо на практиці реалізувати набуті уміння з вивченої теми.

Пропоную переглянути ще один ролик.

 (Перегляд відеоролика)???

 Що саме  відображає ролик?

Так, дійсно він відображає графіки функцій, а також функціональні залежності. А ще дозволяє розкрити красу графіків через  створені людиною будівлі, візерунки.

Я згадала слова Костянтина Феофановича Лебединцева, які я хотіла б взяти епіграфом нашого сьогоднішнього уроку.

Епіграф уроку:

                                   Немає жодної галузі людських знань, куди б не    

                                 входило поняття функції та її графічного зображення.

                                                                                                        К.Ф.Лебединцев

 

 

Тож записуємо число, класна робота та тему нашого уроку   «Найпростіші геометричні перетворення графіків функцій».

 

 ІV. Узагальнення, систематизація знань.

Тож давайте згадаємо як побудувати графік функції у=f(x) +а за допомогою знайомих вам ресурсів.

ПИСЬМОВО

1. Паралельне перенесення  вздовж осі ОУ на

а одиниць ( якщо а>0, то вгору, якщо а<0, то вниз).

Побудувати графік функції  у=√х +4

Побудувати графік функції у=√х – 3

 

 

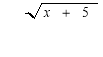2. Паралельне перенесення  вздовж осі ОХ на а одиниць ( якщо а>0, то ліворуч, якщо а<0, то праворуч).

Побудувати графік функції  у=

 

3. Симетрія відносно осі ОХ. у= - √х

    

     4. Побудувати графік функції 

 

V. Узагальнення, систематизація  вмінь та навичок.

На сьогодні розроблено значну кількість програмних засобів, що дозволяють розв’язувати досить широке коло математичних задач за допомогою комп’ютерів. Це прикладні програми навчального призначення. Сьогодні на уроці ми скористаємося однією з таких програм, яка дуже спрощує процес побудови графіків функцій.

Робота з програмним засобом GRAN-1

Ви всі маєте на столах інструкцію щодо роботи з програмним продуктом GRAN 1

Далі учні працюють за інструкцією.  

Інструкція щодо роботи у програмі GRAN-1 (на екран)

1. Запустити з робочого стола програму GRAN 1;
2. У верхньому рядку екрану знаходиться “головне меню” – перелік “послуг”, до яких можна звернутися в процесі роботи з програмою. Обираємо з меню Об’єкт → Створити.
3. Введи аналітичний вираз функції (за допомогою клавіатури або панелі калькулятора). Справа на панелі обираємо колір, яким буде побудовано цей графік функції.
4. Побудуй графік, звернувшись до послуги Графік→Побудувати;
5. Розкрий вікно «Визначення масштабу», для чого звернися до послуги «Встановити масштаб» в пункті «Опції» головного меню і далі вибери вказівку «Масштаб користувача».
6. Задай проміжки значень для х та у. Наприклад: minХ = - 5, maх Х = 5
7. Щоб витерти усі графіки, звернися меню «Графік» до послуги «Витерти»
8. Щоб зберегти цей файл. На панелі «Меню» обираємо Фал → Записати як → Робочий стол

Робота за інструкцією

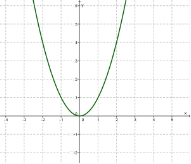
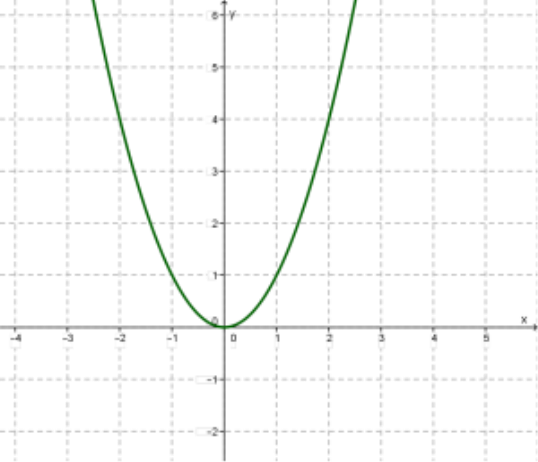
 1) Побудуємо графік функції (y=x^2) - червоний

  2) Побудуємо графік функції +3 - жовтий

 3) Побудуємо графік функції  у=(х-4)²  - синій

 4) Побудуємо графік функції  у= - х² +4  - фіолетовий

          5) Побудуємо графік функції  у= (х – 2)² -3   - зелений

 

На скільки цінними для вас є вміння, набуті під час використання GRAN-1?.....

- Так, дійсно, ви ще раз переконалися, що  комп’ютер полегшує нашу роботу (наскільки швидше ви справилися з цим самим завданням , використовуючи комп’ютер), але повністю виключити математику ми не можемо і не маємо право,  ще Ломоносов сказав «Математику тільки тому потрібно вивчати, що вона розум до ладу приводить».

 

VІ. Підсумок уроку

Самооцінювання 

Діти, ми сьогодні з вами виконували підйом по сходинках знань.

Давайте підведемо  підсумок нашої роботи. На якому етапі зараз кожний з вас?

 

Ми бачимо, що найбільше жовтого кольору.

           Жовтий колір – це колір осені.

           Жовтий колір – це не тільки колір гарних знань.

           Жовтий колір – це колір сонця, віри та оптимізму.

Тому хочу подя­кувати вам за урок, ще раз поба­жати успіху і сказати, що я вірю у ваш успіх!

На згадку про наш урок я хочу поділитися з вами ще од­ним рецептом успіху: «Успіх — це тільки 10 % таланту і 90 % щоден­ної наполегливої праці».

VІІ. Домашнє завдання

Протя­гом уроку ми весь час працювали з партнерами, отримували допомогу один від одного, а в житті дуже часто треба розраховувати тільки на свої сили. І цьому теж потрібно вчитися. Це одна з причин вико­нання домашніх завдань.

Повторити §2, п. 9,10;   № 9.12(2); 9.14(2); 10.11(3,5)

*Зробити фотоколаж

• «Функції в природі»
• «Функції в архітектурі»
• «Функції в техниці»

 

БЛОГ (АНКЕТА)

      «Дорогу осилить той, хто йде»

 

 

 

 

 

 

 

 

 

 

 

 

 

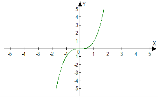
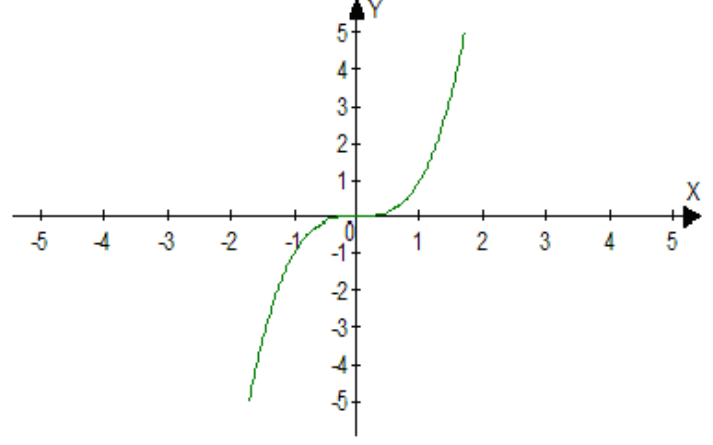
у = х³	кУбічна парабола
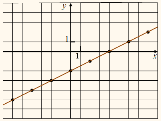
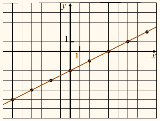
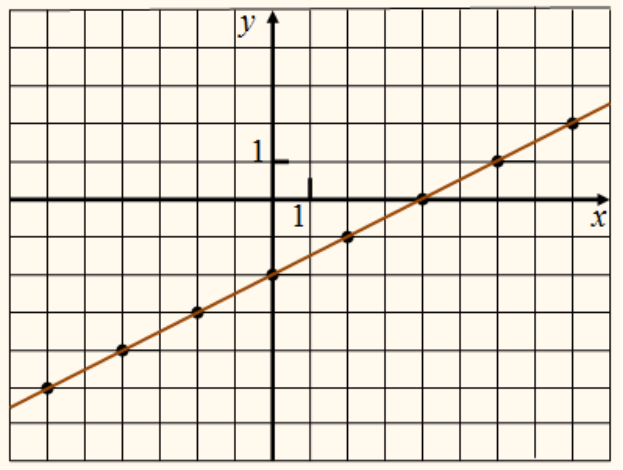
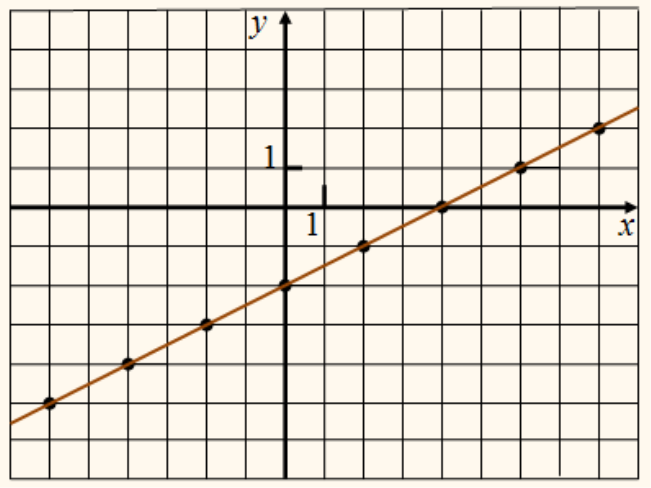
у = kx + b	пряМа лінія
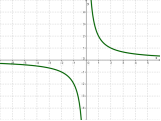
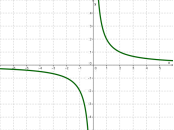
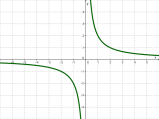
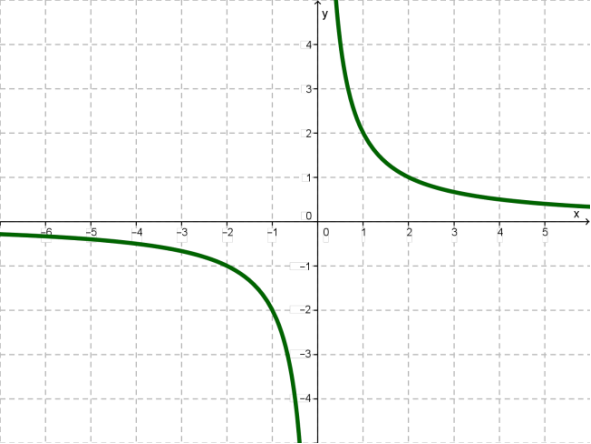
у = 1/х	гІпербола
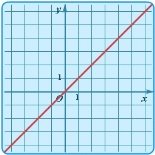
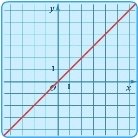
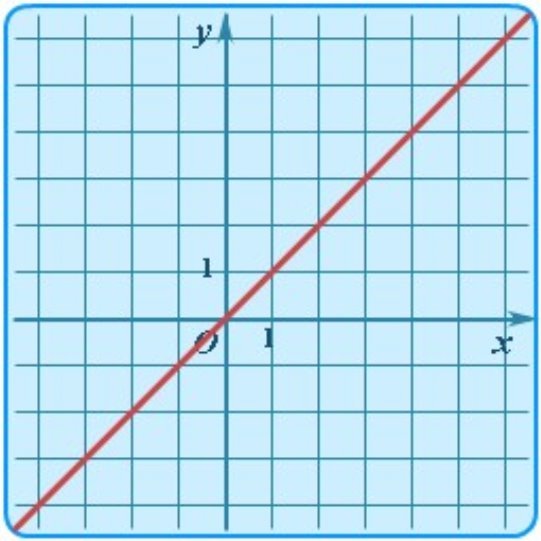
у = kx	пряма, що проходить через початок коордиНат
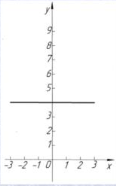
у = b	пряма, паралельНа осі ОХ
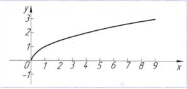
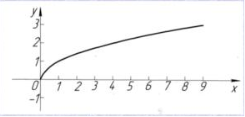
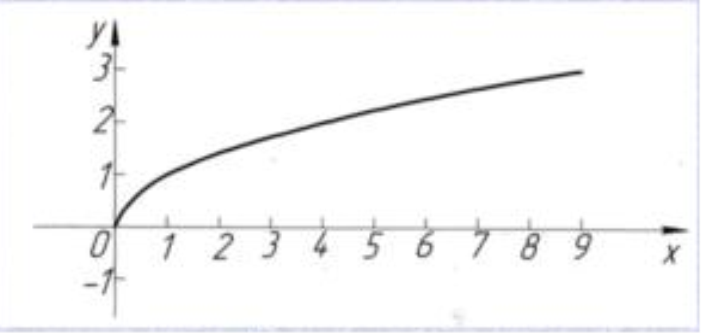
у =	вітка параболи, Яка лежить в першій чверті

 

 

 

у = х³
у = kx + b
у = 1/х
у = kx
у = b
у =

 

 

 

         

          

         

          

         

          

    

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                                                                                                                           

    

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

    

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

     

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

    

 

 

Інструкція щодо роботи у програмі GRAN-1

1. Запустити з робочого стола програму GRAN 1;
2.  У верхньому рядку екрану знаходиться “головне меню” – перелік “послуг”, до яких можна звернутися в процесі роботи з програмою. Обираємо з меню Об’єкт → Створити.
3. Введи аналітичний вираз функції (за допомогою клавіатури або панелі калькулятора). Справа на панелі обираємо колір, яким буде побудовано цей графік функції.
4. Побудуй графік, звернувшись до послуги Графік→Побудувати;
5. Розкрий вікно «Визначення масштабу», для чого звернися до послуги «Встановити масштаб» в пункті «Опції» головного меню і далі вибери вказівку «Масштаб користувача».
6. Задай проміжки значень для х та у. Наприклад: minХ = - 5, maх Х = 5
7. Щоб витерти усі графіки, звернися меню «Графік» до послуги «Витерти»
8. Щоб зберегти цей файл. На панелі «Меню» обираємо Фал → Записати як → Робочий стол

 

Робота за інструкцією

   1) Побудуємо графік функції (y=x^2)

   2) Побудуємо графік функції +3

  3) Побудуємо графік функції  у=(х-4)²

  4) Побудуємо графік функції  у= - х² +4

 5) Побудуємо графік функції  у= (х – 5)² -3

 

 

 

 

 

 

 

 

                  

 

 

          

 

           

 

           

 

 

 

 

 

 

 

 

у = х³	кУбічна парабола
у = kx + b	пряМа лінія
у = 1/х	гІпербола
у = kx	пряма, що проходить через початок коордиНат
у = b	пряма, паралельНа осі ОХ
у = √х	вітка параболи, Яка лежить в першій чверті

 

у = х³	кУбічна парабола
у = kx + b	пряМа лінія
у = 1/х	гІпербола
у = kx	пряма, що проходить через початок коордиНат
у = b	пряма, паралельНа осі ОХ
у = √х	вітка параболи, Яка лежить в першій чверті

 

 

 

 

 

І.Організаційний етап

     -  Вітаю рада новій зустрічі з вами.   Ідучі до вас на урок , згадала одну притчу про філософа Сократа.

      - Одного дня Сократ, оточений учнями, піднімався до храму. Назустріч їм спускався пекар з різною здобою. “Сократ, а чи пишаєшся ти своїми учнями? – запитав пекар. Так. – відповів Сократ. Послухай, варто лише мені задобрити їх здобою, як вони покинуть тебе і підуть зі мною”. На що  мудрець відповів: “Згоден, але ти гукаєш їх вниз, в теплу смачну  долину, а я веду їх вгору, до непереборних, чистих вершин”.

Ось і ми повинні піднятися на сходинки вгору, “долаючи” завдання, які будуть розглянуті на сьогоднішньому уроці,

Зараз ми знаходимося на першій сходинці, але я впевнена, що разом ми зможемо здолати будь-які вершини.  Хочу вам нагадати, що знання  формуюься у нашій уяві тож пропоную вам вправу АК

 

 

 

ІІ. Актуалізація опорних знань

І. Інтерактивна вправа «Асоціативний кущ» https://learningapps.org/watch?v=ppk40chon20

     -  Які поняття асоціюються у вас з терміном  «Функція», а які з темою «Нерівність» (Аргумент, значення функції, область визначення, область значень, способи задання функції: словесний, аналітичний, графічний, табличний; нулі функції, проміжки зростання і спадання функції; числові нерівності; система нерівностей; розв’язок нерівності; числовий проміжок).

 

ІІ. Робота в парах. Гра «Математичне доміно»

  Учням на парти роздаються «доміношки» - картки із функціями, їх назвами і графіками.  Суть гри полягає в тому, щоб виконуючи це завдання вам потрібно скласти відповідність функція        назва        графік та прочитати закодоване слово. Працювати ви будете в групах, допомагаючи один одному.

 

 

 

 

Усе у світі рухається, усе змінюється, нічого не стоїть на місці. Повертається навколо своєї вісі Земна куля, і день змінює ніч, Земля обертається  навколо Сонця, Сонце разом зі всіма своїми планетами вічно прямує у космічні далі. Рослини, дерева ростуть по своїх траєкторіях.

• Здається, до чого тут  функції, і графіки? Саме функція є тим засобом математичної мови, який дозволяє описувати процеси руху, зміни  неповторної краси, що належать природі. Починаючи із XVІІ ст. функція є одним із основних математичних питань. Це поняття і донині відіграє значну роль у розумінні реального світу.

- Отож, сьогодні на уроці ми спробуємо на практиці реалізувати набуті уміння з вивченої теми.

 

 

 

 

Пропоную переглянути ще один ролик.

 (Перегляд відеоролика)???

 Що саме  відображає ролик?

Так, дійсно він відображає графіки функцій, а також функціональні залежності. А ще дозволяє розкрити красу графіків через  створені людиною будівлі, візерунки.

Я згадала слова Костянтина Феофановича Лебединцева, які я хотіла б взяти епіграфом нашого сьогоднішнього уроку.

Епіграф уроку:

                                   Немає жодної галузі людських знань, куди б не    

                                 входило поняття функції та її графічного зображення.

                                                                                                        К.Ф.Лебединцев

 

Тож записуємо число, класна робота та тему нашого уроку   «Найпростіші геометричні перетворення графіків функцій».

 

 

 

 

 

ІV. Узагальнення, систематизація знань.

Тож давайте згадаємо як побудувати графік функції у=f(x) +а за допомогою знайомих вам ресурсів.

ПИСЬМОВО

1. Паралельне перенесення  вздовж осі ОУ на

а одиниць ( якщо а>0, то вгору, якщо а<0, то вниз).

Побудувати графік функції  у=√х +4

Побудувати графік функції у=√х – 3

 

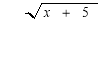2. Паралельне перенесення  вздовж осі ОХ на а одиниць ( якщо а>0, то ліворуч, якщо а<0, то праворуч).

Побудувати графік функції  у=

 

3. Симетрія відносно осі ОХ. у= - √х

    

     4. Побудувати графік функції 

 

 

V. Узагальнення, систематизація  вмінь та навичок.

На сьогодні розроблено значну кількість програмних засобів, що дозволяють розв’язувати досить широке коло математичних задач за допомогою комп’ютерів. Це прикладні програми навчального призначення. Сьогодні на уроці ми скористаємося однією з таких програм, яка дуже спрощує процес побудови графіків функцій.

Робота з програмним засобом GRAN-1

Ви всі маєте на столах інструкцію щодо роботи з програмним продуктом GRAN 1

Далі учні працюють за інструкцією.  

Робота за інструкцією

 1) Побудуємо графік функції (y=x^2) - червоний

  2) Побудуємо графік функції +3 - жовтий

 3) Побудуємо графік функції  у=(х-4)²  - синій

 4) Побудуємо графік функції  у= - х² +4  - фіолетовий

          5) Побудуємо графік функції  у= (х – 2)² -3   - зелений

 

 

На скільки цінними для вас є вміння, набуті під час використання GRAN-1?.....

- Так, дійсно, ви ще раз переконалися, що  комп’ютер полегшує нашу роботу (наскільки швидше ви справилися з цим самим завданням , використовуючи комп’ютер), але повністю виключити математику ми не можемо і не маємо право,  ще Ломоносов сказав «Математику тільки тому потрібно вивчати, що вона розум до ладу приводить».

VІ. Підсумок уроку

Самооцінювання 

Діти, ми сьогодні з вами виконували підйом по сходинках знань.

Давайте підведемо  підсумок нашої роботи. На якому етапі зараз кожний з вас?

 

 

 

Ми бачимо, що найбільше жовтого кольору.

           Жовтий колір – це колір осені.

           Жовтий колір – це не тільки колір гарних знань.

           Жовтий колір – це колір сонця, віри та оптимізму.

Тому хочу подя­кувати вам за урок, ще раз поба­жати успіху і сказати, що я вірю у ваш успіх!

На згадку про наш урок я хочу поділитися з вами ще од­ним рецептом успіху: «Успіх — це тільки 10 % таланту і 90 % щоден­ної наполегливої праці».

VІІ. Домашнє завдання

Протя­гом уроку ми весь час працювали з партнерами, отримували допомогу один від одного, а в житті дуже часто треба розраховувати тільки на свої сили. І цьому теж потрібно вчитися. Це одна з причин вико­нання домашніх завдань.

Повторити §2, п. 9,10;   № 9.12(2); 9.14(2); 10.11(3,5)

*Зробити фотоколаж

• «Функції в природі»
• «Функції в архітектурі»
• «Функції в техниці»

Заповнити форму зворотнього зв’язку за посиланням https://docs.google.com/forms/d/1hxIkn2GKFnnzQpv_3bG4PqHWH0mnXkssvidtVQLaQYE/edit