Найпростіші тригонометричні рівняння
План-конспект уроку з алгебри в 10 класі (рівень стандарту) за новою програмою (за під. О. С. Істер)
Тема уроку: Найпростіші тригонометричні рівняння
Мета уроку: сформувати поняття про найпростіші тригонометричні рівняння, вміння розв’язувати найпростіші тригонометричні рівняння. закріпити основні тригонометричні поняття; розвивати вміння пошукової діяльності, логічне мислення, пам’ять, вміння
аналізувати ситуацію; підвищувати інформаційну культуру, розвивати інтерес до математики;
Форми роботи: індивідуальна, групова.
Тип уроку: засвоєння нових знань, вмінь і навичок.
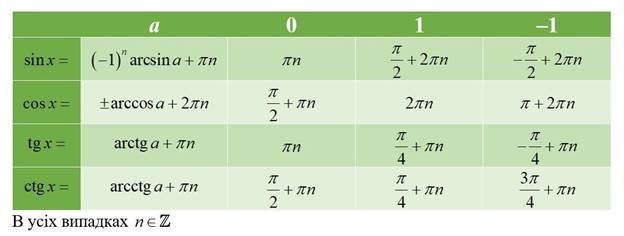
Обладнання: опорний план-конспект, таблиці «Рівняння cos t = a» , «Рівняння sin t = a» , « Рівняння tg t = a», «Рівняння ctg t = a». Хід уроку
І. Організаційний етап
Перевірка готовності учнів до уроку, перевірка відсутніх.
ІІ. Перевірка домашнього завдання
1. Перевірка завдання, заданого за підручником.
Перевірити наявність домашніх завдань в зошитах учнів і відповісти на запитання, які виникли в процесі їх виконання.
ІІІ. Формулювання теми і мети уроку
Краса і багатство тригонометрії – це її формули. Всі вони використовуються при розв’язуванні рівнянь.
Тригонометричні функції застосовуються в науці та техніці, а розв’язання тригонометричних рівнянь є невід’ємною складовою багатьох процесів, які відбуваються навколо нас, тому питання про розв’язування тригонометричних рівнянь досить актуальне . У математиці розглядають рівняння, у яких невідоме (змінна) входить під знак тригонометричних функцій, наприклад:
соs(2х + π/5) = 1; сos2 х/6 - sin2 х/6 = 1 ; cos х = 1, cos х + sin х = 0. Ці рівняння
називаються тригонометричними рівняннями. Як правило, розв'язування будь-якого тригонометричного рівняння зводиться до розв'язування найпростіших рівнянь: sin t = a, cos t = a, tg t = a, ctg t = a.
Отже, сьогодні наше завдання — вивести формули для розв'язування найпростіших тригонометричних рівнянь і навчитися застосовувати їх до розв'язування найпростіших тригонометричних рівнянь.
ІV. Актуалізація опорних знань
На сьогоднішньому уроці ми розглянемо рівняння sin t = a , cos t = a, tgx = t , ctg x = t. З одним із них ви познайомилися дома, коли готувалися до сьогоднішнього уроку. Вам потрібно було розв’язати задачу:
Сторони трикутника дорівнюють 12см і 16см. Знайдіть кут між ними, якщо площа трикутника 48см2.
(Колективне розв’язування задачі)
Розв’язання
![]() ,
,
де а і в – сторони трикутника, α – кут між ними.
Маємо рівняння: ½ ·12·16 ·sin x = 48;
Звідси: 96 sin x = 48,
sinsin x = 12
Синус кута дорівнює ½, коли кут має або 30˚, або 150˚. У розглянутому випадку кути не можуть бути від’ємними або більшими за 180˚. А взагалі
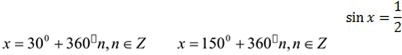
 |
рівняння має безліч розв’язків : та . Але записують розв’язок такого рівняння інакше, давайте визначимо чому? V. Засвоєння знань
Тригонометричне рівняння – рівняння, що містить невідоме під знаком тригонометричної функції.
Рівняння виду sin x = a, cos x = a, tg x = a, ctg x = a називаються найпростішими тригонометричними рівняннями.
1. Рівняння cos x = a
Якщо |a|>1 , то рівняння cosx=a не має коренів.
Наприклад, рівняння cos x = −1,5 не має коренів.
Якщо |a|≤1, то корені рівняння виражаються формулою x = ±arccosa+2πk,kZ
Що ж таке arccos a? Арккосинус в перекладі з латинської означає дуга і ∈ косинус. Це зворотна функція.
Якщо |a|≤1, то arccos a (арккосинус а) - це таке число з відрізка [0;π], косинус якого дорівнює а.
Кажучи інакше: аrccos a = x cos x = a,|a|≤1,x[0;π]
Приклад: ⇒ ![]() ∈
∈
Знайти arccos 2√2
Вираз ![]() показує, що косинус кута x дорівнює
показує, що косинус кута x дорівнює ![]() (cos x
(cos x![]()
Далі просто знаходимо точку цього косинуса на числовому колі, що і є відповіддю:
число, що є значенням осі x, відповідає точці 4π на числовому колі.
Отже, arccos![]()
Зверни увагу!
якщо cos ![]() =
= ![]() , то
, то ![]() =
= ![]()
2. Рівняння sin x = a
Якщо |a|>1, то рівняння sinx=a не має коренів.
Наприклад, рівняння sin x = 2 не має коренів.
Якщо |a|≤1, токорені рівняння виражаються формулою x=(−1)karcsina+πk,kZ
Що ж таке arcsin a? Арксинус в перекладі з латинської означає дуга і синус.∈
Це зворотна функція.
Якщо |a|≤1, то arcsina (арксинус a) - це таке число з відрізка [−π/2;π/2], синус якого дорівнює a. Інакше кажучи:
аrcsina = xsinx=a,|a|≤1,x[−π/2;π/2] Розглянемо цю теорію на прикладі.⇒ ∈
Приклад:
Знайти arcsin 12
Вираз arcsin 12 показує, що синус кута x дорівнює 12 , тобто sinx = 12 . Далі просто знаходимо точку цього синуса на числовому колі, що і є відповіддю:
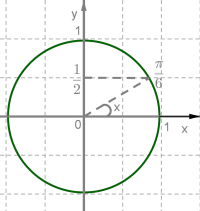
Точка 12 , що знаходиться на осі y, відповідає точці π/6 на числовому колі. Отже, arcsin 12 =π/6
Зверни увагу!
Якщо sinπ/6=1/2, то arcsin1/2=π/6
У першому випадку по точці на числовому колі знаходимо значення синуса, а в другому - навпаки,
за значенням синуса знаходимо точку на числовому
колі. Рух у зворотний бік. Це і є арксинус. Теорема. Для будь-якого a[−1;1] справедлива формула arcsin(−a)=−arcsina
∈
Окремі випадки:
1. sinx=0x=πk,kZ
2. sinx=1⇒x=π/2+2πk,k∈ ∈∈Z
3.sinx=−1⇒⇒x=−π/2+2πk,kZ
3. Рівняння tgx = a
Рівняння tgx = a має розв’язок x = arctga+πk,k∈Z
Що ж таке arctga?
Арктангенс в перекладі з латинської означає дуга і тангенс. Це зворотна функція. arctga (арктангенс a) - це таке число з відрізка (−π2;π2), тангенс якого
дорівнює a.
Інакше кажучи:
arctga=x⇒tgx=a,x∈(−π2;π2)
Теорема. arctg(−a)=−arctga.
4. Рівняння ctgx = a
Рівняння ctgx = a має розв’язок x = arcctga+πk, k∈Z
Що ж таке arcctga?
arcctga (арккотангенс a) - це таке число з відрізка (0;π), котангенс якого
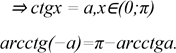 дорівнює a. Інакше кажучи: аrcctga = x
дорівнює a. Інакше кажучи: аrcctga = x
Теорема:
V. Формування вмінь
1. Виконання письмових вправ
Середній рівень
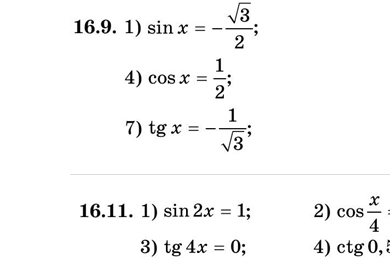
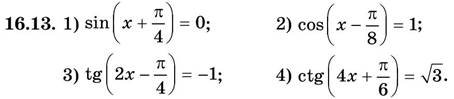
Достатній рівень
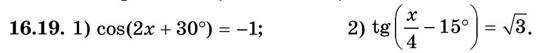
Високий рівень
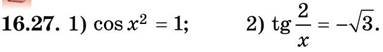
VI. Підсумок уроку
1. Учні відповідають на запитання:
1) Про що ви дізналися на уроці?
2) Під час виконання яких завдань ви відчули труднощі?
2. Рефлексія
Якщо ви не той, хто на вершині, це не значить, що ви той, хто внизу
Учні малюють в зошитах ескіз гори. Позначають своє місцезнаходження до вершини гори, яке відповідає рівню отриманих на уроці знань.
VIІ. Домашнє завдання
Подивитися вдома відео за посиланням https://www.youtube.com/watch?v=nRrAgS-LITQ
Виконати № 16.10 (1, 4, 7), №16. 20
Таблиця 1
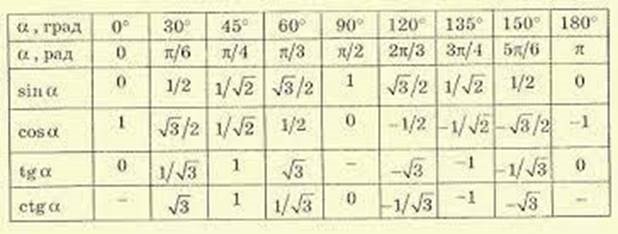
Таблиця 2


про публікацію авторської розробки
Додати розробку
