НЕСТАНДАРТНИЙ  УРОК  МАТЕМАТИКИ

УРОК  -  ГРА  “ОРІЄНТИР”

ГЕОМЕТРІЯ  -  8  КЛАС

ТЕМА.  Декартові координати на площині.

МЕТА.  Закріпити  уміння  і навички застосовувати формули       відстані  між двома точками , формули координат середини відрізка, рівняння прямої та рівняння кола .Розвивати навички знаходити точку  на координатній площині та розв’язувати обернену задачу. Виховувати уважність , відповідальність за колективну справу.

ТИП УРОКУ. Урок узагальнення та систематизації знань.

                                     ХІД  УРОКУ

ВСТУП

1). Історична довідка ( Підготував учень 10-го класу )

     Ідея методу координат з’явилась ще в стародавньому світі. Однією з причин була необхідність орієнтуватись під час плавання у відкритих акваторіях , а не тільки біля берегів . Уже грецький вчений Анаксимандр  ( 610-546 рр до н.е.) чітко описував широту і довготу місця та складав географічні карти з використанням  прямокутних проекцій . Та не тільки потреби мореплавства, а й перехід до осідлого землеробства вимагали розвитку астрономії . І тут для визначення положення  сузір’я і окремих яскравих зірок , планет корисними виявилися координати .Тепер люди так звикли до координат , що іноді просто не помічають , як два числа допомагають правильно і швидко орієнтуватися: квиток до театру містить інформацію про певний ряд і номер місця; залізничний квиток- про номер вагона і номер місця .Широке застосування координати знайшли в будівельній справі , особливо під час монтажних робіт .На заводах працюють координатно-розточувальні верстати.

        Без використання методу координат не могла  б успішно розвиватись космонавтика. На основі складних розрахунків космічний корабель запускають так , щоб він після кількох обертів навколо Землі вийшов в той район космічного простору , в якому в цей момент  на відстані прямого бачення буде космічна автоматична станція , що рухається навколо нашої планети .

      Метод координат міцно увійшов у математику  ( а потім і в інші науки і техніку ) у сімнадцятому столітті. Найбільший вклад в її розробку внесли французькі вчені  Рене Декарт ( 1596-1650 ) та П’єр Ферма (1601-1665) . Книга Декарта  “Геометрія” ( 1637) набула більшого поширення ,ніж  праці Ферма ,  і через це прямокутні координати часто називають декартовими .

         2).Коментар учителя щодо умов проведення  гри : У проведенні уроку допомагають учні 10-го класу. Клас поділено на три рівносильні команди. Лідером команди стає учень який першим виконає правильно 1 завдання. До кожної команди прикріплено 2 учня 10-го класу , які є консультантами та спостерігачами. Лідер команди корегує дії товаришів , а також має право надавати консультації. Кожна консультація зменшує оцінку за дане завдання на 2 бали .

      Кожне завдання учні виконують на окремих листках.

     Якщо учень підняв руку, це означає , що він закінчив виконання завдання. Якщо учень підняв ручку , то він просить допомоги консультанта.

 Перевіряють роботи учитель та асистенти – учні 10-го класу.

Команда одержує на кожному етапі суму балів своїх членів.

1 етап. Учні кожної команди повинні відтворити один із опорних конспектів: 1). Координати  середини відрізка .

                   2).Відстань між точками.

                   3).Рівняння прямої.

Опорні конспекти:

1).  Випадок: АВ не паралельний осі ОY

             А₁С₁ =С₁В₁                                                     у

       x – x₁   =   x – x₂                                                А(х₁;у₁)

x – x₁ =x – x₂ , або  x – x₁ = - (x – x₂ )             А₂

не може бути ,              2 x = x₁ + x₂                 С₂                   С(х;y)

бо  x₁   x₂                                 x = (x₁ + x₂)           В₂                            В(х₂;у₂)

                Аналогічно       y = ( y₁ + y₂ )             0      А₁      С₁     В₁     х

    Якщо АВ паралельний осі ОY , то формули ті ж .

2).   A₁B₁=BC= -  y 

 A₂B₂=AC= -

 A(x₁;y₁)

  AB²=AC²+BC² за т. Піфагора A₂ 

 

                                                                         

 B₂                                              B(x_2;y₂)

AB²=(x₂-x₁)²+(y₂-y₁)²  C

 

 

d² =(x₂-x₁)² + (y₂-y₁)² O       A₁                B₁        x

                         -                                                      

 

                                                      

3).   hA₁A₂ ,   A₁C = A₂C ,                                             A(x;y)

AA₁ = AA₂ , бо ACA₁ = ACA₂       A₁(a₁;b₁)                               

AA₁² = (a₁ – x)² + (b₁ – y )²

AA₂² = (a₂ – x )² + (b₂ – y )²                                  C

                       h            A₂(a₂;b₂)

( a₁ – x  )² + ( b₁- y  )² = (a₂ – x )² + ( b₂ –y )²

2 ( a₂ –a₁)x + 2 (b₂-b₁ )y + (a₁²+b₁²-a₂²-b₂²) = 0

     ax + by +c = 0    -загальне рівняння прямої  h.

 

II етап.  Учням пропонується серія карток : червоного кольору – до 12 балів , синього кольору – до 9 балів , зеленого кольору – до 7 балів. Можливі відповіді записані на дошці у хаотичному порядку .Учитель має відповіді до карток відповідно номерів. Кожен учень вибирає у капітана картку за кольором (за рівнем своїх знань).

 ЧЕРВОНІ  КАРТКИ

1. Довести , що чотирикутник  АВСD , з вершинами у точках  А(-3;1),

B(2;5) , C(3;2) , D(-2;-2) , паралелограм.

2. Довести , що чотирикутник  MNKC – не  є прямокутником , якщо  M(-2;0),   N(3;4) , K(5;2) , C(0;-2).
3. Знайти точку перетину прямих , заданих рівняннями :   x+2y+3-0 , 4x+5y+6=0.
4. Дано три вершини паралелограма  ABCD : A(-2;2) , B(3;3) , C(3;-1) . Знайти  координати точки D.
5. Знайти координати точок перетину двох кіл  x²+y²+2x-2y-2=0  та   x²+y²-2x+2y-2=0
6. Знайти координати точки , яка  лежить на осі ординат і рівновіддалена від двох точок  (1;2)  і  (3;-2) .
7. Знайти точку , рівновіддалену від осей координат і від точки (4;2).
8. Довести , що чотирикутник FEKN з вершинами в точках  F(0;-1),    E(-2;2) , K(1;4) , N(3;1) – квадрат .                                                  ВІДПОВІДІ

1. Координати середини АС : (0; 1,5) ,  середини BD : (0; 1,5).
2. Діагоналі не рівні : МК = 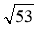, NC = .
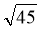3. (1;-2) .
4. D(-2;-2).
5. (1;1) , (-1;-1) .
6. (0;у) = (0;-1) .
7. (x;x) = (10;10) ,або (x;x ) = (2;2) .
8. FE² =EK² = KN² = FN² = 13 ;  FK² = EN² = 26.

                            СИНІ  КАРТКИ

1. Скласти рівняння прямої , що проходить через точки (-2;3) , (3;-2).
2. Довести  , що ABCD –ромб , якщо A(1;1) , B(-2;6)  , C(-5;1) , D(-2;-4) .
3. Доведіть , що  А(1;2) , В(1;6) , С(5;4) – вершини рівнобедреного трикутника.
4. Дано А(5;1) , В(7;2) , С(9;-2) – вершини прямокутного трикутника .
5. Знайти периметр АВС , якщо А(1;1), В(1;7) , С(5;4) .
6. Записати рівняння кола з центром у початку координат , яке проходить через точку М(6;8 ) .                                                         ВІДПОВІДІ

1. y = -x +1.
2. AB² = BC² = CD² = AD² = 29 .
3. АС² = ВС² = 20 .
4. АВ² = 5 , АС² = 25 , ВС² = 20 ;   АС² = АВ² + ВС² .
5. АВ=6; АС=5; ВС=5 ;  Р(АВС) = 6+5+5=16.
6. x² + y² = 100 .

ЗЕЛЕНІ  КАРТКИ

1. Знайти координати середини відрізка АВ , якщо  А(7;8) , В(-2;-3).
2. Знайти  координати центра кола та його радіус , якщо рівняння кола задано у вигляді (х + 2)² + (у – 3 )² = 25.
3. Знайти відстань між точками  А(-12 ; 3 ) і В( -7 ; -9 ).
4. Чи можна побудувати трикутник зі сторонами : а) 2см, 3см , 5см ;     б) 2см , 7см , 6см ;  в)4см , 2см , 1см  і чому ?
5. Знайти діаметр кола заданого рівнянням  х² + (у + 5)² = 49 .
6. Побудуйте на координатній площині  лінію , задану  рівнянням :       2х – у = 0.
7. Побудуйте на координатній площині лінію , задану рівнянням :         (х – 1)² + (у – 2)² = 9.
8. Чи є точка  К(-1; 4 ) серединою відрізка АВ , якщо А(-4; 3) , В(2 ; 7).
9. Знайдіть координати точки перетину діагоналей паралелограма   ABCD , якщо А( 0 ;-3)  , С(1 ; 5 ).
10. Знайти відстань між точками  А(-3; 2) , В( 4 ; 1).

ВІДПОВІДІ                             у                                     

1. (2.5; 2).                                            
2. (-2; 3) , R=5.                                     0      1                   х      

3.  АВ= 13.                                                          

4.  можна у випадку б).                            Рис.1.                  
5.        14.
6. рис.1.
7. коло з центром (1;2) і радіусом =3

8.  ні , бо  (3+7):2 = 5 , а не 4 .

9.  ( 0,5 ; 1).

10..

 

 

ІІІ етап .  естафета      “КОНКУРС   ХУДОЖНИКІВ “

 

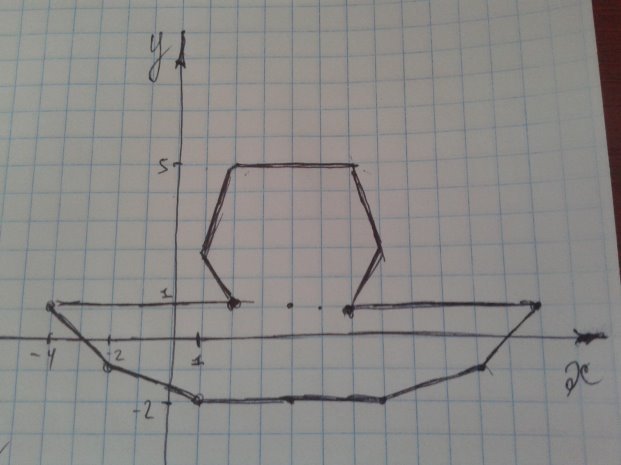
На дошці записано координати точок .Командам видається листок паперу з нанесеною системою прямокутних координат. Кожен член команди ставить одну точку на рисунку і сполучає її з попередньою .У результаті команда одержує рисунок 3. Команда яка першою виконала завдання одержує 10 балів , наступна – 9 балів , остання –8 балів , за кожну неправильно нанесену точку – штраф 1 бал.

 

Точки : (-2;-1) , (-4;1) , (2; 1) , (1;3) , (2;5) , (6;5) , (7;3) , (6;1) , (12;1) , (10;-1) , (7;-2) , (1;-2) , (2;-1).

 

 

 

 

ІY етап .Вікторина  “ ЩАСЛИВИЙ ВИПАДОК”

 

Кожна команда одержує максимум 10 запитань протягом 2-х хвилин. Кожна правильна відповідь приносить команді по 1 балу.

 

1-й конверт

1).  Яка відстань від точки А(3;4) до осі ОХ .     (В:4).

2).  Як називається горизонтальна вісь координат.   (В: Абсцис).

3).  Назвати формули середини відрізка .

                                                      (В: х=(х₁+х₂):2;у=(у₁+у₂):2 ). 

4).  Де знаходиться центр кола  х² + у² =4 . (В: (0;0). )

5). Як розташована пряма  у = х  на координатній площині ?

                    (В: Це бісектриса І та ІІІ  координатних чвертей ) .

6).  Що таке кутовий коефіцієнт прямої ?

                         ( В: Це тангенс кута між прямою та віссю ох ).

7).  Чому дорівнює  Sin 90⁰ ?  ( В: 1) .

8).  Які взаємні розміщення двох кіл на площині ?

(В: Дотикаються, перетинаються у двох точках ,не перетинаються).

9).  В якій чверті знаходиться точка ( -1;2) ?  (В: В  ІІ чверті).

10).Де знаходиться геометричне місце точок площини ХоУ , для яких  

            =5 ?   (В: Це паралельні прямі х=5 та х=-5 ).

2-й конверт

1).  Яка відстань від точки (3;4) до осі оу ? (В: 3).

2).  Як називається вертикальна вісь координат ? (В: Ординат).

3).  Записати формулу рівняння кола. (В: (х-а)²+(у-в)²=r² ).

4).  Як розташована пряма  у=5  на координатній площині ?

   (В: паралельно осі абсцис і проходить через точку (0;5) ),

5).  Ім’ям якого вченого названо прямокутні координати на площині ?

           (В: Рене Декарта ) .

6).  Чому дорівнює  Cos 90⁰ ? (В: нулю).

7).  Чому дорівнює радіус кола    х² + у² = 25 ?  (В: 5).

8).  Які взаємні розміщення прямої і кола ви знаєте ?  (В: Перетинаються у двох точках , дотикаються , не перетинаються ).

9).  В якій чверті знаходиться точка (-2;-3) ? (В: ІІІ чверть ).

10). Де знаходиться геометричне місце точок площини , для яких

       =7 ? (В: Це прямі  у=7 та у=-7 ).

3-й конверт

1).  Яка відстань від точки (3;4) до початку координат ? (В:5).

2).  В якій точці знаходиться початок координат ? (В: (0;0) ).

3).  Записати формулу рівняння прямої на площині. (В:ах+ву+с=0).

4).  Чому дорівнює  Sin 180⁰  ? (В: Нулю ).

5).  Як розташована  пряма  у = -х на площині   ?

         (В: Бісектриса II та IY  координатних чвертей ).

6).  Чому дорівнює радіус кола   х² + у² =100 ? (В: 10).

7).  В якій чверті знаходиться точка  (2;-5) ? (В: В четвертій ).

8).  Як розташована пряма  у = -3 на координатній площині?

      (В: Паралельно осі ох.)

9).  Які особливості розміщення прямої  у = кх +в в залежності від значень  в ? (В: Якщо  b>0 , то пряма  у = кх  піднята вверх на , якщо b<0 , то пряма  у = кх опущенна на вниз .

10). Як називають координати (х ;у) ? (В: Абсциса та ордината ).

Y ПІДСУМОК  ГРИ .

Д/З : Розв’язати  по одній задачі ІІ етапу .