Нетрадиційні методи і прийоми вирішення задач арифметичним способом із використанням моделювання.

Тема 3. Нетрадиційні методи і прийоми вирішення задач арифметичним способом із використанням моделювання.

1. НЕСТАНДАРТНІ ЗАДАЧІ

1.1. Задачі на кмітливість (загадки), задачі-жарти, задачі-головоломки.

Загадки

Загадки розвивають кмітливість, інтригують дітей та стимулюють їхню фантазію. Відгадування загадок розвиває уміння зіставляти, порівнювати предмети та явища, дають багато можливостей для мовного розвитку дітей, прилучення їх до словесної мовної творчості, збагачують уявлення про навколишній світ.

 Не старіє, не вмирає, а все нищить, забирає. (Час)

 Ніг не маю, а ходжу,

Рота не маю, а скажу,

Коли обідати, а коли спати,

Коли роботу починати. (Годинник)

 Що то за гість,

Що темряву їсть? (День)

 Прийшла чорна корова.

Весь світ зборола. (Ніч)

 Чорне сукно лізе у вікно. (Ніч)

 Що було вчора і буде завтра? (День)

 Сіла дівчина спочити

На краю села,

Розчесала довгі коси,

Чорні, мов смола –

В них засяяли Зорини.

Як же звати цю дівчину?

Он підказує нам сич:

Чорні коси чеше …(Ніч)

 Встане – в метр висотою,

Сяде – в метр шириною;

Я уже розгадку дав,

Та ніхто не відгадав. (Метр)

 Дві сестри ідуть-ідуть

І ніколи не зійдуться. (Стрілки годинника)

 Триста шістдесят п’ять чайок,

П’ятдесят два орли,

Дванадцять голубів

Одне яйце знесли. (Дні тижня)

 Три сестри й три брати

З праці йдуть до хати.

Їх сестриця сьома

Зустрічає вдома.

Кличе до світлиці

Їсти паляниці. (Дні тижня)

Задачі- жарти

Це цікаві ігрові задачі з математичним змістом. Для їх розв'язання потрібно більше винахідливості, кмітливості, почуття гумору, ніж вміння виконувати обчислювальні дії (тобто певні знання математики), хоча в більшості з них повністю витримана зовнішня форма арифметичних задач: дано умову, є числові дані й запитання. Побудова, зміст, запитання в цих задачах незвичні. Вони лише побічно нагадують математичну задачу. Суть задачі, тобто ос­новне, завдяки чому можна здогадатися про розв'язок, дати відповідь, замасковано зовнішніми, другорядними умовами. Для правильного їх розв'язання не вимагається виконати арифметичні дії, вони базу­ються на здогадці, кмітливості.  Дітям шкільного віку доступні задачі-жарти як один з видів математичних розваг. Вони є корисним засобом розвитку у дітей логічного мислення, вміння проводити аналіз і синтез, узагальнюва­ти, абстрагувати, порівнювати, зіставляти і конкретизувати, розкри­ваючи зв'язки, що існують між явищами.   Це питання нерозривно пов'язане з розвитком пізнавальних здіб­ностей та інтересів, з певним емоційним ставленням до пізнаваного об'єкту, явища. У процесі роботи над цим видом задач відбувається розвиток правильної, точної, лаконічної математичної мови, а це також одне з важливих завдань формування елементарних математичних уявлень у дітей  шкільного віку.

Завдання:

1. Коли гусак стоїть на двох лапках, його маса 4 кг. Яка маса гусака, якщо він стане на одну лапку? (4 кг)

2. Пара коней пробігла 20 км. Скільки км пробіг один кінь? (20 км)

3. Щоб зварити 1  кілограм м’яса, потрібна 1 година. За який час звариться півкілограма м’яса? (за 1 год)

4. Одна сторона квадрата 5 см, а друга – на 2 см більша. Обчислити площу квадрата.(У квадрата всі сторони рівні)

5. Двоє хлопчиків грали в шахи 1 год 20 хв.  Скільки хвилин грав кожен із суперників? (1 год 20 хв)

6. Ціна книжки 31 грн. Книжка дорожча за обкладинку на 11 грн. Визначити ціну книжки. (31 грн.)

7. Два хлопчики разом йшли до школи і по дорозі знайшли 10 копійок. Скільки грошей знайдуть 4 хлопчики? (10 коп.)

8. Кріль важить 2 кг та ще стільки. Скільки важить його половина? Скільки важить кріль? (2 кг, 4 кг)

9. Який годинник показує точну годину двічі за добу? (Зупинений)

10. Який рік тягнеться один день? (Новий рік)

11. Що буде сороці на сьомому році? (Наступить восьмий)

12. Який годинник не має стрілок? (Сонячний)

13. Термометр показує 15 градусів. Яку  температуру покажуть два таких термометри? (15 градусів)

15. Сашко витрачає на дорогу до школи 10 хвилин. Скільки часу він витратить, якщо піде разом з другом? (10 хв)

Задачі-головоломки

Задачі-головоломки корисні для виховання кмітливості, активізації пізнавальної діяльності учнів. Розв’язуючи їх, діти вчаться критично сприймати умову задачі, ілюструвати її.

1. Маса мішка цукру на 50 кг більша, ніж половина мішка з цукром. Яка маса мішка з цукром? (100 кг)

2. Один насос за одну хвилину викачує 1 т води. За скільки хвилин 5 таких насосів викачають 5 т води? (1хв)

3. Мама з сином їхали в електричці. Мама запитала сина: «В якому по порядку вагоні ми їдемо?» Син відповів: «У шостому. Якщо лічити з голови поїзда або у третьому, якщо лічити з хвоста.» Скільки вагонів у електричці? (8)

4. Довжина однієї сторони шкільного саду дорівнює 32 м. Цю сторону загородили парканом з дошок. Причому кожні 4 м закопували стовп. Скільки всього стовпів знадобилось на паркан? (9 стовпів)

5. Є 5 квадратів зі сторонами по 4 см. З усіх квадратів склеїли прямокутник.

6. Ширина місця склеювання становить 1 см. Яка довжина прямокутника? (16 см)

7. Є два пакети. Один вміщує 300 г цукрового піску, а другий – 650 г. Як за допомогою цих пакетів відсипати 1 кг цукру? (650⋅2 – 300)

8. Батькові 37 років, а сину 12. Скільки років доньці, якщо через 15 років вік доньки й сина дорівнюватиме віку батька? (10 р.)

9. Скільки разів треба розпиляти семиметрову колоду на частини, завдовжки 1 м? (6)

10. У кімнаті є годинник. Він відбиває цілі години. Скільки ударів на добу робить цей годинник? (180 ударів).

11. У двох баках було однакове число літрів води. Коли з першого взяли ¼ води, а з другого 240 л, то в обох баках залишилась однакова кількість води. Скільки літрів води було в баках разом? (1920 л)

12. Як ви гадаєте, за який проміжок часу можна вдвох з’їсти пуд солі? (Приблизно 2 роки, якщо кожен день з’їдати 10 г солі кожному)

13. Сто курей за сто днів з’їдають 100 пудів зерна. Скільки пудів зерна з’їдять 10 курей за 10 днів? (1 пуд)

14. У мішку 100 кг зерна. Як поділити це зерно на дві частини, щоб у одній було на 20 кг більше, ніж у другій? (40 кг і 60 кг)

 

 

1.2. Задачі з логічним навантаженням.

Задачі з логічним навантаженням сприяють розвитку творчих здібностей учнів, готують їх до навчання в старших класах, корисні для використання і на уроках, і під час проведення  математичних змагань, олімпіад, і для організації диференційованої домашньої роботи школярів.

Завдання:

1. Дідові 64 роки, його синові 40 років, а онукові – 12. Через скільки років вік діда дорівнюватиме сумі років сина й онука? (через 12 років)

2. Периметр земельної ділянки прямокутної форми дорівнює 900м, а ширина її на 44 м менша, ніж довжина. Знайти ширину і довжину ділянки. (203 м, 247 м)

3. Є 50 монет по 10 к. і 25 к. загальною вартістю 9 грн 50 к. Скільки окремо монет по 10 к. і 25 к.? (20м, 30м)

4. Сергій на запитання, скільки йому років, відповів, що йому разом з Петриком тепер 36 років, а 6 років тому він був старший за Петрика утричі. Скільки років Сергієві тепер? (24 р.)

5. Батькові 46 років, а синові – 10. Через скільки років батько буде втричі старший за сина? (через 8 років)

6. Галині і Олені разом 26 років, а 3 роки тому Олена була старша від Галини в 4 рази. Скільки років Галині тепер? (19 р.)

7. Марії і Олені разом 16 років, а через 4 роки Олена буде втричі старша за Марію. Скільки років кожній дівчині тепер? (2р., 14 р.)

8. Дідусеві 53 роки, а онукові – 3. Через скільки років дідусь буде в 6 разів старший за онука? (через 7 років)

9. Будівельна бригада витратила крейди у три рази більше, ніж алебастру, але на 23 т менше, ніж цементу, витрата якого була в 3 рази менша від витрати вапна. Знайти витрати кожного з цих матеріалів, якщо всього їх використано 812 т. (135 т, 45 т, 158 т, 474 т)

10. Відстань у 1220 км турист долав по черзі автомобілем протягом 6 год, далі поїздом – 15 год і пароплавом – 7 год. Швидкість автомобіля у 2 рази  більша, ніж швидкість поїзда і у 4 рази більша, ніж швидкість пароплава. Знайти шлях, який подолав турист на кожному виді транспорту. (480 км, 600 км, 140 км).

 

2. ЦІКАВІ ЗАДАЧІ ПІДВИЩЕНОГО РІВНЯ СКЛАДНОСТІ

2.1. Задачі підвищеного рівня складності.

Для того щоб розв’язати складну задачу, треба спочатку намітити план розв’язання. План складають на основі аналізу задач, який проводять від числових даних або від питання задач. Аналізу задачі передує ретельне вивчення умови та питання. Перед тим як розв’язувати задачу треба поставити запитання: про які процеси іде мова в задачі?  Скільки процесів описано в задачі? Якими величинами характеризується процес, описаний в задачі?                                                                                                                                                                                                                                                                    

Задача. Яку загальну суму кредитор повинен покласти в три різні банки, щоб виконувались наступні умови: у банк А потрібно покласти 45% від вкладу в банк В, а сума вкладу в банк становить 80% від вкладу в банк С, а в банк С він вклав суму, яка перевищує вклад в банк А на 6400 гривень?                                                                                                                

Розв'язання

 Нехай х гривень – сума вкладу в банк С. Тоді в банк В потрібно покласти 0,8х гривень, а в банк А – 0,36х гривень. Вклад у банк С перевищує вклад у банк А на (х-0,36х) гривень, що за умовою задачі = 6400 гривень. Отже, в результаті наведених міркувань отримаємо рівняння з однією змінною: х-0,36х=6400, 0,64х=6400, х=10000 (грн), тоді вклад у банк В дорівнює: 0,8⋅10000=8000(грн.) а вклад у банк А: 0,36⋅10000=3600 (грн); загальна сума, вкладена кредитором у банки: 3600+8000+10000.

Відповідь: 21600 грн

Завдання:

1. Клоун сказав, що кількість кошенят, які мешкають у нього дорівнює їх кількості і ще кошеняти. Слова « кошеняти» викликали сміх. Проте клоун сказав правду. Скільки кошенят мешкає у нього? (3 кошеняти)

2. Андрій і Петрик їдуть у сусідніх вагонах потягу «Киї – Івано-Франківськ». Вагон, в якому їде Андрій, – п’ятий з «голови» потягу, а вагон, в якому їде Петрик, – сьомий з «хвоста». Скільки вагонів у цьому потязі? Відповідь обґрунтуйте. ( або вагонів)

3. Сашко, Борис і Василь збирали гриби. Борис знайшов грибів на 20% більше, ніж Сашко, але на 20% менше, ніж Василь. На скільки відсотків більше грибів знайшов Василь, ніж Сашко? (на 50%)

4. Мандрівник повинен подолати пустелю. Його шлях дорівнює 80 км. За один день він долає 20 км та може нести запас їжи та води на 3 дні, тому він повинен робити проміжні бази, щоб поповнювати в них запаси. За скільки днів він може подолати пустелю? (за 6 днів)                                                                                                                                                         

5. Змішуючи два сорти чаю вартістю 30 грн і 50 грн за 1 кг. Скільки грамів чаю вищого сорту потрібно взяти, щоб одержати 500 г суміші вартістю 3 грн 50 коп за 100 г? (125г)

6. У Василька й Марічки було грошей порівну. Коли Василь купив книгу за

14 грн, а Марічка ляльку за 6 грн., то в дівчини залишилося грошей у 3 рази більше, ніж у хлопця. Скільки грошей було в кожного з них спочатку? (18 грн)

7. В одному ящику було в 7 разів більше апельсинів, ніж у другому. Коли з першого ящика взяли 38 апельсинів, а з другого — 14 апельсинів, то в другому залишилося на 78 апельсинів менше, ніж у першому. Скільки апельсинів було в кожному ящику спочатку? (17 і 119)

8. Щодня Ігор робить ранкову зарядку, пробігаючи за тиждень 12 км. Щосуботи і щонеділі він долає удвічі меншу відстань, ніж будь-якого іншого дня тижня. Яку відстань пробігає Ігор щосереди? (2 км)

9. Два жуки змагаються з бігу на 50 м. Перший жук пробігає 1 м за 5 с, а другий — за 4,6 с. Після подолання кожних 10 м дистанції жуки зупиняються на перепочинок: перший — на 10 с, а другий — на 15 с. Який жук фінішує першим? Чи зміниться відповідь, якщо довжина дистанції буде 100 м; 30 м? (одночасно; так)

 

 

2.2. Загадки-жарти.

Відомий французький математик Блез Паскаль зазначав: «Предмет математики настільки серйозний, що корисно не втрачати нагоди зробити його дещо цікавим». Найпоширенішим видом таких завдань є загадки-жарти, запитання-жарти, у яких за простими істинами криється несподіванка, що перетворює задачу на цілком серйозне запитання, для відповіді на яке потрібна увага, кмітливість, зосередженість. Загадки-жарти можна застосовувати як під час уроків, так і в позакласній роботі, оскільки вони мають універсальний характер з точки зору розумового розвитку дитини. Пропоновані задачі можна віднести до загадок-запитань. Їх розв’язання не потребує від учнів особливої математичної підготовки. Достатніми є наявність елементарних знань з математики та кмітливість, яка завжди притаманна допитливому дитячому розуму.

1. Назвіть двоцифрове число, сума цифр якого дорівнює найменшому натуральному числу.

Відповідь: 10.

2. Один хлопчик зірвав за годину 12,5 кг яблук. Скільки яблук зірвуть за годину 5 хлопчиків?

Відповідь: невідомо.

3. Як у кімнаті слід розставити 2 стільці, щоб біля кожної стіни стояло по 1 стільцю?

Відповідь: стільці слід розставити у протилежні по діагоналі кути кімнати.

4. Як, не користуючись метром, від стрічки довжиною 4 м відрізати  триметрову стрічку?

Відповідь: скласти стрічку вчетверо і відрізати четверту частину.

5. Кожен із п’яти братів має одну сестру. Скільки всього дітей у цій сім’ї?

Відповідь: 6 дітей.

6. У батька є син, який удвічі молодший за нього. Син народився тоді, коли батькові було 24 роки. Скільки нині років сину?

Відповідь: 24 роки.

7. Три хлопчики Миколка, Петрик та Іванко йшли до магазину. По дорозі вони знайшли 50 к. Скільки б грошей знайшов Іванко, якби він йшов

до магазину сам?

Відповідь: 50 к.

8. Які читання чисел першої сотні не змінюється при перевертанні їх запису?

Відповідь: 8, 69, 88.

9. Семеро чекали восьмого 14 хв. Скільки хвилин витратив на чекання кожен?

Відповідь: 14 хв.

10. Два автомобілі проїхали 120 км. Скільки кілометрів проїхав кожний автомобіль?

Відповідь: 120 км.

11. Коли ми, дивлячись на цифру «два», кажемо «десять»?

Відповідь: коли дивимося на годинник і говоримо про хвилини.

12. Дві матері і дві дочки порівну поділили між собою три яблука. Як так вийшло?

Відповідь: це були бабуся, дочка й онука.

13. Тракторист, їдучи в село, зустрів три легкових автомобілі та вантажівку. Скільки машин їхало у село?

Відповідь: одна (трактор).

14. У тварини дві праві і дві ліві ноги, дві ноги попереду і дві ноги позаду. Скільки всього ніг у тварини?

Відповідь: 4.

15. П’ять картоплин варяться 30 хв. Скільки хвилин потрібно для того, щоб зварилася одна картоплина?

Відповідь: 30 хв.

16. П’ятеро рибалок за 5 днів з’їли 5 судаків. За скільки днів 10 рибалок з’їдять 10 судаків?

Відповідь: за 5 днів.

17. Відомо, що 26 жовтня — це четвер. Назвіть дату наступного четверга?

Відповідь: 2 листопада.

18. На столі стоять 5 склянок з молоком. Хлопчик випив одну склянку молока. Порожню склянку він поставив на стіл. Скільки склянок залишилося на столі?

Відповідь: 5 склянок.

19. З Кривого Рога до Дніпропетровська о 12 год дня від’їжджає автобус, а на годину пізніше з Дніпропетровська до Кривого Рога — велосипедист, який їде значно повільніше, ніж автобус. Хто з них під час зустрічі буде ближче до Дніпропетровська?

Відповідь: обидва будуть на однаковій відстані.

 20. Один учень розв’язав задачу за хвилину. За який час розв’яжуть цю задачу 10 учнів?

Відповідь: Невідомо.

21. Який знак слід поставити між цифрами 2 і 3, щоб отримане число було більше ніж 2, але менше ніж 3?

Відповідь: кому.

22. На руках — 10 пальців. Скільки пальців на 10 руках?

Відповідь: 50 пальців.

23. У поштовому відділенні за день прийняли 20 посилок загальною вагою 80,8 кг. Скільки важать 10 посилок?

Відповідь: невідомо, бо посилки, як правило, різної ваги.

24. Як, не виконуючи математичних дій, збільшити число 66 на його половину?

Відповідь: необхідно перевернути запис числа 66 і отримане число 99 більше від числа 66 на 33, тобто на його половину.

25. Їхали два батька і два сини. Скільки всього було чоловіків?

Відповідь: троє (дід, батько, син).

26. У яких двох чисел кількість цифр дорівнює кількості букв, за допомогою яких записані ці числа?

Відповідь: 100 — сто; 1 000 000 — мільйон.

27. Скільки картоплин може «увійти» в один  казан?

Відповідь: жодної, бо картопля не ходить.

28. Скільки буде сорок п’ят і сорок п’ят?

Відповідь: вісімдесят п’ят.

29. Коли одиниця дорівнює трьомстам шістдесяти п’яти, п’ятдесяти двом і дванадцяти?

Відповідь: коли це один рік.

30. Якщо о 12 год ночі йде дощ, чи можна чекати, що через 72 год буде сонячна погода?

Відповідь: ні, бо через 72 год, тобто через три доби, буде ніч.

31. Чи можливо, щоб один та один було одинадцять?

Відповідь: так, якщо одиниці поряд записати.

32. У кошику лежить 5 яблук. Чи можна поділити їх порівну між п’ятьма дівчатами так, щоб одне яблуко залишилося у кошику?

Відповідь: так, одне яблуко слід віддати з кошиком.

33. Скільки кінців у п’яти паличок? А у п’яти з половиною паличок?

Відповідь: у п’яти паличок — 10 кінців, у п’яти з половиною — 12 кінців.

34. Щоб проповзти біговою доріжкою стадіону за годинниковою стрілкою, равлику потрібно півтори години. Коли ж равлик повзе по тій самій

доріжці проти годинникової стрілки, то повне коло він здійснює за 90 хв. Чим пояснити розбіжність результатів?

Відповідь: розбіжності немає: півтори години становлять 90 хв.

35. Чому перукар у Женеві швидше зволіє підстригти двох французів, ніж одного німця?

Відповідь: тому що він заробить вдвічі більше грошей.

36. У трикутнику відрізали три кути. Скільки кутів залишилося?

Відповідь: 6 кутів.

37. Стільниця парти має чотири кути. Якщо один з кутів відпиляти, то скільки стане кутів у стільниці?

Відповідь: 5 кутів.

38. Сума яких трьох натуральних чисел дорівнює їх добутку?

Відповідь: 1, 2, 3, бо 1 + 2 + 3 = 1⋅2⋅3.

39. Чи можливо, що 1,5⋅3,8 = 12,67?

Відповідь: ні.

40. Колесо має 10 спиць. Скільки проміжків між спицями?

Відповідь: 10 проміжків.

41. На дереві сиділо вісімнадцять горобців. Бешкетник Сашко влучив з рогачки в одного і той упав. Скільки залишилося горобців?

Відповідь: один, той, що впав.

42. Зазвичай місяць закінчується 30-им або 31-им

числом. В якому місяці є 28-ме число?

Відповідь: у всіх.

43. За книжку заплатили 60 грн. і ще третину її вартості. Скільки коштує книжка?

Відповідь: 90 грн.

44. Летіли качки: одна попереду, дві позаду; одна позаду і дві попереду; одна між двома і три в ряд. Скільки летіло качок?

Відповідь: летіло три качки, одна за одною.

45. Сидять три коти, проти кожного кота сидить два коти. Скільки всього котів?

Відповідь: 3 коти.

46. Біля будинку ростуть дві липи, дві яблуні, дві вишні. Скільки фруктових дерев росте біля будинку?

Відповідь: 4 дерева.

47. У квартирі було 3 кімнати. З однієї зробили 2 кімнати. Скільки кімнат стало у квартирі?

Відповідь: чотири.

48. Назвіть найбільше трицифрове число, яке записане трьома різними цифрами.

Відповідь: 987.

49. Якою цифрою закінчується добуток усіх натуральних чисел від 1 до 13?

Відповідь: нулем.

50. Скільки буде, якщо від тринадцяти відняти середину?

Відповідь: тридцять: три-на-дцять.

51. Жило триста котів і один чоловік. Скільки було ніг?

Відповідь: 2 ноги, бо у котів — лапи.& Σ η

52. Скільки ком треба поставити у складному реченні, яке складається з чотирьох простих?

Відповідь:  три коми.

53. Як слід позначити на сторонах прямокутника 12 точок, щоб на кожній стороні було 4 точки?

Відповідь: треба позначити вершини прямокутника і по дві точки на сторонах.

54. Як, віднявши від дев’яти половину дев’яти, можна отримати 4?

Відповідь: слід записати число 9 римськими цифрами (ІХ) і, розділивши запис горизонтальною рискою, отримаємо у верхній частині число 4, за-

писане римськими цифрами (ІV).

 55. Як поділити 18 на дві рівні частини, щоб у кожній з них вийшло десять?

Відповідь: розділивши запис числа 18 горизонтальною рискою, отримаємо дві десятки.

 

2.3. Задачі на кмітливість. Принцип Діріхле.

При розв’язуванні багатьох задач люди користуються способами міркувань, які одержали назву «принцип Діріхле» («принцип висунутих ящиків»). У найпростішій і дотепній формі принцип Діріхле звучить так: »Не можна посадити 7 зайців у 3 клітки так, щоб у кожній клітці було небільше, ніж 2 зайці». А взагалі твердження формулюється так:

У п клітках неможливо розсадити п + 1 зайців щоб кожний із них сидів у окремій клітці, тобто знайдеться клітка, де сидить не менше двох зайців.

  Щоб застосувати принцип Діріхле до розв'язування задачі, ми повинні вказати, що саме будемо розуміти під «клітками» і «зайцями», а також спосіб, за яким будемо розсаджувати «зайців» у «клітки».

Як правило, під час розв'язування задач використовують не принцип Діріхле, а деяке його узагальнення:

Дано п кліток і пк+1 зайців, які розміщено у ці клітки. Тоді знайдеться клітка, де сидить не менше к + 1 зайців.

Проілюструємо застосування принципу Діріхле на розв’язуванні задач, серед яких є арифметичні й геометричні, жартівливі й побутові. Учням цікаво в них вибирати щоразу «зайців» і будувати для них відповідні «клітки».

Завдання даного типу дуже корисні для розвитку розмовної математичної культури, чіткого розуміння того, що означає розв’язати задачу.

Задача. У класі навчається 29 учнів. Сашко Петренко зробив у диктанті 1З помилок, і ніхто інший не зробив більшої кількості помилок. Довести, що принаймні три учні зробили однакову кількість по­милок.

Розв'язання

Приймемо за «клітки» всі можливі варіанти кількості помилок. їх 14, оскільки учні можуть зробити 0, 1,..., 13 помилок. «Зайцями» вважатимемо учнів, які писали диктант і яких за умовою 29. Кожного з них «садимо» у «клітку», що відповідає кількості зроблених помилок. Зрозуміло, що знайдеться «клітка», в якій «сидять» принаймні три «зайці», а це й означає, що знайдуться три учні, які зробили однакову кількість помилок.

Завдання:

1. У п'ятих класах школи навчається 160 учнів. Довести, що знайдуться 4 учні, у яких день народження припаде на один і той самий тиждень.

Розв'язання

У році може бути максимум 53 тижні. їх і приймемо за «клітки», а за «зайців» — учнів. Розсаджуватимемо «зайців» у ті «клітки», що відповідають їх дням народження. Оскільки 160: 53 = , то за принципом Діріхле знайдеться «клітка», у якій принаймні 4 «зайці». Це означає, що знайдеться тиждень, на який припаде день народження відразу у чотирьох учнів.

2. У клітинках таблиці розмірами 3x3 розмішено числа -1; 0; 1. Розглянемо вісім сум: суми всіх чисел у кожному рядку, кожному стовпці і на двох діагоналях таблиці. Чи можуть усі ці суми бути різними?                                                                                                            

Розв'язання

Нехай «клітками» будуть усі різні значення сум трьох чисел, кожне з яких набуває значення 0, 1 або -1. Зрозуміло, що таких значень 7. Це -3; -2; - 1; 0; 1; 2; 3. «Зайцями» будуть набори із трьох чисел, що розмішені або в одному стовпці, або в одному рядку, або на одній із двох діагоналей таблиці. Таких наборів 8. Як розсаджуватимемо «зайців»? Кожного «зайця» садитимемо в «клітку», що є значенням суми чисел «зайця». Тоді за принципом Діріхле знайдеться «клітка», де сидять не менше двох «зайців». А це й означає, що знайдуться дві розглядувані трійки чисел, для яких суми рівні.

Відповідь: ні.

3. У ящику лежать 10 пар чорних рукавичок і 10 пар червоних одного розміру. Скільки рукавичок потрібно витягнути з ящика навмання, щоб серед них були:

а)  хоча б дві рукавички одного кольору;

б)  хоча б одна пара рукавичок одного кольору?                                                                     

Розв'язання

а)  якщо за «клітки» прийняти кольори рукавичок, то взявши три довільні рукавички, ми отримаємо, що в одній із «кліток» знаходяться два «зайці»-рукавички. А це і вимагається в задачі.

б) якщо взяти 20 рукавичок на одну руку, то з них не можна буде вибрати пару рукавичок одного кольору, тому шукана кількість рукавичок не менша ніж 21. Справді, якщо за «клітки» прийняти кольори рукавичок (їх два), а за «зайців» — рукавички, то за узагальненим принципом Діріхле в одній з «кліток» буде не менше 11 «зайців». Це означає, що знайдеться 11 рукавичок одного кольору. Але ми маємо лише 10 пар рукавичок одного кольору. Тому всі вони не можуть бути на одну руку. Отже, серед цих 11 рукавичок знайдеться одна пара рукавичок одного кольору.

Розглянемо, як принцип Діріхле використовується до розв'язування задач на подільність. Такі задачі — класичний приклад застосування принципу Діріхле.

Завдання:

1. Довести, що серед довільних трьох цілих чисел можна знайти два, сума яких ділиться на 2.

Розв'язання

Приймемо за «клітки» різні остачі від ділення чисел на 2. Їх усього дві:

0 і 1. «Зайцями» будемо вважати остачі від ділення на 2 трьох даних чисел. їх буде три. Розмістивши «зайців» у «клітки» (кожного «зайця» розміщаємо у «клітку», що дорівнює остачі від ділення його на 2), за принципом Діріхле отримаємо, що знайдеться «клітка» з двома «зайцями», тобто знайдуться два числа, що дають при діленні на 2 однакові остачі. їх сума і ділиться на 2.

2. Довести, що серед довільних семи чисел можна знайти три, сума яких ділиться на

Розв'язання

За «клітки» приймаємо різні остачі від ділення на 3. Їх усього три: 0, 1, 2. «Зайцями» вважатимемо остачі від ділення на 3 даних семи чисел. Їх усього 7. Як і в попередній задачі, розмістивши «зайців» у «клітки» і використовуючи узагальнений принцип Діріхле, робимо висновок, що знайдуться три «зайці», що знаходяться в одній із «кліток». А це й означає, що знайдуться три числа, які дають одна­кові остачі від ділення на 3. Їх сума ділиться на 3.

3. Дано 12 довільних цілих чисел. Довести, що з них можна вибрати два, різниця яких ділиться на 11. 

Розв'язання

Приймемо за «клітки» різні остачі від ділення чисел на 11. Їх усього 11. За «зайців» приймемо остачі від ділення даних чисел на 11. Їх усього 12. Розміщуючи «зайців» у «клітки» аналогічно до попередніх задач, за принципом Діріхле отримаємо, що знайдеться два «зайці» в одній із «кліток». А це означає, що знайдеться два числа, які дають однакові остачі від ділення на 11. Зрозуміло, що різниця цих чисел буде ділитися на 11.

Принцип Діріхле використовується і під час розв'язування задач на зафарбовування.

4. Кожну грань куба зафарбовано у білий або чорний колір. Довести, що знайдуться однаково зафарбовані грані, що мають спільне ребро.                                      

Розв'язання

Розглянемо довільну вершину куба. У ній перетинаються три грані. Приймемо за «клітки» кольори, а за «зайців» — грані, що перетинаються в одній вершині. Їх усього три. Тому за принципом Діріхле знайдеться клітка, у якій міститься два «зайці». А це означає, що знайдуться дві грані, які мають спільне ребро (оскільки вони мають спільну точку) і зафарбовані однаково.

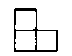5. На шаховій дошці розмірами 8x8 клітинок розставлено 31 фігуру. Довести, що знайдеться вільна фігура, яка складається з трьох клітинок і зображена на малюнку. (див. рис.)

Розв'язання

Для того щоб не було вільної фігури, складеної з трьох клітинок, у будь-якому квадраті розмірами 2х2 клітинки має розміститися не менше двох фігур. Оскільки можна покрити всю дошку 16-ма квадратиками розмірами 2x2 клітинки, що не перекриваються, то всього фігур має бути не менше 32, а у нас є 31. Отже, за сформульованим принципом знайдеться квадрат розмірами 2x2 клітинки, в якому опиниться лише одна фігура. У ній і міститься вільна фігура, що складається з трьох клітинок.

 

2.4. Симетрична стратегія в ігрових задачах.

Діти люблять гратися! Тому в школярів середніх класів великий інтерес викликають задачі-ігри. З їх допомогою можна внести в заняття гуртка елемент розваги, що важливо для учнів 6-го класу.

В той же час такі задачі є змістовними. При їх розв’язуванні школярі звичайно мають значні труднощі. Адже необхідно, по-перше, грамотно сформулювати  стратегію, а по-друге, довести, що вона справді веде до виграшу.

Тому завдання-ігри дуже корисні для розвитку розмовної математичної культури, чіткого розуміння того, що означає розв’язати задачу.

Необхідно усвідомити, що міркування типу “якщо він ходить так, то я ходжу так” не є, як правило, розв’язком гри.

В математичних іграх припускається, що грають двоє гравців, ходи роблять по черзі (жоден із гравців не може пропустити хід), причому гравці не роблять помилок. А тому в таких іграх   наперед можна визначити кінцевий результат, тобто передбачити, який з гравців може забезпечити собі виграш. В цих задачах треба відшукати виграшну стратегію для одного із гравців.

Розглянемо приклади найпростіших задач, де у виграшних стратегіях гравець має робити ходи симетричні у певному сенсі ходам суперника. В наведених прикладах симетричні ходи гарантують гравцеві, що йому буде куди зробити хід. А якщо гра завершується за скінчену кількість ходів, то колись не буде куди походити іншому учаснику.

При виборі симетричної стратегії потрібно пам’ятати таке правило: уперник не повинен мати можливості  перешкодити вашому черговому симетричному ходу.

Задача. Двоє гравців по черзі розламують шоколадну плитку 6 х 8. За один хід дозволяється зробити прямолінійний розлом будь-якого зі шматків уздовж заглиблення на плитці. Програє той, хто не зможе зробити наступного ходу. У котрого з гравців є виграшна стратегія?

Розв'язання

Перемога першого гравця досягається незалежно від його гри, все ж можна було б за­пропонувати для нього цілком ос­мислену стратегію. Припустимо, що своїм першим ходом він розла­мав плитку на дві однакові части­ни розмірами 6х4. Тоді, яку б із цих частин не розламав другий гравець, у першого є можливість зробити аналогічний (симетрич­ний) розлом у тотожній їй другій частині. При цьому одержимо дві пари рівних між собою шматків. Тоді, який би шматок не розламав другий гравець, перший знову має змогу зробити аналогічний розлом шматка, який входить із розлама­ним в ту ж саму пару. Таким чи­ном, скільки б не продовжувалася гра, ходи першого гравця не змо­жуть вичерпатися раніше, ніж хо­ди другого. А оскільки число роз­ломів плитки є скінченним, ми дістаємо, що врешті-решт вичер­паються ходи обох гравців. З попе­редніх міркувань випливає, що ос­танній хід при цьому буде за почи­наючим гру, який і здобуде перемогу.

Завдання:

1. Двоє гравців по черзі кладуть однакові монети на круглий стіл, причому так, щоб вони не накладалися одна на одну. Програє той, хто не може зробити хід.

Розв’язання

В цій грі виграє перший гравець, незалежно від розмірів столу. Першим ходом він кладе монету так, щоб центри монети і столу співпали. Після цього на кожний хід другого гравця перший гравець відповідає симетрично щодо центру столу. При такій стратегії після кожного ходу першого гравця позиція симетрична. Тому, якщо черговий хід другого гравця можливий, то можливий і симетричний йому відповідний хід першого гравця. Отже, перший гравець перемагає.

2. Двоє гравців по черзі ставлять слонів на клітинки шахової дошки так, що слони не б’ють один одного (колір слонів значення не має). Програє той, хто не може зробити хід.

Розв’язання

Шахова дошка симетрична відносно свого центра, тому, на перший погляд, другий гравець на кожен хід першого має симетричний хід. Однак це не так, бо, якщо перший гравець ставить слона на одну з клітинок головної діагоналі, то другий гравець симетричного ходу немає. Щоб розв’язати задачу за допомогою симетричної стратегії, необхідно знайти симетрію, при якій попередній хід суперника не перешкоджає дотриманню обраної стратегії. Такою є симетрія відносно прямої, що розділяє четверту і п’яту горизонталі. Симетричні відносно неї поля мають різний колір, і тому слони, поставлені на такі поля, не б’ють один одного.

Отже, другий гравець виграє, якщо на кожен хід першого гравця відповідає ходом, симетричним відносно вказаної прямої.

3. Хлопчик та дівчинка по черзі зафарбовують клітинки прямокутної таблиці. За один хід треба зафарбувати дві не зафарбовані клітинки, які мають спільну сторону. Починає гру дівчинка, а програє той, хто немає можливості зробити хід. Хто переможе при правильній грі, якщо таблиця має розміри:      

 а) 2004 х 2006;   б) 2005 х 2006?

Розв’язання

а) переможе хлопчик. Після кожного ходу дівчинки йому треба зафарбувати ту пару клітинок, яка центрально – симетрична відносно центра прямокутника клітинкам, тільки що зафарбованими дівчинкою. Простіше кажучи, ходи хлопчика повинні бути центрально – симетричні ходам дівчинки. Клітинки для такого ходу хлопчика завжди будуть чистими. Адже після кожного ходу хлопчика набір не зафарбованих клітинок буде мати центр симетрії – центр прямокутника. І якщо дівчинка обере для свого ходу якісь дві чисті клітинки, то чистими будуть і клітинки для ходу хлопчика. Оскільки загальна кількість клітинок скінченна, гра колись кінчиться, а програти може лише дівчинка. Для стратегії хлопчика важливим буде те, що центр прямокутника лежить у вершині клітинки.

б) виграє дівчинка. Для прямокутника 2005 х 2006 центр симетрії лежить всередині спільної сторони двох клітинок, і першим ходом дівчинці треба зафарбувати ці дві клітинки. Далі вона повинна робити ходи, центрально – симетричні ходам хлопчика відносно центра прямокутника.

4. Прямокутна шоколадка розділена 4 повздовжніми та 9 поперечними заглибленнями на 5х10=50 квадратних частин. Перший гравець розламує шоколадку по деякому заглибленню на дві прямокутні частини. Два гравці по черзі одну із отриманих частин по заглибленнях ділять на дві прямокутні частини. Хто виграє при правильній грі, якщо той, хто відламає частку 1х1:  а) програє; б) виграє.

Розв’язання

В обох випадках виграє перший гравець, і першим своїм ходом він має розламати шоколадку на дві частини 5х5.

а) на кожний хід другого гравця на одній половині шоколадки першому треба зробити такий же хід на іншій. Очевидно, що частку 1х1 раніше отримає другий гравець.

б) перший гравець дублює ходи другого в іншій половині шоколадки, поки другий не відламає якусь частку 1х п. Тоді з цієї частини перший отримує частку 1х1.

5. Дано смужку розміром 1х 2005. Двоє учнів грають у гру, по черзі роблячи свої ходи. За один хід потрібно закреслити одну довільну клітинку смужки або деякі дві послідовні клітинки. Програє той, хто не зможе зробити хід. Хто може забезпечити собі виграш – перший гравець чи його суперник?

Розв’язання

Перемогу може забезпечити собі перший гравець. Першим ходом він закреслює 1003-тю (центральну) клітинку, а потім повторює ходи суперника симетрично відносно неї.

6. Двоє гравців по черзі кладуть п’ятикопійчані монети на прямокутний стіл. Монети повинні повністю вміщуватися на столі і не торкатися одна одної. Той, кому нікуди покласти монету, програє. Хто переможе при правильній грі – той, що ходить першим чи той, хто другим? (виграє той, хто ходить першим. Йому треба першу монету покласти в центр стола, а потім класти монети симетрично ходам другого відносно центра стола)

7. На колі розставлено 20 точок. За хід дозволяється сполучити будь-які дві з них відрізком, що не перетинає відрізків, які проведено раніше. Програє той, хто не може зробити хід. Хто переможе при правильній грі – той, що ходить першим чи той, хто другим? (виграє перший гравець. Перший хід – провести хорду, по обидва боки від якої розміщено по 9 точок. Виграшна стратегія – симетричні ходи)                                        

8. Двоє гравців по черзі ставлять коней на клітинки шахової дошки так, що коні не б’ють один одного. Програє той, хто не може зробити хід. Хто переможе при правильній грі – той, що ходить першим чи той, хто другим? (виграє другий гравець. Виграшна стратегія – центральна або осьова симетрія)

9. Двоє гравців грають в шашки на дошці 8 х 8. При цьому забороняється бити шашки суперника та перетворювати шашки в дамки. Програє той, хто не може зробити хід. Хто переможе при правильній грі? (виграє другий гравець. Йому треба робити ходи, симетричні ходам партнера, відносно центра дошки)

Завдання:

1. Два гравці записують по черзі числа 1 і –1 в одиничні клітинки таблиці розміром 1987 х 1987. Після того, як всі клітинки заповнені, для кожного рядка, стовпця і двох діагоналей таблиці підраховується добуток чисел, які там записані. Довести, що гравець, який робить перший хід, може грати так, щоб серед цих добутків було рівно 1990 додатних.

Розв’язання

Оскільки число 1987 непарне, то існує клітинка, центром якої є центр симетрії даної таблиці. Для кожної іншої клітинки існує клітинка, симетрична з нею відносно центра таблиці. Якщо перший гравець хоче домогтись вказаного в задачі результату, то своїм першим ходом він має записати в центральну клітинку число (-1), а після кожного ходу другого гравця йому слід записувати число протилежного знаку в клітинку, симетричну відносно центра таблиці із клітинкою “суперника”. Якщо, наприклад, другий гравець своїм першим ходом записує число (+1) в клітинку першого стовпця, то перший гравець записує число (-1) в симетричну з нею клітинку 1987-го стовпця. Після цього обміну ходів в кожному із заданих стовпців залишиться по 1986 клітинок, тому в першому стовпцеві буде 993+1 число (+1) і 993 числа (-1), тобто добуток чисел буде дорівнювати –1. В 1987 стовпцеві буде 994 клітинки з числами (-1) і 993 – з числами (+1). Добуток всіх чисел дорівнює (+1). Таким чином, в тому рядку чи в тій діагоналі, де перший запис робить перший гравець, добуток чисел дорівнює (+1). Сюди відносяться, перш за все, обидві діагоналі, той рядок і той стовпець, які містять центральну клітинку (всього 4). В решті рядків і стовпців буде 1986 з додатними добутками і 1986 – з від’ємними.     1986 + 4  = 1990.

2. У рівностях  *+*+*=*, *+*=*, *=*  двоє вписують по черзі на свій розсуд замість зірочок цілі числа. Довести, що той, хто починає гру, завжди може досягти правильності усіх числових рівностей.

Розв'язання

Перший гравець повинен записати довільне ціле число замість однієї із зірочок другої рівності. Далі, записуючи числа в тій же рівності, що і його суперник, він матиме змогу записати останні числа кожної рівності, а отже, і добитися їх виконання.

Слід зауважити, що відступ від описаної стратегії може привести першого гравця і до поразки. Наприклад, суперник негайно міг би скористатися із вписування числа у третю рівність.

3. Дано шахівницю 8 х 8 і прямокутні доміно 1 х 2. За один хід дозволяється накрити дві сусідні клітинки шахівниці так, щоб плитки доміно не перекривались. Програє той, хто не зможе зробити наступного ходу. У котрого з двох гравців є виграшна стратегія?

Розв'язання

Виграшна стратегія є у другого гравця. Для перемоги він кожного разу повинен ставити плитку доміно симетрично відносно центра дошки до плитки, поставленої перед цим його суперником.

4. Двоє по черзі ставлять на вільні клітинки шахової дошки коней: один – білих, другий – чорних, роблячи це так, щоб виставлений кінь не міг бути взятий  жодним із вже поставлених противником коней. Програє той, хто не може зробити черговий хід. Хто виграє при правильній грі: той хто починає гру чи його партнер – і як треба ходити, щоб виграти?

Розв'язання

Нехай другий гравець, роблячи черговий хід, ставить свого коня на клітинку, яка симетрична відносно центра дошки клітинці, на яку тільки що поставив коня його партнер. Доведемо, що вказана стратегія дозволяє другому гравцю завжди добитися перемоги. Для цього покажемо, що якщо перший гравець може зробити черговий хід, то черговий хід може зробити і його партнер.

В силу вибору стратегії, по-перше, вільна клітинка, на яку другий гравець ставить коня. По-друге, цей кінь не може бути взятий тільки що поставленим конем партнера, бо ці коні знаходяться на клітинках одного кольору. По-третє,  цей кінь не може бути взятим жодним з інших виставлених партнером коней: якби він міг бути взятий з клітинки А, то виставлений останнім кінь першого гравця міг би бути взятий конем із клітинки, симетричної А відносно центра.

Зауваження.  Існують і інші стратегії, які дозволяють завжди виграти тому, хто ходить другим. Наприклад, він може ставити коня на клітинку, симетричну клітинці, на яку тільки що поставив коня його партнер, відносно вертикальної (горизонтальної) осі симетрії дошки.

5. Дано клітчасту дошку 10 х 10. За хід дозволяється покрити будь-які дві сусідні клітинки прямокутником 1 х 2 так, щоб прямокутники не перекривались. Програє той, хто не може зробити хід. (Виграє другий гравець. Центральна симетрія)

6. В кожній клітинці дошки 11 х 11 стоїть шашка. За хід дозволяється зняти з дошки будь – яку кількість шашок, що йдуть підряд, або з одного вертикального, або з одного горизонтального ряду. Виграє той, хто зняв останню шашку. (Виграє перший гравець. Першим  ходом він знімає центральну шашку, а потім грає центрально симетрично)

7. Два гравці по черзі записують числа 1 і –1 в клітинки таблиці розмірами 1993 х 1993. Після того, як всі клітинки заповнені, для кожного рядка, кожного стовпчика і двох діагоналей таблиці підраховується добуток чисел, які там записані. Довести, що гравець, який робить хід першим, може грати так, щоб серед цих добутків було рівно 1996 від’ємних. (Шуканою стратегією є така: перший гравець ставить –1 в центральну клітинку. Якщо другий гравець записує в деяку клітинку певне число, то перший гравець записує протилежне число в клітинку, яка симетрична клітинці другого гравця відносно центральної клітинки)

8. Два гравці по черзі кладуть фішки на клітинки дошки 101 х 101. Перший може покласти чергову фішку на будь-яку вільну клітинку, для якої кількість фішок, які вже стоять в стовпці та рядку, що містять цю клітинку, парна. Другий може покласти чергову фішку на будь-яку вільну клітинку, для якої така кількість непарна. Програє той, хто не може зробити хід. Хто виграє при правильній грі? (Виграє перший гравець. Він першим своїм ходом кладе фішку в центральну клітинку, а потім робить ходи симетрично відносно стовпця, який проходить через центральну клітинку, при умові, що другий гравець перед цим не поставив фішку у цей стовпець. У супротивному разі він (перший гравець) робить ходи симетрично відносно центральної клітинки)

9. Є дошка 50 х 50. Двоє по черзі закреслюють вибрану клітинку, а також клітинки, які знаходяться над нею і справа від неї. Програє той, хто закреслить ліву нижню клітинку. Хто виграє при правильній грі: перший гравець чи його партнер? (Виграє перший гравець. Першим своїм ходом він повинен закреслити квадрат 49 х 49, а потім ходити симетрично)

 

 

 

 

 

 

 

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

1. Бантова М.О. Методика викладання математики в середніх класах - К.: Вища школа. Головне видавництво, 1982. – 14-21с.-Укр.

2. Богданович М.В., Козак М.В., Король Я.А. Методика викладання математики в середніх класах: Навч. пос. – 3-є вид., перероб. і доп. – Тернопіль: Навчальна книга – Богдан, 2008. – 336с.

3. Математика: підруч. для 5 кл. загальноосв. навч. закл. / М.В. Богданович, Г.П. Лишенко. – К.: Генеза, 2012. – С. 260-276.

4. Математика: підруч. для 5 кл. загальноосвіт. навч. закл. / Ф.М. Рівкінд, Л.В. Оляницька. – К.: Видавничий дім «Освіта», 2012. – 144с.

5. Богданович М.В. Математика: Проб. підруч. для 5 кл. – К.: Освіта, 2001. – 128с.

6. Богданович М.В. Методика викладання математики в середніх класах : Навч. посібник К.: А.С.К., 1999. – 243-283с.: іл.

7. Богданович М.В. Урок математики в середній школі. Посібник для вчителя.-К.: Рад. шк., 1990. – 116-117с.