Незвичайні способи множення чисел

Незвичайні способи множення.

Трохи історії.

Ті способи обчислень,  якими ми користуємося зараз, не завжди були так прості і зручні. У давнину користувалися більш громіздкими і повільними прийомами. І якби школяр 21 століття міг перенестися на п'ять століть тому, він вразив б наших предків швидкістю і безпомилковістю своїх обчислень. Звістка про нього облетіла б навколишні школи і монастирі, затьмаривши славу майстерних лічильників тієї епохи, і з усіх боків приїжджали б навчатися у нового великого майстра.

 Особливо важкі в давнину були дії множення і ділення. Тоді не існувало одного виробленого практикою прийому для кожної дії. Навпаки, в ходу була одночасно мало не дюжина різних способів множення і ділення - прийоми один іншого заплутаніше, запам'ятати які не в силах була людина середніх здібностей. Кожен вчитель рахункового справи тримався свого улюбленого прийому, кожен «магістр поділу» (були такі фахівці) вихваляв власний спосіб виконання цієї дії.

У книзі В. Беллюстин «Як поступово дійшли люди до справжньої арифметики» викладено 27 способів множення, причому автор зауважує: «вельми можливо, що є й ще способи, приховані в тайниках книгосховищ, розкидані в численних, головним чином, рукописних збірках».

 І всі ці прийоми множення - «шаховий», «загинанням», «хрестиком», «гратами», « задом наперед », «алмазом» та інші змагалися один з одним і засвоювалися з великими труднощами.

Давайте розглянемо найбільш цікаві та прості способи множення.

 

 

Найпростіші випадки множення

Множення на «2» і на «4 ».

Множимо на 2, починаючи зі старших розрядів.

Наприклад: 269 * 2 = 200 * 2 +60 * 2 +9 * 2 = 400 +120 +18 = 638

Множення на 4 зводиться до двократного множення на 2.

Наприклад: 75 * 4 = 75 * 2 * 2 = 150 * 2 = 3002 .

 

Множення на 5.

Щоб помножити на 5, потрібно помножити на 10 і результат розділити навпіл.

Наприклад: 74 * 5 = 74 * 10:2 = 74:2 * 10 = 370

 

Множення на 25.

При множенні на 25 ми множимо на 100 і ділимо на 4, або ділимо на 4 і множимо на 100.

Наприклад: 56 * 25 = 56:4 * 100 = 16007 * 25 = 7 * 100:4 = 700:4 = 175

 

Множення на 1,5 на 15.

Дуже легко збільшити число в 1,5 рази для цього потрібно до самого числа додати його половину.

Наприклад: 62 * 1,5 = 62 +31 = 93

Щоб помножити число на 15, ми збільшуємо його в 10 разів і до отриманого числа додаємо половину того, що вийшло.

Наприклад: 68 * 15 = 680 +340 = 10206 .

 

Множення на 9 .

Щоб помножити дане число на 9, потрібно збільшити його в 10 разів і від отриманого результату відняти дане число.

Наприклад: 67 * 9 = 67 * 10-67 = 670-67 = 60335 * 9 = 35 * 10-35 = 350-35 = 3157.

 

Множення на 99.

Неважко здогадатися, як чинити при множенні на 99.

Потрібно, збільшити дане число в 100 разів і від отриманого числа відняти дане число.

Наприклад: 54 * 99 = 54 * 100-54 = 5400-54 = 5346 .

31 * 99 = 31 * 100-31 = 3100-31 = 3069

 

Множення на 101.

Особливо просто множення двозначного числа на 101. Потрібно подумки приписати праворуч до даного числа це ж число і прочитати те, що вийде.

Наприклад: 63 * 101 = 6363

54 * 101 = 54549 .

 

Множення на 11.

Щоб помножити яке-небудь число на 11, потрібно збільшити його в 10 разів і до отриманого результату додати дане число.

Наприклад: 11 * 46 = 46 * 10 +46 = 460 +46 = 504

Інший спосіб множення двозначного числа на 11. Між цифрами двозначного числа вставляємо їх суму. 36 * 11. Між 3 та 6 (3 ... 6 ) вставляємо суму 3 +6 = 9 . Отримаємо 396. Значить, 36 * 11 = 396.10.

 

Зведення в квадрат числа, що закінчується цифрою 5.

Щоб звести в квадрат число, що закінчується цифрою 5 (наприклад: 65 ), множать число десятків (6) на число десятків, збільшене на 1 (на 6+1 = 7), і до отриманого числа приписують 25 (6 * 7 = 42. ) Відповідь: 4225.

 

 

Множення на пальцях.

 

Давньоруський спосіб множення на пальцях є одним з найбільш уживаних методів, яким успішно користувалися протягом багатьох століть російські купці. Вони навчилися множити на пальцях однозначні числа від 6 до 9. При цьому достатньо було володіти початковими навичками пальцевого рахунку "одиницями", "парами", "трійками", "четвірками", "п'ятірками" і "десятками". Пальці рук тут служили допоміжним обчислювальним пристроєм.

Для цього на одній руці витягали стільки пальців, на скільки перший множник перевершує число 5, а на другий робили те ж саме для другого множника. Інші пальці загинали. Потім бралося число (сумарне) витягнутих пальців і множилося на 10, далі перемножував числа, що показували, скільки загнуто пальців на руках, а результати складалися.

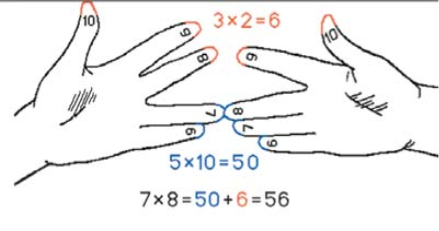Наприклад, помножимо 7 на 8. У розглянутому прикладі буде загнуто 2 і 3 пальці. Якщо скласти кількості загнутих пальців ( 2 +3 = 5) і перемножити кількість не загнутих ( 2 • 3 = 6 ), то вийдуть відповідно числа десятків і одиниць шуканого числа 56. Так можна обчислювати добуток будь-яких однозначних чисел, більше 5.

 

Множення на 9.

 

Множення для числа 9 - 9 • 1, 9 • 2... 9 • 10 - легше вивітрюється з пам'яті і важче перераховується вручну методом складання, однак саме для числа 9 множення легко відтворюється "на пальцях". Розведіть пальці на обох руках і поверніть руки долонями від себе. Подумки присвойте пальцям послідовно числа від 1 до 10, починаючи з мізинця лівої руки і закінчуючи мізинцем правої руки (це зображено на малюнку).

 

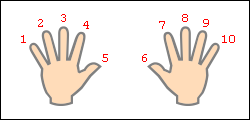
Наприклад,  ми хочемо помножити 9 на 6. Загинаємо палець з номером, рівним числу, на яке ми будемо множити дев'ятку. У нашому прикладі потрібно загнути палець з номером 6. Кількість пальців ліворуч від загнутого пальця показує нам кількість десятків у відповіді, кількість пальців праворуч - кількість одиниць. Зліва у нас 5 пальців, не загнуто, праворуч - 4 пальці. Таким чином, 9 • 6 = 54. Нижче на малюнку детально показано весь принцип " обчислення".

 

 

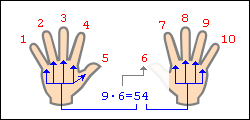
Спробуємо помножити 9 на 7. Для цього Вам треба загнути на першій руці палець з номером 9, а на другий відповідно 7.

Далі починаємо рахувати за наступним правилом: порахуйте скільки пальців у Вас всього до загнутих включно (в нашому випадку їх 6 — на першій руці під номерами 6,7,8,9 і на другій під номерами 6 і 7). Далі кількість цих пальців множимо на 10. У нашому випадку 6х10 = 60, тепер порахуйте кількість пальців, які залишились на кожній руці окремо, в нашому випадку на першій руці 1, на другій 3, перемножимо ці два числа: 1х3 = 3. У висновку складемо свої дві відповіді, тобто 60 і 3 : 60 +3 = 63, значить 9х7 = 63.

 

Тепер помножимо на 7 8:

Кількість пальців, пронумерованих блакитним кольором — 5, множимо 5 на 10, отримуємо 50, кількість пальців, пронумерованих червоним кольором, на першій руці 3, на другій — 2, перемножимо 2 і 3, отримуємо 6. Складаємо отримані відповіді 50 +6 = 56, значить 7х8 = 56.

 

Ось так виглядає операція множення чисел від 6 до 10.

 

 

 

 

 

 

Множення на 9 (легший спосіб).

В останній час все частіше стикаюся з учнями середньої та старшої ланки, які не знають таблицю множення. А знати її треба, зазвичай її просто «зубрять» ще у другому класі. Але математика — це наука «думаючого мозку» і вчити її не обов’язково, адже існує безліч схем і алгоритмів вирішувати швидко, не заучуючи що-небудь.

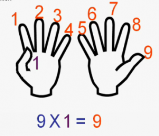Зараз розглянемо як в прямому сенсі відбувається множення на пальцях.

Множення на 9:

9х1 = 9 (при множенні на 1 — загинаємо перший палець, потім рахуємо кількість пальців до загнутого (їх 0) і після нього (їх 9), результат 09 або просто 9)

 

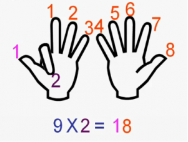9х2 = 18 (при множенні на 2 — загинаємо другий палець, потім рахуємо кількість пальців до загнутого (їх 1) і після нього (їх 8), результат 18)

 

 

 

Ще приклад: потрібно обчислити 9 • 8 = ?. По ходу справи скажемо, що в якості "лічильної машинки" не обов'язково можуть виступати пальці рук. Візьміть, наприклад, 10 клітинок в зошиті. Закреслюємо 8-у клітинку. Зліва залишилося 7 клітинок, справа - 2 клітини. Значить 9 • 8 = 72. Все дуже просто.

 

 

 

 

Індійський спосіб множення.

Найцінніший внесок у скарбницю математичних знань був здійснений в Індії. Індуси запропонували вживаний нами спосіб запису чисел за допомогою десяти знаків: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.

Основа цього способу полягає в ідеї, що одна і та ж цифра позначає одиниці, десятки, сотні або тисячі, залежно від того, яке місце ця цифра займає. Займане місце, у разі відсутності яких - не будь розрядів, визначається нулями, приписуються до цифр.

Індуси відмінно рахували. Вони придумали дуже простий спосіб множення. Вони множення виконували, починаючи зі старшого розряду, і записували неповні добутки саме над множимо, порозрядно. При цьому відразу було видно старший розряд повного добутку  і, крім того, виключався пропуск будь-якої цифри. Знак множення ще не був відомий, тому між множниками вони залишали невелику відстань. Наприклад, помножимо їх способом 537 на 6 :

 

537 6

 

   ( 5 ∙ 6 = 30 ) 30

 

537 6

 

   ( 300 + 3 ∙ 6 = 318 ) 318

 

                                                           537 6

 

   ( 3180 +7 ∙ 6 = 3222 ) 3222

 

 

 Множення способом « МАЛЕНЬКИЙ ЗАМОК».

Множення чисел зараз вивчають у першому класі школи. А от у Середні століття зовсім небагато володіли мистецтвом множення. Рідкісний аристократ міг похвалитися знанням таблиці множення, навіть якщо він закінчив європейський університет.

За тисячоліття розвитку математики було придумано безліч способів множення чисел. Італійський математик Лука Пачолі у своєму трактаті «Сума знань з арифметики, відношеннях і пропорційності» (1494) наводить вісім різних методів множення. Перший з них носить назву «Маленький замок», а другий не менш романтичну назву «Ревнощі або решітчасте множення».

Перевага способу множення «Маленький замок» в тому, що вже з самого початку визначаються цифри старших розрядів, а це буває важливо, якщо потрібно швидко оцінити величину.

Цифри верхнього числа, починаючи зі старшого розряду, по черзі множаться на нижнє число і записуються в стовпчик з додаванням потрібної кількості нулів. Потім результати додаються.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Множення чисел методом «ревнощі».

Другий спосіб носить романтичну назву «ревнощі», або «решітчасте множення».

Спочатку малюється прямокутник, розділений на квадрати, причому розміри сторін прямокутника відповідають числу десяткових знаків у множимо і множника. Потім квадратні клітини, діляться по діагоналі, і «... виходить картинка, схожа на ґратчасті віконниці - жалюзі, - пише Пачолі. - Такі віконниці вішалися на вікна венеціанських будинків, заважаючи вуличним перехожим бачити, що сидять біля вікон дам і черниць».

Помножимо цим способом 347 на 29. Накреслимо таблицю, запишемо над нею число 347, а праворуч число 29.

У кожну стрічку запишемо добуток цифр, що стоять над цією клітиною і праворуч від неї, при цьому цифру десятків добутку напишемо над косою рисою, а цифру одиниць - під нею. Тепер додаємо числа в кожній косій смузі, виконуючи цю операцію, справа наліво. Якщо сума виявиться менше 10, то її пишемо під нижньою цифрою смуги. Якщо ж вона виявиться більше, ніж 10, то пишемо тільки цифру одиниць суми, а цифру десятків додаємо до наступної суми. В результаті отримуємо шуканий добуток 10063.

 

           3                     4                     7

 

 2

 

 

 9

 

10          0                      6                   3

 

 

 

Селянський спосіб множення.

Самим, на мій погляд, «рідним» і легким способом множення є спосіб, який вживали селяни. Цей прийом взагалі не вимагає знання таблиці множення далі числа 2. Сутність його в тому, що множення будь-яких двох чисел зводиться до ряду послідовних поділів одного числа навпіл при одночасному подвоєнні іншого числа. Розподіл навпіл продовжують до тих пір, поки не вийде 1, паралельно подвоюючи інше число. Останнє подвоєне число і дає шуканий результат.

У разі непарного числа треба відкинути одиницю і ділити залишок навпіл; але зате до останнього числа правого стовпця потрібно буде додати всі ті числа цього стовпця, які стоять проти непарних чисел лівого стовпця: сума і буде шуканим добутком:

 

37.......... 32

74.......... 16

148.......... 8

296.......... 4

592.......... 2

1184.......... 1

 

Добуток всіх пар відповідних чисел однаковий, тому

 

37 ∙ 32 = 1184 ∙ 1 = 1184

 

У разі, коли одне з чисел непарне або обидва числа непарні, діємо таким чином :

 

24 ∙ 17

24 ∙ 16 =

= 48 ∙ 8 =

= 96 ∙ 4 =

= 192 ∙ 2 =

= 384 ∙ 1 = 384

24 ∙ 17 = 24 ∙ ( 16 +1 ) = 24 ∙ 16 + 24 = 384 + 24 = 408

 

Новий спосіб множення.

Цікавий новий спосіб множення, про який нещодавно з'явилися повідомлення. Винахідник нової системи усного рахунку кандидат філософських наук Василь Оконешніков стверджує, що людина здатна запам'ятовувати величезний запас інформації, головне - як цю інформацію розташувати. На думку самого вченого, найбільш виграшною в цьому відношенні є девятерічня система - всі дані просто розташовують у дев'яти комірках, розташованих, як кнопочки на калькуляторі.

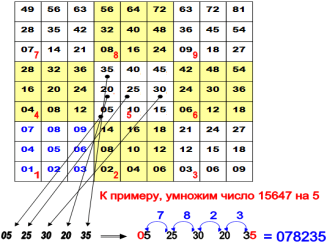
Рахувати по такій таблиці дуже просто. Наприклад, помножимо число 15647 на 5. У частині таблиці, відповідної п'ятірки, вибираємо числа, відповідні цифрам числа по порядку: одиниці, п'ятірці, шістці, четвірці і сімці. Одержуємо: 05 25 30 20 35

Ліву цифру (у нашому прикладі - нуль ) залишаємо без змін, а наступні цифри складаємо попарно: п'ятірку з двійкою, п'ятірку з трійкою, нуль з двійкою, нуль з трійкою. Остання цифра також без змін.

У результаті отримуємо: 078235. Число 78235 і є результат множення.

Якщо ж при складанні двох цифр виходить число, що перевершує дев'ять, то його перша цифра додається до попередньої цифрі результату, а друга пишеться на «своє» місце.

 

 

Множення графічним способом.

Рахункові палички — необхідний атрибут першокласника. На уроках математики початкової школи з їх допомогою відпрацьовують навики додавання і віднімання. А Ви коли-небудь замислювалися, що з їх допомогою можна і перемножувати, досить швидко і легко багатозначні числа? Звичайно, на паличках не зовсім зручно множити числа, а ось на листку паперу, малюючи лінії — запросто. Такий спосіб множення доступний кожному.

Ми вже розглянули, як на пальцях можна множити числа на 6,7,8 і 9. (див. вище). Пальців для багатозначних чисел не вистачить, тому беремо листок паперу і олівець.

 

Отже, множення багатозначних чисел.

 

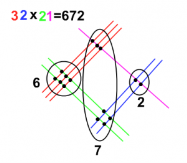Припустимо треба помножити 32 на 21.

На аркуші паперу по черзі малюємо лінії, кількість яких визначається з даного прикладу.

Спочатку 32: 3 червоні лінії і трохи нижче — 2 сині. Потім 21 перпендикулярно вже намальованим, малюємо спочатку 2 зелені, потім — 1 малинову. ВАЖЛИВО: лінії першого числа малюються в напрямку з верхнього лівого кута в нижній правий, другого числа — з нижнього лівого, у верхній правий. Потім рахуємо кількість точок перетину у кожній з трьох областей (на малюнку області позначені у вигляді кіл). Отже, в першій області (область сотень) — 6 точок, у другій (область десятків) — 7 точок, у третій (область одиниць) — 2 точки. Отже відповідь: 672.

Розберемо інший приклад: 123х412 = 50676

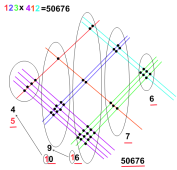Спочатку 123: 1 червону лінію і трохи нижче — 2 сині, і далі — 3 зелені. Потім 412: перпендикулярно вже намальованим, малюємо спочатку 4 фіолетових, потім 1 помаранчеву і 2 блакитних. За аналогією з попереднім прикладом, обводимо області перетинів колами. Всього їх вийшло 5, значить відповідь — п’ятизначне число. Знайдемо його: у першій області 4 точки перетину, у другій — 10, у третій — 16, в четвертій — 7 і в п’ятій — 6. Ті області, де кількість точок вийшло однозначною, складності не викликають, тому почнемо розбирати третю область, де 16 точок перетину: від 16 до цієї області залишаємо тільки останню цифру, а значить 6, все інше (а значить — 1) переносимо в сусідню область справа наліво, отже в третій області залишилося число 6, а в другій тепер до наявних 9 точок треба додати перенесену одиницю. Отже, у другій області тепер 10 точок, а це знову не однозначне число, значить 0 залишимо в другій області, а одиницю перенесемо в першу — тепер у першій на одну точку більше, а значить 5. Складемо відповідь: 50676.

В школі досить часто просять вирішити якусь задачу кількома способами: аналітичним, графічним …, але не множення багатозначних чисел, такий спосіб множення не має право на життя в школі, там множать зазвичай в стовпчик, але це не означає, що він не заслуговує на увагу.