Трикутники. Їх види. Обчислення площі.
Систематизовано основні теоретичні відомості про трикутники, їх види і формули для обчислення їхніх площ. Наведено приклади використання традиційних та маловживаних формул до обчислення площі фігури
1
Обчислення площі трикутників
1.1. Історичні відомості
Основою основ науково-технічного прогресу є подальший розвиток науки, зокрема математики, прикладне значення якої дуже велике. А всебічний розвиток будь-якої науки неможливий без глибокого аналізу її історії. Лейбніц застерігав, що хто хоче обмежитися сучасним без знання минулого, той ніколи не зрозуміє сучасного.
Історія математики має особливу привабливість. Задачі і теореми, доведені сотні і тисячі років тому, захоплюють нас своєю красою, витонченістю логічних міркувань так само, як захоплювали всі попередні покоління.
Перегортаючи сторінки минулого науки, ми переконуємось, що найбільші поклади математичних ідей, понять, задач містяться у практичній діяльності людини.
Зміцнення централізованих держав сприяло створенню міст, розвитку торгівлі. Виникали математичні задачі, зв'язані з виміром площ полів, об'ємів гребель і зерносховищ і т. д. Термінів “трикутник”, “чотирикутник”, “фігура” тоді ще не було. У папірусах, що дійшли до нас, мова йшла про пряме, косе чи кругле поле, ділянку з границею, довжиною і шириною. Площі прямокутників, трикутників і трапецій древні люди вже тоді обчислювали за точними правилами, що зайвий раз доводило, наскільки важливими для повсякденного життя були ці прості геометричні фігури.
У Древній Греції протягом трьох століть учені створили теорії, глибину яких змогли по-справжньому зрозуміти й оцінити лише математики XIX-XX століть. Слава засновника давньогрецької математики належить Піфагору Самоському, що перетворив геометрію зі зборів рецептів рішень різних задач в абстрактну науку. Ця наука розглядає вже не площі полів, місткість зерносховищ, дамб чи штабелів цегли, а геометричні фігури-абстракції, ідеалізації визначених властивостей реальних об'єктів.
З часом знання людства в галузі геометрії розширювалися й удосконалювалися, але не вгасав науковий і практичний інтерес до найпростіших геометричних фігур, зокрема до трикутника – плоскої фігури, утвореної з'єднанням трьох точок прямими лініями. Математики його іменують двовимірним симплексом. «Симплекс» латиною означає найпростіший. Тривимірним симплексом називають трикутну піраміду. Саме через свою простоту трикутник став основою вимірювань.
За допомогою піфагорових трійок можна утворити скільки завгодно трикутників, у яких довжини сторін і площі виражаються натуральними числами. Піфагор довів теорему, в якій площа квадрата, побудованого на гіпотенузі прямокутного трикутника, рівновелика сумі площ квадратів, побудованих на його катетах. У давньогрецьких математиків навіть числа називалися квадратні – n2 і прямокутні – n(n+1). Герон Олександрійський знаходить формулу, що виражає площу трикутника через його сторони; стає відомим, що бісектриси, як медіани та висоти, перетинаються в одній точці.
Особливо активно властивості трикутника досліджувалися в XV-XVI століттях. Ось одна з найкрасивіших теорем того часу, що належить Леонардові Ейлеру: «Середини сторін трикутника, основи його висот і середини відрізків висот від вершини до точки їх перетину лежать на одному колі». Це коло дістало назву «кола дев’яти точок». Його центр виявився в середині відрізка, який з’єднує точку перетину висот з центром описаного кола.
Як відомо, імператор Франції Наполеон вільний час присвячував заняттям математикою. Йому приписують таку красиву теорему: «Якщо на сторонах трикутника в зовнішній бік побудувати рівносторонні трикутники, то їхні центри будуть вершинами рівностороннього трикутника». Цей трикутник називається зовнішнім трикутником Наполеона.
Сила-силенна робіт з геометрії трикутника, проведених у XV-XIX ст., створила враження, що про трикутник уже відомо все. Тим дивовижнішим було відкриття, зроблене американським математиком Ф.Морлі. Він довів, що коли в трикутнику провести через вершини промені, які поділяють кути на три однакові частини, то точки перетину суміжних трисектрис кутів є вершинами рівностороннього трикутника.
1.2. Загальні відомості про трикутники
Систематизуємо основні теоретичні відомості про трикутники, їх види і формули для обчислення їхніх площ.
Трикутником називається фігура, яка складається з трьох точок, що не лежать на одній прямій і трьох відрізків, що послідовно їх сполучають.
Дані точки називаються вершинами трикутника, а відрізки, що їх з’єднують, - сторонами трикутника.
 В
В
А С
Рис. 1.1
Усім відомі рівносторонні, рівнобедрені, тупо- і гострокутні трикутники, прямокутні трикутники, що широко використовуються для рішення простих задач повсякденного життя (побудови інших плоских і просторових фігур, обчислень площ, об’ємів і т.д.). Менш відомі деякі інші види трикутників, наприклад:
- педальний трикутник – трикутник, вершини якого є основами перпендикулярів, опущених з довільної точки Р, що знаходиться у середині трикутника АВС на сторони трикутника АВС;
- ортоцентральний трикутник – окремий випадок педального трикутника, при якому довільна точка Р є точкою перетину висот трикутника АВС;
- серединний трикутник (щодо трикутника АВС) – трикутник, побудований шляхом з'єднання середин сторін даного трикутника АВС;
- різницевий трикутник – трикутник, довжини сторін якого складають арифметичну прогресію;
- бісектральний трикутник – трикутник, вершинами якого є точки перетину бісектрис даного трикутника АВС із протилежними сторонами.
З розвитком науки про трикутники в побут учених (та й не тільки їх) увійшли характерні назви деяких точок і ліній трикутника:
- чевіана – відрізок, що з'єднує вершину трикутника з деякою точкою на протилежній стороні;
- висота – чевіана, опущена під прямим кутом на протилежну сторону трикутника;
- бісектриса – чевіана, що поділяє навпіл кут при даній вершині, з якої вона опущена;
- медіана – чевіана, що з'єднує вершину трикутника із серединою протилежної сторони;
- центр кола, описаного навколо трикутника, точка перетину трьох перпендикулярів, що поділяють навпіл сторони трикутника;
- центр кола, вписаного в трикутник, точка перетину бісектрис трикутника; ортоцентр трикутника АВС – центр кола, вписаного в ортоцентричний трикутник відносно трикутника АВС;
- центроїд – точка, що поділяє відстань від ортоцентра до центра описаного навколо трикутника кола у відношенні 2:1;
- пряма Ейлера – пряма, що з'єднує ортоцентр, центроїд і центр описаного навколо трикутника кола;
- коло дев'яти точок (коло Ейлера) – коло, на якому лежали основи трьох висот довільного трикутника, середини трьох його сторін і середини трьох відрізків, що з'єднують його вершини з ортоцентром.
Трикутник-це многокутник, у якого n=3 (з трьома кутами і трьома сторонами). Сторони і кути трикутника вважаються основними елементами трикутника. У трикутнику проти більшого кута лежить більша сторона, а проти меншого-менша.
Трикутник повністю визначається будь-якою з таких трійок своїх основних елементів: або трьома сторонами, або однією стороною і двома кутами, або двома сторонами і кутом між ними. Тобто це є ознаки рівності трикутників.
Також для існування трикутника, заданого трьома сторонами a, b, c необхідно і достатньо, щоб виконувалися нерівності, які називаються нерівностями трикутника: a + b > c, a + c > b, d +c > a, де a, b, c його сторони.
Математика – складна наука, що вимагає запам’ятовування і вміння оперувати великою кількістю формул. Розглянемо конкретну ситуацію, перед Вами завдання: знайдіть площу трикутника abc. З чого почати?
Площа — величина, що визначає розмір поверхні, одна з основних властивостей геометричних фігур. Площу нескладних геометричних фігур можна визначити двома способами: 1) підраховувати кількість одиничних квадратів, якими фігури можна покрити; 2) за допомогою відповідної формули.
До будь-якій задачі такого типу застосовна схема дій: виділити, що дано (тип трикутника, дані елементи і т.п.) – вибрати відповідну формулу, яка дозволить за вихідними даними знайти відповідь. Тому виділимо найбільш поширені формули для відповіді на питання, як знайти площу трикутника.
У шкільні програмі з геометрії восьмого класу, для довільного опуклого трикутника: SΔАВС = ![]() а·hа де а – сторона трикутника, hа – висота проведена до даної сторони. Хоча ця формула й проста, вона може бути використана тільки, якщо можна легко знайти висоту. Наприклад землемір ділянки трикутної форми міряє довжину кожної сторони і може знайти площу без визначення довжини висоти.
а·hа де а – сторона трикутника, hа – висота проведена до даної сторони. Хоча ця формула й проста, вона може бути використана тільки, якщо можна легко знайти висоту. Наприклад землемір ділянки трикутної форми міряє довжину кожної сторони і може знайти площу без визначення довжини висоти.
Учні дев’ятого класу знайомляться з теоремою: «Площа трикутника дорівнює половині добутку двох будь-яких сторін на синус кута між ними». Тобто S = ![]() а ∙b ∙ sinγ.
а ∙b ∙ sinγ.
Форма трикутника однозначно визначається трьома сторонами. Відповідно для того щоб порахувати площу достатньо знати довжину сторін. З цим завдання на відмінно справився Герон. Формула Герона красива, симетрична, зручна, легко запам’ятовується, справжня формула – красуня! Цікава й історія її творення. Називають її ім'ям Герона Олександрійського (Старшого) не зовсім заслужено, бо вперше відкрив і обґрунтував її Архімед. А Герон тільки через чверть тисячоліття після того вмістив її у своїй праці «Метрика». Тому справедливіше було б називати її формулою Архімеда або принаймні Архімеда – Герона. Отже, ![]() , де
, де ![]() .
.
У підручниках з геометрії можна знайти формули для знаходження площ окремих видів трикутників.
Рівносторонній трикутник — це трикутник, усі сторони якого рівні. В Евклідовій геометрії всі три кути рівностороннього трикутника також рівні. Тому рівносторонні трикутники є правильними багатокутниками і мають назву правильних. Нехай довжина ребра правильного трикутника дорівнює ![]() , тоді: площа дорівнює S =
, тоді: площа дорівнює S = ![]() .
.
Площа прямокутного трикутника (один із кутів якого дорівнює 900) з катетами a і b рівна половині їх добутку S = ![]() а ∙ b.
а ∙ b.
Поширеним явищем в геометрії є многокутники описані та вписані в коло. Трикутник не виключення. Для довільного трикутника, формула для знаходження площі, у якого задано три сторони a, b, c та радіус R кола, описаного навколо нього має вигляд: ![]() . Для правильного вписаного в коло трикутника
. Для правильного вписаного в коло трикутника 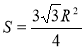 .
.
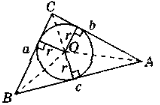 Площу трикутника, в який вписано коло можна визначити S=r·p, де p-півпериметр (рис.1.2). Для рівностороннього трикутника
Площу трикутника, в який вписано коло можна визначити S=r·p, де p-півпериметр (рис.1.2). Для рівностороннього трикутника ![]() r2. Рис.1.2
r2. Рис.1.2
Всі вище названі формули вивчаються в курсі геометрії 8 і 9 класу. Але є ще й такі, які у підручниках не зустрічаються.
- Маловживані формули для розрахунку площі трикутників
Тригонометричний спосіб.
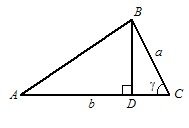 Одна з найпоширеніших формул, що дає можливість знайти площу трикутника за відомими стронами та кутом між ними має вигляд:
Одна з найпоширеніших формул, що дає можливість знайти площу трикутника за відомими стронами та кутом між ними має вигляд:
![]()
Рис. 1.3.
Крім того, sin α = sin (π - α) = sin (β + γ), що справедливо і для інших двох кутів. Тому площу трикутника можна визначити так:
![]()
Знаючи сторону і два кути, один з яких прилеглий:
![]()
і аналогічно якщо відомі сторони a чи c.
Якщо необхідно визначити площу трикутника за відомою стороною і двома прилеглими кутами, можна скористатися формулами:
![]()
Формула Герона та способи її запису.
Форма трикутника однозначно визначається трьома сторонами. Відповідно для того щоб порахувати площу достатньо знати довжини його сторін. За формулою Герона:
![]()
де ![]() — півпериметр
— півпериметр
Здійснивши тотожні перетворення, можна отримати інші способи запису формули Герона:
![]()
![]()
![]()
Останню формулу досить часто використовують в коді програм калькуляторів
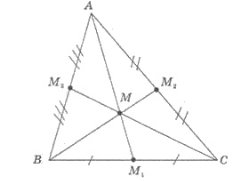 Формули, схожі на формулу Герона.
Формули, схожі на формулу Герона.
Є три формули, що мають схожий вигляд як формула Герона, але записані через інші величини. Спочатку позначимо, що медіани для сторін a, b, і c відповідно як ![]() і
і ![]() , а їхню півсуму
, а їхню півсуму ![]() як
як ![]() , маємо
, маємо
![]()
![]()
Позначимо висоти на сторони a, b, і c відповідно як ![]() ,
, ![]() , і
, і ![]() ,і позначимо на півсуму величин обернених до висот як тоді маємо:
,і позначимо на півсуму величин обернених до висот як тоді маємо:
![]()
![]()
Якщо позначити на півсуму синусів кутів як
![]() ,
,
тоді матимемо:
![]()
де D — діаметр описаного кола:
![]()
Існують також інші формули для обчислення площі, наприклад
![]()
Для діаметра описаного кола D.
РОЗДІЛ 2
Застосування нових формул до розв’язування задач

 Задача 1. Діагональ паралелограма ділить гострий кут на кути 30о і 45о. Сторона, що лежить проти кута 45о, дорівнює 10см. Знайдіть площу паралелограма.
Задача 1. Діагональ паралелограма ділить гострий кут на кути 30о і 45о. Сторона, що лежить проти кута 45о, дорівнює 10см. Знайдіть площу паралелограма.
В С Нехай АВСD – паралелограм, АС – діагональ
паралелограма. ![]() ВАС =45о,
ВАС =45о, ![]() САD=30о, ВС=10см.
САD=30о, ВС=10см.
Знайдемо площу паралелограма.
А D Розв’язання:
І спосіб.
Діагональ паралелограма ділить його на два трикутники рівних за площею. Площу трикутника можна визначити за формулою: S = ![]() аb sinγ, тоді
аb sinγ, тоді
площа паралелограма: S = аb sinγ, де а і b - сторони паралелограма, γ – кут між ними.
![]() ВАD = 30о+45о=75о.
ВАD = 30о+45о=75о.
За властивостями паралелограма: ВС=АD, АВ=СD, ![]() ВАС =
ВАС = ![]() АСD = 45о,
АСD = 45о, ![]() САD =
САD = ![]() АСВ = 30о.
АСВ = 30о.
Розглянемо трикутник АВС. Використавши теорему синусів ![]() , отримаємо: АВ=
, отримаємо: АВ=![]() , АВ=
, АВ=![]() = 5
= 5![]() =7,1 (см).
=7,1 (см).
Тоді площа паралелограма S= аb sinγ =7,1·10·![]()
Відповідь: Площа паралелограма 69(см2).
ІІ спосіб.
Для розв’язування задачі, скористаємось властивістю: площа паралелограма рівна сумі площ трикутників на які він поділяється діагоналлю. Тобто SавсD =2SАВС. Площу трикутника АВС знайдемо за тригонометричною формулою для площі, за відомою стороною і двома кутами, один з яких прилеглий SАВС. =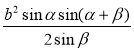 , тому SавсD =
, тому SавсD =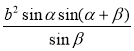 .
.
SавсD =![]() =69 (см2)
=69 (см2)
Відповідь: Площа паралелограма 69(см2).
Як бачимо, другий спосіб має переваги над першим. Завдяки новим формулам можна розв’язувати задачі в два рядки.


про публікацію авторської розробки
Додати розробку
