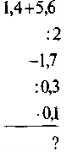Обернено пропорційні величини
Тема. Обернено пропорційні величини
Мета: сформувати уявлення учнів про зміст поняття обернено пропорційних величин; навчити відрізняти прямо і обернено пропорційні величини, розв'язувати обернено пропорційні величини складанням пропорції.
Тип уроку: засвоєння знань, умінь, навичок.
Хід уроку
I. Перевірка домашнього завдання
- Вибіркова перевірка зошитів
- Усні вправи
- Обчисліть:
|
|
|
|
|
-
Чи можна з чисел 3
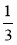 ; 3; 2,5; 4 скласти істинну пропорцію? Якщо так,
; 3; 2,5; 4 скласти істинну пропорцію? Якщо так,
складіть її. -
Маємо дві величини: х і у, їх значення х1 і х2; у1 і у2 такі, що
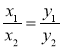 . Що можна сказати про величини х і у?
. Що можна сказати про величини х і у?
- Поділіть число 28 на 3 доданки, пропорційні числам 1; 2; 4.
II. Актуалізація опорних знань
Чи є прямо пропорційними величинами?
а) s і t, якщо v стала;
б) вартість товару, купленого по одній і тій самій ціні, і його кількість;
в) площа квадрата і довжина його сторони;
г) кількість робітників, які виконують якусь роботу з однаковою
продуктивністю праці, і час виконання роботи;
д) ціна товару і його кількість, якщо сталою залишається вартість покупки.
(Дуже важливо під час розбору цього завдання спиратися на життєвий досвід учнів, у випадках виникнення утруднень з пошуком відповіді, пропонувати наводити відповідні числові приклади, в яких спостерігаємо, як зміниться одна з величин за умови збільшення або зменшення другої у кілька разів.)
III. Засвоєння знань
По закінченні виконання усних вправ учні можуть самі дати відповідь на запитання: чи всі величини, що оточують нас, є прямо пропорційними (тобто збільшення (зменшення) якоїсь з величин тягне за собою збільшення (зменшення) іншої величини у стільки ж разів).
Звертаємо увагу на приклади г) і д) і робимо висновок: у цих прикладах дві величини такі, що збільшення однієї в декілька разів тягне за собою зменшення іншої величини у ту саму кількість разів і навпаки — такі величини будемо називати обернено пропорційними. (Можна запропонувати учням спробувати навести інші приклади обернено пропорційних величин з повсякденного життя.)
Окрім розуміння змісту поняття обернено пропорційні величини, маємо навчитися розв'язувати задачу складанням пропорції.
Задача. Для будівництва стадіону 5 бульдозерів розчистили ділянку за 210хв. За який час 7 бульдозерів розчистять цю ділянку?
Розв'язання
Одразу повідомляємо учням, що запис короткої умови задачі робимо так само, як і в задачах на прямо пропорційні величини.
|
|
Кількість бульдозерів |
Час |
||
|
І раз |
|
5 |
210хв |
|
|
ІІ раз |
7 |
х хв |
||
Дуже важливо, щоб учні побачили, що в цій задачі саме обернено пропорційні величини (підключаємо життєвий досвід), і оскільки величини є обернено пропорційними, стрілки ставимо в протилежних напрямках, тому і відношення будемо брати в протилежних напрямках:
![]() =
=![]() ; 7х = 5 · 210;
; 7х = 5 · 210; 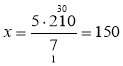 (хв.).
(хв.).
Відповідь. 150 хв.
IV. Формування вмінь
Усні вправи
-
З величин s, v i t виберіть ті, що є (будуть) обернено пропорційними. За
яких умов це буде виконуватися? -
А і В обернено пропорційні величини; а1 і а2; b1 і b2 — їх відповідні значення. Чи правда, що: а)
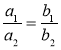 ; б)
; б) 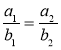 ; в)
; в) 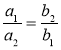 ; г)
; г) 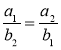 ?
?
Письмові вправи
-
Два прямокутники мають однакову площу. Довжина одного прямо
кутника 8 м, а ширина 4,5 м. Знайдіть довжину другого прямокутника,
якщо його ширина дорівнює 2 м. -
У книжці 448 сторінок, на кожній сторінці 41 рядок, у кожному рядку
в середньому 54 букви. На скількох сторінках може бути передрукована ця книжка, якщо на сторінці буде 48 рядків і в кожному рядку 42 букви. — Обернено пропорційні величини.
Додаткові вправи
-
а) Для перевезення вантажу знадобилось 24 автомобілі вантажністю
7,5 т. Скільки знадобиться автомобілів вантажністю 4,5 т, щоб пере
везти той самий вантаж?
б) Троє мулярів можуть закінчити роботу за 5 днів. Для прискорення
роботи їм дали ще 2-х мулярів. За який час вони закінчать роботу,
якщо всі муляри працюють з однаковою продуктивністю?
в) Розв'яжіть рівняння: а) ![]() ; б)
; б) ![]() .
.
IV. Підсумки уроку
Ігровий момент
Уявіть собі, що на Землі відбулась плутанина і для процесів, що описуються прямою пропорційністю, використовують обернену пропорційність і навпаки.
Тоді б ми говорили:
- Чим більше купуємо цукерок, тим .... (менше сплачуємо грошей).
- Чим довше горить свічка, тим... (вона довша і т. ін.)
Придумайте свої подібні переплутані висновки.
V. Домашнє завдання
-
Є два сувої тканини однакової вартості. У першому сувої 40 м тканини
ціною 28,4 грн за 1 м. Скільки коштує 1 м тканини у другому сувої,
якщо в ньому 32 м тканини? -
Для того щоб побудувати стіну завдовжки 18 м, завтовшки 0,5 м і зав
вишки 3 м, потрібно 10 880 цеглин. Якої висоти стіну можна побуду
вати при довжині 15 м, товщині 0,25 с, маючи 5 400 таких цеглин? - Розв'яжіть рівняння:
а) 3,6х – 4,5 = 15,3; б) 0,4(х + 1,6) = 3,24; в) ![]() .
.


про публікацію авторської розробки
Додати розробку