ТАЄМНИЦЯ ЦИКЛОЇДИ – ГЕОМЕТРИЧНЕ МОДЕЛЮВАННЯ НАВКОЛИШНЬОГО СВІТУ
Міністерство освіти і науки України
Департамент освіти і науки
Львівської облдержадміністрації
ЛЬВІВСЬКЕ ТЕРИТОРІАЛЬНЕ ВІДДІЛЕННЯ МАН України
Відділення: математика
Секція: математичне моделювання
ТАЄМНИЦЯ ЦИКЛОЇДИ – ГЕОМЕТРИЧНЕ МОДЕЛЮВАННЯ НАВКОЛИШНЬОГО СВІТУ
Роботу виконав:
Кулявець Тарас Андрійович
Учень 11 класу
Сокальського НВК «ЗШ I ст.-
гімназія» ім.О.Романіва
Слухач Малої академії наук
м.Сокаль
Науковий керівник:
Кровіцька Лариса Ярославівна
Вчитель математики Сокальської
Малої академії наук
учнівської молоді
Сокаль-2018
ЗМІСТ
РОЗДІЛ I. ВІДОМОСТІ ПРО ЦИКЛОЇДУ ТА ЇЇ ВЛАСТИВОСТІ
1.1. Історія походження циклоїди.
1.2. Побудова циклоїди по точках. Механічне та параметричне означення циклоїди. Рівняння циклоїди.
РОЗДІЛ II. ЗАСТОСУВАННЯ ЦИКЛОЇДИ
2.1. Застосування зубчастих зачеплень у техніці.
РОЗДІЛ III. ВЛАСНІ ДОСЛІДЖЕННЯ
3.1. Узагальнення відомих формул.
3.2. Поділ арки циклоїди у заданому відношенні.
3.3. Цікаві відношення довжин дуг циклоїди. Відрізки і кути під аркою циклоїди.
Немає більш природного прагнення,
ніж прагнення до пізнання.
Мішель Монтень
Сучасна людина живе в світ, що рухається постійно вперед. Вона повинна вміти користуватися і володіти всіма засобами існування: знаннями, здобутими вміннями, комп’ютером, транспортними засобами, володіння якими в наш час стає не розкішшю, а потребую. Для цього, щоб бути фахівцем в цій справі ми повинні цікавитися будовою окремих елементів транспортного засобу. Кажуть, що коли людина знає математику, то вона знає все. Безперечно, без математики не відбувається жоден рух, жодне пересування.
Математичний аналіз – частина математики, в якій функції та їх узагальнення вивчають методами диференціального та інтегрального числення. З виникненням математичного аналізу математиці стало доступне вивчення і відображення процесів реального світу; до математики увійшли змінні величини і рух.
Циклоїда – траєкторія руху точки на ободі колеса під час прямолінійного руху транспортного засобу. Робота актуальна, адже властивості циклоїди знаходять застосування в технічних розрахунках механізмів, деталі яких виконують обертальні та поступальні рухи.
Предмет дослідження: задача про довжину арки та циклоїду, співвідношення довжин дуг арки циклоїди.
Мета дослідження: вивчити, дослідити і узагальнити задачі про поділ арки циклоїди, і обчислити довжини дуг арки циклоїди.
Власні дослідження були спрямовані на розв'язання окремих задач у загальному вигляді, пошук нових закономірностей та відношень між елементами циклоїди.
У висновках вказано, які поставлені проблеми вирішено, а які є перспективними для подальших досліджень.
Додатки містять відомості про біографії математиків 17 століття, у наукових працях яких циклоїда посіяла чільне місце, які сформулювали властивості та знайшли їм практичне застосування. Також у додатках надаються розв'язки задач і теоретичні відомості з теми дослідження.
Першим, хто став вивчати циклоїди був Галілео Галілей - знаменитий італійський астроном, фізик, учений. Саме він придумав назву цієї кривої. «Циклоїда» - та, що породжена кругом. Той факт, що циклоїда згадується навіть у художній літературі, також свідчить про те, що цікавою вона була не лише математикам. Жоден із визначних математиків не обійшов циклоїду своєю увагою.
Про це свідчать і синоніми до слова циклоїда:
- рулетта - французький термін від слова rouler – котити;
- трохоїда - грецький еквівалент назв рулетта і циклоїда;
- таутохрона - від грецьк. tauto - те ж саме + хроvos – час;
- брахістохрона - від грецьк. врахіоtos - найкоротший і грецьк. хроvos – час.
Навіть походження цих слів говорить про палку дискусію, кому належав пріоритет у відкритті циклоїди.
Отже, об’єкт дослідження: циклоїда та задачі про неї.
Завдання дослідження:
- отримати формули на поставлені запитання;
- узагальнити й систематизувати отримані результати.
РОЗДІЛ I. ВІДОМОСТІ ПРО ЦИКЛОЇДУ ТА ЇЇ ВЛАСТИВОСТІ
1.1. Історія походження циклоїди.
Авторитетним джерелом інформації про циклоїду є «Історія рулетти або трохоїди» (1658 р.), автором якої був французький математик, механік, фізик, філософ - Блез Паскаль. Він висловлює свій подив з приводу того, що математики древності не розгледіли її: «Рулетта є лінією настільки звичайною, що після прямої та кола немає лінії, що трапляється частіше. Отже, дякуючи Паскалю, маємо механічне визначення: циклоїда - плоска крива, яку описує фіксована точка, нерухомо зв'язана з колом, що котиться по нерухомій прямій.
Якщо точка М розташована на колі, то під час обертання кола по прямій отримаємо звичайну циклоїду ( рис. 1).
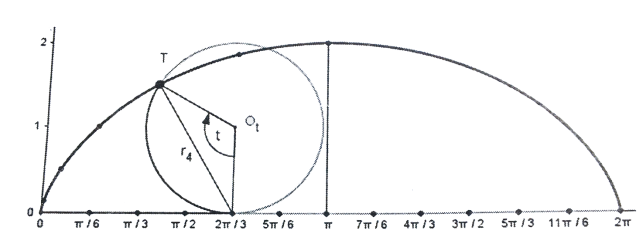
Рис. 1. Звичайна циклоїда

Рис. 2. Видовжена циклоїда
Якщо точка К розташована всередині кола, отримаємо вкорочену циклоїду
( рис. 3).

Рис. 3. Вкорочена циклоїда
Саме такі траєкторії мають точки, розташовані на колесі вагона поїзда, що рухається по колії (осі х).
1.2. Побудова циклоїди по точках. Механічне та параметричне означення циклоїди. Рівняння циклоїди.
Опишемо побудову циклоїди по точках, якщо r = 2см, то ![]() Відкладемо на прямій відрізок, рівний довжині кола. Коло й відрізок поділимо на 12 рівних частин. Виконаємо побудови, як показано на рис.4.
Відкладемо на прямій відрізок, рівний довжині кола. Коло й відрізок поділимо на 12 рівних частин. Виконаємо побудови, як показано на рис.4.

Рис. 4. Побудова циклоїди
Для побудови точного графіка можна використати можливості графічних редакторів.
Назвемо на прикладі першої арки елементи циклоїди. Відрізок А0А12 – основа циклоїди, точка ![]() – вершина циклоїди, пряма А6О6 – вертикальна вісь симетрії циклоїди, точки А0, А12 – точки повернення, твірний круг радіуса r, який утворює нескінченний ряд арок.
– вершина циклоїди, пряма А6О6 – вертикальна вісь симетрії циклоїди, точки А0, А12 – точки повернення, твірний круг радіуса r, який утворює нескінченний ряд арок.
Ми вже навели кінетичне означення циклоїди. Саме це означення використано для побудови циклоїди по точках. Можна задати циклоїду параметричним рівнянням:
![]()
( рис.1 )
Рівняння циклоїди в декартових координатах має вигляд:
![]()
Маючи рівняння кривої, можна побудувати її графік, використовуючи можливості ІКТ.
1.3 Дотична та нормаль до циклоїди. Довжина арки. Площа циклоїди.
Циклоїда - це графік періодичної функції з періодом ![]() , де r - радіус твірного круга. Щоб побудувати дотичну до циклоїди у будь-якій її точці, достатньо з'єднати цю точку з найвищою точкою твірного круга. З’єднавши цю точку з найнижчою точкою твірного круга, отримаємо в цій точці нормаль (кут, що спирається на діаметр кола, прямий!). Радіус кривизни кожної точки циклоїди визначається за формулою 4r
, де r - радіус твірного круга. Щоб побудувати дотичну до циклоїди у будь-якій її точці, достатньо з'єднати цю точку з найвищою точкою твірного круга. З’єднавши цю точку з найнижчою точкою твірного круга, отримаємо в цій точці нормаль (кут, що спирається на діаметр кола, прямий!). Радіус кривизни кожної точки циклоїди визначається за формулою 4r ![]() (рис.5).
(рис.5).
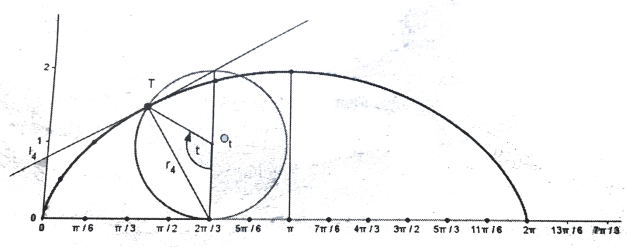
Рис.5. Дотична і нормаль
Довжина арки циклоїди дорівнює 8r або 4d – чотири діаметри твірного круга. Першим це обчислив експериментально Крістофер Рен у 1658 році. Пізніше Гюйгенс, працюючи над циклоїдальним маятником, отримав такий самий результат, що підтвердив попередній.
Площа, обмежена аркою циклоїди та її основи, дорівнює ![]() що експериментально встановив Галілей, тобто ця площа дорівнює потроєній площі твірного круга.
що експериментально встановив Галілей, тобто ця площа дорівнює потроєній площі твірного круга.
Циклоїда є брахістохроною, тобто кривою найшвидшого спуску. Експериментально це встановив Галілей. У 1696 році відповідну задачу сформулював і дослідив Якоб Бернуллі.
Задача Бернуллі. Через точки B та A, що лежать на різній висоті над землею, провести криву, рухаючись по якій лише під дією сили тяжіння, тіло пройде шлях з B до A за найкоротший час.
Бернуллі, досліджуючи властивість брахістохронності, встановив, що такою красивою є перевернута циклоїда, причому фініш розташований у вершині циклоїди. До слова, задача найшвидшого спуску цікавила математиків і раніше. Галілео Галілей, наприклад, вважав траєкторією найшвидшого спуску четвертинку кола. Це було помилкою (рис. 6).


Рис.6. Брахістохрона
Циклоїдa є таутохроною. Дослідження цієї властивості належить Гюйтенсу. Як і Галілей, він працював над створенням механізмів (годинників) точного вимірювання часу. Задумавшись над тим, якою має бути траєкторія руху маятника або грузу, щоб період коливань не залежав від амплітуди (початкового положення), Гюйгенс дійшов висновку: це перевернута циклоїда! (рис. 7) .

Рис. 7. Період коливання маятника не залежить від амплітуди.
Треба віддати належне винахідливості Гюйгенса.
Щоб змусити вантаж рухатися по циклоїді, він знайшов просте й геніальне рішення: рух нитки маятника він направляє за допомогою таких собі «щік» у вигляді четвертинок перевернутої циклоїди (рис. 8).

Рис. 8. Рух нитки маятника за допомогою четвертинок перевернутої циклоїди
Намотуючись на «щоки», груз на кінці нитки рухається по такій самій циклоїді, лише опущеній униз та зсунутій убік на половину арки. Так Гюйгенс показав, що еволютою циклоїди є така сама здвигнута циклоїда.
РОЗДІЛ II. ЗАСТОСУВАННЯ ЦИКЛОЇДИ
2.1. Застосування зубчастих зачеплень у техніці.
Оскільки деталі машин, механізмів, що здійснюють одночасно поступальний та обертальний рухи, описують циклоїди, то властивості циклоїди знаходять практичне застосування в техніці. Зокрема, профілі зубів шестерень, обрис багатьох типів ексцентриків, кулачків та інших деталей машин мають форму саме циклоїди (рис. 9).
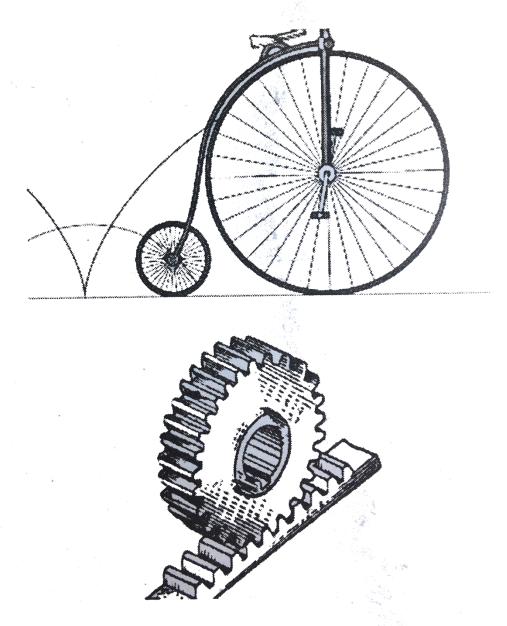
Рис. 9. Застосування зубчастих зачеплень у техніці
Ще раз нагадаємо, що циклоїда була грунтовно досліджена Б. Паскалем та його сучасниками й послідовниками. Вони вирішили пов'язані з нею задачі. Описуючи властивості циклоїди, ми навели результати цих досліджень, такі як: а) побудова дотичної та нормалі у будь-якій точці циклоїди;
б) довжина арки 8r;
в) площа під аркою ![]() .
.
На жаль, у літературі ми не змогли знайти оригінали, а лише розв'язки цих задач методами диференціального і інтегрального числення. Наведемо приклади лише тих задач, що були узагальнені й використані нами для подальших досліджень. А саме: розглянемо задачі про обчислення довжини арки циклоїди та площу, обмежену аркою та основою циклоїди.
- Для кривої, що задана пара метрично, довжина дуги обчислюється за формулою
l=![]() dt
dt
- Для першої арки циклоїди:
![]()
![]()
![]()
l=![]() dt=
dt=
=![]() dt=
dt=
= ![]() =
= ![]() =
=
= r ![]() =
=
= r ![]()
![]() = r
= r ![]() dt = 2r
dt = 2r![]()
![]() =
=
= 4r ![]()
![]()
![]() = 4r
= 4r![]() (1+1) = 8r
(1+1) = 8r
- Для параметрично заданої кривої обмежена нею площа обчислюється за формулою:
S = ![]()
Для першої арки циклоїди
S = ![]() =
=
= ![]() dt =
dt = ![]() =
=
= ![]()
![]()
![]()
![]() 1 – 2
1 – 2 ![]() +
+![]() ) dt =
) dt =
= ![]()
![]() ) dt =
) dt =
= ![]()
![]()
![]() dt =
dt = ![]()
![]()
![]() =
=
= ![]()
![]() =
=
= ![]() ( 6π – 0 + 0 ) = 3 π
( 6π – 0 + 0 ) = 3 π![]() - потроєна площа твірного круга.
- потроєна площа твірного круга.
РОЗДІЛ III. ВЛАСНІ ДОСЛІДЖЕННЯ
3.1. Узагальнення відомих формул.
Враховуючи відомі формули тригонометрії, а саме:
![]() , або
, або ![]() , звідки
, звідки ![]() , або
, або ![]() ,
,
![]() або
або![]() , запишемо рівняння циклоїди інакше:
, запишемо рівняння циклоїди інакше:
![]()
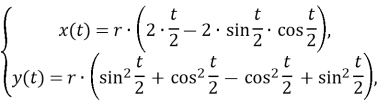
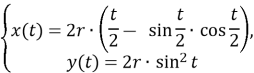
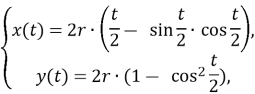
Тепер розглянемо довжину дуги арки та площу під нею як функції від ![]() :
:
![]() – довжина дуги AB,
– довжина дуги AB,
![]() – площа під нею.
– площа під нею.
Точка B має координати ![]() і
і ![]() , тобто B
, тобто B ![]() (рис. 10).
(рис. 10).
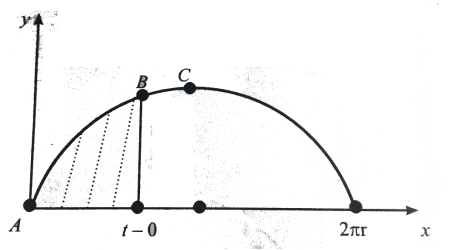
Рис. 10
Зауважимо, що l(0) = 0, l(2πr) = 8r, S(0)=0, S(2π) = 3π![]()
Запишемо формули для l(t) та S(t).
l(t)= ![]() dt
dt
S(t)=![]() dt
dt
l(t)=![]() dt= r
dt= r![]() =
=
=r![]() dt = r
dt = r![]() dt=
dt=
= 4r![]()
![]() (1)
(1)
S(t)=![]() dt= r
dt= r![]() =
=
=![]() dt=
dt=
=![]() dt=
dt=
= ![]() =
= ![]() =
=
= ![]()
![]() =
=
= ![]() =
=
= ![]()
Отже, S(t) = ![]() (2)
(2)
3.2. Поділ арки циклоїди у заданому відношенні.
Тепер сформулюймо задачу про поділ дуги циклоїди у довільному відношенні. Враховуючи симетрію, можна розглядати половину арки циклоїди (рис. 11), а саме:
![]()
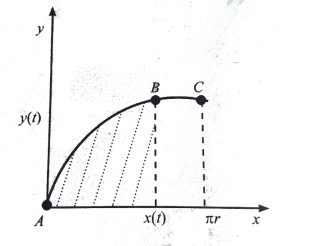
Рис. 11
Задача. Дуга ABC – половина арки циклоїди. Знайти:
1) значення параметра t, при якому точка В ділить дуги ABC у відношенні m:n.
2) довжини дуг АВ і ВС.
3) координати точки В (x(t); y(t)).
4) Прощу під дугою AB.
Розв`язання. Оскільки довжина всієї арки 8r, то довжина дуги AC = 4r. Нехай точка В ділить ABC у відношенні m:n. Позначимо відповідне значення
t = t m, n, довжину дуги AB = l m, n = l (t m, n).
X m, n = x (t, m, n), Y m, n = y (t, m, n) – координати точки B, S m, n = S (t, m, n) – площа, обмежена дугою AB.
![]() , тоді
, тоді
![]()
![]()
![]() за формулою (1).
за формулою (1).
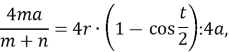
![]()
![]()
![]()
![]()
![]()
![]() .
.
Знайдемо координати точки B, що відповідають цьому значенню параметра t. Для цього підставимо його у рівняння циклоїди. Отримаємо:
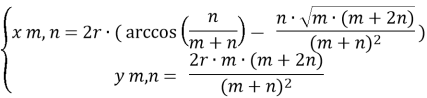
І нарешті, обчислимо площу під дугою AB. Використаємо отриману нами формулу (2).
S m, n = ![]()
S m, n = ![]()
S m, n = ![]()
Візьмемо кілька конкретних значень m і n.
![]()
![]()
Отримали відомий результат: горизонтальна пряма ![]() ділить арку циклоїди на три рівні частини (рис. 12), а саме:
ділить арку циклоїди на три рівні частини (рис. 12), а саме:
![]()
![]()
![]()
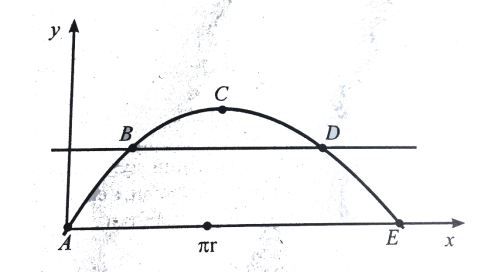
Рис. 12
Тоді пряма ![]() поділить арку у відношенні 1:2:1
поділить арку у відношенні 1:2:1 ![]() .
.
3.3. Цікаві відношення довжин дуг циклоїди. Відрізки і кути під аркою циклоїди.
Ще одна цікава властивість довжин дуг арки циклoїди помічена нами в результаті наступних досліджень. Використаємо формулу (1) та обчислимо довжини дуг першої арки циклоїди, що відповідають значенням таблиці 1 параметра t, а саме 0;![]() ;
;![]()
- t =
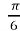 ;
; 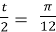 , cos
, cos  =
= 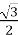 ,
, 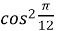 =
= 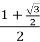 =
= 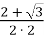 =
= 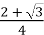 ,
,
cos ![]() ,
,
l![]() = 4r
= 4r![]() , l
, l![]() =2r
=2r ![]()
- t =
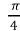 , ;
, ; 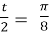 , cos
, cos  =
= 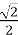 ,
, 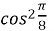 =
= 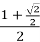 =
= 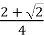 ,
,
cos ![]() ,
,
l![]() = 4r
= 4r![]() , l
, l![]() =2r
=2r ![]() .
.
- t =
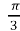 ;
; 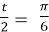 , cos
, cos  =
= 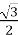 , l
, l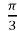 =4r
=4r 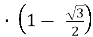 , l
, l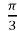 =2r
=2r  .
. - t =
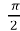 ;
; 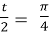 , cos
, cos  =
= 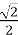 , l
, l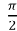 =4r
=4r 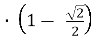 , l
, l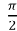 =2r
=2r  5
5
- t =
 ;
; 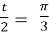 , cos
, cos  =
= 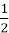 , l
, l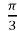 =4r
=4r 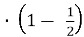 , l
, l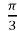 =2r.
=2r.
- t =
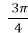 , ;
, ; 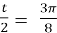 , cos
, cos 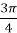 =
= 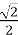 ,
, 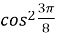 =
= 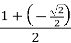 =
= 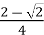 ,
,
cos ![]() ,
,
l![]() = 4r
= 4r![]() , l
, l![]() = 2r
= 2r ![]() .
.
- t =
 ;
; 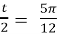 , cos
, cos 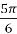 =
= 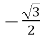 ,
, 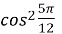 =
= 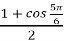 =
= 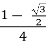 ,
,
cos ![]() ,
,
l![]() = 4r
= 4r![]() , l
, l![]() = 2r
= 2r ![]()
- t = π,
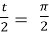 , cos
, cos  =
= 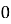 , lπ = 4r.
, lπ = 4r.
Обчислюючи подальші довжини дуг, враховуємо, що π ![]()
![]()
![]()
![]()
l![]() =8r - l
=8r - l![]() і т.д.
і т.д.
- t =
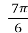 ;
; 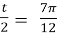 , cos
, cos 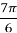 =
= 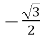 ,
, 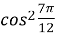 =
= 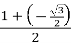 =
=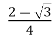 ,
,
cos ![]() ,
,
l![]() = 4r
= 4r![]() , l
, l![]() = 2r
= 2r ![]()
- t =
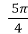 , ;
, ; 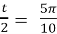 , cos
, cos 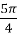 =-
=- 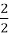 ,
, 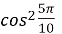 =
= 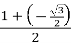 ,
,
![]() , cos
, cos ![]() ,
,
l![]() = 2r
= 2r ![]() .
.
- t =
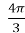 ;
;  , cos
, cos 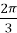 = -
= - 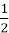 , l
, l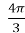 = 4r
= 4r 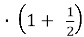 , l
, l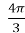 =6r.
=6r.
- t =
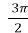 ;
; 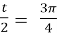 , cos
, cos 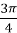 =-
=- 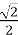 , l
, l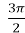 =4r
=4r 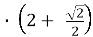 ,
,
l![]() = 2r
= 2r ![]()
- t =
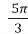 ;
; 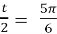 , cos
, cos 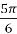 =-
=- 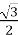 , l
, l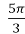 = 2r
= 2r 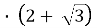 .
. - t =
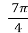 , ;
, ; 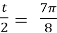 , cos
, cos 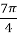 =
= 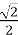 ,
, 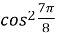 =
= 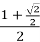 ,
,
cos ![]() ,
,
l![]() = 2r
= 2r![]() .
.
- t =
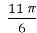 ;
; 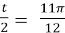 , cos
, cos 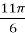 =
= 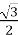 ,
, 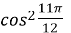 =
= 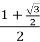 =
= 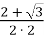 =
= 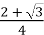 ,
,
cos ![]() , l
, l![]() = 2r
= 2r![]() .
.
-
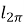 =8r.
=8r.
Запишемо отримані результати в таблицю 1. Таблиця 1
|
№ |
t |
|
|
1 |
|
2r |
|
2 |
|
2r |
|
3 |
|
2r |
|
4 |
|
2r |
|
5 |
|
2r |
|
6 |
|
2r |
|
7 |
|
2r |
|
8 |
|
4r |
|
9 |
|
2r |
|
10 |
|
2r |
|
11 |
|
6r |
|
12 |
|
2r |
|
13 |
|
2r |
|
14 |
|
2r |
|
15 |
|
2r |
|
16 |
2 |
8r |
З таблиці видно, що довжини дуг, кінці яких симетричні осі арки циклоїди, є спряженим виразами. Знайдемо відповідні добутки. Результати в таблиці 2.
Таблиця 2
|
№ |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
Аналогічні спостереження дали результати таблиці 3.
Таблиця 3
|
№ |
Добуток довжин дуг, що мають спряжені координати |
|
1 |
|
|
2 |
|
|
3 |
|
Нехай r = 1, на відрізку [0; ![]() відмітимо точки, що відповідають числам таблиці 1, тоді добуток всіх чисел з таблиці 1 дорівнює: 8
відмітимо точки, що відповідають числам таблиці 1, тоді добуток всіх чисел з таблиці 1 дорівнює: 8 ![]() 4
4 ![]() 16
16 ![]() 16
16 ![]() 16
16 ![]() 1
1 ![]() 2
2 ![]() 3 = 786432 = 3
3 = 786432 = 3 ![]()
![]() .
.
Зробивши один оберт, коло пройде шлях 2лr, точка на колі опише одну арку циклоїди (рис. 13). Відмітимо на арці точки ![]() ,
,![]() …
… ![]() , що відповідають значенням параметра t =
, що відповідають значенням параметра t = ![]() ;
; ![]() ;
; ![]() ;
; ![]() ; π, і на осі х точки
; π, і на осі х точки ![]() ,
, ![]() , ...
, ... ![]() , що відповідають тим самим значенням t. З`єднаємо ці точки відрізками
, що відповідають тим самим значенням t. З`єднаємо ці точки відрізками ![]() ,
, ![]() …
… ![]() та виміряємо кути, що вони утворюють з від'ємним напрямком осі
та виміряємо кути, що вони утворюють з від'ємним напрямком осі ![]() , використавши для цього можливості графічного редактора GeoGebra. Результати вимірювання показують: кожного разу відповідний кут дорівнює
, використавши для цього можливості графічного редактора GeoGebra. Результати вимірювання показують: кожного разу відповідний кут дорівнює ![]() . З цього випливає, що кожний із побудованих відрізків перпендикулярний до дотичної до циклоїди у відповідній точці, у тобто є нормаллю. Крім того, кожний із відрізків AB(t) = 2r
. З цього випливає, що кожний із побудованих відрізків перпендикулярний до дотичної до циклоїди у відповідній точці, у тобто є нормаллю. Крім того, кожний із відрізків AB(t) = 2r ![]() , дорівнює половині радіуса кривизни відповідної точки циклоїди (рис. 13).
, дорівнює половині радіуса кривизни відповідної точки циклоїди (рис. 13).

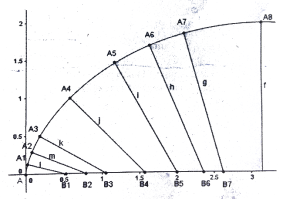 \
\
Рис. 13. Відрізки й кути під аркою циклоїди
Радіус кривизни R = 4r![]() Продовжимо кожний відрізок на його довжину. Отримаємо радіуси кривизни для відповідних значень t. З'єднавши центри кривизни плавною лінією, отримаємо еволюту циклоїди. Як бачимо з рисунку, еволютою буде циклоїда, конгрyентна даній, зсунута вниз і вліво так, як показано на рисунках 14а – в.
Продовжимо кожний відрізок на його довжину. Отримаємо радіуси кривизни для відповідних значень t. З'єднавши центри кривизни плавною лінією, отримаємо еволюту циклоїди. Як бачимо з рисунку, еволютою буде циклоїда, конгрyентна даній, зсунута вниз і вліво так, як показано на рисунках 14а – в.
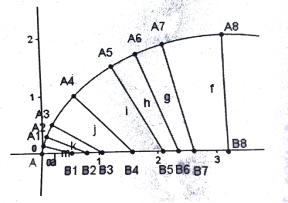
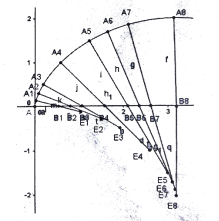
Рис. 14а Рис. 14б

Рис. 14в Еволюта циклоїди
Досліджуючи дану тему, я дізнався про історію циклоїди, її практичне застосування, провів власне дослідження з даної теми. З'ясувалося, що саме циклоїда була тим «пробним каменем», на якому Ньютон і Лейбніц випробували силу таких нових потужних методів математики, як диференціальне та інтегральне числення. В результаті вивчення властивості брахістохронності циклоїди брати Бернуллі створили новий напрямок математики - варіаційне числення.
В процесі роботи над темою я навчився будувати циклоїду за допомогою циркуля й лінійки.
Також я ознайомився з різновидами циклоїди (додаток В). Ознайомлення із задачами про циклоїду дало мені можливість вибрати напрям власних досліджень, а саме: узагальнення задач про поділ дуги в заданому відношенні.
Отримано формули для обчислення координат точки що ділить арку циклоїди в довільному відношенні m:n. Обчислено довжини дуг, що відповідають значенням параметра t =![]() /6,
/6, ![]() /4,
/4, ![]() /3, …. 2
/3, …. 2![]() . Під час систематизації результатів досліджено цікавий факт: довжини цих дуг є ірраціональними числами, що записані спряженими виразами, добуток яких - натуральне число, якщо r-натуральне. Систематизував отримані результати.
. Під час систематизації результатів досліджено цікавий факт: довжини цих дуг є ірраціональними числами, що записані спряженими виразами, добуток яких - натуральне число, якщо r-натуральне. Систематизував отримані результати.
З огляду на те, що властивості циклоїди застосовуються в технологічних розрахунках, отримані результати мають перспективу подальших досліджень.
«Дорогі не ті знання, які відкладаються в мозку, як жир; дорогі ті, які перетворюються на розумові м’язи» Г. Спенсер. Праця над науково-дослідницькою роботою допомогла мені оволодіти прийомами раціонального пошуку матеріалу, дослідити окремі прийоми розумової діяльності.
Додаток Б
Першим із учених звернув увагу на циклоїди Микола Кузанський в XV сто- літті, але серйознe дослідження цієї кривої почалося лише в XVII столітті. Назву циклоїда придумав Галілео Галілей (у Франції цю криву спочатку називали рулетmою).
Галілео ді Вінченцо Бонайуті де Галілей (італ. Galileo di Vincenzo Bonaіuti de Galilei, 15 лютого 1564 - 8 січня 1642) - італійський мислитель епохи Відродження, засновник класичної механіки, фізик, астроном, математик, поет і літературний критик, один із засновників сучасного експериментально-теоретичного природознавства. Значно вдосконалив конструкцію телескопа, а також за допомогою телескопічних спостережень довів правильність геліоцентричної теорії будови сонячної системи.
Змістовне дослідження циклоїди провів Блез Паскаль. Серед трансцендентних кривих, тобто кривих, рівняння яких не може бути записано у вигляді многочлена від х і у, циклоїда - перша з досліджуваних.
Блез Паскаль (фр. Blaise Pascal, 19 червня 1623 - 19 серпня 1662) французький філософ, письменник, фізик, математик.
Один із засновників математичного аналізу, теорії імовірності та проективної геометрії, творець перших зразків лічильної техніки, автор основного закону гідростатики. Відомий також відкриттям формули біноміальних коефіцієнтів, винаходом гідравлічного пресу й шприца та іншими відкриттями. Автор знаменитих «думок» та «Листів до провінціала», які стали класикою французької літери.
На честь Паскаля названа одиниця вимірювання тиску (паскаль), а також популярна мова програмування (Pascal).
Нова крива швидко завоювала популярність і зазнала глибокого аналізу, в якому брали участь Гюйгенс, Декарт, Ферма, Ньютон, Лейбніц, брати Бернуллі та інші корифеї науки XVII-XVIII століть. На циклоїді активно опрацьовувалися методи математичного аналізу.
Той факт, що аналітичне дослідження циклоїди виявилося настільки ж успішним, як і аналіз алгебpaїчних кривих, справив велике враження і став важливим аргументом на користь її дослідження.
XVII століття - це століття циклоїди. Кращі вчені вивчали її дивовижні властивості.

Рис. Вимірювання центральних та вписаних кутів.
Різновиди циклоїди

Рис. 1. Видовжена циклоїда

Рис. 2. Звичайна циклоїда
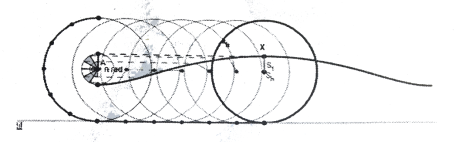
Рис. 3. Скорочена циклоїда
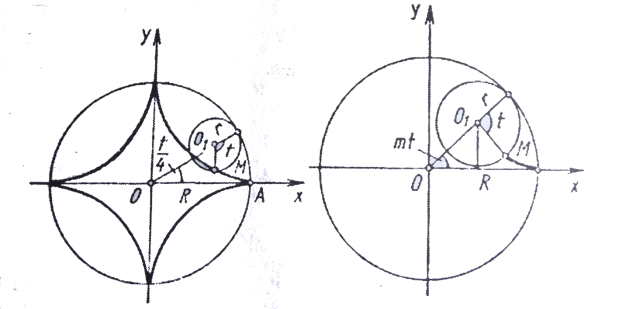
Рис. 4. Гіпоциклоїда
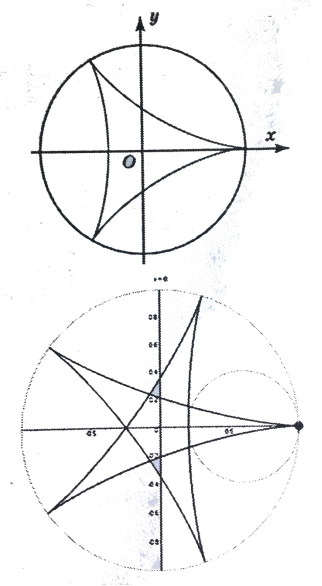
Рис. 5. Астроїда

про публікацію авторської розробки
Додати розробку
