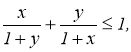Основні методи доведення нерівностей.

 

Тема: Основні методи доведення нерівностей.

Мета: освітня: систематизувати та відкоригувати вміння та навички доводити нерівності різними методами: використання означення нерівності, доведення від супротивного, використання відомої  нерівності, виділення квадрата двочлена,  застосування ключових нерівностей; перевірити та встановити рівень оволодіння учнями  способів  доведення нерівностей, вміння та навички у нестандартних ситуаціях, творчість учнів у завданнях найвищого рівня, завданнях олімпіадного характеру; повторити, глибоко осмислити навчальний матеріал з метою формування свідомого, а не формального розуміння застосування основних методів доведення нерівностей;  

 розвиваюча:  розвивати вміння лаконічно й математично грамотно висловлювати свою думку, навчати учнів правильно будувати виступи, повідомлення, критично сприймати виступи інших учнів;

виховна: виховувати працьовитість, спостережливість, кмітливість.

Тип уроку: узагальнення та систематизації знань.

Учні повинні вміти та знати: основні методи доведення нерівностей;  доводити нерівність Коші для двох невід’ємних чисел, нерівність для суми двох додатних взаємно обернених чисел,  розв’язувати вправи, у яких передбачено використання основних методів доведення нерівностей.

Хід заняття.

1. Організаційний момент

 „Ніяке людське дослідження не може бути назване істиною, якщо воно не проходить через математичні доведення”                                       Леонардо да Вінчі

II. Повідомлення теми й мети уроку, очікуваних результатів. Мотивація навчальної діяльності.

Слова вчителя. Сьогодні ми з вами перевіримо, а на якому рівні засвоїли ми тему «Доведення нерівностей». До нас звернулися за практичною допомогою учасники Всеукраїнського конкурсу «Діти за гуманне ставлення до тварин» – учні – з проханням провести розрахунки: з металу потрібно зробити каркас вольєра для безпритульних собак у формі прямокутного паралелепіпеда найбільшого об’єму за наявної кількості матеріалу загальної довжини

Для того, щоб розв’язати цю прикладну задачу, ми повинні систематизувати та відкоригувати вміння та навички доводити нерівності різними методами. Розпочинаю перехресне опитування трьох учнів, які мають високий рівень знань, з метою відновлення в пам’яті учнів тих розрізнених фактів, які будуть використовуватись на уроці. Вони утворюють так зване «зовнішнє коло»,  члени якого продуктивно працюють протягом уроку, уважно слухають відповіді учнів, не перебиваючи їх, лише піднімають сигнальну картку в разі виявлення помилки, звертають увагу на правильність думок, точність відповіді, раціональність вибору методу розв’язування, включаються в роботу, коли розв’язуємо завдання поглибленого рівня.

III. Актуалізація опорних знань

1.              Бліцопитування.

Учні дають відповіді на запитання.

Завдання для бліцопитування мають на меті перевірити навички розв’язування та доведення нерівностей. Результати опитування допоможуть далі скоригувати роботу або зупинитися для усунення прогалин у знаннях учнів.    «Вірю – не вірю».

Вчитель ставить запитання:

Чи вірите ви, що…

1. Що означає довести нерівність? (переконатися в її справедливості).
2. Які нерівності є очевидними, тобто виконуються при всіх значеннях змінних, які до них входять? (а²≥0; -а²-1<0; 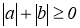; (а-b)⁴≥0.)
3. Довести, що середнє арифметичне двох  невід’ємних чисел не менше, ніж їх середнє геометричне, тобто 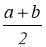≥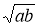, покажіть, що рівність можлива, коли а=b .
4. Дано доведення нерівності, прокоментувати кожний логічний крок його.

а²b²+ а²+ b²+4≥6аb.

 Доведення. а²b²+ а²+ b²+4-6аb= а²b²-4 аb+4+ а²-2 аb+ b² =( аb -2)² +(а-b)²≥0. ( аb -2)²≥0, (а-b)²≥0. Отже, нерівність доведена.

5. Сформулювати означення нерівності. Навести приклади.
6. Про що вам говорять прізвища видатного французького вченого Огюстена Луї Коші та видатного українського вченого Віктора Яковича Буняковського? (повідомлення учнів)

Після бліц - турніру пропонується  таблиця, що містить короткі відповіді на запропоновані питання.

2.Слова вчителя. Інформацію, яку ми повторили,  на сьогоднішньому уроці ми систематизуємо та конкретизуємо.  З’являється опорна схема:

 

 необхідно       перетворити

   

Теоретична частина

Незважаючи на результат діагностики та рівень навчальних досягнень учнів є доцільним повторити, систематизувати й узагальнити знання  та вміння із зазначеної теми.

Залежність між співвідношеннями «>», «<», «=» та значенням різниці лівої і правої частин відповідної нерівності виражає означення.

 Означення. Число а>b, якщо різниця a-b>0; число a<b, якщо різниця a-b<0;    число a=b, якщо різниця a-b=0.

          Довести нерівність – надати їй правильність при всіх допустимих значеннях змінних, що входять до неї. При доведенні нерівностей використовують властивості:

1. Властивість антирефлексивності: а>а, або а<а – хибні висловлення.

2. Властивість антисиметричності: якщо а>b, то b<а.

3. Властивість транзитивності: якщо а>b, b>c, то а>c.

 4. Властивість монотонності додавання: якщо а>b, то a+m>b+m.

  5. Властивість монотонності множення: якщо а>b, c>0, то ac>bc; >;  якщо   а>b, c<0, то аc<bc; <.

Наслідки з властивостей числових нерівностей:

1. Якщо a<b + c, то a–c<b.

2. Якщо a>0, b>0 і a<b, то >.

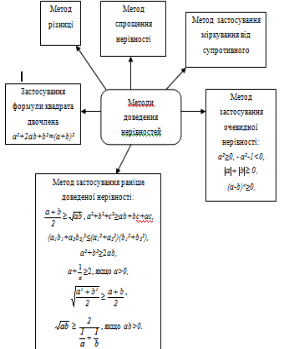Застосуємо технологію «Асоціативний кущ» – повторимо відомості про методи доведення нерівностей.

 

 

 

 

 

 

 

 

IV. Практична частина.

 Застосування знань учнів для доведення нерівностей.

1. Ігрове завдання

Захист методів доведення нерівностей	Завдання для групи: доведіть нерівність і захистіть спосіб доведення, що ви обрали	Всі застосовані методи доведення нерівностей (записує вчитель)	Колективне обговорення і розв’язання поставленого завдання
	Лідери груп жеребкуванням обирають метод доведення нерівностей для рівняння. Нерівності для захисту: а) для будь-яких дійсних  значень; б) , якщо		Взаємодія з іншими групами - складання запитань, співпраця груп під час розв’язування спільної для всього класу  задачі (у випадку, коли група не впоралася зі своїм завданням). Учні в групі доводять нерівність, обирають учня, який буде захищати метод доведення. Запис розв’язання на дошці. У ході захисту учні з інших груп ставлять запитання, шукають помилки, допущені під час доведення. Представники «зовнішнього кола» дають оцінку роботи групи

2. Розв’язування вправ для захисту.

а) для будь-яких дійсних  значень х.

Розв’язання. Перетворюватимемо ліву частину, подавши у вигляді , маємо:

= Рівність маємо лише при і х – 4 = 0 одночасно, що неможливо. Отже, остаточно , що і треба довести. 

б) , якщо  

Розв’язання. Розглянемо різницю 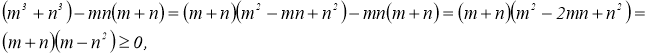  оскільки і . Тоді, що й треба довести.

1. Розв’язування олімпіадних завдань.

1. Нехай   х  та у – додатні дійсні числа. Доведіть нерівність

Розв’язання. Різниця між лівою і правою частинами дорівнює

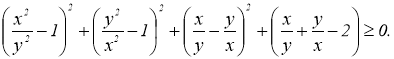
Нерівність доведена.

 2. Доведіть нерівність , де a>0, b>0, c>0, a≠b≠c.

Доведення

.

Використаємо нерівність , при a>0, b>0.

Тоді

3. Нехай і - додатні дійсні числа, для яких , .

 Доведіть, що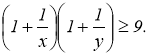     

Доведення. Оскільки , , то за нерівністю між середнім арифметичним і середнім геометричним для двох додатних чисел маємо:               

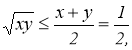, тобто тому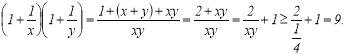

 Рівність досягається тоді і тільки тоді коли

4. Доведіть нерівність (a + 2)(b + 6)(c + 3) ≥48, якщо a≥0, b≥0, c≥0.

Доведення

Для кожного множника застосуємо теорему Коші.

, при всіх a≥0, b≥0, c≥0.

Отже, (a + 2)(b + 6)(c + 3) ≥48, якщо a≥0, b≥0, c≥0.

 

2.              Практичне застосування  методів доведення нерівностей.

Повертаємось до прикладної  задачі. У вигляді чого ми повинні змайструвати вольєри для безпритульних тварин, щоб вони мали найбільший об’єм?

Розв’язання. Позначимо довжину, ширину і висоту вольєра відповідно а, b, с. Тоді т=4 за умовою об’єм V= повинен бути найбільшим. Оскільки z, то вважаючи, що z, маємо: Тоді 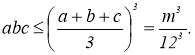   Рівність можлива, коли а=b=с. У  цьому випадку об’єм буде найбільшим. Тому вольєр повинен мати форму куба, довжину ребра якого знаходимо з рівняння  Звідки  х=

«Аукціон» доведення нерівностей. ( Кожен учень обирає  й доводить  по чотири нерівності, за що отримує відповідну кількість балів).

А)

Б) де

В) де  , ,

Г) ;

Д)

 

VI. Підбиття підсумків

 Прес-конференція. Обговорення того, наскільки продуктивною була робота по систематизації та корекції знань  та вміння доводити нерівності.

• Чи вносив вдалі пропозиції, які були враховані в ході розв’язування?
• Чи активно працював у групі?
• Чи узагальнював думки інших та просував роботу класу вперед?
• Чи змогли б ви, не володіючи методами доведення нерівності, доводити нерівності?
• Чи продуктивною була ваша робота? Що нового ви дізналися?
• Що на уроці було головним, цікавим?
• Чого ви навчилися? Чи поповнили свої знання?

 Заключні слова: «Не махай на все рукою, не лінуйся, а учись, бо чого навчишся в школі знадобиться ще колись».

 

 

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Капіносов А.М.  Основи технології навчання: Посібник, Б-ка журналу «Математика в школах України», – Харків: Видавнича група «Основа», 2006.
2. Ковтонюк  М.М. Алгебра та початки аналізу.  Б-ка журналу «Математика в  школах України».– Харків: Видавнича група  «Основа», 2006 р.
3. Маркова І.С.  Інтерактивні технології на уроках математики: Посібник.–Харків: «Основа», 2006.
4. Мерзляк А.Г., Полянський В.Б., Якір М.С. Алгебра: Підручник для класів з поглибленим вивченням математики, 9 клас – Харків, «Гімназія», 2009. 
5. Програма для класів з поглибленим вивченням математики, 8-11 класи (Уклад: Бурда М., Жалдак М. , Колесник Т., Хмара Т.,  Ядренко М. – К.: «Шкільний світ», 2001р.
6. Прокопенко Н.С., Щекань Н.П. Відкриті уроки з математики. – Харків.: Видавнича група «Основа»,  2006.