Тема: Ознака сталості функції. Достатні умови зростання  і спадання функції

Тривалість: 90 хвилин

Формування компетентностей:

• предметна компетентність: домогтися засвоєння ознаки сталості функції, достатніх умов зростання та спадання функції; сформувати вміння застосовувати ці ознаки до розв'язування задач;

ключові компетентності:

• спілкування державною мовою — міркувати, робити висновки на основі інформації, поданої в різних формах (зокрема на графіках);

• інформаційно-цифрова компетентність — діяти за алгоритмом та складати алгоритми;

• ініціативність і підприємливість — аргументувати та захищати свою позицію, дискутувати;

Обладнання: набір слайдів для повторення і вивчення нового матеріалу; мультимедійний проектор; індивідуальні карточки-завдання.

Тип заняття: засвоєння нових знань і вмінь.

Епіграф заняття:                                       

  ...Математика

безмежно різноманітна,

як світ, і присутня,

міститься в усьому.

М.П.Єругін

 

Структура :

1. Організаційна частина…………………………………………………………..….2 хв
2. Актуалізація опорних знань………………………………………………….…...19 хв
3. Сприймання і усвідомлення нового матеріалу.………………………..………..30 хв
4. Застосування знань, формування вмінь і навичок…………………………..….34 хв
5. Домашнє завдання……………………………………………………………….…2 хв
6. Підсумок заняття.…………………………………………………………………..3 хв

Хід заняття

1. Організаційна частина

Привітання. Перевірка присутності і готовності студентів до заняття: наявність форми одягу

2. Актуалізація опорних знань

Перевірка домашнього завдання

Перевірити наявність виконаних домашніх завдань та відповісти на запитання, що виникли у студентів при виконанні домашніх завдань.

             Під час догляду за хворими ви часто будете    зустрічатись з графічним завданням функції і з потребою вміти будувати ці графіки.

Температурні криві відображають різні захворювання (внутрішніх органів, інфекційні захворювання). Медичні працівники по них можуть зорієнтуватись у постановці діагнозу.

Пригадаємо правила диференціювання, якими ви користувались при розв’язуванні домашніх вправ.

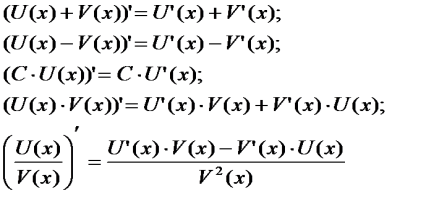
(Студенти коментують формули)

1. Знайдіть похідну функції у точці

А	Б	В	Г	Д
15	16	12	13	10

Розв’язування: обчислюємо похідну функції за табличними формулами . Далі знаходимо значення похідної в точці .

Відповідь: Г

2. Обчисліть , якщо

А	Б	В	Г	Д
0,5	-0,5	-1	1	Інша відповідь

Розв’язання: за правилами диференціювання отримаємо логарифм. Знак буде від’ємний, оскільки ще доведеться брати похідну від дужки 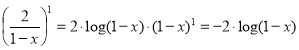. Підставимо точку у похідну

Відповідь: Д

Усне опитування

1. Знайти похідну функції ; ; ; ;; ;

2.Знайдіть неточності в даних відповідях.

а)f(х)=3х⁵-3х²+5;

Відповідь. f¹=15х⁴-5х+.

б)функція зростає на проміжку [-7;2) і (2; 8], отже функція зростає на

проміжку [-7;8] зростає.

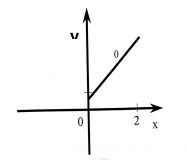
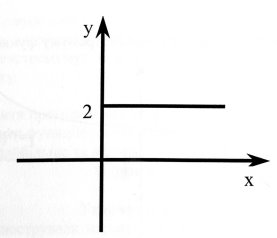
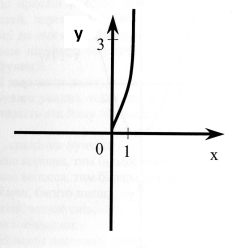
3.Тіло  рухається за законом  S(t)=t³+1. 

На якому з малюнків зображено

графік залежності швидкості від часу?

3. Сприймання і усвідомлення нового матеріалу.

Систематизація і узагальнення основних відомостей про числові функції.

Різні процеси, явища факти описуються функціями, графіки яких наочно ілюструють їх.

Вміння будувати графіки функцій і їх читати, тобто визначати проміжки      монотонності,      екстремальні      значення      і      інші характеристики     функції     за     її     графіком-важливий     елемент математичної культури.

Ці навики і вміння необхідні майбутньому інженеру, економісту і вам майбутнім медикам.

На практиці людям часто доводиться розв'язувати задачі де необхідно за допомогою найменших затрат, сил, засобів і матеріалів одержати найкращий результат. Це задачі на знаходження екстремумів функції.

Та й у природі, як сказав видатний математик XV століття Леонард Ейлер, нема нічого такого, в чому не проглядався б зміст якогось максимуму чи мінімуму.

З поняттям функції та їх властивостями деяких функцій ви вже знайомі. Згадаємо і повторимо деякі їх властивості.

• Яку функцію називають зростаючою на проміжку; спадною на проміжку?

Відповідь. Функцію називають зростаючою на деякому проміжку, якщо кожному більшому значенню аргументу з цього проміжку відповідає більше значення функції.

Функцію називають спадною на деякому проміжку, якщо кожному більшому значенню аргументу з цього проміжку відповідає менше значення функції.

• Що називають проміжком знакосталості?

Відповідь. Проміжок, на якому функція набуває значень однакового знака, називають проміжком знакосталості функції.

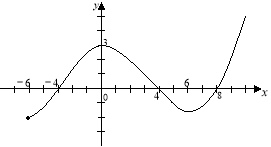
• Знайдіть за графіком нулі функції, проміжки знакосталості та монотонності, найбільше та найменше значення функції.

  Відповідь. Нулі функції: -4;4;8.

Проміжки знакосталості: (-6;-4); (-4;4); (4;8); (8;10).

Зростає на (-6;0); (6;10); спадає на (0;6).

Найбільше значення функції 5, найменше значення функції -2.

Мотивація навчання та повідомлення теми і мети заняття.

На сьогоднішньому занятті за допомогою похідної будемо визначати проміжки зростання і спадання функції.

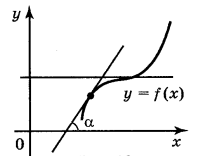Відомо, що функція y = f(x) називається зростаючою на деякому проміжку, якщо для будь-яких х₁ і х₂, що належать проміжку, із умови х₂ >  х₁ випливає, що f(x₂) > f(x₁).

Дотична в кожній точці графіка зростаючої функції, як видно з даного рисунку, утворює з додатним напрямом осі ОХ або гострий кут, або кут, що дорівнює нулю (в останньому випадку дотична паралельна осі ОХ).

Виходячи із геометричного змісту похідної: tg α = f’(x_o),

це означає, що похідна в кожній точці проміжку невід’ємна, тому для зростаючої функції f(x) виконується умова: .

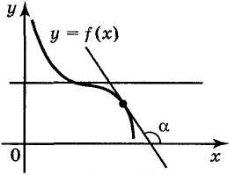Функція y = f(x) називається спадною на проміжку, якщо для будь-яких х₁ і х₂, що належать цьому проміжку, із умови х₂ >  х₁ випливає, що    f(x₂) < f(x₁). Дотична в кожній точці графіка спадної  функції (рис. 2) утворює з віссю ОХ або тупий кут, або кут, що дорів­нює

                                               нулю, тому для функції f(x), яка спадає на деякому проміжку, вико­нується умова f'(x) < О.

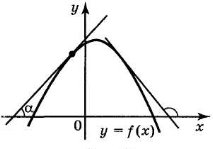На рис. 3 видно також, що одна і та ж функція може на одному про­міжку області її визначення зростати, а на іншому — спадати. Характер по­ведінки функції на кожному із цих проміжків визначається знаком її по­хідної.

Отже, наочне уявлення дозволяє спадних функцій.

Якщо функція у = f(x) диферен­ційована і зростає на деякому про­міжку, то її похідна на цьому про­міжку не від'ємна

Якщо функція у = f(x) диференційована і спадає на деякому проміжку, то її похідна на цьому проміжку не додатна.

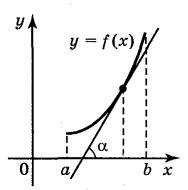Проте для розв'язування задач особливо важливими є обернені твердження, які ви­ражають ознаки зростання і спадання функ­ції на проміжку. Нехай значення похідної функції у = f(x) додатні на деякому про­міжку, тобто f'(x) > 0. Оскільки f'(x) = tg α, то із умови tg α > 0 випливає, що дотичні, проведені до графіка функції в будь-якій точці цього інтервалу, утворюють гострі кути

з додатним напря­мом осі ОХ. У цьому випадку графік

функції «піднімається»на заданому проміжку, тобтофункція зростає (рис. 4).

Якщо f'(x) < 0 на деякому проміжку, то кутовий коефіцієнт дотичної tg α = f(x) до графіка функції у = f(x) від'ємний. Це означає, що дотична до графіка функції утворює з віссю ОХ ту­пий кут і графік функції на цьому проміжку «опускається», тоб­то функція f(x) спадає (рис. 5).

Якщо f'(x) > 0 на проміжку, то функція f(x) зростає на цьому проміжку.

Якщо f(x) < 0 на проміжку, то функція f(x) спадає на цьому проміжку.

Ці два твердження називаються ознака­ми зростання (спадання) функції на про­міжку.

Проміжки зростання і спадання функції часто називають про­міжками монотонності цієї функції.

Приклад 1. Доведіть, що функція f(x) = х + зростає на проміж­ку

(1; +).

Розв'язання

Знайдемо похідну: .

Якщо х > 1, 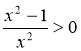то  тобто f'(x) > 0 при х > 1, і тому функція зростає на проміжку (1; +).

Знаходження проміжків зростання та спадання функції можна виконувати за таким планом:

Знайти область визначення заданої функції у = f(x).

Знайти похідну f'(x).

3. Розв'язати нерівності

а) f'(x) > 0, указати проміжки зростання функції у = f(x);

б) f'(x) < 0, указати проміжки спадання функції у = f(x)·

 

Приклад 2. Знайдіть проміжки монотонності функції у = х³ - 3х².

Розв'язання

Область визначення функції: D(y) = R.

Знаходимо похідну у' = 3х² - 6х.

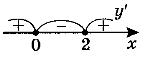
Розв'язуємо нерівності: а) у' > 0; б) у' < 0. Розв'язуємо ці не­рівності методом інтервалів, для цього знаходимо нулі по­хідної: 3х² - 6х = 0, 3х(х - 2) = 0, х = 0 або х = 2. Наносимо на координатну пряму (рис. 6) нулі похідної і ви­значаємо знаки похідної на кожному проміжку:

y'(-1) = 3 · (-1)² - 6 · (-1) = 3 + 6 = 9 > 0;

y'(1) = 3 · І² – 6 - 1 = -3 < 0;

у'(3) = 3 · 3² – 6 · 3 = 27 - 18 = 9 > 0.

а) у' > 0 в кожному із проміжків (-; 0); (2; +), отже, функція на цих  проміжках зростає.

б) у' < 0 на проміжку (0; 2), отже, функція на цьому проміжку спадає.

Відповідь: функція зростає на кожному із проміжків (-;0);(2;+); спадає на проміжку (0; 2).

3.               Застосування знань, формування вмінь і навичок

Виконання вправ:

Вправа 1

Знайдіть проміжки зростання функції

А	Б	В	Г	Д
(-3;+∞)	(-∞;-3)	(-3;3)	(3;+∞)	(-∞;3)

Розв’язання:на проміжках зростання похідна функції додатна – запам’ятайте це. Знаходимо похідну функції умови рівності нулю визначаємо точку локального екстремуму ; . В цій точці похідна функції змінює знак, зліва – від’ємна, справа додатна.  Функція зростає на інтервалі .

Відповідь: А

Вправа 2

Обчисліть , якщо кут між дотичною, проведеною до графіка функції у точці з абсцисою , і додатним напрямком осі Ox дорівнює 30⁰.

А	Б	В	Г	Д

Розв’язання: геометричний зміст похідної і точці полягає у тому, що вона рівна тангенсу кута нахилу дотичної. Знайдемо тангенс 30⁰ .

Відповідь: В

Вправа 3

До графіка функції проведено дотичну у точці з абсцисою . Обчисліть тангенс кута нахилу цієї дотичної до додатного напряму осі абсцис.

Розв’язання: Обчислимо похідну функції . Тангенс рівний похідній в точці дотику . Графік функції із дотичною наведено на рисунку

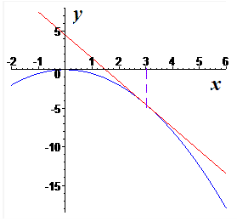
Відповідь: Б.

Вправа  3

Знайдіть стаціонарні точки функції

А	Б	В	Г	Д
1;2	-1;0	0;2	-1;2	-2;1

Розв’язання: критичні точки – це нулі похідної функції. Знайдемо похідну та прирівняємо до нуля ; ; . Знайдені критичні точки відповідають варіанту В. Графік ілюструє поведінку функції та вигляд біля знайдених точок

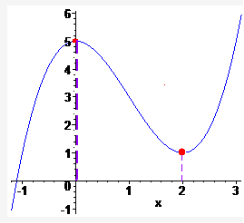
Відповідь: В

Вправа  4

Знайдіть рівняння дотичної до графіка функції у точці А(1;1).

 

А	Б	В	Г	Д
y=-2x+2	y=2x-1	y=2x+1	y=-2x-1	y=2x-2

Розв’язання: обчислимо значення похідної функції ; . Рівняння дотичної складемо за форму

. Графік дотичної до функції наведено нижче

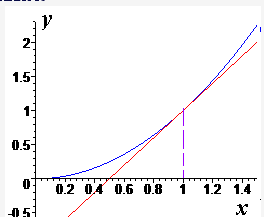
Відповідь: Б

Вправа 5

Знайдіть ординату точки на параболі , в якій кутовий коефіцієнт дотичної до параболи дорівнює 8.

А	Б	В	Г	Д
-15	-5	-1	16	15

Розв’язання: іншими словами завдання полягає в знаходженні значення функції у при якому похідна і точці рівна 8.

Обчислимо значення похідної функції та прирівнюємо його до 8. ; ; .

Визначаємо ординату для знайденого аргументу

Відповідь: А

 

 

 

 

Тести для самоконтролю

1. Функція у=f(х) визначена на множині дійсних чисел і має похідну в кожній точці області визначення. На рисунку зображено графік її похідної у=f(х). Визначте проміжки зростання функції у=f(х).

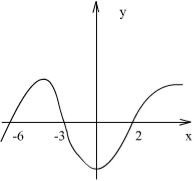
А [-3; 2]

Б визначити не можна

В (-∞;-4] і [0;  +∞ )

Г [-6;  -3] і  [2; +∞)

Відповідь: Г

2. На рисунку зображено графік  функції  у=f(х). Користуючись графіком, порівняти f'(х₃) і f'(х₆).

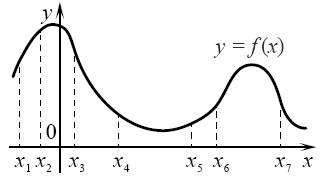
А порівняти неможливо

Б f'(х3) < f'(х6)

В f'(х3) > f'(х6)

Г f'(х3) = f'(х6)

Відповідь: Б

3. Скільки критичних точок на проміжку [х₁;х₉] має функція, графік якої зображено на рисунку?

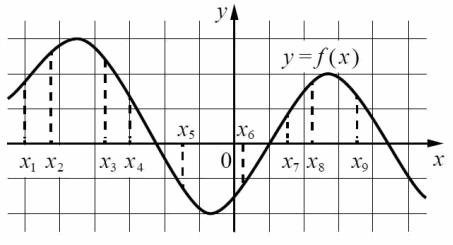
А 9

Б 8

В 7

Г 3

Відповідь: Г

4. На рисунку зображено графік похідної функції у=f(х), визначеної на проміжку [-2; 12]. Скільки проміжків спадання має функція?

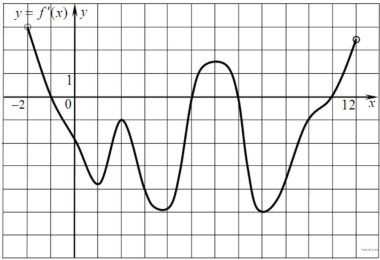
А не можна визначити

Б 2

В 1

Г 3

Відповідь: Б

5. На рисунку зображено графік  функції  у=f(х). Користуючись графіком, порівняти f'(х₇) і f'(х₈).

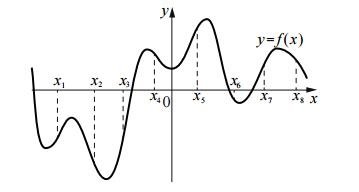
А f'(х7)  =  f'(х8)

Б  f'(х7)  > f'(х8)

В порівняти неможливо

Г f'(х7)   <  f'(х8)

Відповідь:  Б

6. Функція у=f(х) визначена на множині дійсних чисел і має похідну в кожній точці області визначення. На рисунку зображено графік її похідної у=f(х). Укажіть точки мінімуму функції у=f(х).

А 0

Б -6; -3; 2;

В -4

Г -6; 2

Відповідь: Г

7. Функція у=f(х) визначена на проміжку [-2; 12] і має похідну в кожній точці області визначення. На рисунку зображено графік її похідної у=f'(х). Скільки точок екстремуму має функція  у=f(х)?

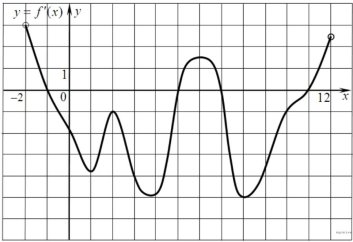
А 4 точки

Б жодної точки

В 1 точку

Г 2 точки

Відповідь: А

8. Функція у=f(х) визначена на множині дійсних чисел і має похідну в кожній точці області визначення. Скільки точок екстремуму має функція?

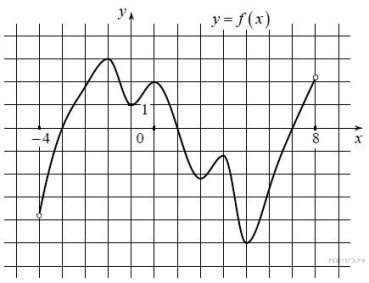
А 4

Б 3

В 6

Г 8

Відповідь: В

Аналіз правильних відповідей. Студенти відповідають з місця.

Самостійна робота

Варіант 1

1.Знайти похідну функції:

F(х)=х³-11х²+28х.

Відповідь.3х²-22х+28

2. 3найти тангенс кута нахилу дотичної до графіка

у=х³-х в точці х₀=0.

Відповідь.1

3.Знайти критичні точки функції, якщо:

F¹(х)=(х-2)(х+5)(3х+6).

Відповідь.-5;-2;2 

4.Визначте проміжки спадання функції:

f(х)=3х²-6х+7.

5.Знайти найбільше та найменше значення функції на заданому

проміжку:

f(x)=х3-3х; х є[0;2].

Відповідь.2;-2

Варіант 2

1. Знайти похідну функції,

f(х)=3х⁴-12х²+16х-1.

Відповідь.12х³-24х+16

2.Знайти тангенс кута нахилу дотичної до графіка

у=х³-х в точці x₀=0.

Відповідь. -1

3.Знайти критичні точки функції, якщо

f¹(x)=(x+1)(x-3)(2x+4)

Відповідь. -2; -1; 3.

4.Визначте проміжки зростання функції у=-3х²+24х+2.

Відповідь.(-;4)

5. Знайти найбільше та найменше значення функції на  заданому

проміжку

f(х)=3х²-х³, на[-1;3].

Відповідь.4;0

Домашнє завдання.

Г.П. Бевз, В.Г. Бевз Математика 11:К.: «Генеза», 2011.

§10 ст.78. №347, №349, №355.

Підсумок заняття.

Виставлення і мотивація оцінок.

Поглибили знання про числові функції, систематизувати навички і уміння читати властивості функції за їх графіками, знахотиди проміжки зростання і спадання функції за допомогою похідної.