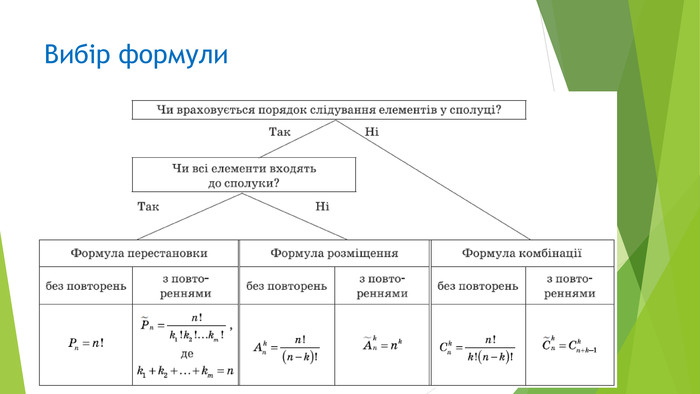
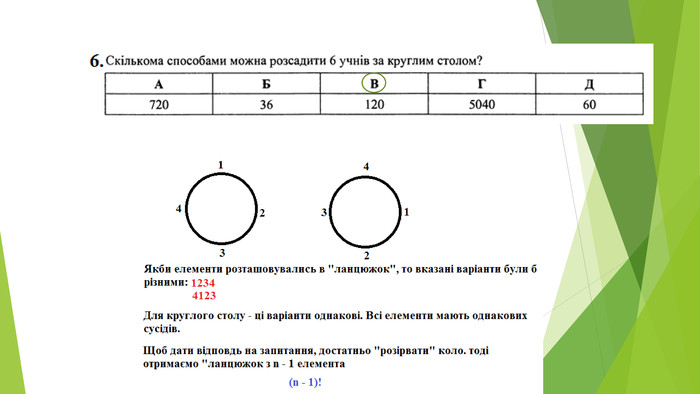
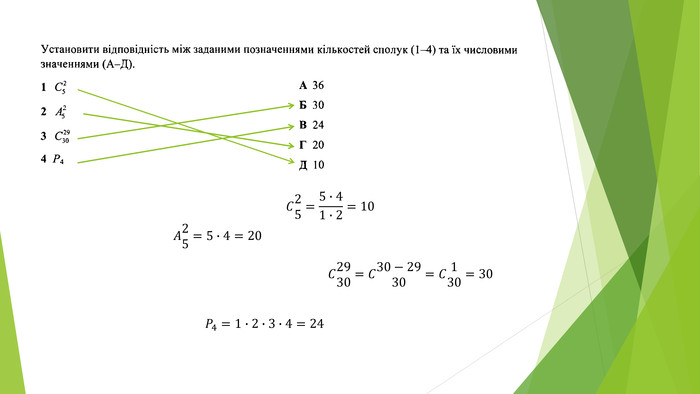
Презентація "Елементи комбінаторики"
Про матеріал
Презентація має на меті допомогти "ЗДОБУВАЧАМ ОСВІТИ" підготуватися до зовнішнього незалежного оцінювання з теми :"Комбінаторика" Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Чудовий матеріал!
-
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку