Презентація "Початки теорії ймовірностей"

Костюкевич П. П. НВК: ЗОШ №34 –економіко-правовий ліцей «Сучасник» м. КРОПИВНИЦЬКИЙПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ

За класичним визначенням ймовірність події визначається рівністю𝑝𝐴=𝑚𝑛 𝑚 – кількість елементарних подій, що сприяють події 𝐴;𝑛 – кількість всіх елементарних подій у даному експерименті. Передбачається, що всі елементарні події утворюють повну групу і рівноможливі 

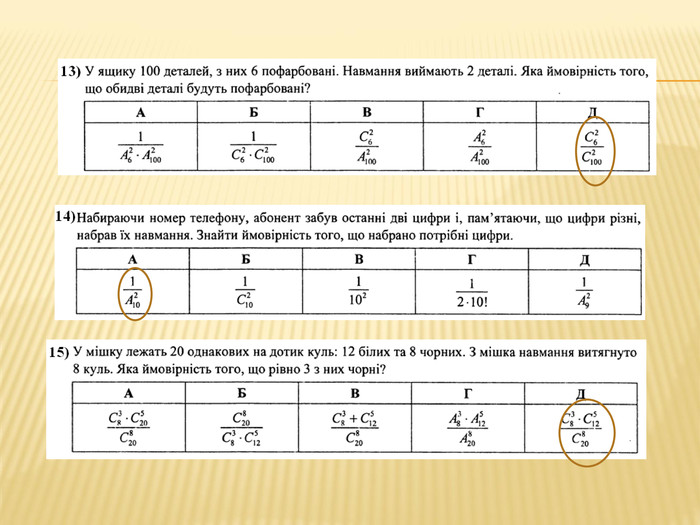
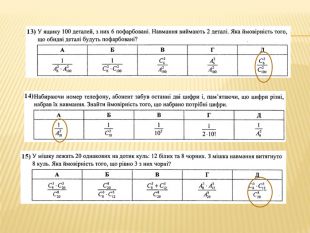
Задано цифри 1; 2; 3; 4; 5; 6. З них утворюють всі можливі шестицифрові числа, використовуючи кожну цифру тільки один раз. Знайдіть ймовірність того, що взяте навмання одне з цих чисел ділитиметься на 5. Подія А – навмання обране число ділиться на 5.𝑛=6 – загальна кількість чисел в групі𝑚=1 – одне число із групи ділиться на 5𝑝𝐴=16 

ЗНО 2006. Власник банкоматної картки забув дві останні цифри свого PIN-коду, але пам’ятає, що вони різні. Знайти ймовірність того, що з першої спроби він отримає доступ до системи. Подія А – буде отримано доступ до системи𝑚=1 – лише один варіант PIN-коду є правильним𝑛=𝐴210=10∙9=90 (кількість розміщень із 10 елементів по 2)𝑝𝐴=190 

ЗНО 2007. З натуральних чисел від 1 до 30 учень навмання називає одне. Яка ймовірність того, що це число є дільником числа 30?Подія А – обране число буде дільником числа 30. Число 𝑎 є дільником числа 𝑏 , якщо 𝑏 ділиться на 𝑎 без остачі. Важливо : 1 є дільником будь-якого натурального числа; буд-яке число є дільником самого себе .𝑛=30 – загальна кількість чисел1;2;3;5;6;10;15;30 - всі дільники числа 30, отже 𝑚=8𝑝𝐴=830=415 

Важливо. Нехай експеримент полягає в підкиданні грального кубика. Знайти ймовірності наступних подій: На верхній грані випаде 7 На верхній грані випаде число, яке не перевищує 6 Оскільки на гранях кубика немає числа 7, то 𝑚=0, тому 𝑝𝐴=06=0. Подія, ймовірність якої дорівнює 0, називається неможливою. На гранях кубика є числа 1;2;3;4;5;6. При підкиданні кубика одне з них випаде обов’язково, тому 𝑚=6. 𝑝𝐴=66=1. Подія, ймовірність якої дорівнює 1, називається вирогідною  

ЗНО 2008. У коробці є 80 цукерок, з яких 44 – з чорного шоколаду, а решта - з білого. Визначте ймовірність того, що навмання взята цукерка з коробки буде з білого шоколаду. Подія А - навмання взята цукерка з коробки буде з білого шоколаду𝑛=80 – загальна кількість цукерок𝑚=80−44=36 – кількість цукерок з білого шоколаду𝑝𝐴=𝑚𝑛=3680=920=0,45  

Пробне ЗНО 2009. У скриньці знаходяться 10 білих і 16 чорних кульок. Із скриньки навмання виймають одну кульку і відкладають. Ця кулька – білого кольору. Потім із скриньки навмання виймають ще одну кульку. Яка ймовірність того, що ця кулька буде також білою?Подія А – кулька буде білою𝑚=10−1=9 (перша кулька була білою)𝑛=16−1=15 (одну кульку забрали)𝑝𝐴=𝑚𝑛=915=35=0,6 ЗАУВАЖЕННЯ: на ЗНО правильна відповідь в тестовому завданні може бути надана або у вигляді 35 , або 0,6 

ЗНО 2011. У відділі працює певна кількість чоловіків та жінок. Навмання обрали одного зі співробітників. Ймовірність того, що це чоловік дорівнює 27 . Знайдіть відношення кількості жінок до кількості чоловіків, які працюють у цьому відділі. Подія А – обрана людина – чоловік.𝑚=2k – кількість чоловіків𝑛=7𝑘 – загальна кількість працюючих, тоді жінок 7𝑘−2𝑘=5𝑘кількість жіноккількість чоловіків=5𝑘2𝑘=2,5 

ЗНО 2013(І) . В автобусному парку налічується n автобусів, шосту частину яких було обладнано інформаційними табло. Пізніше інформаційні табло встановили ще на k автобусів з наявних у парку. Після проведеного переобладнання навмання вибирають один з n автобусів. Ймовірність того, що це буде автобус з інформаційним табло, становить 0,25. Визначте n. Уважайте, що кожен автобус обладнується лише одним табло. Подія А – обрано автобус з інормаційним табло (після переобладнання)𝑚=16𝑛+𝑘;𝑝𝐴=14⇒⇒16𝑛+𝑘𝑛=14⇒23𝑛+4𝑘=𝑛⇒𝑛=12𝑘 {5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}𝑘452𝑛486024{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}452486024

ТЕОРЕМА МНОЖЕННЯ ЙМОВІРНОСТЕЙЙмовірність спільної появи двох незалежних подій дорівнює добітку цих подій.𝑝𝐴𝐵=𝑝(𝐴)∙𝑝(𝐵)В загальному випадку: ймовірність спільної появи двох подій дорівнює добутку ймовірності однієї з них на умовну ймовірність іншої, обчисленної з припущенням того, що перша подія вже відбулася𝑝𝐴𝐵=𝑝(𝐴)∙𝑝𝐴(𝐵) 

Пробне ЗНО 2013. Студенти двох груп ( у першій – 20 студентів, у другій – 25 студентів) обирають по одному представнику з кожної групи для участі в студентському заході. Знайдіть ймовірність того, що учасниками заходу будуть обрані старости цих груп. Уважайте, що всі студенти кожної групи мають однакові шанси стати учасниками заходу, і в кожній групі є один староста. Подія А – з першої групи обрано старосту; подія В – з другої групи обрано старосту. Події А та В незалежні (вибір в першій групі не залежить від вибору в другій і навпаки)𝑝𝐴=120;𝑝𝐵=125𝑝𝐴𝐵=𝑝𝐴∙𝑝𝐵=120∙125=1500=0,002 

ЗНО 2013 (ІІ) У фестивалі беруть участь 25 гуртів, серед яких є по одному гурту з України і Чехії. Порядок виступу гуртів визначається жеребкуванням, за яким кожен із гуртів має однакові шанси отримати будь-який порядковий номер від 1 до 25. Знайдіть ймовірність того, що на цьому фестивалі гурт з України виступатиме першим, а порядковий номер виступу гурту з Чехії буде парним. Подія А – гурт з України виступатиме першим; подія В – гурт з Чехії виступатиме під парним номером (за умови, що відбулася подія А)𝑝𝐴=125; 𝑝𝐴𝐵=1224=12 (якщо подія А відбулася, то залишилось 24 порядкових номери від 2 до 25, серед яких рівно 12 – парні)𝑝𝐴𝐵=𝑝𝐴∙𝑝𝐴𝐵=125∙12=150=0,02 

ЗНО 2020 Подія А – з першої групи обрано студента, який проживає в гуртожитку; подія В – з другої групи обрано студента, який проживає в гуртожитку. Події А та В – незалежні.𝑝𝐴𝐵=𝑝𝐴∙𝑝𝐵=624∙1428=14∙12=18 Важливо: в завданнях ІІ частини відповіді ПОВИННІ бути записані десяткових дробом18=0,125 

ПРАКТИКУМ

Розв’язання завдання 9 Події «м’яч закинуто в корзину» і «промах» є протилежними (ці події несумісні і утворюють повну групу подій. «Tercia non datum» - третього не дано). Якщо 𝐴 – деяка подія, то А - протилежна подія, причому 𝑝𝐴+𝑝𝐴=1 Якщо подія А – хоча б один закине м’яч у корзину, тоді А - обидва не влучать. 𝑝𝐴=1−0,61−0,5=0,4∙0,5=0,2𝑝𝐴=1−𝑝𝐴=1−0,2=0,8 

Пояснення завдання 11 Ймовірність того, що в 𝑛 незалежних випробуваннях подія, ймовірність якої дорівнює 𝑝 , настане рівно 𝑘 разів дорівнює𝑃𝑛𝑘=𝐶𝑘𝑛∙𝑝𝑘∙(1−𝑝)𝑛−𝑘Ця формула називається формулою Бернуллі 

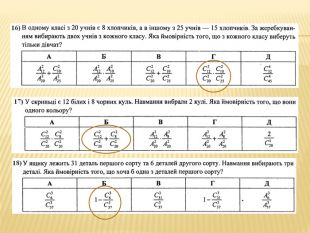
Розв’язання завдання 15 Подія А – з 8 витягнутих куль 3 чорні. Використовуємо класичне визначення ймовірності.𝑛=𝐶820 (скількома способами можна з 20 куль обрати 8, причому порядок не важливий)З 8 куль 3 повинні бути чорними, тоді 8 – 3 = 5 повинні бути білими. Будь-який вибір чорних куль відповідає довільному вибору білих, тому за правилом множення 𝑚=𝐶38∙𝐶512 

Фіолетових кульок серед перелічених немає, тому подія «вийнята кулька буде фіолетовою» неможлива.

Подія А – серед 6 деталей 4 стандартні. Використовуємо класичне визначення ймовірності: 𝑝𝐴=𝑚𝑛𝑚=𝐶47∙𝐶23;𝑛=𝐶610=𝐶410 𝑝𝐴=𝐶47∙𝐶23𝐶410  =7∙6∙5∙4∙310∙9∙8∙7=0,5 

Подія А – добуток чисел на верхній грані – парне число, тоді А - добуток – непарне число. Останнє можливо лише тоді, коли на всіх трьох верхніх гранях числа будуть непарними.𝑝𝐴=12∙12∙12=18𝑝𝐴=1−𝑝𝐴=1−18=78=0,875 

Подія А – Петрик не розв’яже задачу. 𝑝𝐴=1−0,7=0,3 Подія B – Михайлик не розв’яже задачу. 𝑝𝐵=1−0,8=0,2 Події А та В незалежні, тому 𝑝𝐴𝐵=𝑝𝐴∙𝑝𝐵=0,3∙0,2=0,06 

Подія А – влучить тільки один ( складається з двох можливостей: перший влучив, другий – ні; перший не влучив, другий влучив)𝑝𝐴=0,6∙0,1+0,4∙0,9=0,06+0,36=0,42  

Подія А – хоча б одна бракована, тоді А - обидві деталі стандартні.𝑝𝐴=1−0,051−0,04=0,95∙0,96𝑝𝐴=1−𝑝𝐴=1−0,912=0,008 

Формула повної ймовірностіЙмовірність події А, яка може настати лише при появі однієї з несумісних подій В1; В2…В𝑘 , які утворюють повну групу подій дорівнює𝑝𝐴=𝑝𝐵1∙𝑝𝐵1𝐴+𝑝𝐵2∙𝑝𝐵2𝐴+…+𝑝𝐵𝑘∙𝑝𝐵𝑘𝐴𝑝𝐵1+𝑝𝐵2+…𝑝𝐵𝑘=1 (повна група подій) 

Приклад. На завод приходять прилади з трьох заводів. 30% - з першого; 25% - з другого; 45% - з третього. Відсотки дефектних деталей становлять 7%; 10%; 12% для кожного заводу-постачальника відповідно. З партії в 1000 деталей навмання вибирають дві. Знайти ймовірність того, що рівно одна деталь буде мати дефект. За формулою повної ймовірності можемо знайти ймовірність того, що перша навмання взята деталь має дефект𝑝=0,3∙0,07+0,25∙0,1+0,45∙0,12==0,021+0,025+0,054=0,1 Отже, загальна кількість дефектних деталей 100. Подія А – з двох обраних деталей рівно одна має дефект.𝑝𝐴=2∙0,1∙0,9=0,18 (формула Бернуллі) 

Геометричні ймовірностіНехай відрізок 𝑎 є частиною відрізка 𝐿. На відрізок 𝐿 навмання поставлено точку. Ймовірність того, що ця точка потрапить на відрізок 𝑎 дорівнює𝑝=довжина 𝑎довжина 𝐿Нехай фігура 𝑔 є частиною фігури 𝐺. На фігуру 𝐺 навмання поставлено точку. Ймовірність того, що ця точка потрапить у фігуру 𝑔 дорівнює𝑝=площа 𝑔площа 𝐺 

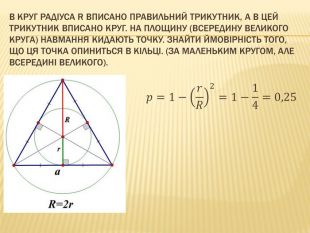
В круг радіуса R вписано квадрат, а в цей квадрат вписано круг. На площину (всередину великого круга) навмання кидають точку. Знайти ймовірність того, що ця точка опиниться в кільці. (За маленьким кругом, але всередині великого).2𝑅=2𝑎⇒𝑅=22𝑎𝑟=12𝑎𝑝=𝑆в−𝑆м𝑆в=1−𝑟𝑅2==1−122=0,5 Важливе зауваження: шукана ймовірність не залежить від радіуса

В круг радіуса R вписано правильний трикутник, а в цей трикутник вписано круг. На площину (всередину великого круга) навмання кидають точку. Знайти ймовірність того, що ця точка опиниться в кільці. (За маленьким кругом, але всередині великого).𝑝=1−𝑟𝑅2=1−14=0,25 

Узагальнення. В круг вписано правильний n-кутник, а в цей n-кутник вписано коло. Знайти ймовірність того, що точка, навмання кинута всередину великого круга, опиниться всередині кільця𝑟=𝑎2𝑡𝑔180°𝑁;𝑅=𝑎2𝑠𝑖𝑛180°𝑁 - радіуси вписаного і описаного кіл відповідно𝑝=1−𝑟𝑅2=1−𝑠𝑖𝑛180°𝑁𝑡𝑔180°𝑁2= =1−𝑐𝑜𝑠2180°𝑁=𝑠𝑖𝑛2180°𝑁  

Двоє закоханих домовились про зустріч в певному міСці між 20.00 та 21.00. Якщо хтось приходить і не знаходить свого обранця, то чекає 20 хвилин і потім йде. Знайти ймовірність того, що зустріч відбудеться. В прямокутній декартовій системі координат розглянемо квадрат зі стороною 60. Нехай х (в хвилинах) час приходу на зустріч першого закоханого (0≤𝑥≤60), y – час приходу іншого (0≤𝑦≤60). Умова, за якої відбудеться зустріч, описується нерівністю: 𝑦−𝑥≤20 Графічно ця умова зображена на малюнку. Шукана ймовірність: 𝑝=60∙60−40∙403600=1−49=59