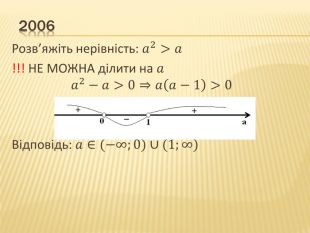
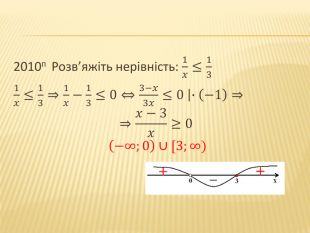
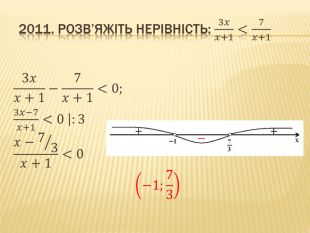
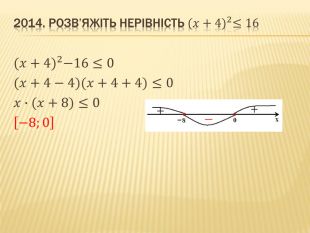
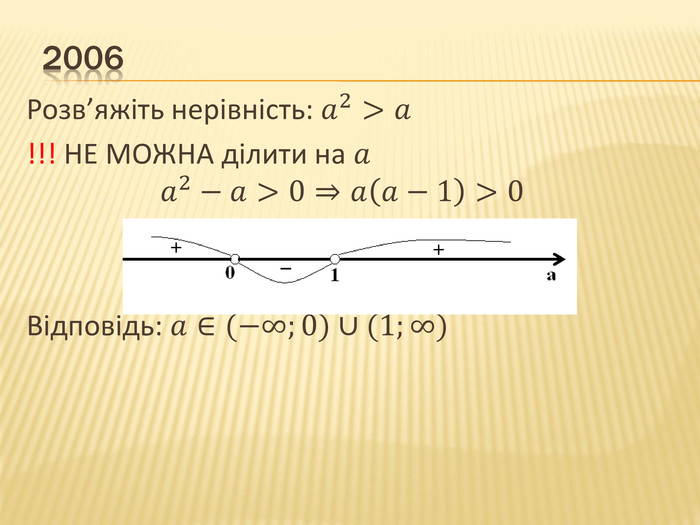
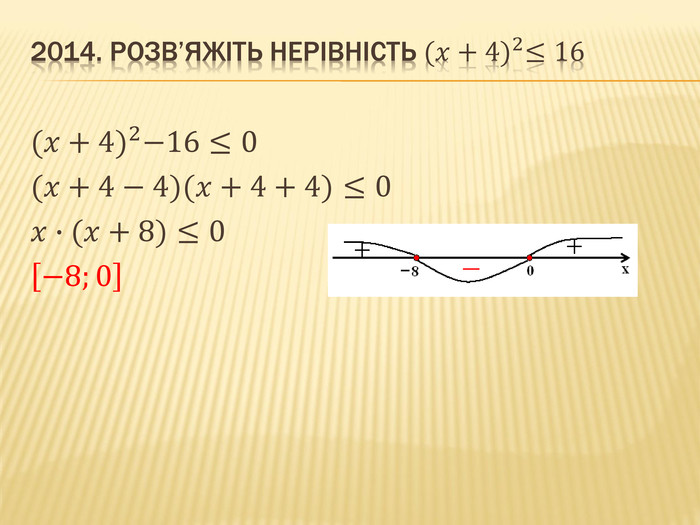
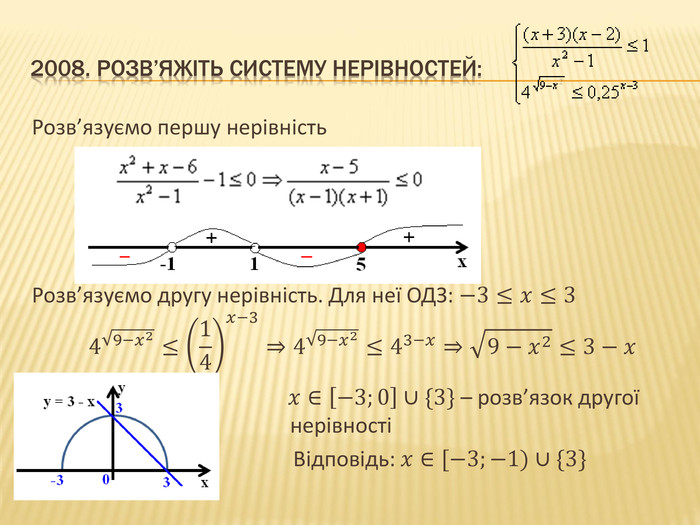
Презентація "Нірівності"

![При діленні (множенні) нерівності на від’ємне число – ВСІ знаки змінюються на протилежніЯкщо нерівність сторога (< або >), то для запису відповіді використовуємо «круглі» дужки «)» або «(«. Якщо нерівність нестрога (≤ або ≥), то для запису відповіді використовуємо «квадратні» дужки «[« або «]» При діленні (множенні) нерівності на від’ємне число – ВСІ знаки змінюються на протилежніЯкщо нерівність сторога (< або >), то для запису відповіді використовуємо «круглі» дужки «)» або «(«. Якщо нерівність нестрога (≤ або ≥), то для запису відповіді використовуємо «квадратні» дужки «[« або «]»](/uploads/files/334031/217385/233378_images/2.jpg)

![ЗНО 2015 Розв’яжіть неівність: 0,2𝑥−54<00,2𝑥<54 :0,2 𝑥<270(−∞;270) Розв’яжіть нерівність: (𝑥−6)(𝑥+2)2𝑥−3≤0 {−2}∪(3;6] ЗНО 2015 Розв’яжіть неівність: 0,2𝑥−54<00,2𝑥<54 :0,2 𝑥<270(−∞;270) Розв’яжіть нерівність: (𝑥−6)(𝑥+2)2𝑥−3≤0 {−2}∪(3;6]](/uploads/files/334031/217385/233378_images/4.jpg)
![2016. Укажіть число, що є розв’язком нерівності 5𝑥−3≥1−2 0 2 9 4 5𝑥−3≥1⇔5𝑥−3−1≥0⇔5−(𝑥−3)𝑥−3≥0⇔ ⇔8−𝑥𝑥−3≥0 ∙−1 𝑥−8𝑥−3≤0 𝑥∈(3;8] З наведених чисел знайденій множині належить лише число 4 2016. Укажіть число, що є розв’язком нерівності 5𝑥−3≥1−2 0 2 9 4 5𝑥−3≥1⇔5𝑥−3−1≥0⇔5−(𝑥−3)𝑥−3≥0⇔ ⇔8−𝑥𝑥−3≥0 ∙−1 𝑥−8𝑥−3≤0 𝑥∈(3;8] З наведених чисел знайденій множині належить лише число 4](/uploads/files/334031/217385/233378_images/5.jpg)






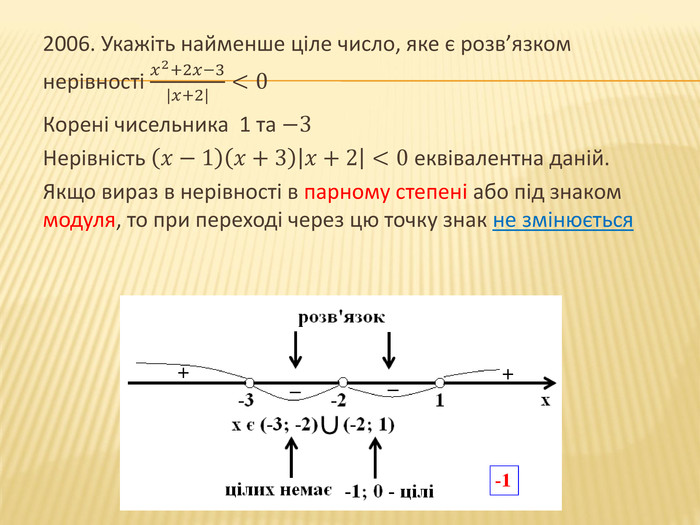

![2009. Знайдіть КІЛЬКІСТЬ усіх цілих розв’язків нерівності 𝑥2−𝑥−12(𝑥+1)2≤0. Якщо нерівність має безліч цілих розв’язків, то у відповідь запишіть число 100.𝑥2−𝑥−12=0; 𝐷=(−1)2−4∙1∙−12=49𝑥1=1−72=−3;𝑥2=1=72=4(𝑥+3)(𝑥−4)(𝑥+1)2≤0 𝑥∈−3;−1∪(−1;4] Цілі числа: −3;−2;0;1;2;3;4 Кількість: 7 2009. Знайдіть КІЛЬКІСТЬ усіх цілих розв’язків нерівності 𝑥2−𝑥−12(𝑥+1)2≤0. Якщо нерівність має безліч цілих розв’язків, то у відповідь запишіть число 100.𝑥2−𝑥−12=0; 𝐷=(−1)2−4∙1∙−12=49𝑥1=1−72=−3;𝑥2=1=72=4(𝑥+3)(𝑥−4)(𝑥+1)2≤0 𝑥∈−3;−1∪(−1;4] Цілі числа: −3;−2;0;1;2;3;4 Кількість: 7](/uploads/files/334031/217385/233378_images/16.jpg)
![2013. Розв’яжіть нерівність 4𝑥+3+6𝑥≥1. У відповідь запишіть суму цілих розв’язків. 4𝑥+6(𝑥+3)𝑥(𝑥+3)−1≥04𝑥+6𝑥+18−𝑥2−3𝑥𝑥(𝑥+3)≥0−𝑥2+7𝑥+18𝑥(𝑥+3)≥0 ∙(−1) 𝑥2−7𝑥−18𝑥(𝑥+3)≤0 𝑥2−7𝑥−18=0𝐷=49−4∙−18=121𝑥1=7−112=−2𝑥2=7+112=9(𝑥+2)(𝑥−9)𝑥(𝑥+3)≤0 𝑥∈(−3;−2]∪(0;9]1+92∙9−2=43 43 2013. Розв’яжіть нерівність 4𝑥+3+6𝑥≥1. У відповідь запишіть суму цілих розв’язків. 4𝑥+6(𝑥+3)𝑥(𝑥+3)−1≥04𝑥+6𝑥+18−𝑥2−3𝑥𝑥(𝑥+3)≥0−𝑥2+7𝑥+18𝑥(𝑥+3)≥0 ∙(−1) 𝑥2−7𝑥−18𝑥(𝑥+3)≤0 𝑥2−7𝑥−18=0𝐷=49−4∙−18=121𝑥1=7−112=−2𝑥2=7+112=9(𝑥+2)(𝑥−9)𝑥(𝑥+3)≤0 𝑥∈(−3;−2]∪(0;9]1+92∙9−2=43 43](/uploads/files/334031/217385/233378_images/17.jpg)





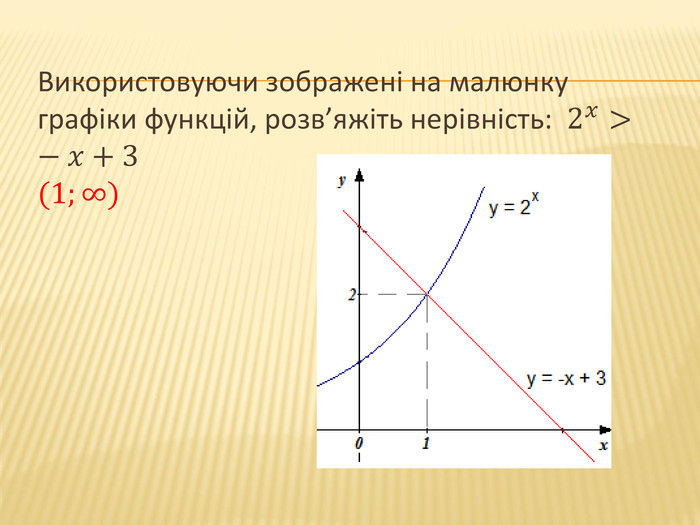

![2013. Розв’яжіть нерівність: 2𝑥≤3 Основна логарифмічна тотожність: 𝑎𝑙𝑜𝑔𝑎𝑏=𝑏2𝑥≤2𝑙𝑜𝑔23 (−∞; 𝑙𝑜𝑔23] 2013. Розв’яжіть нерівність: 2𝑥≤3 Основна логарифмічна тотожність: 𝑎𝑙𝑜𝑔𝑎𝑏=𝑏2𝑥≤2𝑙𝑜𝑔23 (−∞; 𝑙𝑜𝑔23]](/uploads/files/334031/217385/233378_images/26.jpg)


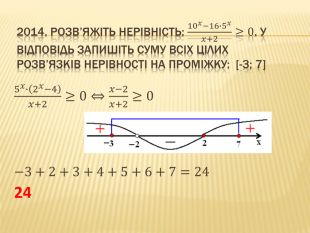
![2014. Розв’яжіть нерівність: 10𝑥−16∙5𝑥𝑥+2≥0. У відповідь запишіть суму всіх цілих розв’язків нерівності на проміжку: [-3; 7] 5𝑥∙2𝑥−4𝑥+2≥0⇔𝑥−2𝑥+2≥0 −3+2+3+4+5+6+7=24 24 2014. Розв’яжіть нерівність: 10𝑥−16∙5𝑥𝑥+2≥0. У відповідь запишіть суму всіх цілих розв’язків нерівності на проміжку: [-3; 7] 5𝑥∙2𝑥−4𝑥+2≥0⇔𝑥−2𝑥+2≥0 −3+2+3+4+5+6+7=24 24](/uploads/files/334031/217385/233378_images/29.jpg)





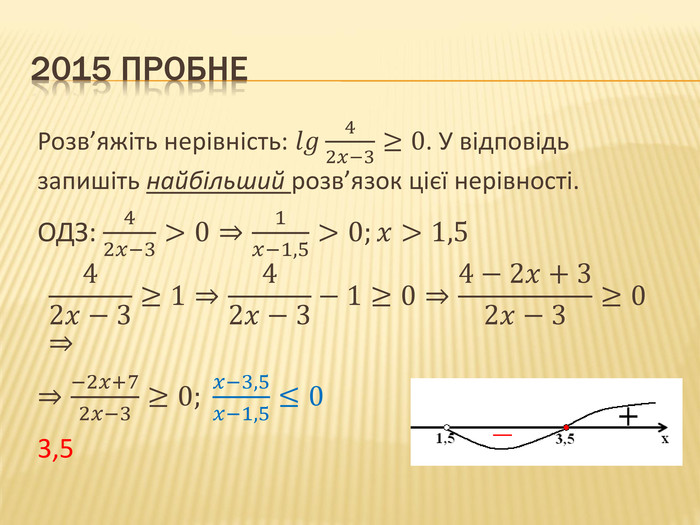
![2013. Розв’яжіть нерівність: 𝑙𝑜𝑔0,4𝑥≥𝑙𝑜𝑔0,42 ОДЗ: 𝑥>0𝑥≤2 (0;2] 2016. Розв’яжіть нерівність: log3𝑥<−1 ОДЗ: 𝑥>0𝑥>3−1;𝑥>13 13;∞ 2013. Розв’яжіть нерівність: 𝑙𝑜𝑔0,4𝑥≥𝑙𝑜𝑔0,42 ОДЗ: 𝑥>0𝑥≤2 (0;2] 2016. Розв’яжіть нерівність: log3𝑥<−1 ОДЗ: 𝑥>0𝑥>3−1;𝑥>13 13;∞](/uploads/files/334031/217385/233378_images/35.jpg)


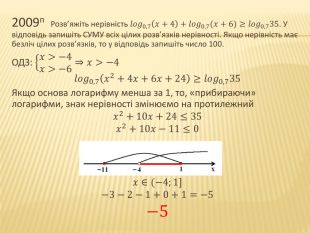
![2009п Розв’яжіть нерівність 𝑙𝑜𝑔0,7𝑥+4+𝑙𝑜𝑔0,7(𝑥+6)≥𝑙𝑜𝑔0,735. У відповідь запишіть СУМУ всіх цілих розв’язків нерівності. Якщо нерівність має безліч цілих розв’язків, то у відповідь запишіть число 100. ОДЗ: 𝑥>−4𝑥>−6⇒𝑥>−4 𝑙𝑜𝑔0,7𝑥2+4𝑥+6𝑥+24≥𝑙𝑜𝑔0,735 Якщо основа логарифму менша за 1, то, «прибираючи» логарифми, знак нерівності змінюємо на протилежний𝑥2+10𝑥+24≤35𝑥2+10𝑥−11≤0𝑥∈(−4;1]−3−2−1+0+1=−5−5 2009п Розв’яжіть нерівність 𝑙𝑜𝑔0,7𝑥+4+𝑙𝑜𝑔0,7(𝑥+6)≥𝑙𝑜𝑔0,735. У відповідь запишіть СУМУ всіх цілих розв’язків нерівності. Якщо нерівність має безліч цілих розв’язків, то у відповідь запишіть число 100. ОДЗ: 𝑥>−4𝑥>−6⇒𝑥>−4 𝑙𝑜𝑔0,7𝑥2+4𝑥+6𝑥+24≥𝑙𝑜𝑔0,735 Якщо основа логарифму менша за 1, то, «прибираючи» логарифми, знак нерівності змінюємо на протилежний𝑥2+10𝑥+24≤35𝑥2+10𝑥−11≤0𝑥∈(−4;1]−3−2−1+0+1=−5−5](/uploads/files/334031/217385/233378_images/38.jpg)


При діленні (множенні) нерівності на від’ємне число – ВСІ знаки змінюються на протилежніЯкщо нерівність сторога (< або >), то для запису відповіді використовуємо «круглі» дужки «)» або «(«. Якщо нерівність нестрога (≤ або ≥), то для запису відповіді використовуємо «квадратні» дужки «[« або «]»
Знайти кількість цілих розв’язків (7−3𝑥)3∙2𝑥−115∙(15−𝑥)101(6−𝑥)2019∙(13𝑥−172)2018≥0 Наступна нерівність еквівалентна даній𝑥−73∙𝑥−5,5∙(𝑥−15)(𝑥−6)∙(𝑥−14)2≤0 Вирази 𝑥−𝑎 та (𝑥−𝑎)𝑛 однаково впливають на зміну знака нерівності. Вирази 𝑎𝑥−𝑏 та 𝑥−𝑏𝑎 еквівалентні щодо знаку нерівності.𝑥∈213;5,5∪(6;14)∪14;15𝑥∈3;4;5;7;8;9;10;11;12;13;15 11
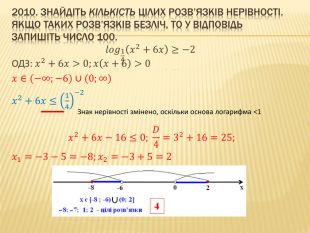
2010. Розв’яжіть нерівність 12𝑥2−𝑥>8𝑥−5. У відповідь запишіть суму всіх цілих розв’язків цієї нерівності. Якщо нерівність має безліч цілих розв’язків, то у відповідь запишіть число 100. 2−1𝑥2−𝑥>23𝑥−52−𝑥2+𝑥>23𝑥−15 (основа >1. Знак нерівності не міняємо)−𝑥2+𝑥>3𝑥−15;−𝑥2−2𝑥+15>0 ∙(−1)𝑥2+2𝑥−15<0 – розв’язок «між коренями» відповідного квадратного рівняння. 𝐷4=1+15=16; 𝑥1=−1−4=−5; 𝑥2=−1+4=3 𝑥∈(−5;3)ЦІЛІ розв’язки: −4;−3;−2;−1;0;1;2 Сума: −7
2011п Розв’яжіть нерівність: 3∙9𝑥−2∙15𝑥−52𝑥+1>0. Якщо нерівність має цілі розв’язки, то вкажіть найбільший з них. Якщо нерівність має цілі розв’язки, але вказати найбільший неможливо, то у відповідь запишіть число 50. Якщо нерівність не має цілих розв’язків, то у відповідь запишіть число 100.3∙32𝑥−2∙3𝑥∙5𝑥−5∙52𝑥>0 : 32𝑥>0−5∙532𝑥−2∙53𝑥+3>0 ∙(−1) 5∙532𝑥+2∙53𝑥−3<0 – нерівність квадратна відносно 53𝑥. Її розв’язки – «між коренями» відповідного квадратного рівняння: 5𝑡2+2𝑡−3=0; 𝐷4=1−5∙−3=16 𝑡1=−1−45=−1;𝑡2=−1+45=35⇒−1<53𝑥<35⇒𝑥<−1 Відповідь: -2
2009п Розв’яжіть нерівність 𝑙𝑜𝑔0,7𝑥+4+𝑙𝑜𝑔0,7(𝑥+6)≥𝑙𝑜𝑔0,735. У відповідь запишіть СУМУ всіх цілих розв’язків нерівності. Якщо нерівність має безліч цілих розв’язків, то у відповідь запишіть число 100. ОДЗ: 𝑥>−4𝑥>−6⇒𝑥>−4 𝑙𝑜𝑔0,7𝑥2+4𝑥+6𝑥+24≥𝑙𝑜𝑔0,735 Якщо основа логарифму менша за 1, то, «прибираючи» логарифми, знак нерівності змінюємо на протилежний𝑥2+10𝑥+24≤35𝑥2+10𝑥−11≤0𝑥∈(−4;1]−3−2−1+0+1=−5−5


про публікацію авторської розробки
Додати розробку