Паралельність прямих і площин у просторі

Тема: Формування та розвиток критичного мислення під час розв`язування задач з теми: «Паралельність прямих і площин у просторі».

Мета: Узагальнити знання учнів з теми, вдосконалювати  навички застосування теоретичного матеріалу до розв’язування задач, відпрацювати норми співробітництва під час групової діяльності та почуття взаємодопомоги, взаєморозуміння, розвивати творчі здібності і пізнавальний інтерес з урахуванням індивідуальних особливостей учнів.

 Тип заняття : закріплення основних знань, формування вмінь і навичок.

 Обладнання:

                                               Хід заняття:

1. Мотиваційна бесіда з подальшою постановкою цілей.

Геометрія – це цілий світ, який оточує нас з самого народження, бо все, що ми бачимо навколо себе, так чи інакше, має відношення до геометрії.

Епіграф:  «Природа і життя людини формулює власні закони мовою математики.»                                             Г.Галілей

Девіз уроку:   «Дивись – думай - роби висновки!»

2. Перевірка домашнього завдання

Домашнє завдання перевіряється двома лініями одночасно.

Двом слабшим учням роздаються картки де розв’язують одну домашню задачу.

Іншу задачу проектують на екран. Допущено помилку.

3. Повідомлення теми та мети заняття.

4. Представлення творчого домашнього завдання.

Учні готували презентації по теоретичному матеріалу.

5.Матаматичний диктант.

Дано зображення куба: варіант 1 — рис. 53, варіант 2 — рис. 54.

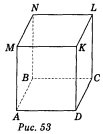
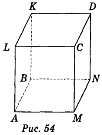
Користуючись зображенням, запишіть:

1. пряму, яка паралельна площині ВСМ і проходить через точку D;
2. грані куба, які паралельні прямій СD;
3. площину, яка містить пряму ВN і паралельна прямій СD;
4. площину, яка паралельна прямій СD і проходить через точку К;
5. площини, які паралельні прямій ВМ;
6. прямі, паралельні площині АВМ.

Учні здійснюють самоперевірку і виставляють оцінки.

Відповідь. Варіант 1.1) АD; 2) АВNМ і МNLК; 3) АВN; 4) КМN і АВК; 5) DСК, LСА, КDM; 6) КL, LС, СD, КD, КС, DL.

  Варіант 2.1) DN; 2) АВКL, АВNМ; 3) АВN; 4) АВК і КLМ; 5) СDК, КCN, КСА; 6) KL, LС, СD, KD, KС, DL.

6. Представлення творчого домашнього завдання (2).

Презентація про основні типи задач з даної теми ,способи їх розв’язання.

7. Розвязування задач.

На доведення задачі пропонують студенти в презентації .

На розвзання задачу підбирає  викладач.

Через кінець К відрізка проведено площину. Через кінець D  і точку Р цього відрізка проведено паралельні прямі, які перетинають площину в точках Р1 і D1. Знайдіть довжину відрізка КD, якшо КР = 2N см, DD1=3N см,РР1 = Nсм.

( N- порядковий номер студента в журналі)

Відповідь - 6Nсм.

8. Робота в групах.

Учні об’єднуються в 3 групи. Розв’язують завдання подібної контрольної роботи. Капітан виставляє всім оцінки. Один студент, за жеребкуванням, здає зошит для перевірки. Так підтверджує, або спростовує оцінки всієї команди.

Завдання для роботи в групах

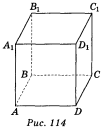
1. Користуючись зображенням куба ABCDA₁B₁C₁D₁ (рис. 114), запишіть грані куба, які паралельні ребру AA₁.
2.  Знайдіть площу круга описаного навколо трикутника зі сторонами 18 см, 24 см і 30 см.
3. Прямі а і b перетинаються, пряма с перетинає пряму а і паралельна прямій b. Доведіть, що прямі а, b, с лежать в одній площині.
4. Дві сторони даного трикутника паралельні площині α. Доведіть, що і третя його сторона паралельна цій площині.
5. Площина α перетинає сторони АВ і ВС трикутника АВС в точ­ках М і N відповідно і паралельна стороні АС. Знайти довжину від­різка MN, якщо АС = 24 см, а ВМ:АМ = 3:1.

9. Підсумок завдання.

Перегляд слайдів геометрія навколо нас.

Виставлення оцінок вчителю.

(на стікерах і кладуть в скриньку)

10.  Домашнє завдання.

1група - варіант домашньої контрольної роботи.

2 група - підготувати завдання на контрольну роботу по даній темі.